飞轮储能风力发电系统的功率快速平滑控制策略研究

(国电南瑞科技股份有限公司，江苏 南京 210061)

0 引 言

风能具有随机性、间歇性等特点，风力发电系统直接并网易导致网侧电压与频率的波动、畸变，于电网的安全运行不利，甚至可能造成电网崩溃[1—2]。储能装置可平滑风力发电机组的输出功率，有利于电网安全运行，提高电网对风电的接纳能力[3—4]。飞轮储能装置为机械储能装置，具有对环境友好、效率高、充放电深度可控、可深度充放电等优点，使得其在风力发电系统中具有一定的竞争力[5—7]。

但是飞轮储能系统的并网逆变器输出功率的高频扰动将降低电网吸纳风能的能力。为此，提出了能实现快速功率平滑控制、减少并网功率波动、增加电网吸纳能力的功率快速平滑控制策略。所提出的飞轮储能风力发电系统控制策略中包含了风力发电系统的控制策略、飞轮储能系统控制策略以及并网逆变器的控制策略。

1)风力发电系统的控制策略采用文献[8]介绍的最大功率点跟踪控制(maximum power point tracking，MPPT)。该文献针对直驱式永磁同步风力发电系统存在的非线性、不确定性、强干扰的问题，提出一种很好的基于滑模自适应控制算法的最大功率点跟踪策略。

2) 飞轮储能系统与并网逆变器控制则采用滞环控制[9—10]与三角载波相结合的定频滞环控制策略。

虽然滞环控制策略结构简单、调节速度快、易实现、响应速度快、鲁棒性好且不存在平均跟踪误差[11—12]，然而其开关频率不固定，致使其输出电流谐波大，输出滤波器设计尺寸较大。文献[13]提出了一种定时滞环比较器，但是该方法存在平均跟踪误差，导致系统的稳定精度变差。文献[14]则通过调节系统参数动态调整滞环阈值，但存在跟踪失步的可能。

针对以上不足，提出采用三角载波与滞环控制策略相结合的方法，即将电流误差叠加上三角载波，实现开关频率固定的定频滞环控制策略。而对于并网逆变器的控制则采用瞬时功率理论直接计算交直轴电流的参考值，减少了PI控制器；而采用定频滞环控制策略，则不需要对电网电压进行锁相，进一步降低了控制系统的软件成本。

3)飞轮储能控制系统的充放电功率参考值可通过并网功率的波动获得。

文献[15]通过测量风速的平均值，设置飞轮储能系统的充放电功率参考值；然而风速波动大，测量误差大，导致储能系统的平滑效果不理想。而文献[11]则将风力发电系统的最大输出功率与平均输出功率的平均值作为储能系统充放电功率的参考值，采用该方法容易导致储能系统长时间充电或放电；然而储能系统的存储容量有限，储能系统过渡放电或充满电后，将失去平滑功率的功能，因此该方法适用于储能容量较大的场合。

由于飞轮储能系统的充放电功率是为了平滑风力发电系统的并网功率，因此提出通过检测并网逆变器的输出功率，将其作为飞轮储能系统的充放电功率参考值。而对于并网逆变器而言，其输出功率的高频波动即是风能的随机性、波动性导致的电网侧并网功率波动。因此，提出采用并网逆变器输出功率的高通滤波分量作为飞轮储能系统的输出功率参考值。

下面基于所提出的控制策略，搭建了飞轮储能风力发电系统模型，并进行仿真分析和实验验证。结果表明：所采用的并网逆变器输出功率滤波算法确定储能系统的充放电参考值具有不增加系统硬件成本、误差小、抑制网侧波动能力高等优点，同时采用定频滞环控制策略控制系统的软件成本得到了降低。

1 风力发电系统结构

图1为飞轮储能异步电机风力发电系统的结构框图，图中：电机为直驱鼠笼条式异步电机，具有成本低、结构可靠坚固、鲁棒性高等特点；飞轮储能系统中的电动/发电机也采用异步电机；并网逆变器、风力发电机侧变换器与飞轮储能系统侧变换器均采用三相脉冲宽度调制(pulse width modulation，PWM)变换器。

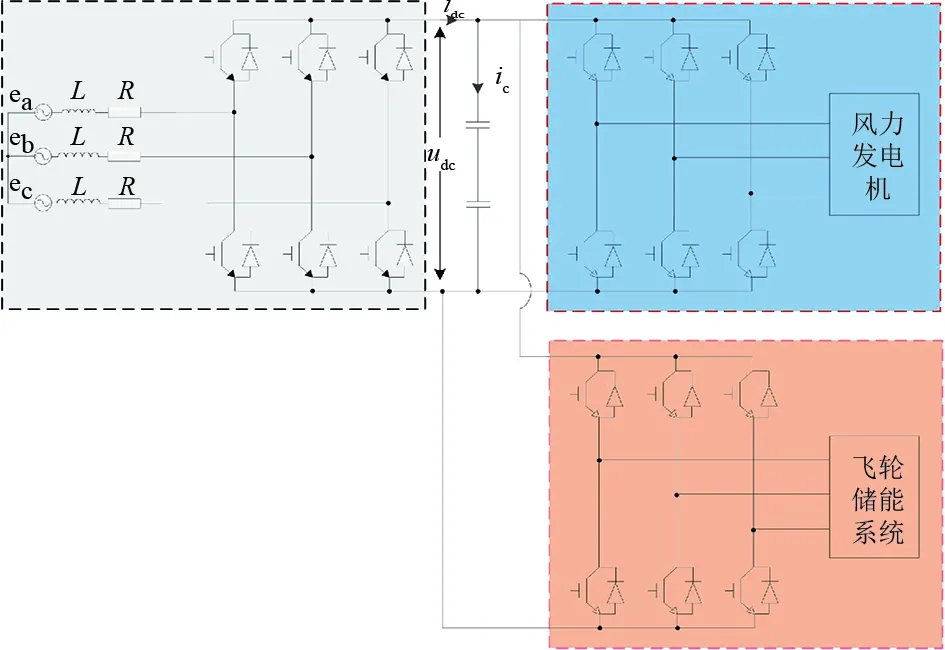
图1 风力发电系统结构

2 飞轮储能风力发电系统控制策略

2.1 风力发电机组的控制策略

风力发电机的风能利用系数Cp(λ)是叶尖速度比λ的函数，图2为某一固定风速下的Cp(λ)与λ的关系图。图中，Cp-max即为最大功率点追踪控制的最大输出功率点。可通过控制风力发电机的转速调节叶片角速度，实现风力发电系统的最大功率点追踪。此时，风力发电机的转矩参考值Te-ref可利用Cp-max描述，如式(1)所示。

图2 风能利用系数特性

(1)

式中：ρ为空气密度,kg/m3；R为叶片半径；λopt为最佳叶尖速比；ωt为风机风轮角速度。

即式(1)可根据风速、风能利用系数计算最大功率点处风力发电机的转矩，作为风力发电机控制的转矩参考值。笼型异步风力发电机在转子磁场定向的两相旋转坐标系下的数学模型可参考文献[16]，其风力发电机的控制策略框图如图3所示。

图3 风力发电机控制框图

2.2 并网逆变器控制策略

图1中并网逆变器的输入有功功率Pg-ref可表示为

Pg-ref=Udc(idc-ic)

(2)

式中:Udc为直流母线电压；idc为并网逆变器输出电流；ic为流进直流母线电容的电流。ic可通过直流母线电压的控制器获得，即可表示为

ic=P/(Udc-ref-Udc)

(3)

式中,Udc-ref为直流母线电压参考值。

两相旋转dq坐标系下，由瞬时功率理论可知：

(4)

(5)

式中：Pg-ref、Qg-ref分别为并网逆变器输入的有功功率和无功功率；Ed、Eq分别为网侧三相电压在dq坐标系下的d轴分量与q轴分量；id-ref、iq-ref分别为直轴电流参考值和交轴电流参考值。

将式(4)两端同时乘以Ed，式(5)两端同时乘以Eq，可将id-ref表示为

(6)

将式(4)两端同时乘以Eq，式(5)两端同时乘以Ed，可将iq-ref表示为

(7)

根据式(6)、式(7)可直接计算并网逆变器的直轴电流参考值和交轴电流参考值，而文献[17]采用的PI控制器计算交直轴电流，存在参数调节不准确等问题。

采用所提的瞬时功率理论与定频滞环控制策略时，并网逆变器的控制策略框图如图4所示。该策略无需锁相环进行锁相，提高了系统控制效率与可靠性。

2.3 飞轮储能系统控制策略

图1中，飞轮储能系统通过三相PWM变换器直接与直流母线相连，以维持直流母线电压恒定。

飞轮储能系统中存储的动能可表示为

(8)

式中：Ef-ref为当前时刻，飞轮储能系统存储的能量；Ef1为飞轮储能系统存储能量的初始值；Pref为电动/发电机的输入功率参考值。

图4 并网逆变器控制框图

采用低通滤波器与高通滤波器两类滤波器获取飞轮储能装置的功率输入参考值，其中高通滤波器输出的有功功率参考值为风力发电系统输出功率的波动分量，通过该有功功率的扰动成分，可有效抑制风力风电发电系统对电网的影响。

即飞轮储能系统的功率参考值Pref可由网侧输出功率经过高通滤波后获得，如图5所示。

图5 飞轮储能系统功率参考值

由动能公式可知，此时电动/发电机的机械转速参考值可表示为

(9)

式中，J为飞轮转子的转动惯量。

图6中，磁链估算可通过式(10)实现，转矩估算可通过式(11)实现。

图6 飞轮储能系统控制框图

(10)

Te-f=np-f(Ψf-sdif-sq-Ψf-sqif-sd)

(11)

式中：Ψf-s、Ψf-sd、Ψf-sq分别为定子磁链、定子磁链d轴分量、定子磁链q轴分量；uf-sd、uf-sq分别为飞轮电机的定子电压d轴分量与q轴分量；Rs为飞轮电机的定子绕组电压；if-sd、if-sq分别为飞轮电机的定子电流d轴分量与q轴分量；Te-f为飞轮电机的电磁转矩；np-f为飞轮电机的转子转速。

2.4 定频滞环控制

采用滞环控制策略时，开关管的开通关断时刻取决于逆变器输出电流达到上、下限的时间，导致其开关频率不固定，并网逆变器输出电流谐波含量大。图7为采用三角载波技术与滞环比较器相结合的示意图。

图7 定频滞环控制策略

(12)

采用该方法，开关频率由三角载波决定，在不影响滞环控制策略的实时性、响应速度与鲁棒性的情况下，实现开关管频率固定。同时该方法无需增加额外的硬件电路，软件也易实现，进而可减小滤波器的尺寸，提高效率，降低成本。

3 仿真分析与实验验证

为验证所提出的控制方法，利用Matlab/simulink搭建了仿真平台，并通过实验进行验证。仿真过程中具有随机性、波动性的风速变化如图8所示，其系统参数如表1所示。

图8 风速变化

表1 仿真系统参数

图9与图10为采用滞环控制策略(hysteresis current control, HCC)、定频滞环控制策略(modulated hysteresis current control, MHCC)以及PWM调制方式获得的在波动的风速下的直流母线电压波形与网侧功率因数波形。由图可知，在定频滞环控制策略下，直流母线电压的波动较小，获得的网侧功率因数与PWM调制方式下获得的网侧功率因数波形相似。

图11为在恒定负载功率3 kW下，维持直流母线电压不变，飞轮储能系统输出功率的实验波形。

图12为采用不同的控制策略时网侧有功功率实验波形，图中红色曲线为采用测风速计算飞轮储能系统的充放电功率参考值的网侧功率波形，蓝色曲线为采用由网侧功率的经过高通滤波后获得的功率波动作为飞轮储能系统充放电功率参考值。由图可知，采用功率快速平滑控制策略时，电网侧的有功功率波动较小，风力发电系统的输出电能质量较高。

图9 直流母线电压波形

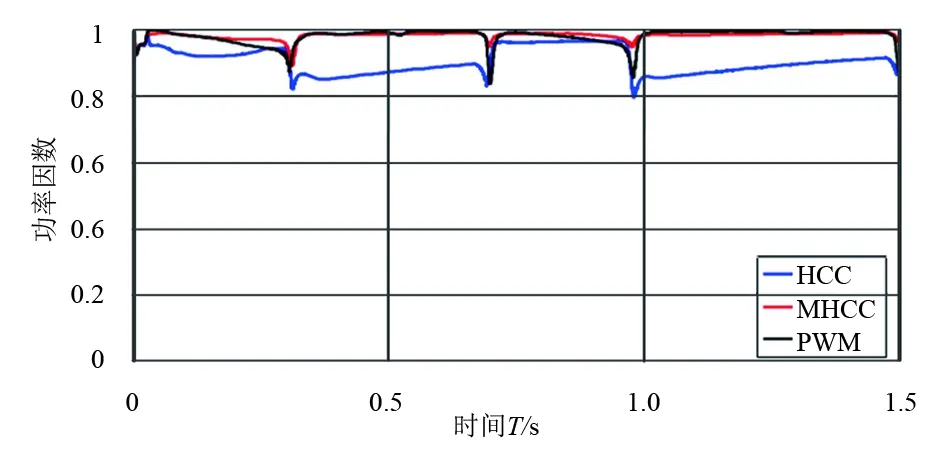
图10 功率因数波形

图11 飞轮储能系统输出功率实验波形

图12 电网侧有功功率实验波形

并网功率为10 kW时，网侧电流波形如图13所示。图13(a)中基波频率为50 Hz时，谐波含量为19.04%，而图13(b)中电流波形谐波含量为4.71%。即定频滞环控制能够显著降低网侧电流谐波含量。

图13 网侧电流波形

4 结 论

所研究的飞轮储能风力发电系统的功率快速平滑控制策略，采用网侧输入功率的高频分量作为飞轮储能系统的功率参考值，采用定频滞环控制策略避免了采用PI控制器带来的参数不稳定，以及无需锁相环。仿真与实验结果表明：该定频滞环快速功率平滑控制策略具有鲁棒性高、动态响应速度快、无静态误差等优点，还克服了开关管频率不固定、输出电流谐波含量高等问题。此外，该控制策略的算法的软硬件成本较低。