受电弓下沉对其气动和声学行为的影响

秦 登 戴志远 周 宁 李 田

西南交通大学牵引动力国家重点实验室，成都,610031

0 引言

随着高速列车运行速度的提高，空气动力学问题成为制约高速铁路发展的重要因素[1-3]。受电弓周围复杂的气流流动会导致滑板和接触线之间发生振荡和产生较强的气动噪声。已有研究表明，当列车运行速度达到300 km/h以上时，空气阻力占列车总阻力的85%以上，受电弓气动阻力占总阻力的15%以上[4]。此外，气动噪声在列车时速高于300 km时成为主导噪声，转向架、车间连接、头车鼻尖、受电弓等均为气动噪声的主要来源[5-8]。高速列车减阻降噪这个多目标优化问题随着速度的增大变得更加重要。

为了减小高速列车的运行阻力和气动噪声，目前采用的优化措施主要有：增大头车流线型长度和改变头车流线型外形[9-10]；设置半裙板或全裙板优化转向架[11]；采用半包或全包形式的外风挡优化车端连接处[12]。已有众多学者对高速受电弓的气动特性和声学特性进行了试验和数值研究[13-14]。受电弓主要由杆件组成，优化杆件的横截面形状可以有效减小空气阻力和气动噪声[15]。现有受电弓滑板横截面大多近似为矩形设计，研究表明，设计成流线型横截面时，受电弓气动阻力减小约40%左右，气动噪声减小2～5 dBA[16]。尽管受电弓的结构复杂，但通过其他合理设计也可显著减小其气动阻力和噪声。通过增设流线型导流罩、受电弓杆件表面覆盖多孔介质或进行表面微结构设计均可减阻降噪[17-19]。

随着列车运行速度的进一步提高，近年来有了新的优化方案。在列车车顶设计一个下沉式的平台安装受电弓，与受电弓直接安放于车顶上相比，列车总气动阻力减小1%～4%，同时研究表明矩形和五边形的下沉平台比其他平台更好[20]。许多研究人员对转向架和转向架腔的流动行为和声学特性进行了较为深入的研究[21-22]，但是对下沉平台所形成的受电弓腔的流动行为和气动噪声特性研究较少。并且，形成的受电弓舱很难通过某种手段对其产生的噪声辐射进行屏蔽，安装平台下沉对受电弓气动性能和远场气动噪声性能的影响规律还有待研究。

受电弓下沉安装方式目前已较为普遍，但是对受电弓舱产生的气动噪声关注却很少，腔体与受电弓部件之间的相互作用仍不清楚，因此，本文基于数值计算的方法，研究安装平台的下沉高度和倾角对高速受电弓流动行为和声学行为的影响。

1 数值计算方法

1.1 改进延迟分离涡模拟(IDDES)

受电弓由多个部件组成且大部分为杆件，其尾涡流场具有非常复杂的三维流动结构，包含了各种尺度的漩涡。直接数值模拟是对受电弓周围湍流描述最准确的方法，由于模型的复杂性，目前的计算条件还难以实现。非定常雷诺时均模拟(unsteady Reynolds-averaged Navier-Stokes, URANS)、大涡模拟(large eddy simulation, LES)以及分离涡模拟(detach eddy simulation, DES)是目前广泛采用的湍流数值求解方法[23]。URANS方法具有计算量小的优点，但它很难准确模拟出流体的瞬时脉动。LES方法可以捕捉到URANS方法无法捕捉的许多非稳态、非平衡过程中出现的大尺度效应和拟序结构，但是完全捕捉到附面层内拟序结构的演化需要非常精细的网格。

DES方法属于雷诺时均(RANS)/LES混合类方法，结合了RANS和LES方法的各自特点，减少了网格数量和计算量。SPALART等[24]在Spalart-Allmaras(SA)模型的基础上提出了SA-DES方法，这种方法对网格间距有很大的依赖性，可能会导致边界层内部从RANS提前转换为LES，并导致模化应力损耗现象。针对这个问题，SPALART等[25]又提出了延迟分离涡模拟(delay detach eddy simulation, DDES)，通过修改长度尺度的定义以确保RANS模式求解的边界层与网格分辨率无关。MENTER等[26-27]也提出了基于SST(shear stress transfer)模型的DES方法来解决模化应力损耗问题。之后又提出了改进延迟分离涡模拟(improve delay detach eddy simulation, IDDES)方法，该方法包含较多的流场上游和湍流信息，在尺度构造中包含更多的近壁信息以防止RANS和LES交界处出现雷诺应力过度下降和产生对数层不匹配现象[28]。

部分研究发现SSTk-ω和IDDES方法在模拟压力系数分布、描述流场精细结构等方面均能取得较好的结果[29]，因此，本文采用SSTk-ω湍流模型求解高速列车周围的定常流场，之后采用基于SST湍流模型的IDDES方法求解非定常流场。

1.2 FW-H方程

Ffowcs Willams和Hawkings运用广义函数理论推导出了在静止流体中做任意运动的控制面的发声方程，简称FW-H方程[30]，其积分形式为

(1)

式中，t为时间；H(f)为Heaviside函数，f=0表示有限固定表面边界区域，f>0表示无限空间边界区域，H(f)=0表示在积分曲面内，H(f)=1表示积分曲面在外；δ(f)为Dirac delta函数；2即Δ表示拉普拉斯算子；ρ′为流体密度的脉动量，ρ′=ρ-ρ0，ρ0为流场中未受扰动的密度，ρ为流场中的密度；xi、xj为直角坐标分量(i，j=1,2,3)；c0为流场声速；Q为流体与控制面相互作用导致的单极子噪声源项，Q=ρ0vn+ρ(un-vn)，un为垂直于积分表面的流体速度分量，vn为表面本身的法向速度；Fi为流体与控制面相互作用导致的偶极子噪声源项，Fi=pijnj+ρui(un-vn)，pij为应力张量，nj为积分曲面的法向单位向量；Tij为流场中湍流以及漩涡产生的四极子噪声源项，分别为流体速度在xi、xj方向的速度分量，p′为流体脉动压力，δij为克罗内克符号(当i=j时，δij=1；当i≠j时，δij=0)，τij为黏性应力张量。

式(1)等号右边三部分声源项分别对应于厚度声源、载荷声源以及四极子声源。高速列车的运行速度一般小于367.5 km/h(0.3 Ma)，对应受电弓的气动噪声主要为偶极子噪声[31]，因此，本文只考虑偶极子噪声项对高速受电弓气动噪声的贡献。

2 数值计算模型

2.1 几何模型、计算区域和边界条件

受电弓主要分为弓头(滑板、弓头支撑、弓角等)、上框架、下臂杆、拉杆、平衡杆、底架和绝缘子等几部分，对受电弓部件附属的细小结构进行了一定的简化，如螺栓等，简化后的几何模型如图1所示。

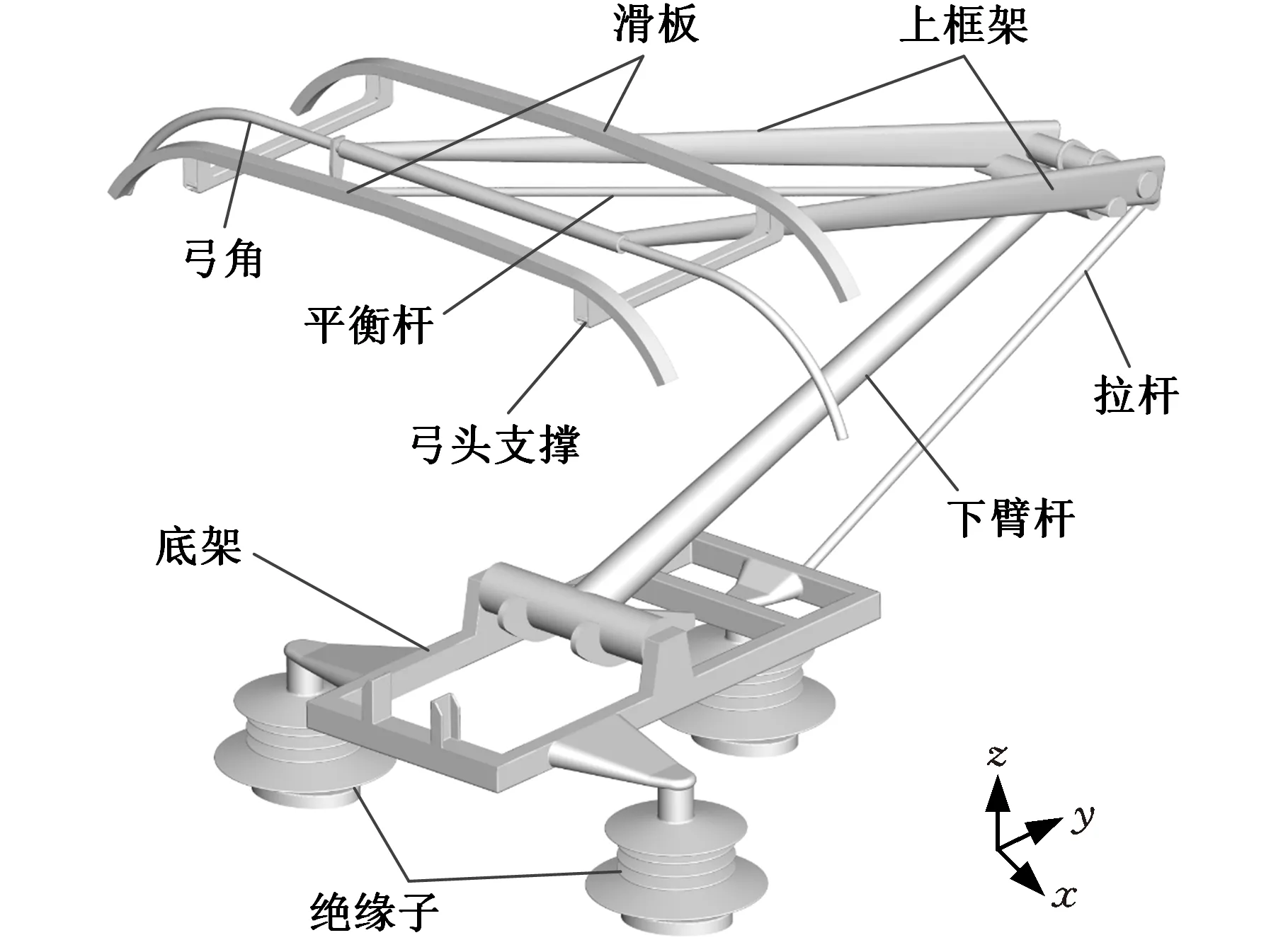
图1 高速受电弓模型Fig.1 High-speed pantograph model

为了减少网格计算量且反映受电弓下沉对列车气动阻力的影响，建立了三编组的真实列车车体模型，但忽略了转向架和转向架舱。计算区域如图2所示，计算区域长L=320 m，宽W=60 m，高H=20 m。计算域的设置满足列车空气动力学规范中的最低要求。列车位于计算区域的中心位置，计算域前表面距列车头车鼻尖的距离约为80 m；后表面距尾车鼻尖的距离约为160 m。两个侧面距离列车纵向中心截面的距离均为30 m。车底距离地面0.376 m。受电弓安装平台如图3所示，长l=3.424 m，宽w=2.354 m，高h分别为0、0.1、0.2、0.3、0.4、0.5 m；车顶与受电弓安装平台的过渡倾角α分别为0°、30°、45°、60°、90°。

图2 计算域(m)Fig.2 Calculation domain(m)

(a)三视图

(b)俯视图

(c)正视图图3 受电弓安装平台(mm)Fig.3 Pantograph installation platform(mm)

边界条件设置如下：入口设定为速度入口，速度大小为350 km/h，出口设定为压力出口，两个侧面和顶部设为对称边界，列车和受电弓表面设置为无滑移固定壁面，地面设置为滑移地面，滑移速度大小与列车运行速度相等，方向相反。当来流方向为正y时，受电弓为开口运行。若来流方向为负y方向，受电弓为闭口运行。

2.2 网格划分及独立性检验

划分3套不同尺度的网格开展网格独立性检验，计算结果如表1所示。由表1可得，网格1和网格2计算得到的整车时均气动阻力之间的误差小于0.5%。图4进一步给出了3套计算网格下，离受电弓后滑板不同距离处的流场时均速度幅值。可见，在时均气动阻力和流场物理量上网格2已经满足独立性要求。后续计算选择网格2。

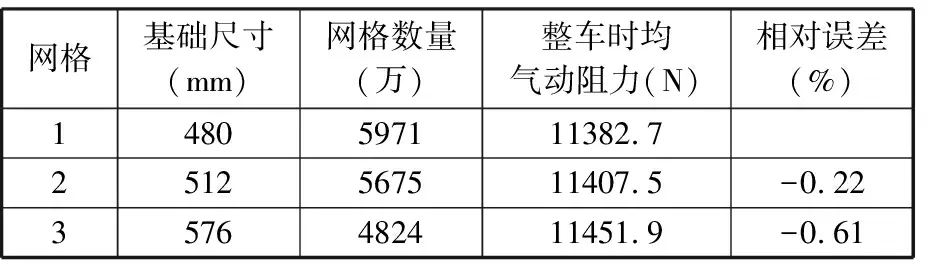
表1 网格独立性检验

图4 时均速度幅值对比Fig.4 Comparison of time average speed amplitude

网格划分的基础尺寸为512 mm，列车表面最大网格尺寸为64 mm，受电弓表面最大网格尺寸为8 mm。为保证网格过渡良好，在列车和受电弓周围进行了多次局部加密，加密区位置如图2所示，外流场网格划分结果如图5a所示。为捕捉附面层流动，在受电弓和列车表面划分边界层网格。一般划分边界层网格时与所采用的湍流模型息息相关，不同的湍流模型对边界层网格的第一层高度有所限制。理应保证边界层过渡均匀，每一层网格之间的跨度不宜过大，边界层网格层数应保证最后一层网格位于边界层之外。选取边界层的增长率为1.1，划分15层，滑板上表面边界层划分结果如图5b所示。计算网格数量约为5675万。

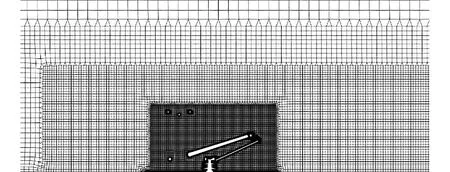
(a)外流场网格划分

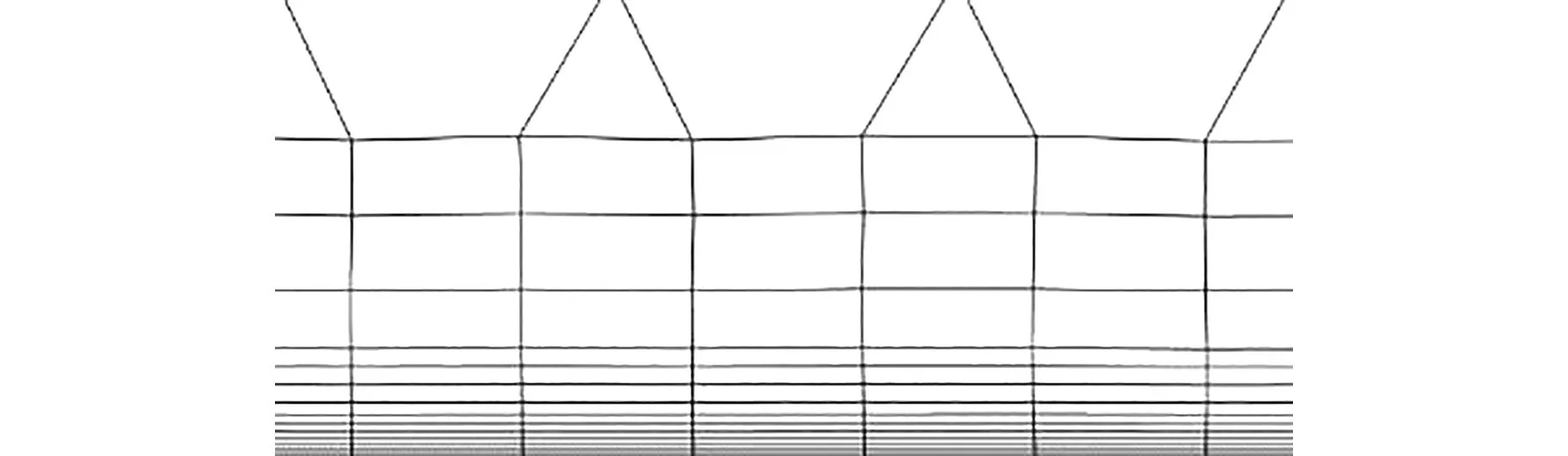
(b)滑板上表面边界层图5 网格划分Fig.5 Meshing

2.3 求解设置和噪声测点布置

利用SSTk-ω湍流模型和IDDES方法分别求解高速列车周围的定常和非定常流场。利用FW-H声学类比方程求解远场噪声。为了保证流场计算的准确性，压力-速度耦合采用SIMPLEC算法，时间项采用二阶隐式方案，对流项采用二阶迎风格式离散，扩散项采用中心差分格式离散。非定常流场和声学计算的时间步长均选取为5×10-5s，当非定常流场达到稳定后，提取受电弓以及受电弓舱表面的声源数据用于远场气动噪声输入，计算总时长为0.3 s，最大分析频率为10 kHz。

气动噪声性能评估以远场噪声测点的声压级大小和频谱特性来衡量，根据高速列车噪声测试国际标准ISO 3095-2013相关要求，测点布置如图6所示。距离轨道中心线25 m、距离轨道3.5 m高，沿列车纵向(y向)布置31个测点(yp1～yp31)，每个测点之间相距1 m。受电弓几何中心在地面的投影坐标为(0, 0, 0)m。横向布置8个噪声测点(xp1～xp8)，距受电弓几何中心的距离分别为7.5 m、12 m、15 m、25 m、30 m、40 m、50和60 m，其中xp4和yp16噪声测点重合。

图6 远场噪声测点示意图Fig.6 Schematic diagram of far-field noisemonitoring points

3 数值计算方法验证

在中国空气动力研究与发展中心低速空气动力研究所的风洞群中，分别开展了某型高速受电弓的气动力试验[32]和高速列车的气动噪声试验[33]。图7和图8所示分别为现场试验模型。气动力测试选用1/1的受电弓模型，气动力通过三台常温五分量天平测得。高速列车噪声试验选用1/8的缩比模型，在模型侧面5.8 m远处布置了30个远场传声器用于测量试验模型的远场噪声。

图7 气动试验模型Fig.7 Aerodynamic test model

图8 声学试验模型Fig.8 Acoustic test model

图9给出了受电弓气动力试验与数值计算的对比结果。开口、闭口状态下，数值模拟得到的整弓气动阻力Fd与风洞试验数据基本吻合，误差小于5%。图10给出了风速200 km/h时受电弓区域内气动噪声在数值模拟和试验之间的频谱比较。为了确保声压级不受干扰，数值模拟与风洞试验采用相同的频率带宽。由图9、图10可得，数值模拟和试验展现出较好的一致性。表2进一步给出了远场30个噪声测点的算术平均声压级对比结果，试验与仿真之间的误差小于1.5 dBA。考虑到数值仿真存在一定的误差且试验存在随机误差等，本文所采用的数值计算方法能保证一定的准确性和可靠性。

图9 受电弓气动阻力对比Fig.9 Comparison of aerodynamic resistanceof pantograph

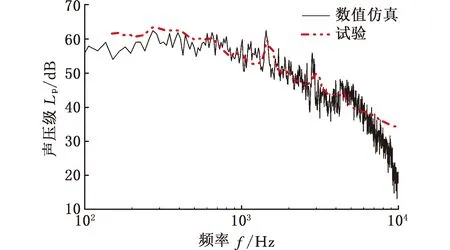
图10 受电弓频谱对比Fig.10 Comparison of the spectrum of the pantograph

表2 受电弓气动噪声对比

4 计算结果

4.1 气动行为

4.1.1下沉高度的影响

图11给出了受电弓的下沉形式，考虑到列车实际运行时接触网高度一定，平台下沉高度通过受电弓升弓来补偿。受电弓工作高度(轨道上表面到滑板顶部的距离，5300 mm)不变，受电弓下沉高度通过增大升弓高度来补偿，受电弓初始升弓高度为1290 mm。

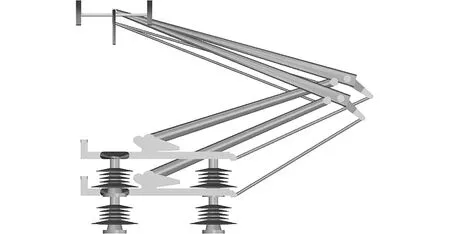
图11 受电弓下沉方式Fig.11 Subsidence methods of pantograph

图12给出了受电弓下沉300 mm和500 mm情况下的表面时均压力分布云图。受电弓气动阻力的主要来源是前后表面的压力差。受电弓安装平台下沉后改变了受电弓的下层流场结构，与安装平台无下沉相比，随着下沉高度的增大，列车前方高速气流作用在底架和绝缘子前部的正压明显减小。

表3给出了安装平台不同的下沉高度下，受电弓开口运行时各部件时均气动阻力的变化情况。安装平台的下沉高度对弓头和上框架气动阻力的影响较小。平衡杆和拉杆的气动阻力随安装平台下沉高度的增大略有增大，主要原因是以升弓方式补偿受电弓的下沉高度会导致这些部件打表4进一步给出了受电弓安装平台不同下沉高度下，受电弓开口运行时高速列车各部件的时均气动阻力。由表4可得，头车的气动阻力基本不受受电弓安装平台下沉的影响。在受电弓安装平台下沉后，尾车以及不含受电弓舱的中间车体部分的气动阻力受下沉高度变化的影响较小。受电弓安装平台下沉高度增大，所形成的受电弓舱产生的气动阻力先增大后减小。总之，受电弓安装平台下沉后，虽然会显著减小受电弓的气动阻力，但形成的受电弓舱也会产生额外的气动阻力。安装平台下沉高度h在100～500 mm范围内，高速列车整车的气动阻力先增大后减小，但均为增阻状态，阻力增大1.11%～4.44%。当h=300 mm左右时，整车阻力增加最大。

(a)升弓高度1290 mm,h=0 (b)升弓高度1590 mm,h=300 mm (c)升弓高度1790 mm,h=500 mm图12 受电弓表面的时均压力分布Fig.12 Time-averaged pressure distribution on the surface of the pantograph

表3 受电弓开口运行时各部件的气动阻力

表4 受电弓开口运行时高速列车的气动阻力

表5给出了受电弓以闭口方式运行时，高速列车各部件的时均气动阻力分布。由表5可得，各部件气动阻力的变化规律基本同受电弓开口运行时一致。安装平台下沉高度h在100～500 mm范围内，受电弓以闭口方式运行时，高速列车整车阻力增阻1.05%～3.85%。

图13给出了受电弓安装平台不同下沉高度下，纵向中心截面的压力和流线分布情况。由图13可得，受电弓安装平台下沉改变了绝缘子和底架周围的流场结构。随着下沉高度的增大，腔体前端面对受电弓下层结构的遮挡效果增强。受电弓下层结构的阻力会显著减小。此外，随着下沉高度的增大，腔体内的流动也发生显著的改变。当下沉高度h在100～300 mm时，形成的腔体较浅，腔体前端面后方和后端面前方分别形成负压和正压区域，这导致腔体产生了较大的气动阻力。

表5 受电弓闭口运行时高速列车的气动阻力

(a)开口下沉h=0 (b)开口下沉h=100 mm (c)开口下沉h=200 mm

(d)开口下沉h=300 mm (e)开口下沉h=400 mm (f)开口下沉h=500 mm图13 下沉高度对受电弓周围流场的影响Fig.13 The effect of subsidence height on the flow field around the pantograph

当下沉高度进一步增大到500 mm时，腔体较深，气流在腔体前后端面附近形成较大尺度的漩涡，后端面受到的正压作用显著减小。因此，随着下沉高度的增大，腔体所导致的阻力先增大后减小。当受电弓以闭口运行时，气流发展与开口运行时类似。

4.1.2倾角的影响

由上文分析可知，h=300 mm时整车气动阻力增加最大。图14给出了安装平台下沉300 mm时，不同腔体倾角下受电弓周围的流场。由图14可得，随着倾角的减小，受电弓下层结构受到气流的冲击作用增强，但腔体前端形成的剪切气流强度减弱，腔体前端面后方的漩涡消失且负压区域明显减小。同时腔体后端面受到气流冲击形成的正压也减小，因此，减小腔体的过渡倾角可减小受电弓舱的气动阻力。

图15给出了高速列车各部件气动阻力随腔体倾角变化的结果。由图15可得，头车、尾车以及未加受电弓舱的中间车气动阻力受倾角变化的影响较小。随倾角的减小，受电弓气动阻力逐渐增大，受电弓舱和整车的气动阻力逐渐减小。当倾角由90°减小为30°时，受电弓开口、闭口运行整车气动阻力分别减小4.8%和3.9%。与安装平台不下沉相比，受电弓开口、闭口运行时其气动阻力分别减小2.0%、1.8%，整车气动阻力分别减小1.4%、1.1%。因此，选取合适的下沉高度和腔体过渡倾角可使整车气动阻力达到最好的减阻效果。

(a)开口倾角30° (b)开口倾角45° (c)开口倾角60°

(d)闭口倾角30° (e)闭口倾角45° (f)闭口倾角60°图14 倾角对受电弓周围流场的影响Fig.14 The effect of inclination on the flow field around the pantograph

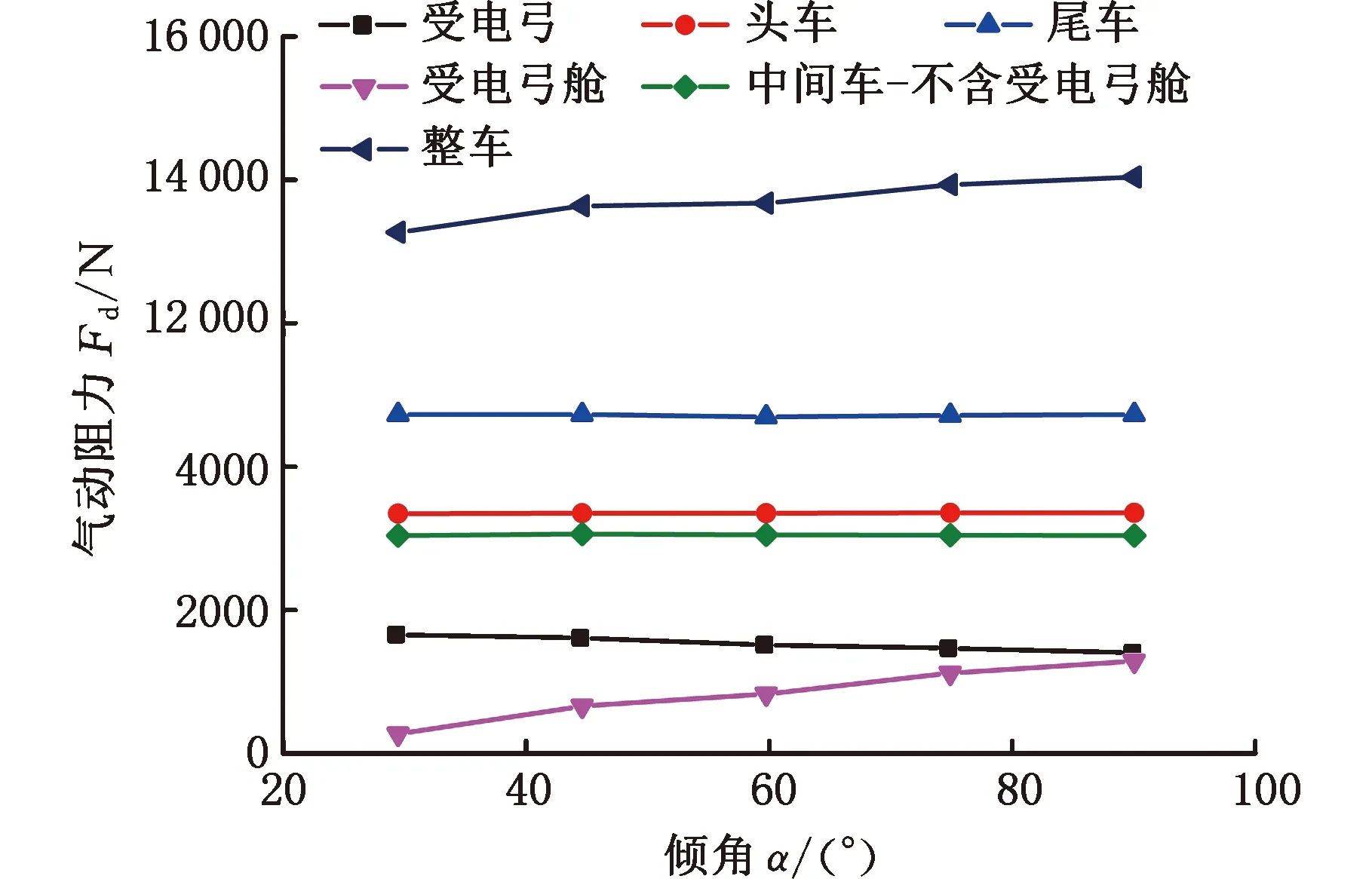
(a)开口运行

(b)闭口运行图15 倾角对高速列车气动阻力的影响Fig.15 The effect of inclination on the aerodynamicresistance of high-speed trains

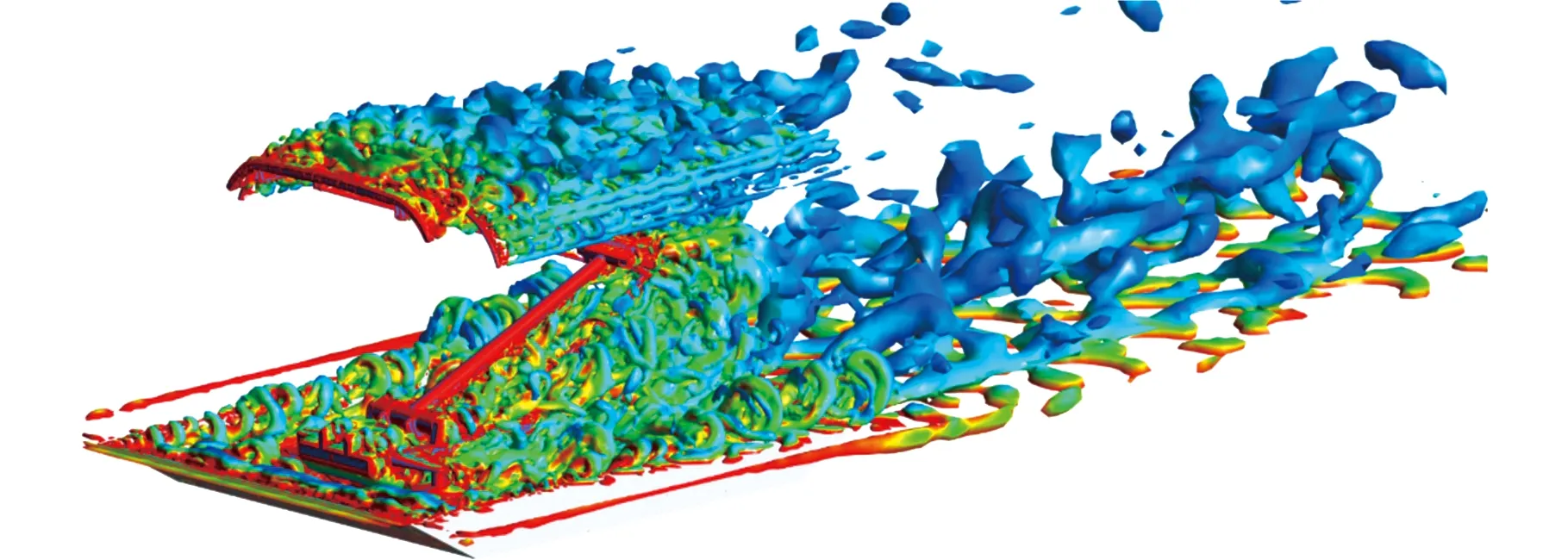
(b)h=300 mm, α=30°图16 受电弓周围涡量分布(Q=1800)Fig.16 Vorticity distribution around the pantograph(Q=1800)

4.2 声学行为

4.2.1噪声源特性

(a)h=0, α=0°

图16为基于Q准则的受电弓区域涡量分布对比图，受电弓周围区域存在尺度和旋向不同的漩涡。弓头、铰接、底架以及绝缘子区域是漩涡脱落和重组的主要部位，是受电弓的主要气动噪声源，受电弓安装平台下沉后，绝缘子和底架周围气流速度显著降低，其后部漩涡脱落强度和尺度显著减小。由于腔体的存在，受电弓下层涡旋的发展也受到一定的限制。

图17给出了受电弓表面的声功率级分布。由图17可得，受电弓安装平台下沉后，由于流场的改善，绝缘子和底架表面的声功率显著减小。绝缘子和底架区域的表面声功率级最大减小可达50 dB。可见，受电弓下沉后可显著降低其下层结构的噪声辐射强度。

(a)h=0 mm, α=0°

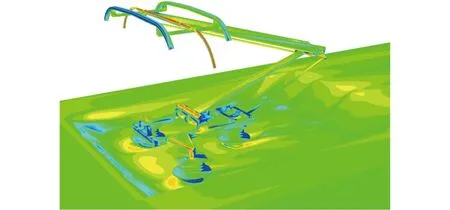
(b)h=300 mm, α=30°图17 受电弓表面声功率级Fig.17 Surface acoustic power of pantograph

4.2.2远场噪声特性

图18给出了两种工况下横向噪声测点的声压级对比结果。由图18可得，受电弓舱产生的气动噪声较小，与受电弓相比相差10 dBA以上。受电弓下沉后所产生的噪声辐射强度显著降低。与安装平台无下沉相比，安装平台下沉后受电弓下层结构(底架和绝缘子)的远场声压级最大减小4.48 dBA，整弓远场声压级最大减小2.61 dBA。

图18 横向测点声压级对比Fig.18 Comparison of sound pressure levels at lateralmonitoring points

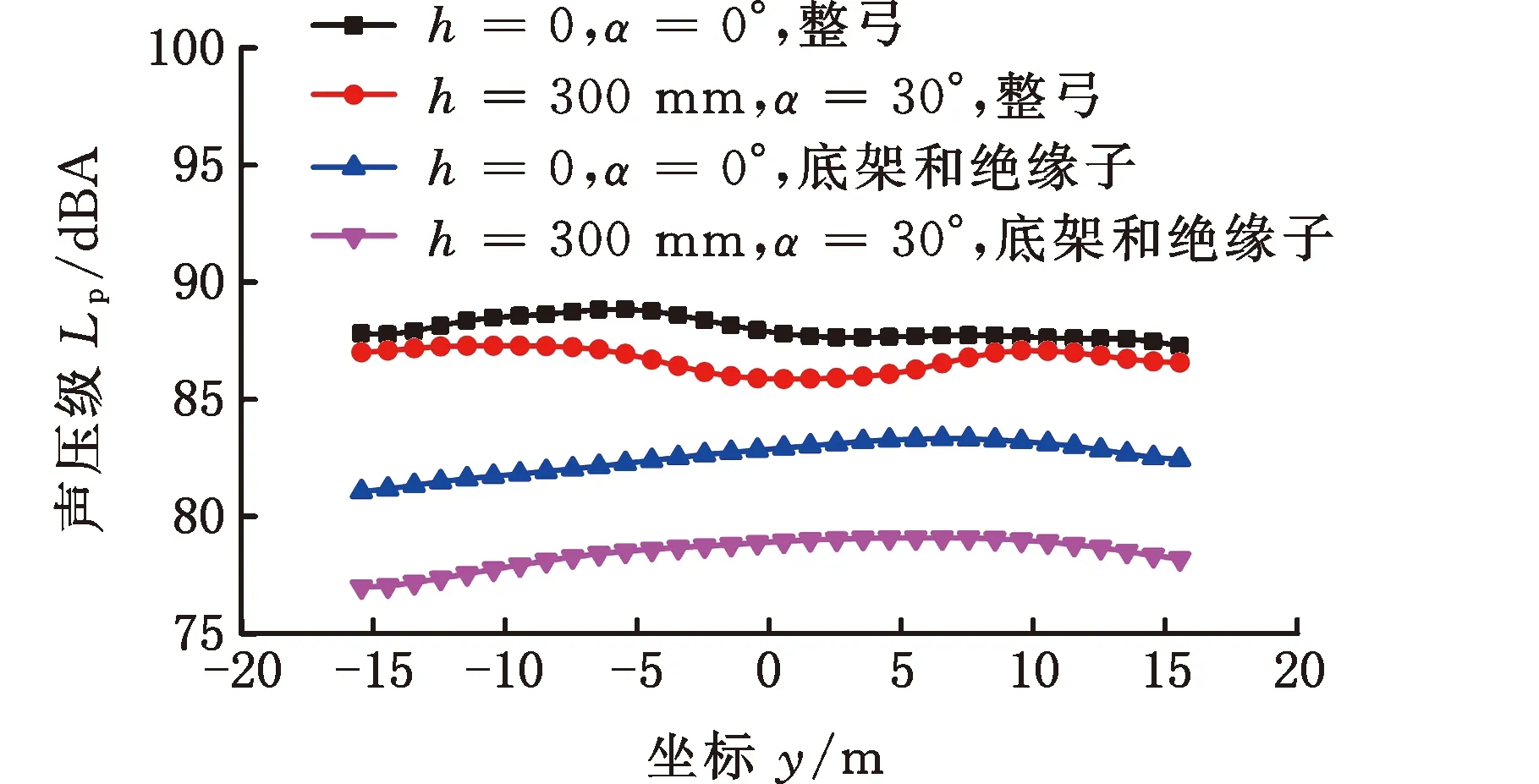
图19 纵向噪声测点声压级对比Fig.19 Comparison of sound pressure levels oflongitudinal noise monitoring points

图19给出了两种工况下，受电弓纵向噪声测点的声压级对比。与受电弓安装平台无下沉相比，下沉后受电弓下层结构的远场声压级最大减小4.25 dBA，整弓远场声压级最大减小2.02 dBA。

为了综合表示受电弓远场气动噪声的性能，以平均声压级对受电弓的气动噪声进行评估，根据能量叠加原理，平均声压级(sound pressure level)Lp的计算公式为

(2)

式中，Lpi为第i个噪声评估点的声压级，i=1,2,…,m，m为噪声测点的总数。

表6给出了两种工况下受电弓纵向噪声测点的平均声压级结果。将受电弓分为三大部分，分别为上层结构(弓头等)，中层结构(上框架、下臂杆、拉杆和平衡杆等)和下层结构(底架和绝缘子等)。安装平台下沉对受电弓上层结构的噪声影响较小，对下层结构的影响较大。下层结构减小4.06 dBA，整弓远场平均声压级减小1.31 dBA。

表6 远场平均声压级对比

4.2.3频谱特性

图20给出了平台下沉高度h=0、倾角α=0°下，yp16噪声测点处的功率谱密度。由图20可知：受电弓具有明显的主频特性，主要频率为330 Hz左右，受电弓上层结构(弓头)对主频的贡献量最大。受电弓下层和中层结构对低频能量贡献较大，上层结构对中频能量贡献较大。

图20 yp16噪声测点的功率谱密度Fig.20 Power spectral density at noise monitoring point yp16

图21给出了不同工况下，yp16噪声测点处功率谱密度的对比。由图21可知，两种工况下yp16噪声测点处功率谱密度的变化规律一致，安装平台改善了绝缘子和底架周围的流场结构。与受电弓安装平台无下沉相比，当受电弓下沉300 mm时，远场噪声测点处的噪声能量更低。

图21 yp16噪声测点功率谱密度对比Fig.21 Comparison of power spectral density at noisemonitoring point yp16

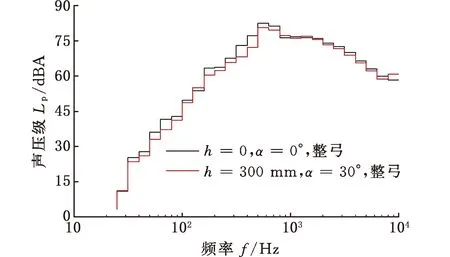
图22 yp16噪声测点处的1/3倍频程对比Fig.22 Comparison of 1/3 octave frequency at noisemonitoring point yp16

图22给出了两种工况下，yp16噪声测点处的A计权1/3倍频程。受电弓远场气动噪声的能量集中在400～2500 Hz范围内。与受电弓安装平台无下沉相比，受电弓安装平台下沉后降低了受电弓低中频范围内的噪声辐射，减小了受电弓在远场噪声测点处的声压级，改善了受电弓的气动噪声性能。

5 结论

(1)受电弓前后表面的压力差是气动阻力的主要来源。安装平台下沉后改变了受电弓的下层流场结构，绝缘子和底架受高速气流冲击的迎风面积减小致使气动阻力减小。随着安装平台下沉高度的增大，受电弓气动阻力逐渐减小。受电弓舱会产生额外的气动阻力，需通过减小腔体倾角来缓和气流使附加的阻力减小。当受电弓安装平台下沉300 mm且腔体倾角为30°时，受电弓开口、闭口运行整车分别减阻1.4%、1.1%。

(2)受电弓区域气动噪声的主要来源有弓头、框架铰接、底座和绝缘子等。安装平台下沉后，受电弓下层结构周围流体流速显著降低，绝缘子和底座表面声功率级大幅度减小。

(3)受电弓向外辐射噪声具有明显的主频特性，主要频率约为330 Hz，主要能量集中在400～2500 Hz范围。受电弓舱所附加的气动噪声相比于受电弓气动噪声更小。受电弓舱通过改善流场提高了受电弓的声学性能，降低了其噪声辐射能量。与安装平台无下沉相比，下沉300 mm且腔体倾角为30°的情况下，受电弓向外辐射的声压级最大减小2.02 dBA，平均声压级减小1.31 dBA。