航天器密封舱结构的安定分析与优化

王 新 陈 耕 刘 峰 余晨帆 张乐乐

1.北京交通大学机械与电子控制工程学院，北京，1000442.北京交通大学轨道车辆运用工程国家国际科技合作基地，北京，1000443.北京空间飞行器总体设计部，北京，100094

0 引言

密封舱是航天工程的重要组成部分，是航天器金属结构中有代表性的重要部件。密封舱的结构形式主要有半硬壳式结构和整体壁板式结构两种[1]。目前，整体壁板式结构已经成为航天器大型密封舱舱体结构的首选方案。整体壁板式结构的蒙皮与加强筋采用厚板材一体化加工形成，减少了焊缝数量从而提高了结构的密封性能，抗疲劳性能较好，结构可靠性较高[2]。由于密封舱整体结构复杂，为了使其承载更均衡，提高材料承载的利用率，需在控制质量和可靠性的基础上进行结构优化。

部分研究从舱体气动外形出发，杨肖峰等[3]对飞船返回舱结构展开分析，使用正交试验设计方法，分析结构外形主要几何参数对其气动特性的影响。李治宇等[4]通过Solidworks对返回舱基本气动外形进行结构参数化建模，以升阻比为优化目标建立优化问题进行求解，完成飞船密封舱外形的初步优化设计。李恩奇等[5]对月面着陆器上的升级压力舱进行分析，建立以整舱结构质量最小为目标的优化模型，求解得到静压载荷下舱体的最优结构形式。姚远明等[6]以密封舱结构质量最小为目标，使用ANSYS参数化语言APDL对密封舱进行参数化建模，通过对密封舱肋条布局的优化实现整体密封舱的结构优化。

对于密封舱而言，传统设计方法更多关注局部薄弱位置的强度状态来确定结构的形式和尺寸，但用最薄弱位置的局部强度来代表结构整体的承载能力往往不能满足轻量化和可靠性的共同要求。密封舱结构带有外部的壁板，初始应力状态复杂，因此使用传统设计方法对其进行分析，存在承载能力分析不到位的现象。使用安定方法进行分析可以从整体上对结构进行评估，获得结构极限承载的状态[7]。另外，从航天器相关载荷标准[8]和试验要求[9]中可以看出，密封舱在运行过程中，工况种类多，载荷复杂，载荷历史不明确。安定分析直接法可以在不了解加载历史的情况下，得到结构的承载极限。安定是指结构在变值加载下，初始阶段产生一定量的局部塑性变形后，在后续承载过程中不再产生新的塑性变形，表现为完全弹性响应的一种状态[10]。安定分析可以分析结构出现塑性变形之后的强度问题，为设计提供理论指导，因此已经广泛应用于诸多工程领域，并在一些领域的设计标准及设计规范中得到体现，如美国的ASME规范[11]、法国的RCC-MR标准[12]等。我国的国家标准《在用含缺陷压力容器安全评定》[13]和行业标准《钢制压力容器应力分析法设计标准》[14]中也都体现了安定分析理论这一思想。

在安定分析的应用方面，陈钢[15]、刘应华[16]通过极限与安定分析，全面研究了各种凹坑缺陷对压力容器结构强度的影响，提出了针对含缺陷压力容器的安全评定方法，在我国这一领域形成了较为完整的一套应用理论体系。SIMON等[17]在内点法的基础上发展新的安定分析数值方法，并应用到复杂工程结构上求解安定问题。除此之外，安定分析在海洋地基平台[18]、大型复杂机械结构[19]、铁路轨道[20]、公路路面[21]等领域的应用上也得到了验证并取得了较好的效果。另外，从国内外新一代载人飞船技术的发展来看，发展可重复使用航天器技术是降低载人航天任务成本的主要手段之一[22]。美国SpaceX公司的“天龙号”飞船、波音公司的CST-100飞船、俄罗斯的PPTS飞船，可重复使用次数均可达到10次[23]。可重复使用的要求对应的加载模式为循环载荷加载，而安定正是针对弹塑性结构在循环载荷作用下而言的。可以看出，安定方法在密封舱结构优化设计方面有很大的潜力，将设计理论推进到航空航天这一类工程应用上有广阔的前景。

在前期的工作中[24]，我们使用安定方法对密封舱进行分析，通过理论推导和数值模拟验证了方法的有效性，并通过安定分析计算，得到了典型子结构特征尺寸的最优组合。在此基础上，本文进一步提出将安定分析方法与参数化建模手段相结合，通过对密封舱轴对称参数化模型进行安定分析，从而对密封舱整体结构的厚度尺寸参数进行比选和优化。

1 基于安定分析的优化方法

(1)

根据Melan定理，安定载荷pSD可以不通过非线性有限元迭代，而是通过直接对一个优化问题求解得出，这也是安定分析被称为直接法的原因。之后使用有限元方法对结构进行离散化处理。通过数值方法描述残余应力场，使之满足平衡条件。处理后，Melan定理中的等式约束可以写成等效数值积分形式：

(2)

根据静力安定列式的约束要求，在结构中所有NG个高斯点上都要满足屈服条件，使得结构处处不违背屈服准则F：

(3)

(4)

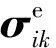
2 安定分析

密封舱实体模型规模庞大，通过安定分析数值求解此优化问题，自变量和约束的个数都在百万级别以上，求解时间长，难以直接用于以安定强度为目标的结构设计与优化。由于密封舱的结构形式以及所承受的载荷都是对称的，因此可以选用轴对称模型进行转换。与实体模型相比，轴对称模型规模较小，求解时间较短，且与参数化建模手段结合较为方便。在我们先前的研究中[24]，对结构分别使用六面体实体单元和四边形轴对称单元进行分析，得到的结果相同，证实了计算所得安定极限的客观性。我们也对试验密封舱分别使用这两种单元，在相同工况下进行了弹性分析。密封舱材料模型参数如表1所示，所受载荷为作用在舱体内壁上的0.15 MPa内压载荷。对于实体有限元模型，单元统一为线性六面体全积分单元C3D8，模型共含有253 776个单元及436 621个节点，边界条件及分析得到的应力场如图1所示；对于轴对称有限元模型，单元统一为线性轴对称四边形全积分单元CAX4，模型共含有9594个单元及11 375个节点，边界条件限制对称轴上最底端节点z方向上的位移。分析结果显示两者应力场分布相近，最大应力位置均出现在底面拐角处，局部位置Ⅰ处实体模型截面与轴对称模型应力场如图2所示。结合上述分析可以看出，在密封舱结构设计优化上，实体模型和轴对称模型有着近似的特征，将实体模型转换为轴对称模型进行分析具有合理性。

表1 密封舱模型材料参数

图1 密封舱实体模型边界条件及应力场Fig.1 Boundary conditions and stress field of airtightcabin solid model

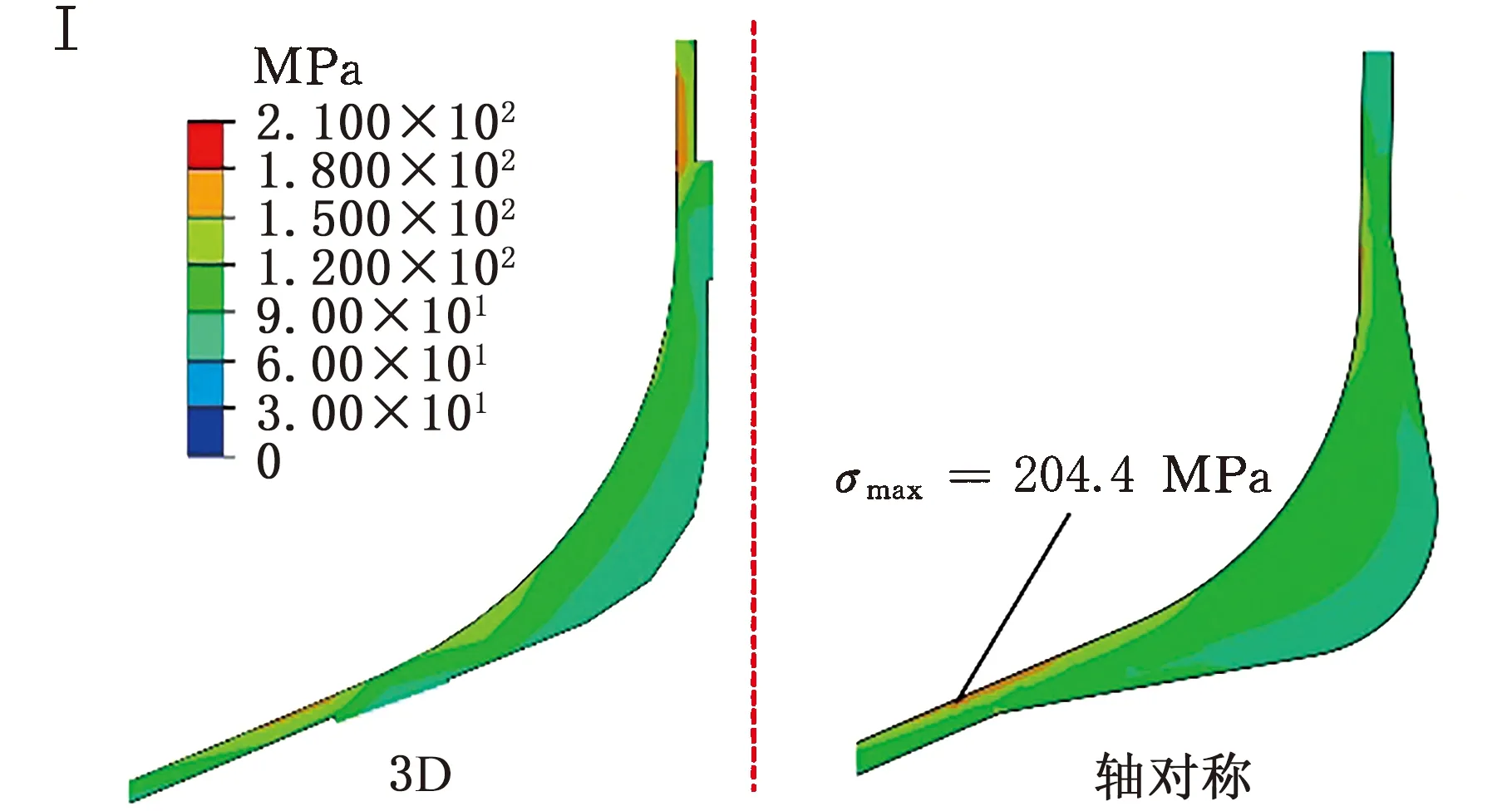
图2 密封舱实体单元与轴对称单元结果Fig.2 Results of airtight cabin solid element andaxisymmetric element

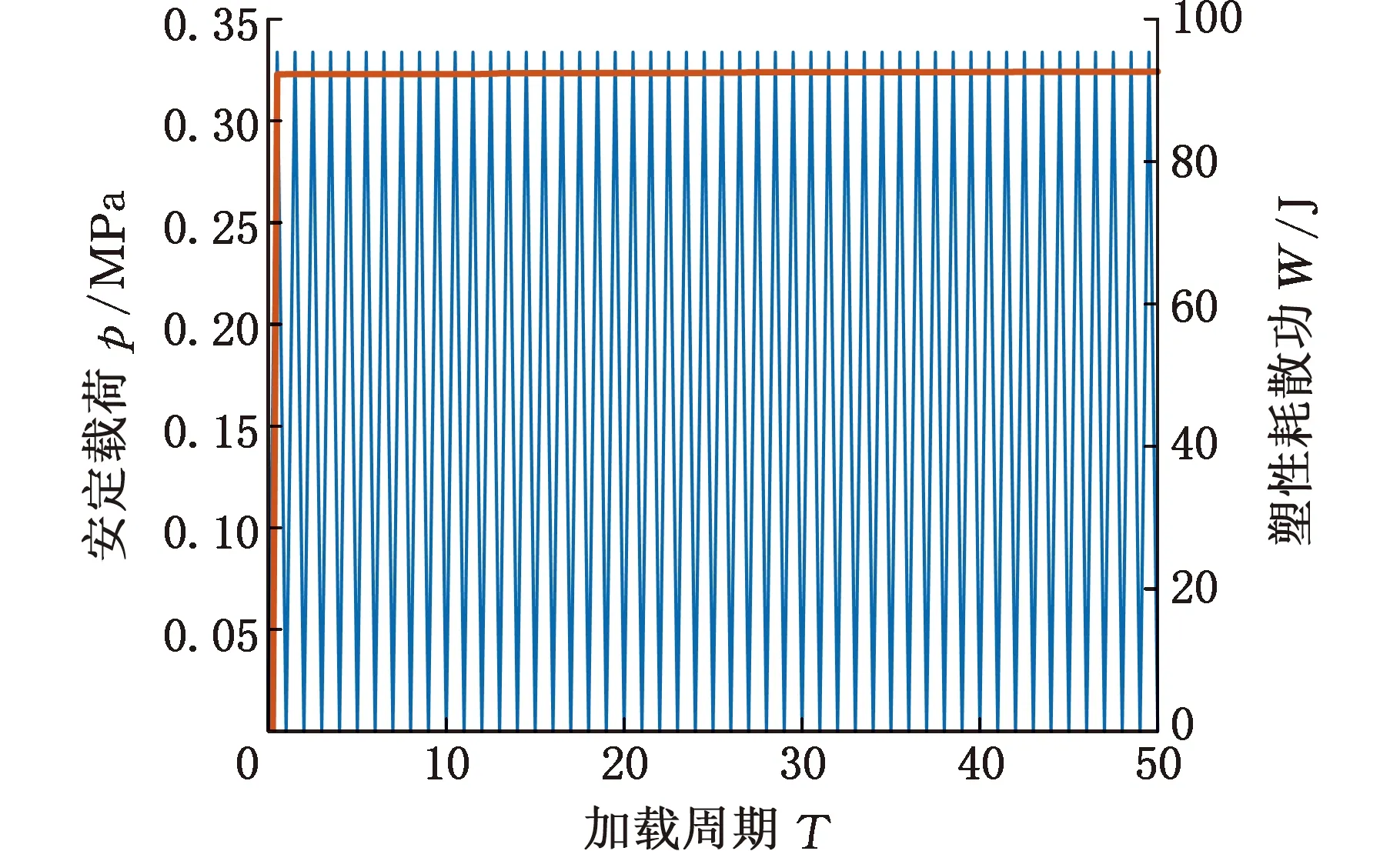
图3 加载路径及塑性耗散能Fig.3 Loading path and plastic dissipated energy

通过轴对称单元对密封舱进行安定分析，得到结构的安定载荷为0.3338 MPa。弹性极限为0.1669 MPa。为了检验安定分析结果的真实性，进行有限元循环加载模拟。如图3所示，将0.3338 MPa的安定载荷以50个周期的形式施加在舱体中，对模型中的总塑性耗散能进行分析，从中可以看出，伴随着载荷周期的不断累积，总塑性耗散能趋于稳定。说明结构不发生新的塑性变形，分析结果真实，结构处于安定状态且对应的失效形式为交变塑性。

3 轴对称的参数化模型

在上述现有试验舱结构的基础上，考虑更多的设计参数，建立图4所示新的密封舱轴对称参数化模型。轴对称模型对应着圆柱坐标系(R,θ,Z)，其中R、θ和Z分别代表径向、周向和轴向。模型单元统一为线性轴对称四边形全积分单元CAX4。涉及到的材料参数如表1所示。按照试验要求，模型所受载荷为作用在舱体内壁上的0.15 MPa内压载荷。同时为了避免刚体位移，限制对称轴上最底端节点z方向上的位移。

图4 密封舱参数化模型Fig.4 The parametric model of airthght cabin

图4中t1～t5为参数化建模中主要可变参数(以下单位均为mm)：t1范围为[3.0,5.0]，t2范围为[2.0,4.0]，t3范围为[2.0,4.0]，t4范围为[2.0,4.0]，t5范围为[6.0,8.0]。t1～t5均在各自范围内取整数。在上述参数之外，圆角尺寸等也均可在参数化建模程序中作为可变参数进行修改，方便后续对拐角处细节进行调整。原始构型设计参数为t1=5 mm,t2=3 mm,t3=3 mm,t4=4 mm,t5=6 mm，记为构型A。

4 密封舱结构的安定分析与优化

针对轴对称的参数化模型，根据第1节介绍的安定分析方法，结合参数化建模脚本批量化进行安定分析。在批量化安定分析的基础上，对轴对称模型中的可变参数t1～t5进行参数敏感度分析，在该分析中每次仅改变参数t1～t5中的一个，并使其余4个参数依次分别取其区间的最小值、中位值以及最大值。单参数敏感度分析结果如图5所示。

(a)t1参数敏感度分析

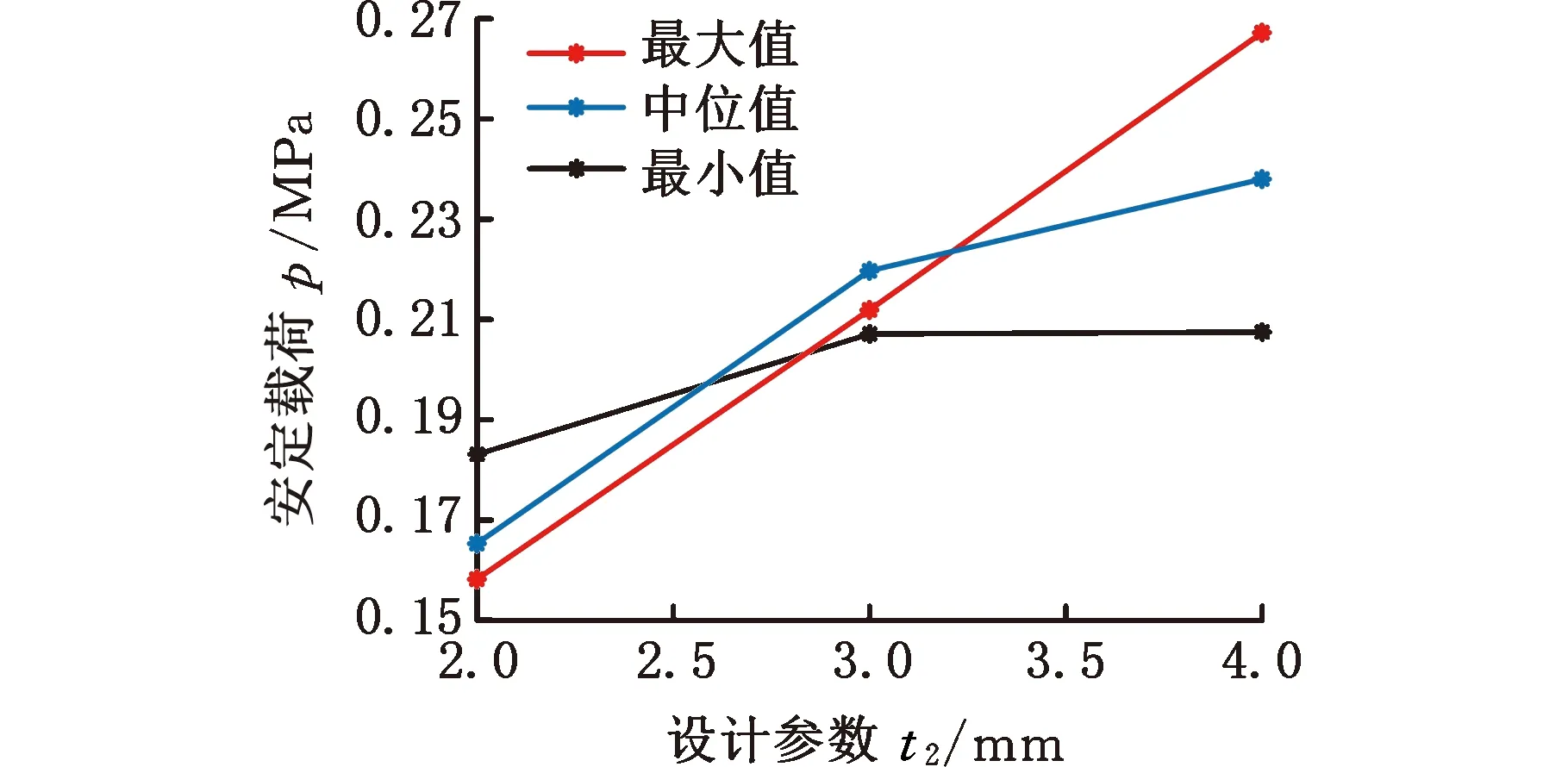
(b)t2参数敏感度分析

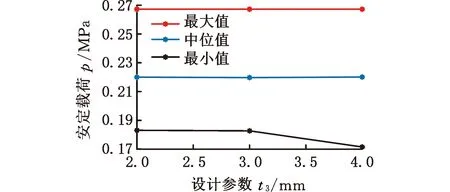
(c)t3参数敏感度分析

(d)t4参数敏感度分析

(e)t5参数敏感度分析图5 单参数敏感度分析Fig.5 Single parameter sensitivity analysis

在t1～t5参数中，单参数t2敏感度较高,且无论其余4个参数取值如何，结构的安定强度与t2均保持了正相关性。除此之外，无论其余参数如何取值，单参数t5对结构的安定极限基本没有影响。这一现象原因在于在本研究所涉及的参数变化区间内，结构的薄弱位置始终保持在舱体底部，这一位置与尺寸t5关系较弱，因此结构承载能力基本不受这一参数的影响。需要说明的是，密封舱的安定极限受局部应力水平的影响。考虑到局部应力分布不仅受t1～t5参数的影响，也同样受拐角处尺寸的影响，因此，后续研究将对拐角处尺寸对结构安定强度的具体影响进行探究，从而进一步系统地评估如何通过改变拐角处形状参数实现密封舱构型的局部优化。

考虑到单参数敏感度分析的局限性以及各参数间可能存在的耦合关系，在单参数分析的基础上进一步进行双参数组合下的敏感度分析。在该分析中将依次同时改变参数t1～t5中的2个，并保持其余3个参数的取值为其区间的中位值。部分双参数组合下的安定载荷极值结果如表2所示。除最敏感的参数t2外，t1、t3、t4、t5两两进行双参数组合下的敏感度也较低，而包含最敏感的参数t2时，双参数组合下的敏感度较高。即并未发现单参数敏感度分析中某两个敏感度较低的参数组合后敏感度变得较高，因此从双参数敏感度分析中可以看出，参数间耦合关系较弱。

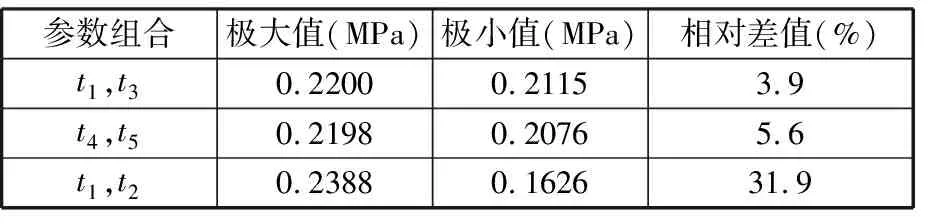
表2 双参数组合下安定载荷

需要说明的是，由于安定方法本身的计算复杂性，考虑高维设计空间将耗费大量计算时间，因此，从工程实际出发，我们选取了几个关键设计参数，并将耦合参数限定为两个，从而方便从安定强度的角度理解设计参数之间的关系。原则上本文提出的方法可用于多参数情况的结构优化，但其实际使用的条件是计算效率必须提高到一定程度。

在不同的参数组合下，选取100组安定载荷计算结果及相对应的总质量大小来进行结果分析。散点图6中展示了不同参数组合下，相应的总质量m与安定载荷p。

图6 参数化分析中质量与安定载荷Fig.6 Mass and shakedown load in parametric analysis

对批量化安定分析结果进行讨论，原始构型A对应的安定载荷在图6中A点示出。从图中红线可以看出，在结构整体质量基本相同的情况下，不同的参数组合对应的安定载荷存在较大区别。因此能够在控制质量不变的前提下，通过选取合理的参数组合获得较大的结构安定强度。图6中B点对应的构型记为构型B，其质量与构型A几乎相同，但却对应着较大的安定载荷。构型B相应的参数组合为t1=5 mm,t2=4 mm,t3=2 mm,t4=4 mm,t5=6 mm。在图4所示拐角Ⅱ处，两种结构分别对应图7所示的纯弹性应力场。从弹性应力场云图中可以看出，应力的较大值出现在底面的拐角处位置，该位置的结构较为薄弱。计算得到构型A的弹性极限为0.1082 MPa，安定载荷为0.2164 MPa。构型B的弹性极限为0.1312 MPa，安定载荷为0.2624 MPa。对构型A、B的安定分析结果进行验证，有限元循环加载方式与图3相同，同样将对各构型分析得到的相应安定载荷以50个周期的形式施加在舱体中，对总塑性耗散能进行分析。从图8可以看出，伴随着载荷周期的累积，构型A、B的总塑性耗散能都趋于稳定，结构不发生新的塑性变形并处于弹性安定状态。对于这两种构型而言，虽然其质量几乎相同，但通过安定分析得到的安定载荷却相差较大。换言之，在密封舱结构设计阶段，可以通过合理的结构布局来提高其整体的承载能力。

图7 Ⅱ处构型A、B弹性应力场Fig.7 The elastic stress field of configuration A andB at Ⅱ area

(a)构型A塑性耗散功及其时间导数

(b)构型B塑性耗散功及其时间导数图8 塑性耗散功及其时间导数Fig.8 Plastic dissipation energy and its time derivative

5 结论

本文介绍了对密封舱结构进行安定分析所使用的优化方法，说明了针对密封舱结构优化问题，将实体模型转化为轴对称模型进行分析的合理性和可行性，并对密封舱轴对称的参数化模型进行了分析，得出的主要结论如下：

(1)通过对轴对称模型的分析，质量几乎相同的不同密封舱构型，与安定极限标志的承载能力有约20%～25%的差距，说明密封舱结构在保持质量不变的前提下，可以通过优化结构尺寸有效提高承载能力。

(2)单参数敏感度分析中，相比于其他参数，参数t2敏感度较高，且与安定强度呈现出正相关性。双参数敏感度分析中，参数间耦合关系较弱，双参数中包含最敏感的参数t2时敏感度较高。对于该密封舱模型，下部拐角处附近壁厚尺寸对结构安定强度的影响较大。