掘进机截割臂自适应截割控制策略研究

王东杰 王鹏江 李 悦 郭明泽 郑伟雄 沈 阳 吴 淼

中国矿业大学(北京) 机电与信息工程学院，北京，100083

0 引言

我国煤炭资源储量大、分布广，但储存条件复杂，煤炭开采主要以井工方式进行[1]。2020年3月国家发改委、国家能源局等八部委联合印发的《关于加快煤矿智能化发展的指导意见》，要求大力推进煤矿智能化建设，到2025年实现采掘、运输等各系统的智能化决策和自动化协同运行[2]。悬臂式掘进机是煤矿井下综掘工作面最重要的设备，其自动化、智能化水平是实现无人智能掘进、提高掘进效率的关键[3-4]。掘进机截割臂与截割头是掘进机的核心截割部件，掘进机依靠截割臂的摆动与截割头的转动来实现巷道煤岩的截割；截割臂在摆动截割过程中，井下巷道断面所截割煤岩的硬度与密度会不断变化[5]，截割臂摆速不能根据煤岩硬度变化进行实时调节，为提高掘进效率，延长截割部使用寿命，有必要对掘进机截割臂摆速进行高效调控，使截割臂摆速可以根据煤岩硬度的变化进行自适应调节。

国内外学者针对自适应截割展开了研究。高峰等[6]提出了一种截割臂摆速自动控制方法，通过实时监测截割电机电流，并以额定电流作为判断依据，基于PID控制方法对截割臂摆速进行自动控制；贺文海等[7]提出了一种基于模糊PID的掘进机恒功率控制系统，以油缸线速度误差及误差变化率作为输入，通过模糊PID控制器对截割臂摆速进行调节。国外一些研究机构如瑞典SANDVIK、美国TEREX公司等针对掘进机截割臂摆速控制研发了负载敏感型液压阀，可基于油缸压力对截割臂摆速进行自适应调节[8]。以上对掘进机自适应截割的研究均是基于截割电机电流或油缸压力单一参数来判断截割载荷，单一参数不能全面、稳定地反映当前截割载荷的变化，无法准确给出摆速调控依据；此外，现有截割臂摆速控制方法的智能化程度较低，对井下截割效率提升有限。

基于以上分析，笔者提出一种基于多传感器信息的截割臂摆速自适应截割控制策略。基于井下实测多传感器信息，采用径向基函数(radial basis function, RBF)神经网络设计载荷识别器，得到可表征煤岩硬度的截割载荷信号；以截割载荷信号作为摆速调控依据，采用遗传算法优化的模糊PID智能控制器对截割臂摆速进行智能调节，实现截割臂依据煤岩硬度变化自适应截割，并对具体调速方法及控制策略进行了仿真分析和井上工业性实验验证。

1 多传感器信息数据采集及载荷分析

掘进巷道工作环境特殊，掘进机截割头的截割载荷不能通过测力装置直接得出，需通过截割状态参数来间接识别。截割电机电流、截割臂驱动油缸压力、截割臂振动加速度都是与截割状态密切相关的物理参数，因此首先通过实验实现对3个截割状态参数的实时测取。

1.1 截割状态参数分析

1.1.1截割电机电流

掘进机截割时，截割头在截割电机带动下高速旋转破碎煤壁，截割头受到煤岩反作用的截割阻力，截割头截割阻力、截割头转速、截割电机输出转矩和截割电机有功功率的关系为

(1)

式中，F为截割头截割阻力；T为截割头输出转矩；D为截割头直径；P为截割电机有功功率；n为截割电机转速；I为截割电机电流；U为截割电机输入电压，通常为1140 V；φ为截割电机电压与电流之间的相位差。

联立式(1)三式并化简得

(2)

由式(2)可得，在其他条件一定时，截割阻力变大时，截割电机电流会随之增大。

1.1.2驱动油缸压力

掘进机截割过程中，截割头高速旋转时，截割臂需在驱动油缸作用下横向或者纵向摆动，截割出完整断面，当截割载荷变大时，驱动油缸提供的横向摆动力和纵向摆动力会随之增大，因此可根据油缸油路压力信号评估截割载荷大小。

1.1.3截割臂振动加速度

巷道环境复杂、恶劣，经常会出现冲击性载荷，掘进过程中掘进机普遍会产生振动，载荷越大振动越强，且越靠近截割头振动变化越剧烈，因此截割臂处振动的剧烈程度可反映载荷大小。

1.2 实验方案

井下实验地点为冀中能源公司的邢东矿，实验机型为石家庄煤矿机械有限公司生产的EBZ135型掘进机，测试巷道断面为斜矩形，掘进长度约200 m；根据掘进机的结构特点及工作特性，选用符合煤矿安全标准的BYD-60型矿用压力变送器，串联两个回转油缸的有杆腔及无杆腔来测取输出的两路油压信号p；选用矿用本质安全型GBC1000加速度传感器检测截割臂振动加速度信号a，传感器布置在振动最强的截割臂前端；截割电机电流由掘进机的机载状态检测器给出。实验采样频率为1 Hz，实验使用本研究团队自主研发的煤矿井下采掘设备机载大容量数据记录仪来储存、发送采集到的多传感器实测数据[9]。

1.3 实验数据处理

经过井下几十个完整工作周期的截割状态监测，所采集的多传感器信息可全面充分表征各个工况下的截割载荷；但在截割状态信号采集过程中，由于井下非常复杂的工况环境，会出现数据的极端异常值，这些异常值的存在会影响神经网络载荷识别模型的训练，导致截割载荷识别精度降低。本文采用3σ准则对数据进行处理：

xi-μ>3σ

式中，xi为所采集数据组中的个体值；μ为所采集信号数据的平均值；σ为数据的标准偏差。

将所采集到的3个传感器信号数据分别应用于此准则，将满足上式的数据剔除，同时剔除时序相同的同一组其他数据。井下实测获得的部分样本数据如表1所示。

表1 井下实测部分样本数据

1.4 截割载荷分析

通过提取不同截割工况下的多传感器信息数据组{I，p，a}，并结合课题组前期研究所得截割头载荷计算方法[10]，得到不同截割工况下对应多传感器数据组及截割载荷范围，如表2所示。

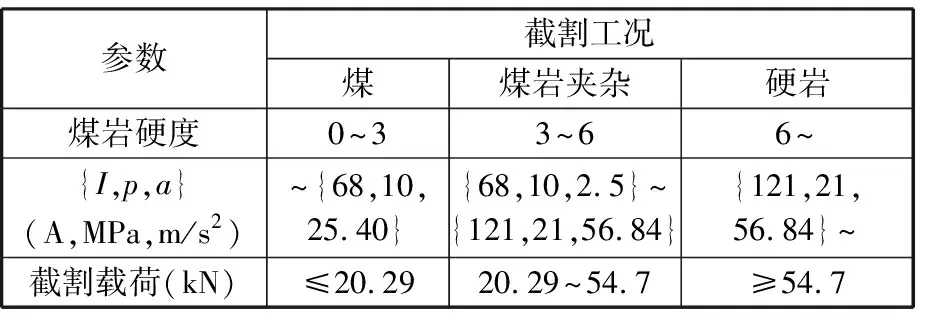
表2 不同截割工况下对应多传感器数据组及截割载荷范围

基于不同截割工况下对应的多传感器数据组及截割载荷范围，同时在井下大量完整截割周期实测多传感器数据支撑下，可利用神经网络多信息融合技术，精准识别截割载荷信号，为不同煤岩硬度工况下截割臂的摆速调控提供准确依据。

2 截割臂自适应截割控制策略

2.1 截割臂摆动工作原理

悬臂式掘进机属于部分断面掘进机，由回转台、截割头、液压缸、机身等组成，井下截割断面成形过程中，截割头高速旋转，同时截割臂沿着一定截割路径进行摆动使煤岩破落，横向截割时，在回转油缸作用下水平摆动，纵向截割时，在升降油缸作用下垂直摆动，反复水平、垂直摆动多次，最后截出完整断面[11]。截割臂结构及摆动示意图见图1。

(a)截割臂横向摆动示意图

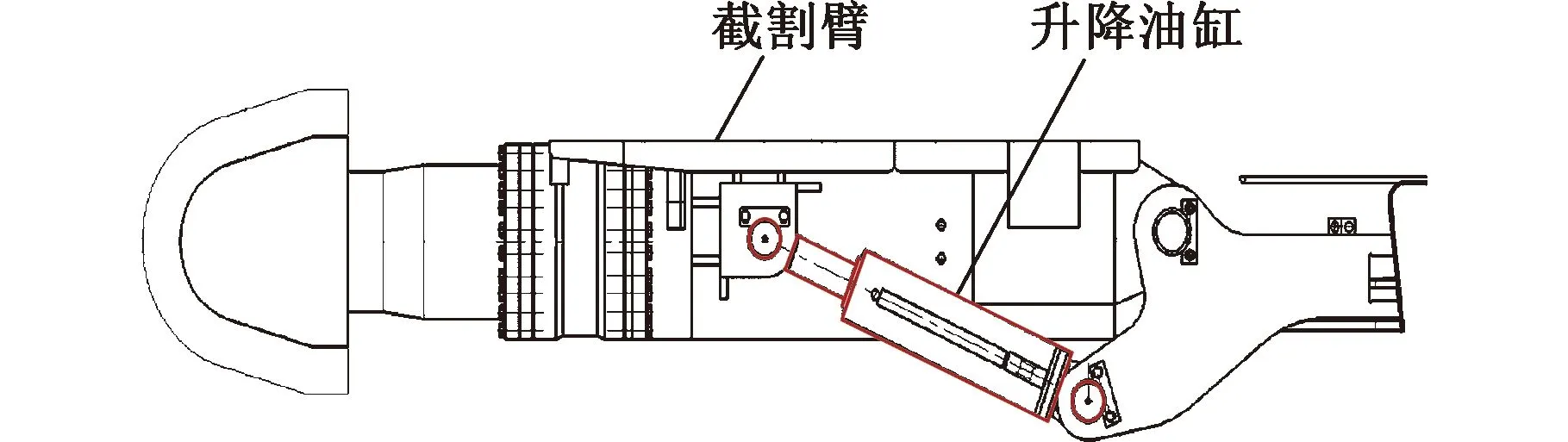
(b)截割臂垂直摆动示意图图1 截割臂结构及摆动示意图Fig.1 Structure and swing diagram of cutting arm

2.2 截割臂自适应截割控制策略

掘进机截割过程中，截割电机电流I、截割臂驱动油缸压力p、截割臂振动加速度a虽然都是可有效反映截割载荷大小的物理参数，但它们与截割载荷之间无法建立精确的数学计算模型[12]。RBF神经网络作为一种性能强大的前馈型神经网络，适合解算内部机制十分复杂的问题[13]，因此本研究以上述3个截割状态参数作为状态监测变量，采用RBF神经网络构造载荷识别器识别截割载荷信号，得到摆速调控依据。

针对复杂且时变的截割臂摆速控制系统，构造经遗传算法优化的模糊PID智能控制器，该控制器在传统PID控制的基础上，采用模糊控制在线调整PID控制参数，并利用遗传算法自动寻找最优初始控制参数，使控制系统性能在截割过程中始终得到保证。

综上，截割臂自适应控制策略分为两个模块：截割载荷信号识别模块和摆速控制模块。RBF神经网络载荷识别器通过井下实测多传感器数据进行离线训练，截割过程中，将实时采集的截割电机电流I、截割臂驱动油缸压力p、截割臂振动加速度a输入到已训练好的RBF神经网络载荷识别器，输出为表征煤岩硬度的截割载荷信号F；摆速控制模块以截割载荷信号F为驱动控制变量，转换为期望摆速，并利用遗传算法优化的模糊PID智能控制器对截割臂摆速完成调控，最终实现摆速自适应调节。自适应截割控制策略如图2所示。

3 RBF神经网络载荷识别器设计

3.1 RBF神经网络构建

RBF神经网络是一种三层前向神经网络，包括输入层、隐含层、输出层三层结构[14]，根据上述建立的控制策略，神经网络控制器的输入层设定的3个神经元分别对应截割电机电流、截割臂振动加速度、液压油缸压力3个截割状态参数；输出层设定1个神经元，对应输出为归一化后表征截割载荷信号(F)大小的量纲一数值。具有3-m-1结构的RBF神经网络拓扑结构如图3所示。

图2 自适应截割控制策略框图Fig.2 Control strategy block diagram

图3 RBF神经网络拓扑结构Fig.3 Topology of RBF neural network

3.2 RBF神经网络训练

RBF神经网络的隐含层径向基函数是对中心点径向对称且衰减的非负非线性函数，选用高斯函数作为隐含层神经元的传递函数，假设隐含层神经元有m个，此时第i个隐含层神经元的输出为

(3)

式中，ci、σi分别为隐含层第i个神经元基函数的中心和宽度；x为截割状态参数的三维输入向量；‖x-ci‖为x-ci的欧几里得距离。

隐含层到输出层是线性映射的，故神经网络的总输出为隐含层神经单元输出的线性加权和：

(4)

式中，wi为第i个隐含层神经元到输出层的连接权值。

RBF神经网络的训练过程实际是不断调整基函数的中心ci、宽度σi以及隐含层与输出层连接权值wi，从而使神经网络输出结果与实际值误差最小的过程，其训练逼近的目标误差函数为

(5)

式中，N为训练样本数。

为使目标误差函数最小化，采用梯度下降法对RBF神经网络进行自监督训练，基函数中心调整公式为

(6)

式中，k为迭代次数；η为学习速率。

基函数宽度调整公式为

(7)

输出连接权值调整公式为

(8)

根据式(3)～式(8)训练算法对设计的RBF神经网络进行训练，为避免多种传感器数值量纲问题，训练前将所有数据归一化处理。为确定隐含层神经元数，选取2000组归一化后数据对包含不同神经元数的神经网络进行训练，设定最大迭代次数为100、设定目标误差为1×10-3，不同神经元数的训练结果误差如图4所示。

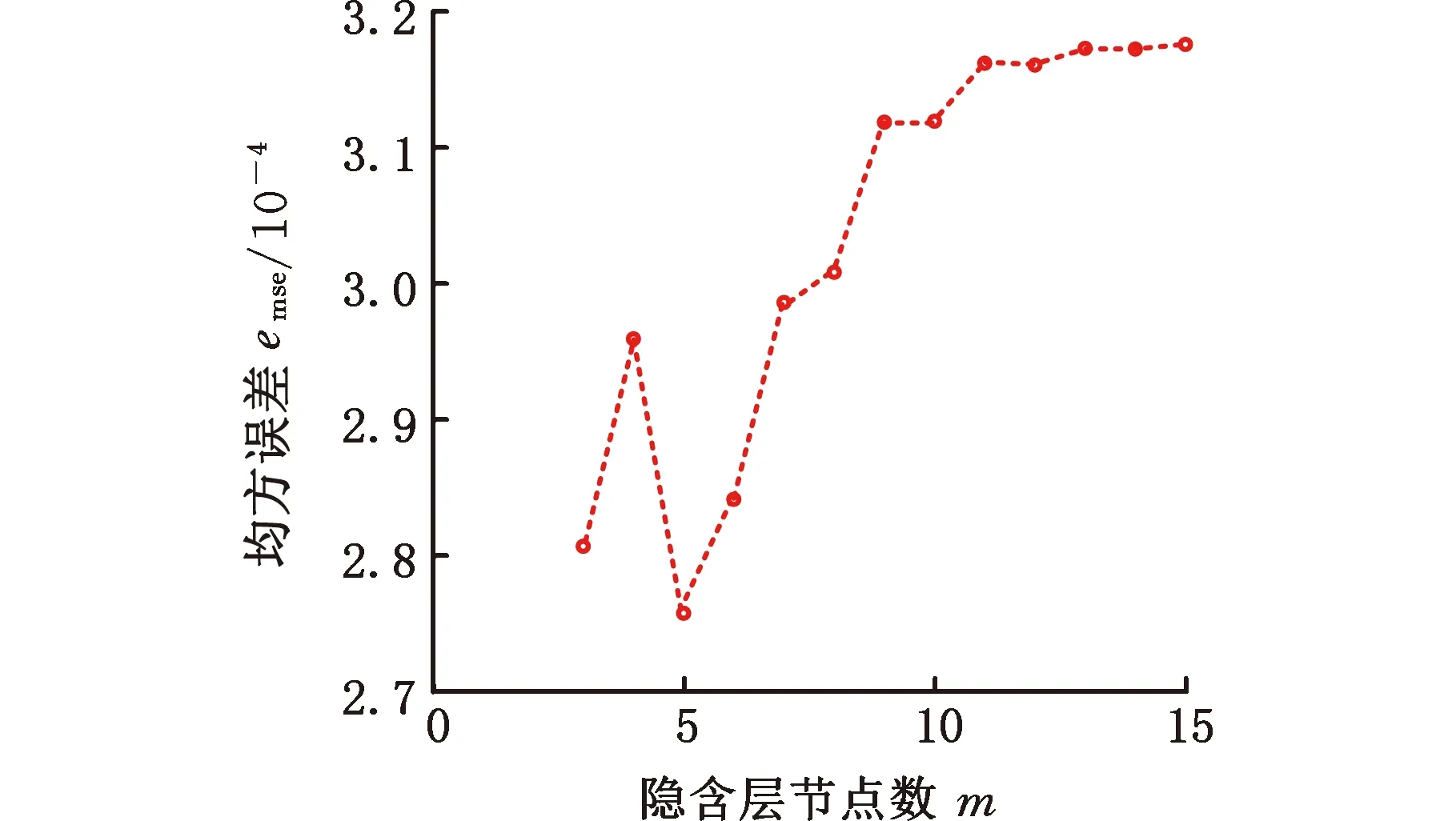
图4 不同隐含层神经元数对应的训练误差Fig.4 Training error of different hidden layer neurons

由图4可知，在相同条件下，当隐含层神经元数为5时，神经网络训练误差最小，且可达到目标误差。因此设定RBF神经网络隐含层神经元数为5，目标误差为1×10-3，继续选取500组井下实测数据对建立好的RBF神经网络进行训练，设定迭代次数为100，并另取100组实测数据对训练好的神经网络进行测试。训练与测试结果如图5所示。

由图5a可得，经过约15次迭代后训练结果与测试结果都达到误差要求；迭代完成后多传感器信息数据测试集的期望值与预测值结果对比如图5b所示，随着多传感器输入数据的不断变化，训练好的神经网络预测值结果与期望值基本一致，测试集相对误差如图5c所示，平均误差小于1×10-3，可以满足掘进机截割载荷信号识别要求。

(a)迭代过程

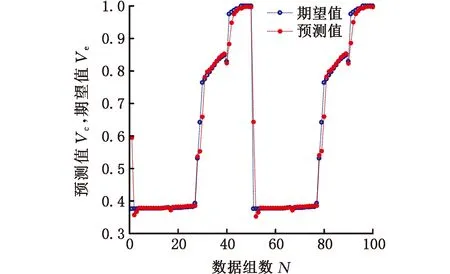
(b)测试集期望值与预测值对比

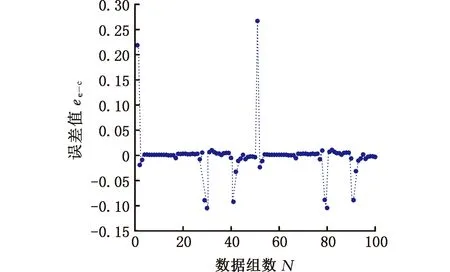
(c)测试集期望值与预测值的误差图5 训练与测试结果Fig.5 Training and test results

4 模糊PID控制器设计及遗传算法优化

传统PID控制不具备在线调整能力，采用模糊控制器对PID控制参数在线调整(简称FPID控制器)，以适应时变的截割臂摆速调整系统。此外，由于模糊PID控制器初始控制参数常采用试凑法、临界比例法等手动计算方法得到，智能化程度低，控制效果差，因此针对模糊PID控制器，设计遗传算法(genetic algorithm，GA)自动寻找其最优初始控制参数，使截割臂摆速得到精准快速调控。基于遗传算法优化的模糊PID控制器简称GA-FPID控制器，GA-FPID控制器结构如图6所示。

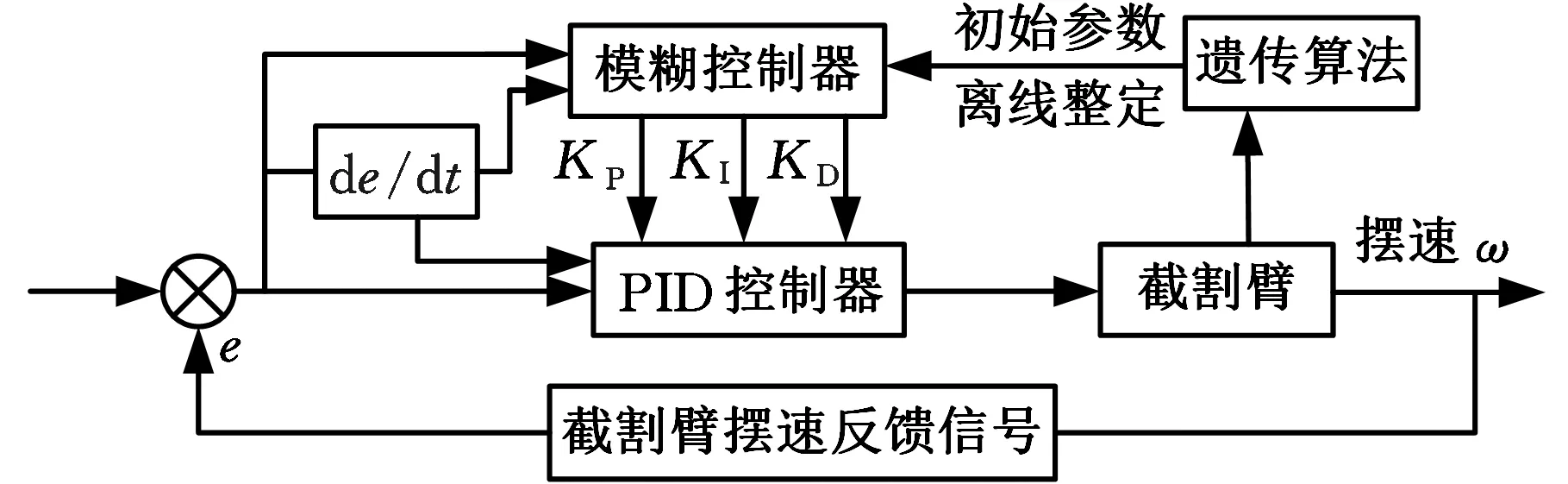
图6 GA-FPID控制器结构Fig.6 Structure of GA-FPID controller

4.1 模糊控制器设计

模糊控制器的设计原则是使掘进机可根据煤岩状态高效自适应截割，针对截割臂摆速控制系统并依据模糊逻辑理论设计了一种二维模糊控制器。二维模糊控制器以RBF载荷识别器输出信号与掘进机摆速反馈信号的偏差e及偏差变化率ec作为输入，以PID控制参数KP、KI、KD为输出。输入与输出模糊子集设定为：{NB，NM，NS，Z，PS，PM，PB}={负大，负中，负小，零，正小，正中，正大}，输入项e的模糊控制器隶属函数图形如图7所示,其他项隶属函数图形与之相同[15]。

图7 输入项e的隶属函数示意图Fig.7 Membership function diagram of input item e

模糊推理选择Mamdani法，模糊判决选择重心法。因输入输出项模糊子集均采用7个隶属函数，故共设定49条模糊规则，总结制定模糊规则如表3所示。

4.2 遗传算法设计

遗传算法主要包括编码规则、适应度函数、遗传算子、运行参数4个主要要素，针对掘进机截割臂摆速控制系统，采用遗传算法原理对PID初始控制参数及模糊控制器比例因子的寻优过程如下[16]：

(1)分别确定PID控制参数KP、KI、KD取值范围与模糊控制器量化比例因子KP、KI、KD取值范围，并设定种群规模50、进化代数50、交叉概率0.9、变异概率0.1、求解精度0.01等遗传算法相关运行参数。

表3 模糊规则表

(2)创建KP、KI、KD与KP、KI、KD初始种群，并采用二进制编码规则对其进行编码与解码。

(3)适应度函数作为种群的评价指标，是影响优化效果的关键因素，在权衡控制系统稳定性、准确性及快速性等方面控制因素，本文确定适应度函数为

(9)

式中，Es为系统稳态误差;Mp为超调量;Tr为上升时间。

(4)依据适应度函数计算截割臂摆速控制系统每代种群个体适应度值，最后根据适应度值对个体进行选择、单点交叉、双点交叉、变异等遗传操作，从而产生新一代种群。

(5)重复步骤(4)，直至满足设定目标，输出最优值。

根据上述过程在MATLAB软件中分别编写遗传算法寻找PID最优控制参数程序和遗传算法寻找模糊控制器最优量化比例因子程序，运行得到截割臂控制系统PID控制参数KP、KI、KD的最优值为1.94、181.46、0.07，迭代过程如图8所示，模糊控制器量化比例因子KP、KI、KD最优值为1.04、9.46、0.088，迭代过程如图9所示。

图8 PID控制参数寻优过程Fig.8 PID control parameters optimization process

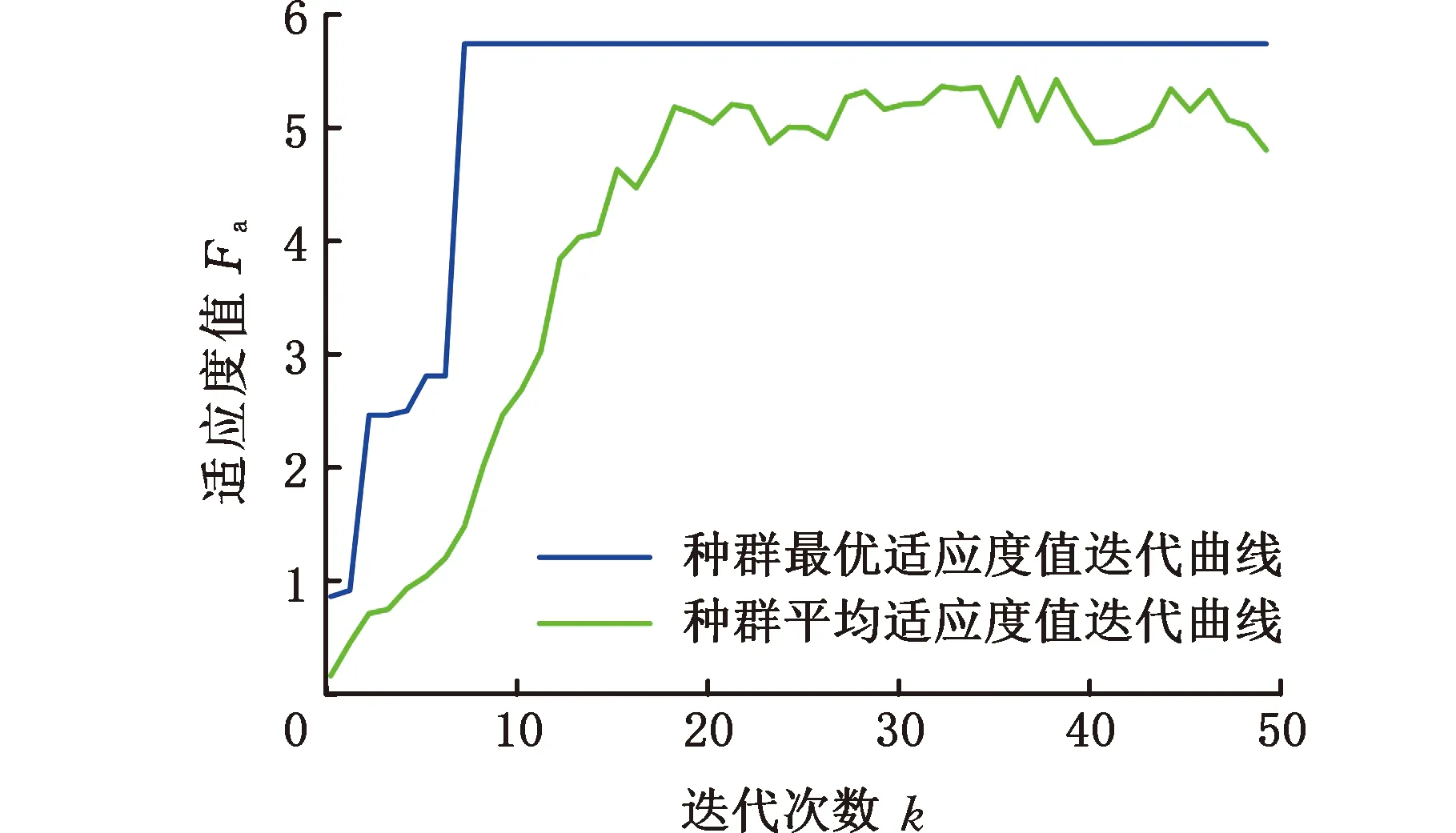
图9 量化比例因子寻优过程Fig.9 Quantitative scaling factor optimization process

5 截割臂自适应截割控制系统仿真分析

5.1 仿真控制系统建模

根据上文提出的截割臂自适应截割控制策略，基于Simulink建模仿真方法，建立掘进机截割臂自适应截割仿真控制系统。仿真控制系统由RBF载荷识别控制器、载荷与摆速转换环节、GA-FPID控制器、比例放大器、电液比例阀，液压缸、液压缸行程与摆角位移转换环节等部分组成，其中RBF载荷识别控制器直接封装为Simulink模块，GA-FPID控制器通过编写程序导入Simulink模块，对截割臂控制系统分别建立数学模型及传递函数。

载荷与摆速转换环节中，当神经网络载荷识别器识别到{I，p，a}信号在割煤工况范围时，截割载荷输出F恒为0，截割臂始终以最大速度ωmax截割；当输入信号在硬岩工况范围时，截割载荷输出F恒为1，截割臂摆速降为0，截割头破碎硬岩后再继续进给；当输入信号在煤岩夹杂工况范围时，截割载荷信号F输出为0～1，神经网络输出载荷信号越大，期望摆速越小；根据以上分析建立载荷与摆速转换环节传递函数：

ω′=ωmax(1-F)

(10)

式中，ω′为截割臂期望摆速；ωmax为截割臂最大摆速。

比例放大器是电液比例阀的驱动装置，它对控制器输出的信号进行放大、转化，并输出电流信号，从而对电液比例阀进行控制，其数学模型为

(11)

式中，Ka为比例放大器增益。

电液比例方向阀数学模型可简化为二阶振荡环节，其传递函数为

(12)

式中，Kq为电液比例阀流量增益；ωv为换向阀系统固有频率；δv为换向阀系统阻尼比；QV为阀输出流量。

液压缸系统传递函数为

(13)

式中，A为无杆腔有效作用面积；ωh为液压缸系统固有频率；δh为液压缸系统阻尼比；L为液压缸活塞杆行程。

液压缸行程与截割臂摆角位移转换环节可近似为比例环节，其传递函数为

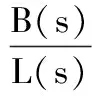
(14)

式中，Kb为活塞杆行程与悬臂摆角增益；B为悬臂摆角位移[17]。

根据式(8)～式(12)，以及RBF载荷识别器模块、GA-FPID控制器模块，在Simulink中建立截割臂自适应截割仿真控制系统，如图10所示。

图10 自适应仿真控制系统框图Fig.10 Block diagram of adaptive simulation control system

5.2 仿真分析

以石家庄煤矿机械公司生产的EBZ135型掘进机为例，根据截割臂各部件技术参数及相关文献[18-19]开展仿真研究，仿真控制系统各环节参数如表4所示。

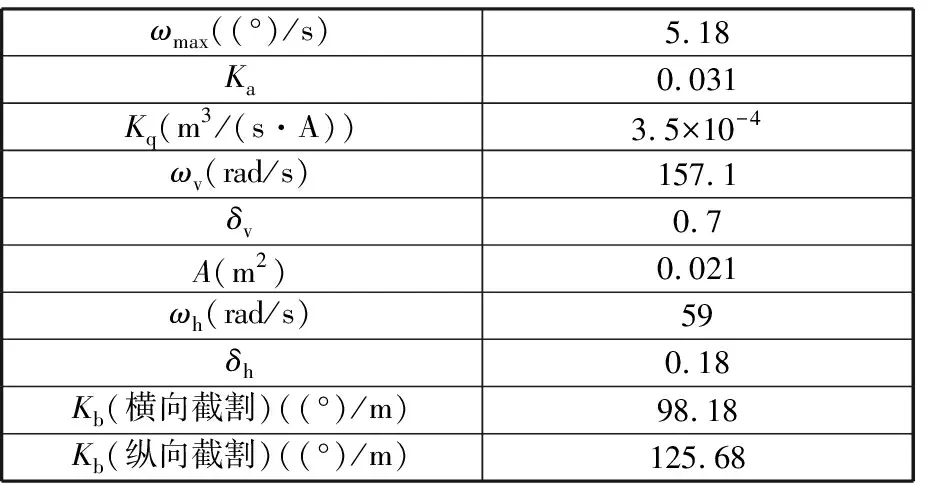
表4 仿真系统参数

选取不同工况下截割载荷信号{I，p，a}输入到截割臂自适应截割控制系统进行仿真分析，并与传统PID控制效果进行仿真对比，割煤工况下截割臂摆速仿真结果如图11所示，煤岩夹杂工况下不同截割载荷信号的截割臂摆速控制仿真结果如图12所示。由仿真结果可得，当识别到截割载荷信号处于割煤工况时，截割臂调整到最大摆速掘进；当处于煤岩夹杂及硬岩工况时，掘进机根据截割载荷信号对截割臂进行自适应调速，截割载荷信号较小时，截割臂摆速增大，截割载荷信号较大时，截割臂摆速降低。由截割臂摆速仿真效果可得，GA-FPID控制器在不同的截割状态信号变化下相比PID控制响应速度更快、控制精度更高。仿真结果表明:当煤岩硬度发生变化时，掘进机控制系统可依据截割载荷信号变化对摆速进行精准快速调控，实现截割臂依据截割载荷信号的自适应截割。

图11 割煤工况下摆速控制仿真结果Fig.11 Simulation results of swing speed controlunder coal cutting condition

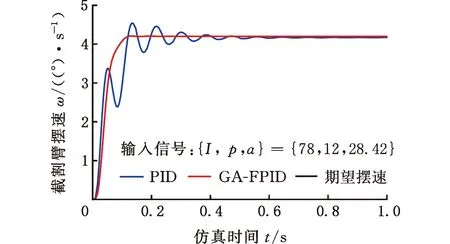
(a)截割载荷信号较小时摆速控制结果

(b)截割载荷信号较大时摆速控制结果图12 煤岩夹杂工况摆速控制仿真结果Fig.12 Simulation results of pendulum speed control

6 验证性实验

6.1 实验方案

为验证本文提出的掘进机截割臂自适应截割控制策略的有效性，基于课题组搭建的掘进机远程智能控制实验平台(图13)进行了掘进机截割臂自适应截割控制实验。实验地点为石家庄煤矿机械有限公司的模拟巷道，实验机型为EBZ135型掘进机。

图13 截割臂自适应截割实验平台Fig.13 Cutting arm adaptive cutting experimental platform

实验步骤如下：

(1)采用贝加莱Automation Studio软件对机载自适应截割控制系统包含的RBF神经网络载荷识别器、遗传算法优化的模糊PID控制器及各状态参数进行配置、编程、监测、诊断。

(2)将课题组前期实测的井下多传感器信息数据组作为截割载荷信号模拟量输入到上位机中，模拟掘进机井下掘进过程中实际截割工况。

(3)经神经网络载荷识别器输出截割载荷信号到下位机中，PCC下位机根据截割载荷信号控制电液系统自动调节截割臂摆速。

(4)通过摆角传感器测取摆角变化来得到截割臂摆速变化过程，通过机载状态传感器监测截割电机电流与电压得到截割电机功率变化过程。实验原理如图14所示。

图14 实验原理图Fig.14 Experimental principle

实验选用本质安全型GUC360矿用倾角传感器测取截割臂垂直摆角变化，选用稳定性好、抗干扰能力强的W18LD型双路测速传感器测取截割臂的水平摆角变化。测取截割臂的水平摆角时，根据截割臂回转台结构，在回转台内侧一定弧长范围内安装两个齿条，其中一个齿条不动，另一个跟随回转台转动，将双路测速传感器对准齿条，作用距离0～2 mm，每经过一个齿条宽度4 mm，对应的截割臂摆动为1°，随着截割臂摆动，双路测速传感器就可直接输出水平摆角变化信号。

6.2 实验结果

每间隔10 s输入不同截割工况下的多传感器数据组{I，p，a}，利用贝加莱Automation Studio软件记录截割载荷信号变化、截割臂摆速变化及截割功率变化过程，实验过程与结果如图15所示。

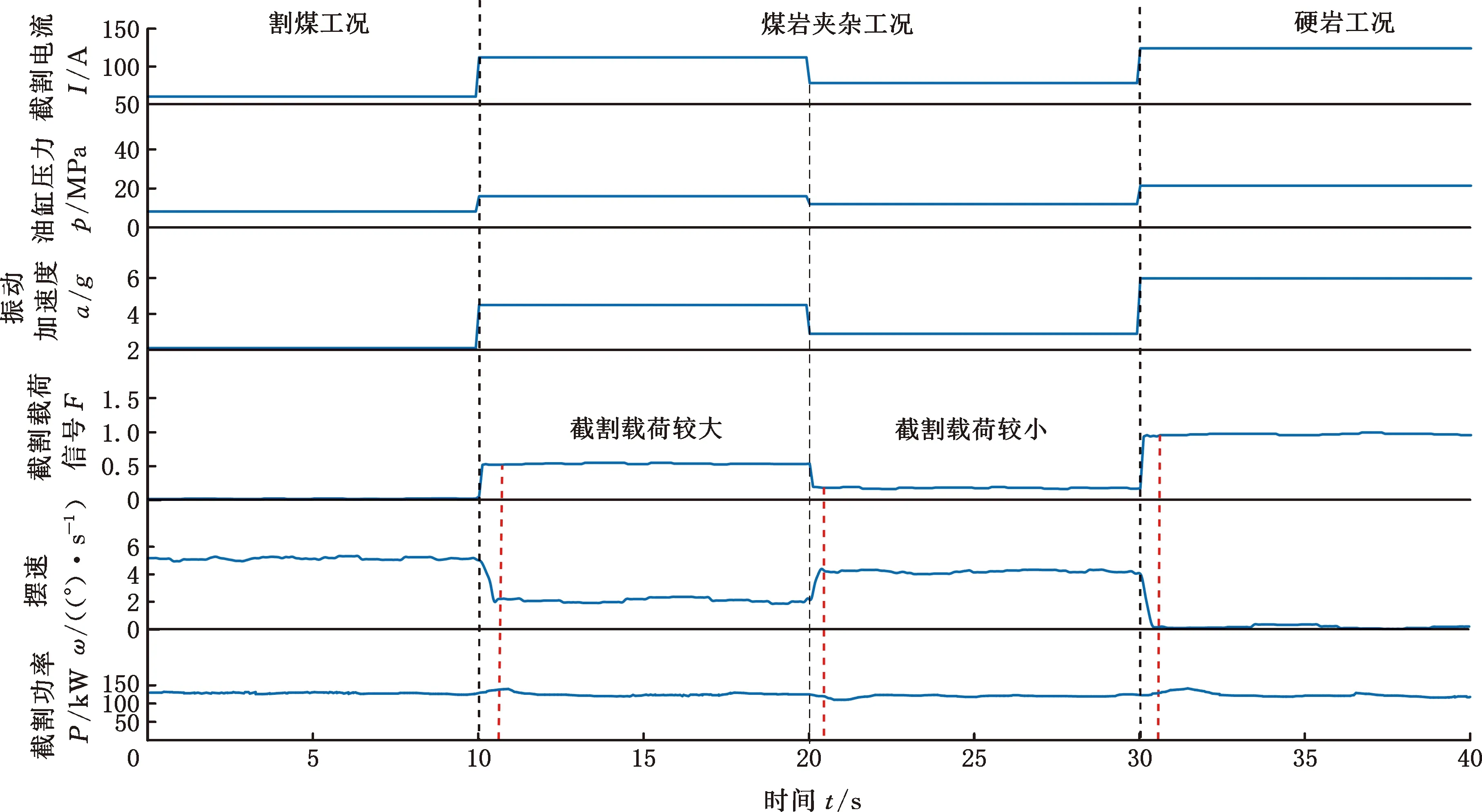
图15 模拟截割实验过程与结果Fig.15 Process and results of simulated cutting experiment

由实验结果可得，当输入多传感器数据组信号{I，p，a}为割煤工况时，截割载荷信号输出为0，截割臂以最大摆速截割；当输入{I，p，a}信号为煤岩夹杂工况时，截割载荷信号在0～1之间，截割臂根据截割载荷信号大小自适应截割；当输入{I，p，a}信号为硬岩工况时，截割载荷信号输出为1，截割臂摆速降为0；实验过程中截割电机功率稳定在额定功率135 kW上下。截割载荷信号识别误差与摆速调节误差曲线如图16所示。

图16 截割载荷信号识别误差与摆速调节误差曲线Fig.16 Curve of cutting load signal identification errorand swing speed adjustment error

由误差曲线可得，实验中RBF神经网络识别截割载荷信号最大绝对误差小于0.05，平均误差小于1×10-3，与前期测试误差相符；截割臂摆速调节最大误差小于0.3°/s，平均误差小于1×10-2，满足井下使用要求。实验证明本文提出的基于多传感器信息的GA-FPID自适应截割控制系统可以实现对截割臂摆速的自适应调控。

7 结论

(1)提出了一种基于多传感器信息的掘进机截割臂自适应截割控制策略。基于井下实测数据设计了一种RBF神经网络载荷识别控制器，载荷信号识别训练与测试精度可达1×10-3。针对复杂且时变的截割臂摆速控制系统，设计了一种基于遗传算法优化的模糊PID智能控制器，在Simulink中建立了截割臂摆速自适应控制仿真系统，仿真结果表明，基于多种传感器信息的GA-FPID控制系统可实现截割臂摆速的快速自适应调控。

(2)在石家庄煤矿机械有限公司模拟巷道中使用EBZ135型掘进机进行了模拟自适应截割实验，实验结果验证了该控制策略的有效性，实现掘进机截割臂依据截割状态参数的变化进行高效自适应调速，满足井下掘进机智能截割的需求。

(3)本文提出的基于多传感器信息掘进机截割臂自适应截割控制策略有助于推进煤矿井下掘进设备的智能化和机器人化，为少人化掘进工作面的建立奠定了基础，有助于延长井下掘进设备使用寿命、提高巷道掘进效率。