Hamiltonian Bi-integrable Couplings for the Counterpart of the AKNS Soliton Hierarchy

WANG Lei(王蕾) ,TANG Yaning(唐亚宁)

(1.School of Mathematics and Statistics,Taiyuan Normal University,Jinzhong 030619,China;2.School of Mathematics and Statistics,Northwestern Polytechnical University,Xi’an 710129,China)

Abstract:Based on zero curvature equations from semi-direct sums of Lie algebras,we construct bi-integrable couplings for the counterpart of the AKNS soliton hierarchy and their Hamiltonian structures by applying a class of non-semisimple matrix loop algebras consisting of triangular block matrices.

Key words:Semi-direct sums of Lie algebras;Zero curvature equation;Bi-integrable coupling;Hamiltonian structure

1.Introduction

Integrable Hamiltonian systems are the important contents in soliton theory.Many typical integrable Hamiltonian hierarchies with physics backgrounds,appeared based on the powerful approach of the loop algebra under the framework of the zero curvature equation developed by TU[1].

For a given integrable system:

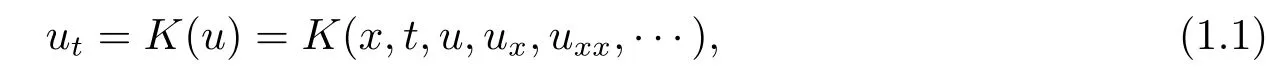
if we can construct a new triangular integrable system as follows[2]:

whereuandvdenote two column vectors of additional dependent variables,then we call(1.2)is an integrable coupling of the system (1.1).

A bigger triangular integrable system than (1.2) of the form

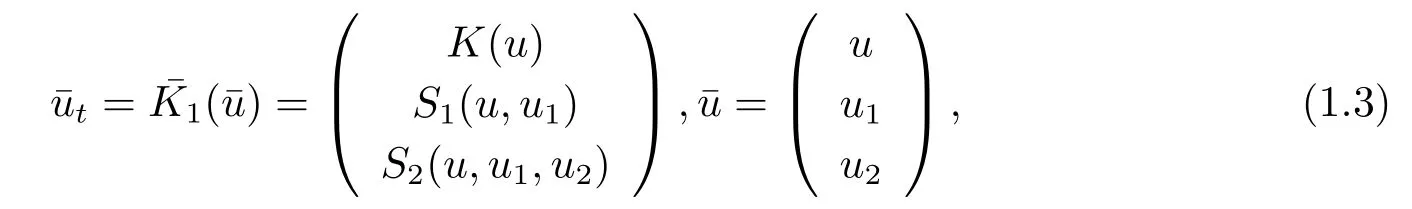
is called a bi-integrable coupling[3]of the system (1.1).Recently,various examples of biintegrable couplings were introduced,which give complements the members of integrable systems and bring more interesting studies to the theory of integrable systems.

The paper is organized as follows.In Section 2,we will introduce the counterpart of the AKNS soliton hierarchy.In Section 3,we will generate a kind of bi-integrable couplings for the counterpart of the AKNS soliton hierarchy and their Hamiltonian structures.In Section 4,conclusions will be given.

2.A Counterpart of the AKNS Soliton Hierarchy

We introduce the counterpart of the AKNS soliton hierarchy as follows[4]:

whereλis the spectral parameter,p,qare two dependent variables.Upon setting[5]

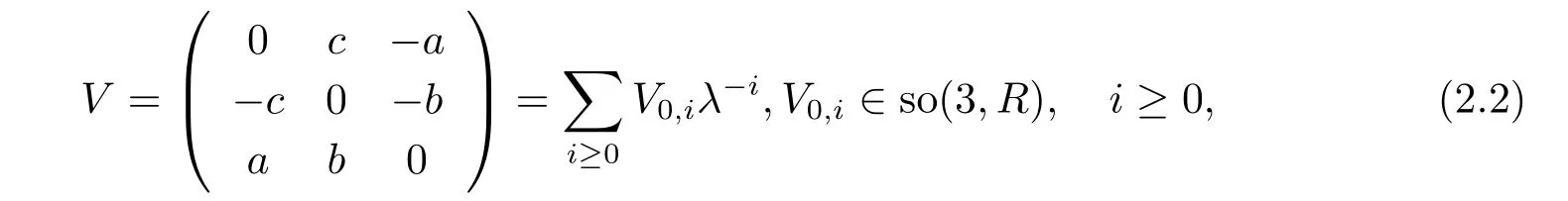
and the stationary zero curvature equationVx=[U,V],we can generate

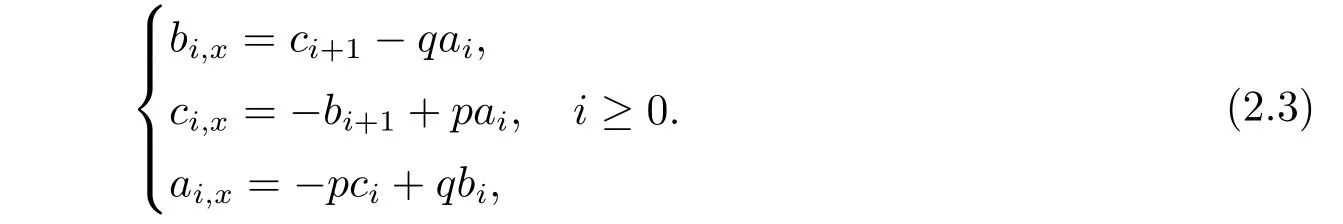
Using the compatibility conditions

3.Hamiltonian Bi-integrable Couplings for the Counterpart of the AKNS Soliton Hierarchy

We will use a non-semisimple matrix loop algebra consisting of 3×3 block matrices,and a class of zero curvature equations over this loop algebra presented in [6] to generate a class of bi-integrable couplings[7-8]for the counterpart hierarchy (2.5).

Ⅰ Bi-integrable couplings

Ⅱ Hamiltonian structures of the bi-integrable couplings

In order to generate Hamiltonian structures for the bi-integrable couplings (3.13),we apply the variational identity[7,9]:

whereη1,η2andη3are arbitrary constants.So a bilinear form on the semi-direct sumis given by

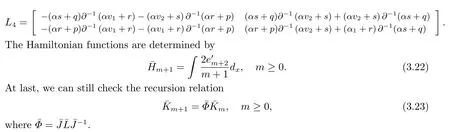
The counterpart of the AKNS soliton hierarchy (2.5) is a new soliton hierarchy.The results in (2.1) and (2.5) are different from the AKNS soliton hierarchy (3.18) and (3.25) in[8].We remark that the results in (3.13) and (3.19)-(3.20) are different from the results in(3.39) and (3.45)-(3.46) in [8],which were obtained by using a different class of matrix Lie algebra,and we generate the recursion operatorin (3.21).

4.Conclusions

In this paper,bi-integrable couplings of the counterpart of the AKNS soliton hierarchy were obtained by applying a kind of matrix loop algebras.Meanwhile,Hamiltonian structures of the resulting bi-integrable couplings were established through the variational identity on the adopted matrix loop algebras.Our methods used in this paper will be able to be applied to other different integrable hierarchies,and we can study their Hamiltonian tri-integrable couplings.

Furthermore,the solution of the soliton equation is also very important,numerous researchers have contributed themselves to finding the exact solutions.In the future,we will use the methods in [12-15] to study the exact solution of the soliton equation,for example,multi-soliton solution,rational solution,lump solution,interaction solution and so on.