基于多中继线圈结构的无线电能传输系统恒流/恒压输出方法
陈永洪,黎祎阳,杨 斌,陈 阳,麦瑞坤
(西南交通大学电气工程学院,四川省成都市 611756)
0 引言
高压杆塔上的在线监测设备(online monitoring equipment,OME)可以提供大量有用的输电线路状态数据[1-2],是电力系统实现信息化和现代化的必要组成部分。当前常用的供电方式为:使用电流互感器从输电线路中采集电能[3],然后将其传输给OME。但是电力系统可能产生断路故障,因此有必要给OME 安装蓄电池,以提供稳定的电能[1,4]。采集到的能量需要从高压侧传输到低压侧,因此绝缘安全是关键考虑因素。基于多中继线圈的无线电能传输(wireless power transfer,WPT)系统(以下简称“多中继WPT 系统”),可以跨越绝缘距离,安全地为OME 充电[5-7]。
当前,采用多中继WPT 系统给OME 中的锂电池充电的方式主要是恒流[8](constant current,CC)或恒压(constant voltage,CV)充电[9-10]。恒流充电虽然速度快,但是电池容易过充爆炸;恒压充电虽然安全性高,但是充电初期的大电流会损伤电池[11]。综合考虑充电安全与速度,主流的锂电池充电方式为恒流/恒压充电,即先对负载进行恒流充电,当负载电压升高到额定电压时,再切换到恒压充电,直至充电过程结束。实现恒流/恒压充电的方式有3 类:1)采用控制的方法,主要是对逆变器进行变频、移相控制,或者通过控制前、后级DC/DC 变换器来控制输出[12];2)通过开关切换来实现恒流拓扑到恒压拓扑的切换[13-15];3)通过切换系统工作频率来实现从恒流模式到恒压模式的切换[16-18]。其中,切换系统工作频率的方式由于未引入额外的元件,最大程度减少了元件数量,降低了成本。同时,还避免了DC/DC 变换器或额外交流开关而带来的多余功率损耗,是目前实现恒流/恒压输出的较好方式。利用这种改变工作频率来实现恒流到恒压切换的多中继WPT 系统,可简单、快速和安全地为OME 充电。然而,多中继线圈之间复杂的交叉耦合增大了实现恒流/恒压输出的难度。
目前,对多中继线圈实现恒流/恒压输出的研究还较少。文献[6,19]为了简化分析,将每一个电流回路都设置为谐振状态,这使得如果不外加控制,就只能实现恒流或者恒压输出,而不能兼得。文献[8]将多中继WPT 系统等效成一个串联-串联(SS)拓扑,实现了恒流且零相角(zero phase angle,ZPA)输出,但是未对恒压输出作讨论。文献[20]从特征值的角度分析了多中继WPT 系统的输出特性,但是并未给出电流增益、电压增益与系统参数之间的详细关系,也未给出多中继WPT 系统的参数设计流程,并且所建立的理论模型较为抽象和复杂。文献[4]基于12 个线圈的多中继WPT 系统,其前11 个线圈所在电流回路为S 拓扑,最后一个线圈所在回路为S 拓扑+LCC 拓扑的混合拓扑。然后,通过数值计算,获得了该系统的工作频率和补偿参数,最后通过控制额外交流开关的导通与关断,将系统从恒流拓扑切换到恒压拓扑,从而实现恒流/恒压输出。然而,该设计方法未涉及工作频率、输入阻抗与系统参数之间的内在关系,导致很难对多中继WPT 系统做更进一步的分析,且通过开关切换拓扑从而实现恒流/恒压输出的方式,在一定程度上增加了系统结构的复杂度。
本文分析并获得了系统系数矩阵及其子矩阵的行列式与恒流、恒压的频率和增益之间的简单定量关系,并对具体的多中继WPT 系统做了详细的分析,提出了在存在复杂交叉耦合的多中继线圈结构中,通过切换系统工作频率来实现恒流/恒压输出的方法。
1 多中继WPT 系统理论建模

基于基尔霍夫电压定律,对图1 所示的多中继WPT 系统列写网孔电流方程[21]:
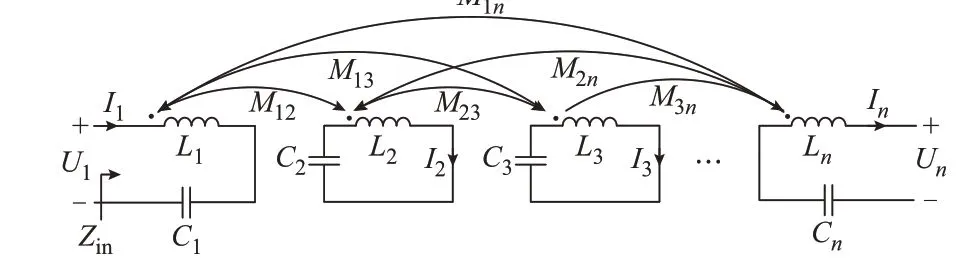
图1 n 线圈多中继WPT 系统电路拓扑图Fig.1 Circuit topology of n-coil multi-relay WPT system
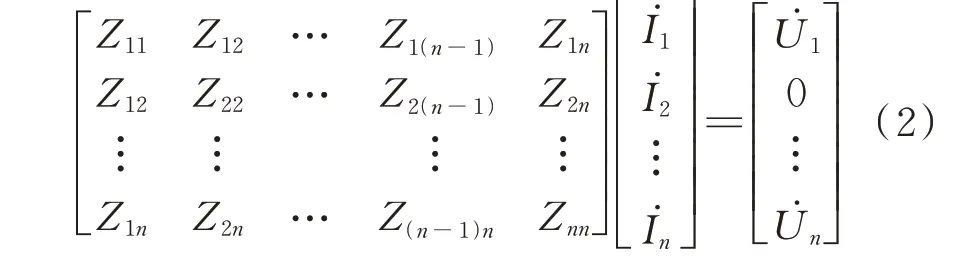
式中:Zii(i=1,2,…,n)为每个回路的自阻抗;Zij(i=1,2,…,n且j=i+1,i+2,…,n)为第i个和第j个回路之间的互阻抗。
Zii和Zij的表达式分别为:
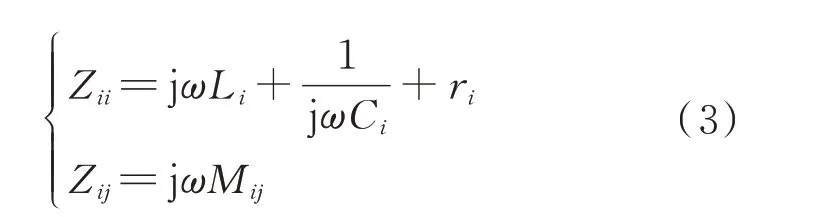
式 中:ω= 2πf为 角 频 率,其 中,f为 频 率;ri(i=1,2,…,n)为由线圈的交流内阻、电容的寄生电阻、线路内阻所组成的串联等效电阻(equivalent series resistance,ESR)值。
利用分块矩阵理论求解式(2)可得[22]:

图1 为含有n个线圈的多中继WPT 系统,其中:U1和Un分别为输入电压相量U̇1和输出电压相量U̇n的基波有效值;Mij、Li、Ci(i=1,2,…,n且j=i,i+1,i+2,…,n)分别为互感、自感和补偿电容;Ii(i=1,2,…,n)为 第i个 回 路 的 电 流 相 量İi的 有 效值;Zin为输入阻抗,其值如式(1)所示。
定 义H0,n、H1,n、H2,n、H3,n、H4,n分 别 为n线 圈WPT 系统的恒压行列式、恒流行列式、恒流ZPA 行列式、恒压ZPA 行列式和增益行列式。
联立式(1)、式(4)和式(5)可得:
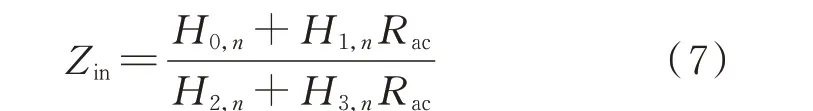
式中:Rac为交流等效电阻,其值为U̇n与İn的比值。
如果不考虑ESR,那么Zii和Zij均为纯电抗,其实部Re(Zii)和Re(Zij)均为零,则由纯电抗组成的方阵有如下规律:
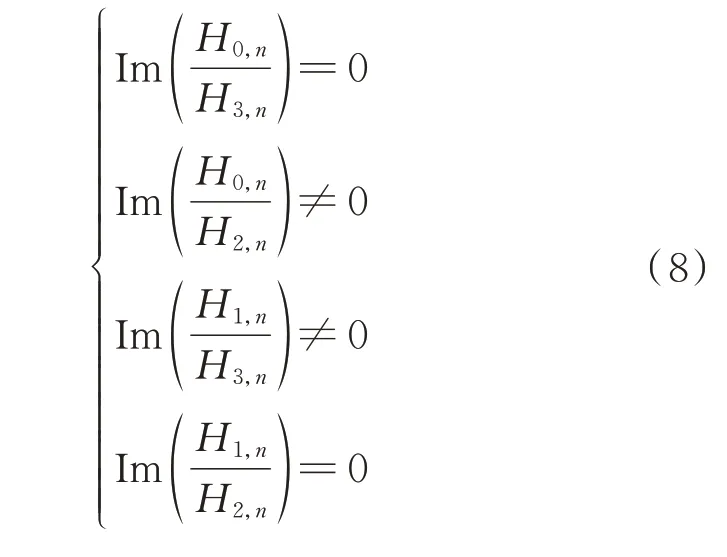
式(8)的证明过程见附录A。
根据式(4)—式(8)即可推导出多中继WPT 系统的恒流/恒压输出模型。
1)恒流模式分析
由于系统的激励为恒压源,因此式(4)中的U̇1恒定。所以,恒流行列式H1,n=0(定义该方程为恒流方程)是实现恒流输出的充要条件。将H1,n=0 代入式(7)可得:
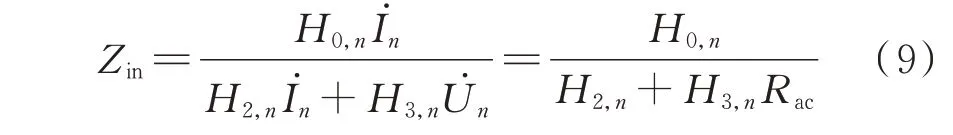
根据式(8)可知,式(9)中的恒流ZPA 行列式H2,n=0(定义该方程为恒流ZPA 方程)是此时实现ZPA 的充要条件。将H1,n=0 代入式(4),则恒流模式中的交流电流增益Gac,cc如式(10)所示,并定义该式为恒流增益方程。
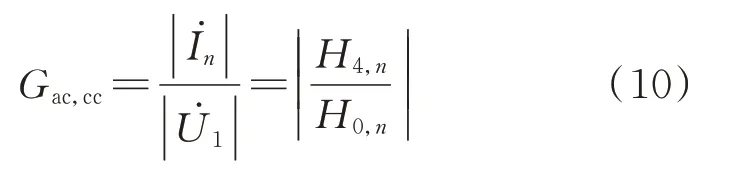
式中:|·|表示取复数的模长。
2)恒压模式分析
由式(4)可得实现恒压输出的条件为恒压行列式H0,n=0(定义该方程为恒压方程),将H0,n=0 代入式(7)并根据式(8)可得,ZPA 行列式H3,n=0(定义该方程为恒压ZPA 方程)是此时实现ZPA 的充要条件。此时的交流电压增益Gac,cv见式(11),并定义该式为恒压增益方程。
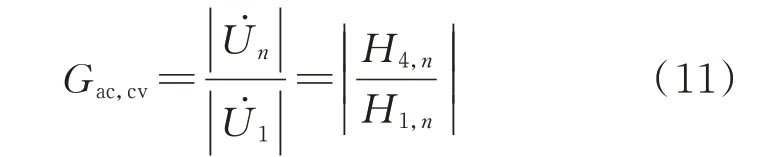
综合上述分析可知,多中继WPT 系统实现恒流 且ZPA 输 出 的 条 件 是H1,n=0 且H2,n=0,此 时 的电流增益为式(10);实现恒压且ZPA 输出的条件是H0,n=0 且H3,n=0,此时的电压增益为式(11)。这6 个方程完整描述了多中继WPT 系统的恒流、恒压输出特性。
2 四线圈多中继WPT 系统分析
2.1 系统建模
令第1 章中的n为4,设计了一套四线圈多中继WPT 系统,其电路拓扑见附录B 图B1(a),电磁耦合机构见图B1(b)。图B1(a)中E为直流输入电压,Uo和Io分别为负载Ro的电压和电流。交流输出电压和交流输出电流的基波有效值分别为U4和I4。
全桥逆变器和全桥不控整流的输入与输出之间有以下关系[23-24]:
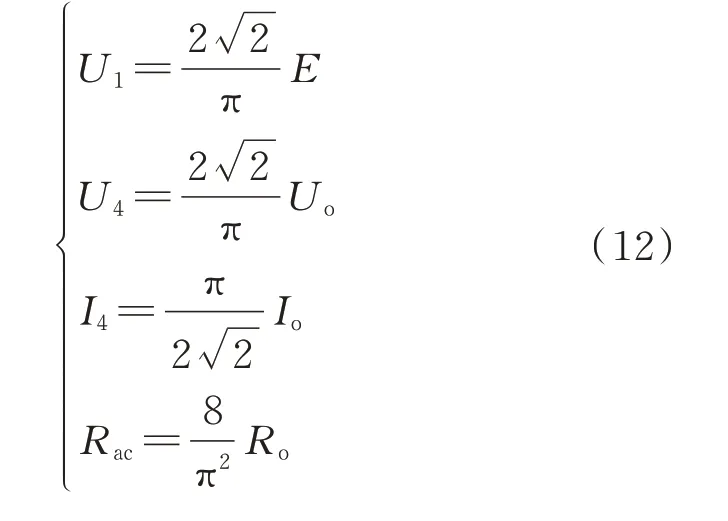
1)恒流模式
令式(3)中的ω=ωcc(ωcc为恒流模式的工作角频率),则此时的恒流方程和恒流ZPA 方程分别为式(13)和式(14),该四线圈系统恒流模式中的电流增益Gcc的表达式即恒流增益方程见式(15)。

式中:Zccii、Zccij(i=1,2,3,4;j=i,i+1,…,4)分别为恒流模式中第i个回路的自阻抗和第i个回路与第j个回路之间的互阻抗。
式(13)使系统实现恒流输出,式(13)和式(14)共同作用使系统实现ZPA 输出。
2)恒压模式
令式(3)中的ω=ωcv(ωcv为恒压模式的工作角频率),则此时的恒压方程和恒压ZPA 方程分别为式(18)和式(19),该四线圈系统恒压模式中的电压增益Gcv的表达式即恒压增益方程见式(20)。
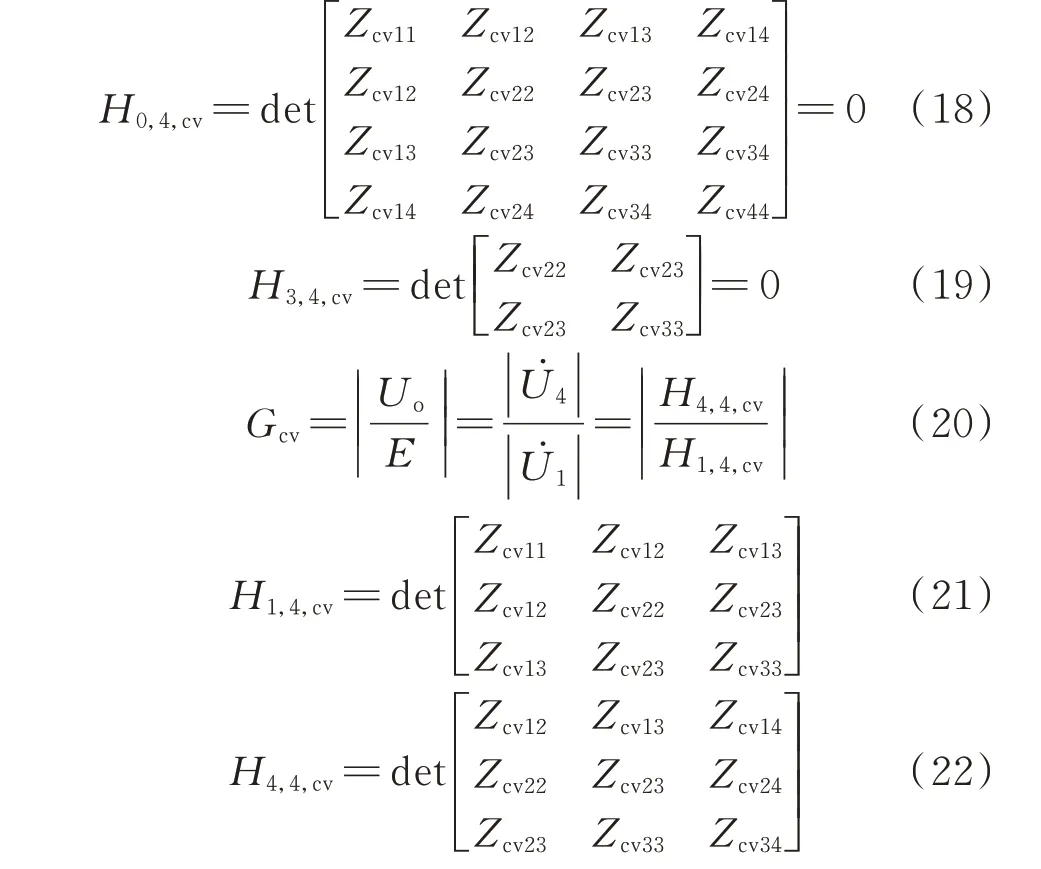
式中:Zcvii、Zcvij(i=1,2,3,4;j=i,i+1,…,4)分别为恒压模式中第i个回路的自阻抗和第i个回路与第j个回路之间的互阻抗。
式(18)使系统实现恒压输出,式(18)和式(19)共同作用使系统实现ZPA 输出。
2.2 参数设计
在确定了线圈参数和输出增益后,四线圈多中继WPT 系统还有6 个未知数待解,分别是4 个补偿电容、恒流频率和恒压频率。通过第1 章中的分析可知,通过联立求解恒流方程、恒压方程、恒流ZPA方程、恒压ZPA 方程、恒流增益方程和恒压增益方程即可求出这6 个未知数。然而,直接求解计算量太大,于是利用数据分析软件(Wolfram Mathematica),采用参数迭代的方式来简化求解过程。四线圈多中继WPT 系统的参数设计流程见图2。当线圈个数超过4 时,设计流程见附录C图C1。
通过有限元仿真软件Maxwell 和图2 所示迭代算法,为四线圈多中继WPT 系统设计了一套如附录B 表B1 所示的参数,其中Gcc为0.03,Gcv为0.6。
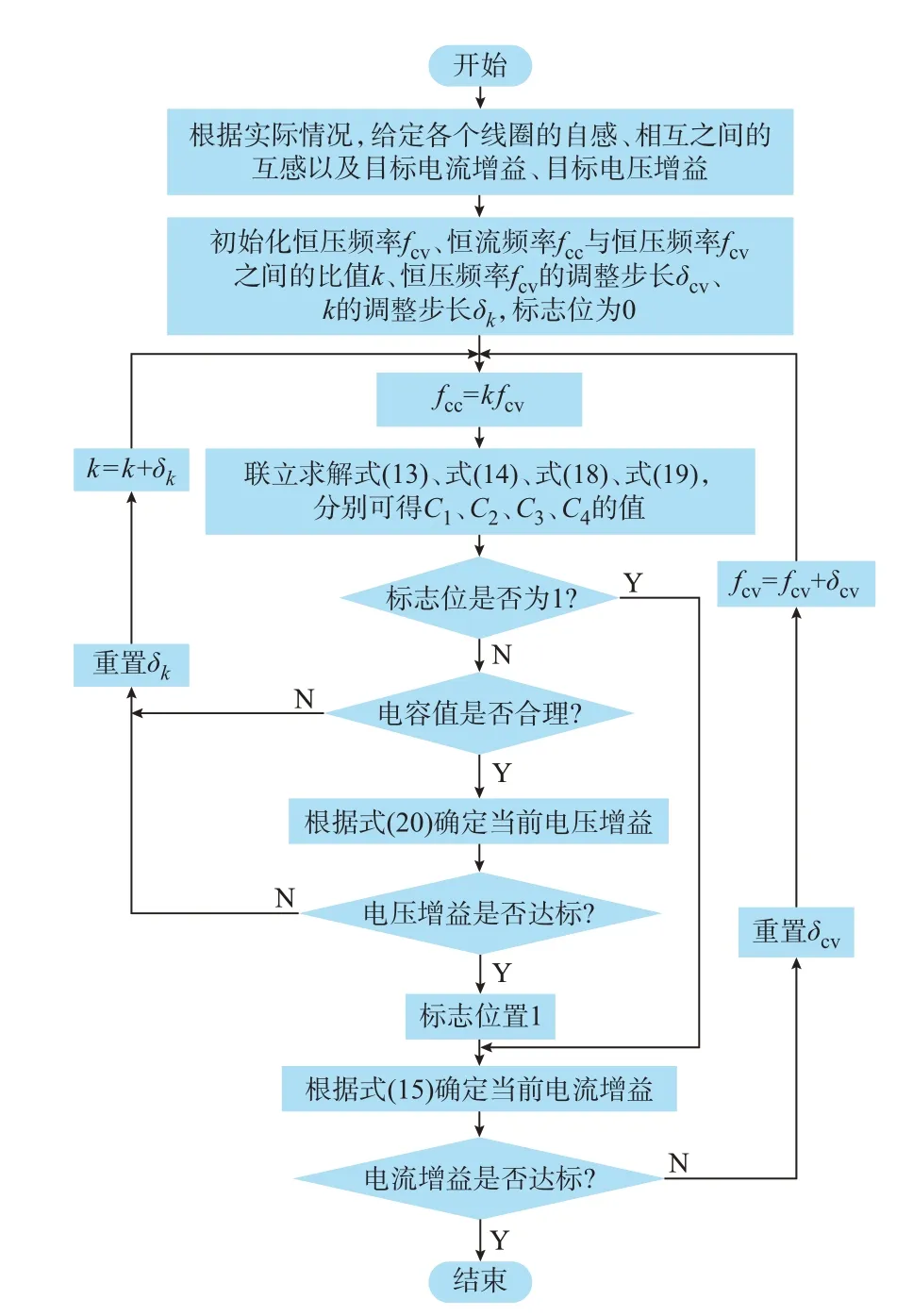
图2 四线圈多中继WPT 系统参数设计流程Fig.2 Parameter design process of four-coil multi-relay WPT system
2.3 特性分析
由式(4)可知,四线圈多中继WPT 系统的输入与输出之间的关系为:
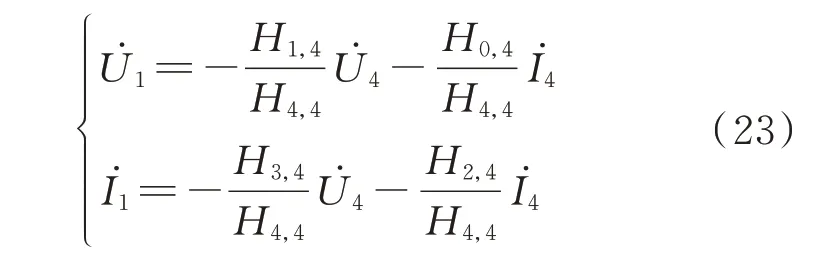
根据式(23)可知,电流增益Gcc和电压增益Gcv分别为:
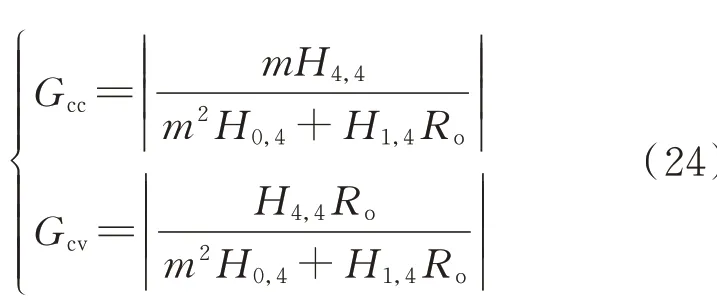
式中:m=π2/8。
由式(7)可得,四线圈多中继WPT 系统的输入阻抗Zin及输入阻抗角θ分别为:
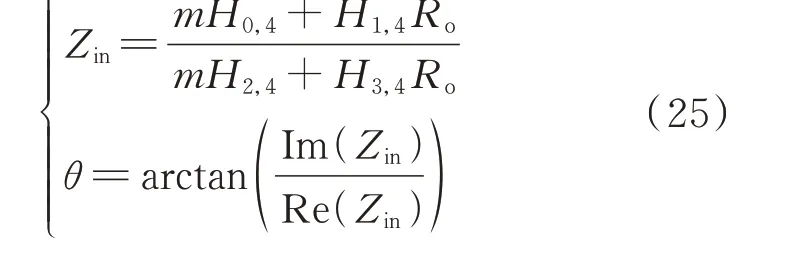
频率特性是多中继WPT 系统的重要特性,根据附录B 表B1 中的参数、恒流行列式、恒压行列式、式(24)和式(25),可绘制出图3 所示的四线圈多中继WPT 系统的频率特性曲线,其中CC1、CC2分别表 示 第1 个 和 第2 个 恒 流 点,ZPA1、ZPA2分 别 表示 第1 个和第2 个ZPA 点,CV1、CV2、CV3、CV4表示第1 至4 个恒压点。
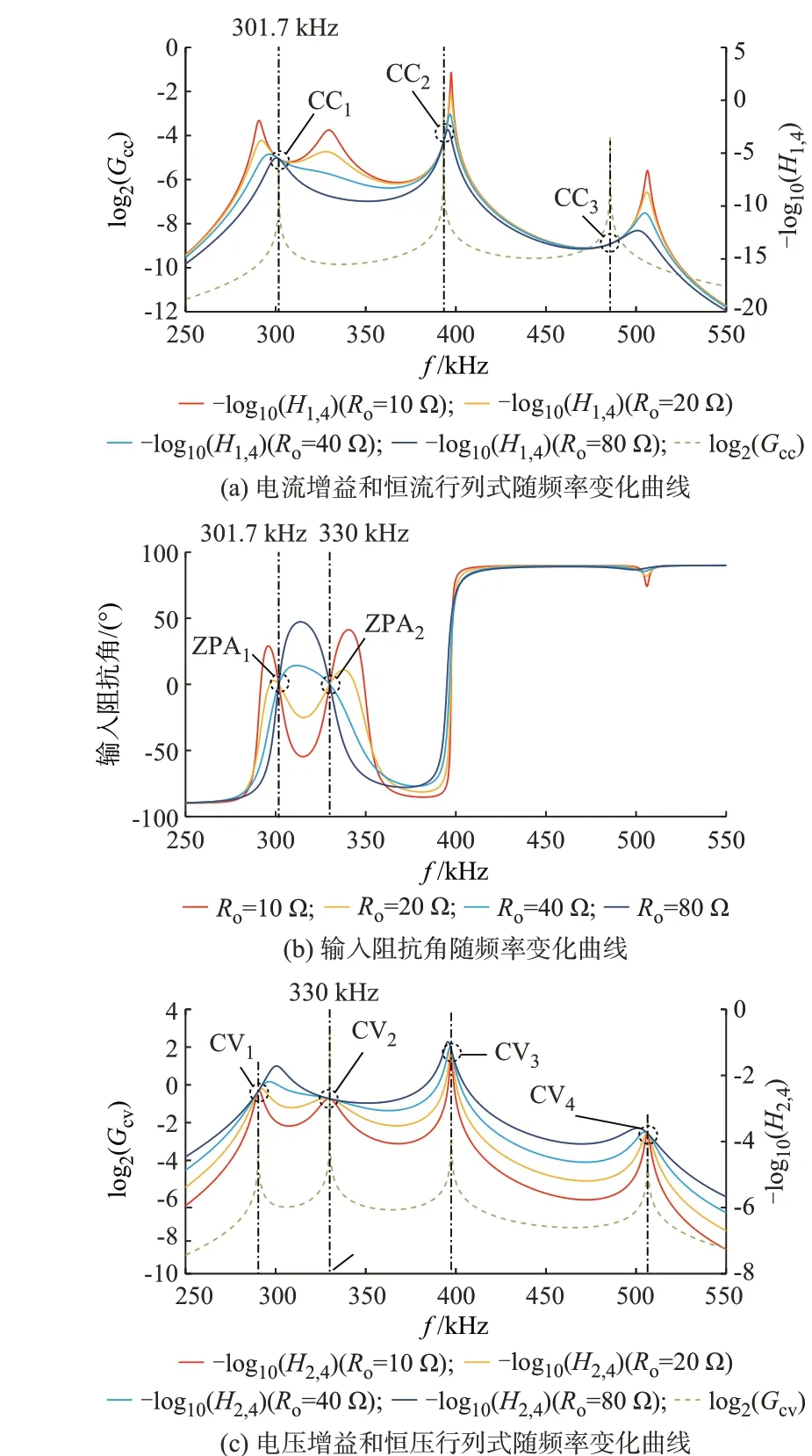
图3 四线圈多中继WPT 系统频率特性曲线Fig.3 Frequency characteristic curves of four-coil multi-relay WPT system
由第1 章中的分析可知,求解恒流方程H1,4=0可得所有的恒流频率点,此时的H1,4为频率f的函数,记为H1,4(f)。由式(3)、式(6)可知,H1,4(f)=0是一个形如a1f6+a2f4+a3f2+b=0(a1、a2、a3和b均为复数且a1≠0)的一元六次方程,根据代数基本定理,该方程在复数域内有6 个根。 令function(f)=a1f6+a2f4+a3f2+b, 由 于function(f)=function(-f),所 以function(f)是 一个偶函数,其若存在零点,则关于原点中心对称。因此,在正实数域内,H1,4(f)=0 至 多有3 个根,即四线圈多中继WPT 系统至多有3 个恒流频率点。图3(a)展示了3 个不同负载下的增益-频率曲线交点的横坐标,即3 个恒流频率点,正好对应函数-log10(H1,4(f))曲 线 的3 个 无 穷 间 断 点,即 恒 流 方程H1,4(f)=0 的3 个根。同理,恒压方程H0,4(f)=0是 一 个 形 如a1f8+a2f6+a3f4+a4f2+b=0(a1≠0)的一元八次方程,如果这个方程的根全为实数,则有4 个根分布在正实数域内,对应图3(c)中函数-log10(H0,4(f))的4 个无穷间断点,即4 个恒压频率点。由图3(b)可知,301.7 kHz 不仅是恒流频率点,也是ZPA 频率点;330 kHz 不仅是恒压频率点,也是ZPA 频率点。将系统工作频率从301.7 kHz切换到330 kHz,便可在保持ZPA 的前提下,将系统从恒流输出模式切换到恒压输出模式。
从逆变器的角度看来,虽然系统一直处于谐振状态,但是在恒流和恒压模式中,系统内部的谐振关系是不同的。通过式(13)、式(14)可知,恒流模式为前3 个回路组成的整体和后3 个回路组成的整体谐振;而由式(18)、式(19)可知,恒压模式为4 个回路组成的整体和第2、3 个回路组成的整体谐振。
上述分析均是建立在忽略ESR 的前提下,如果需要考虑ESR,那么恒流增益和恒压增益可能会在负载大范围变化时出现一定程度的波动。为了简化分析,假定ESR 相同,都为r。根据式(25)和式(26)可绘制图4,其展示了在不同的ESR 下,恒流模式中的电流增益Gcc、恒压模式中的电压增益Gcv、输入阻抗角随负载变化的曲线。
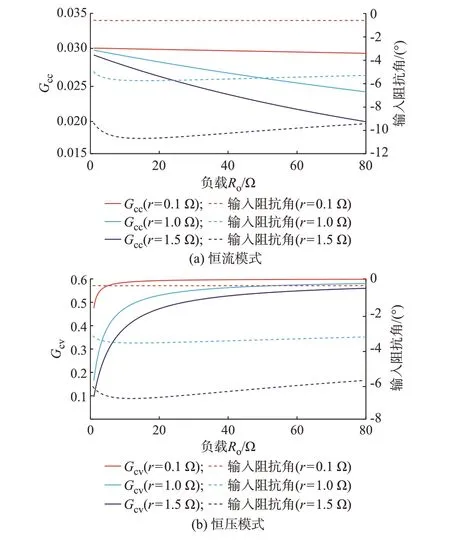
图4 四线圈多中继WPT 系统输出增益、输入阻抗角随负载变化的曲线Fig.4 Curve of output gain and input impedance angle of four-coil multi-relay WPT system varying with load
由图4 可知,当考虑ESR 时,Gcc、Gcv、输入阻抗角都会一定程度偏离额定值0.03 和0.6,且ESR 越大,Gcc、Gcv、输入阻抗角的偏离 程度越大。Gcc会随着负载的增大而减小,Gcv会随着负载的增大而增大,逼近其额定恒压增益。此外,在存在ESR 时,输入阻抗角可能呈容性,将使得逆变器无法工作在零电压开关状态,降低系统效率。为了稳定Gcc和Gcv,并避免系统呈容性,可对补偿参数或者系统工作频率进行微调。
采用控制变量法,可绘制各个补偿电容微小变化对Gcc、Gcv、输入阻抗角的影响曲线图[25],见附录B图B2。由图B2 可知,在恒流和恒压模式中,系统输出对电容变化的敏感程度不同,且稍微减小电容C3的值,可以增大输入阻抗角和Gcc,同时对Gcv的影响也较小。
整个四线圈多中继WPT 系统的效率η分别由逆变器的效率ηdc-ac、交流部分的效率ηac-ac、整流器的效率ηac-dc组成,且η=ηdc-acηac-acηac-dc。这三部分的效率如下:
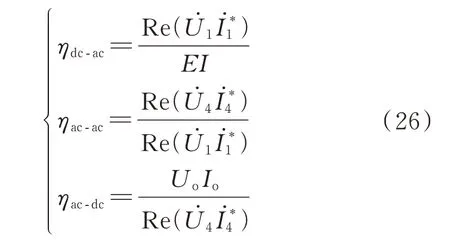
式中:上标“*”表示取共轭;I为逆变器输入电流的有效值。
根据式(4)、式(5),且在式(12)成立的基础上,交流部分的效率可进一步推导为:
利用式(27),可在已知线圈参数、ESR 值、交流负载的情况下,确定多中继WPT 系统的交流效率。
3 实验验证
基于附录B 表B1 所示参数,搭建了一个直流输入电压为40 V、充电电压为24 V、充电电流为1.2 A的四线圈多中继WPT 系统原理样机,样机照片见附录D 图D1。实验的实测数据见图D2—图D4。
从附录D 图D2 展示的恒流、恒压模式下的逆变器输出波形和负载波形可知,恒压增益和恒流增益与预期一致,电压波形与电流波形几乎同相,故也实现了ZPA。从图D3 恒流模式切换到恒压模式的暂态波形可知,由于系统并非绝对理想,故切换前后负载电压和电流均有微弱的变化。进一步对图D4(b)中的负载电压、负载电流和图D4(c)中的负载电压、负载电流进行对比,可以发现在频率切换后的瞬间,负载电压降低了0.65 V,负载电流降低了0.032 A,分别只占额定输出电压和电流的2.7%和2.6%,均在可接受的范围之内,即在切换瞬间,保持了较好的恒流和恒压特性。
图5 为充电过程中系统的输出电压、电流和效率随电池的等效负载变化的曲线图。恒流模式中,负载从10 Ω 变化到20 Ω 时,最大效率为83.9%,对应的负载电流从1.21 A 变化到1.2 A,变化率仅为0.8%,即在恒流充电阶段,保持了较好的恒流输出特性。当检测到负载电压上升到24 V 时,数字信号处理器(digital signal processor,DSP)将系统的工作频率从301.7 kHz 切换到330 kHz。在恒压模式中,负载从20 Ω 变化到80 Ω,最大效率为83.7%,对应的负载电压从23.5 V 变化到24.6 V,变化率仅为4.67%,即在恒压输出阶段,保持了较好的恒压输出特性。根据前面的论述,切换瞬间的电流和电压变化幅度也比较小,所以可以认为,在整个充电过程中,系统基本实现了先恒流输出再恒压输出。
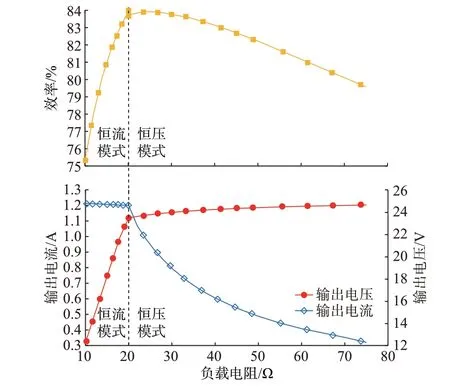
图5 输出电压、输出电流、效率随负载变化的曲线Fig.5 Curves of output voltage, output current and efficiency varying with load
4 结语
本文基于多中继WPT 系统,研究了恒流频率、恒压频率、ZPA 频率、恒流增益和恒压增益与系统系数矩阵之间的定量关系。通过切换逆变器的开关频率,使系统从恒流且ZPA 输出的频率点跳转到恒压且ZPA 输出的频率点,以实现恒流/恒压输出。实验搭建的四线圈多中继WPT 系统表明,当工作频率为301.7 kHz 时,该四线圈多中继WPT 系统体现出较好的恒流特性;当工作频率为330 kHz 时,体现出较好的恒压特性,且在整个过程中,输入阻抗角始终几乎为零。这种基于多中继WPT 系统,通过变频切换实现恒流/恒压输出的方法,为多中继WPT 系统应用于OME 充电领域的研究提供了一定的借鉴。
本文提出的方法虽然避免了额外的元件和复杂的控制,但是需要采集负载的电压和电流并以无线通信方式反馈到能量的发送端以切换逆变器的工作频率。通信和多级参数的可靠性问题可能造成系统抗干扰能力弱,导致本文方案在当前实际工程应用中面临一定困难。下一步的研究将着眼于解决此类问题,探究避免远距离通信、降低系统参数敏感性的方法。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

