考虑运行环境影响的海上双馈风电机组状态判别
魏书荣,闫梦飞,任子旭,符 杨,王 毅,王栋悦,潘 捷
(1. 上海电力大学电气工程学院,上海市 200090;2. 上海绿色环保能源有限公司,上海市 200433;3. 国网上海市电力公司电缆分公司,上海市 200072)
0 引言
目前,海上风电是中国东南沿海电网重要的本地电源,也是实现中国“碳达峰·碳中和”目标的关键技术路径之一。海上风电近年来发展迅猛,呈现出深远海化、大规模化趋势[1]。与陆上风电相比,海上风电年利用小时数多、平均风速高、单机容量大,但海上环境恶劣,风电机组故障率高[2]、维护困难[3]、停运损失大。因此,迫切需要及时精准地识别风电机组早期故障,防止故障迅速恶化带来巨大损失。
现有的海上风电机组状态判别方法大都沿用陆上风电机组的判别方法,主要基于数据采集与监控(SCADA)系统,采用经典方法[4-5]、数据方法[6-7]和智能学习[8-9]等技术。目前,已有相当数量的研究通过风电机组风速和功率的数据分析,实现风电机组的状态判别。文献[10]提出了一种自动功率曲线的监测方法,该方法已成功应用于韩国YeongHeung风电场。文献[11]构建了风速和功率的Copula 函数曲线图,进一步分析了叶片故障和偏航故障时对应的不同曲线特性。文献[12-13]均从功率预测残差的角度进行风电机组状态监测。
但上述研究都未考虑运行环境因素的影响。实际工程运行经验表明,海洋诸多环境因素对海上风电机组故障影响巨大,不可忽略。文献[14-15]指出,海上风电机组故障率相比陆上提高了61%,海上风速骤变是其中的主要问题之一。文献[14]证实了齿轮箱、发电机和轮毂这些部件更易在多变的风速条件下故障,同时,较高的风速制约着风电机组维护的可及性[16]。温度和湿度也是重要的影响因素,文献[17]对德国Fehmarn、Krummhörn 和Ormont 这3 个地点的风电机组故障率及其天气数据进行了相关性分析。统计发现,海上运行环境参数与风电机组故障的互相关率最高达到31%,其中,温度会产生季节性影响,秋季或早春的互相关率最高,湿度对电气部件的影响比机械部件更严重。但是,相关研究采用的是年平均和月平均天气参数,数据精度不高,且仅针对额定功率为300 kW 的小容量风电机组进行分析。以上针对各种环境因素对风电机组故障率的影响研究均为单独建模,即每次只考虑单一环境参数条件,忽略了因素之间的并存性和相关性[15]。
针对上述问题,本文提出了一种风电机组状态判别方法,该方法同时考虑了风电机组状态变量和运行环境影响。首先,分析海上风电机组风速、功率、温度、湍流之间的相关性,基于上述变量间的相关度,通过非参数核密度估计得到单一变量的核密度函数和边缘分布函数。然后,将其用于构建风电机组正常和故障状态下的多元Copula 函数模型,并进行模型优选,以表征多维数据间的联合概率。最后,基于贝叶斯决策理论进行风电机组状态判别,用海上风电场的实际算例验证所提方法的可行性和有效性,分析不同运行环境因素对风电机组状态判别结果的影响。
1 风电机组状态变量与运行环境因素的相关性分析和核密度估计
1.1 状态变量与运行环境因素间的相关性分析
Kendall 秩相关系数可用于表征两个特征间的相关紧密程度。以海上风速、功率、温度、湍流为研究对象,设x1和x2为其中任意两个变量,则两变量间的Kendall 秩相关系数τ为:
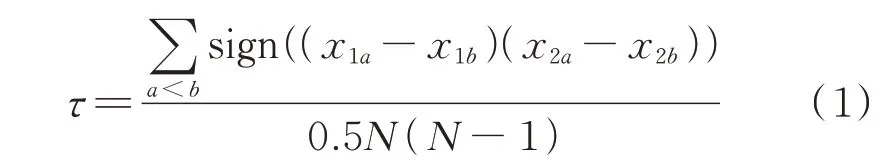
式中:x1a、x2a和x1b、x2b分别为两个变量的第a和b个观测值;N为样本容量;sign(·)为符号函数,当(x1ax1b)(x2a-x2b)>0 时sign=1;当(x1a-x1b)(x2ax2b)=0 时sign=0,当(x1a-x1b)(x2a-x2b)<0 时sign=-1。
当τ值为1 时,说明两个变量间具有正相关特征;为-1 时,具有负相关特征;为0 时,两个变量完全独立,以此定量描述变量间的相关性强弱。
1.2 单一变量的非参数核密度估计
1.2.1 核密度函数
非参数核密度估计直接利用历史数据计算每个变量的概率密度函数,无须预先假设分布,具有较好的拟合效果。假设有N个样本x1,x2,…,xN,对于一个新样本x,其概率密度函数的非参数核密度估计f̂h(x)为:

式中:xi为在第i个采样点的样本数据;h为窗宽;K(·)为核函数。
1.2.2 核密度函数的参数设定
核函数的形式有多种选择,常用的有高斯核、Epanechnikov 核、四次方核等。研究表明[18],当窗宽h一定时,不同的核函数对于概率密度函数建模的精确性影响不大。高斯核函数具有良好的光滑度和可微性,故本文选用高斯核函数作为核密度估计的核函数,对于变量m,其核函数表达式K(m)满足:

将上式代入式(2)可得:
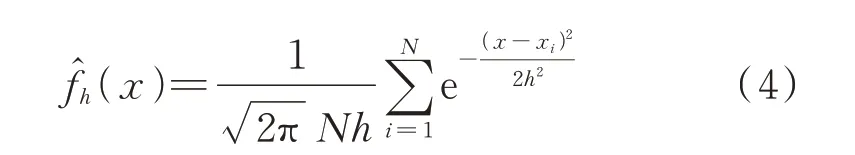
窗宽h的大小与拟合的平滑度有关,窗宽过小导致的欠平滑与窗宽过大导致的过平滑都将直接影响拟合精度,因此通常采用经验窗宽。然而,当变量的真实分布与正态分布偏离较大时,采用经验窗宽所得的核密度估计的效果并不理想,故本文采用文献[19]提出的方法求取最优窗宽,具体步骤如下。
1)选取两个分别服从N(0,1)和N(0,4)的高斯核函数K1(m)和K2(m),即
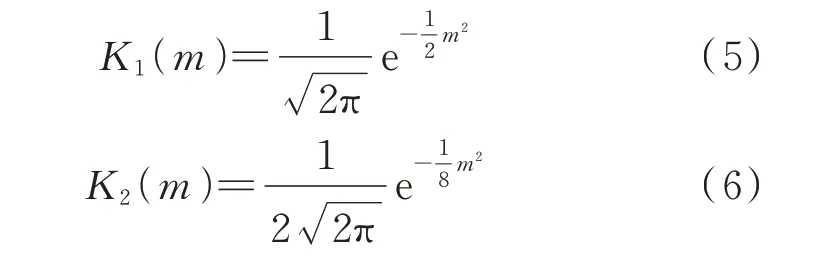
将式(5)和式(6)代入式(2)得到两个核密度函数f̂1(x)和f̂2(x)。
2)基于两个核密度函数的积分方差(integral square error,ISE)最小原则确定最优窗宽,ISE 值IISE的表达式如下:

式中:xi1和xi2表示核密度函数相应位置的样本值。
将式(8)所示模型取最小值时可得最优窗宽h,将其代回式(4)可求得此时每个变量的核密度函数。
基于上述非参数核密度估计流程可分别求得海上风速、功率、温度、湍流样本的核密度函数f(x),并对其积分求取相应的边缘分布函数F(x)。
2 联合贝叶斯决策理论和Copula 函数的风电机组状态判别方法
本文提出联合贝叶斯决策理论和Copula 函数的海上风电机组状态判别方法(用BCDM 表示)。利用Copula 函数刻画不同因素间的相关性,融入贝叶斯决策理论并代替其原始独立假设,实现风电机组状态的有效判别,是一种有监督学习的判别方法。
2.1 贝叶斯决策理论
贝叶斯决策理论是一种解决模式识别问题的统计方法。风电场SCADA 系统通常以一定的时间间隔采集风电机组各部件的状态变量和运行环境参数,此时每台风电机组的运行状态可由一个属性向量x=[x1,x2,…,xp]表 示,其 中x1,x2,…,xp代 表每台风电机组各监测变量,令
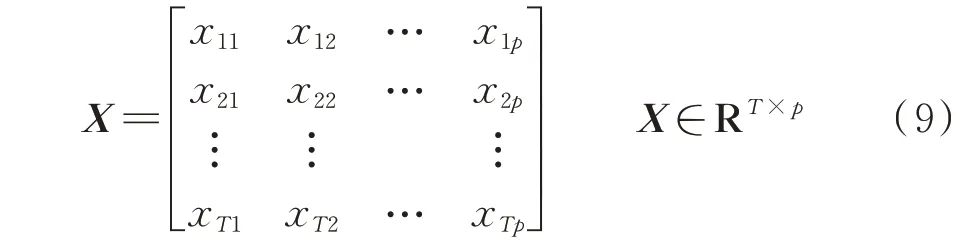
此时X共有p个监测变量,每个监测变量具有T个观测值。矩阵中的每行参数对应风电机组现场工况记录中的一种状态,相应的类标签设为Ck(k=1,2),本文仅考虑风电机组处于正常(C1)和故障(C2)两种状态。
当给定某时刻一个新的观测值x,通过贝叶斯公式可以分别计算风电机组属于正常状态和故障状态的概率,从而实现风电机组的状态判别。贝叶斯公式如下所示:

先验概率P(Ck)可通过在样本数据中计算属于某一类别的数据个数除以样本数据总数得到。计算p(x|Ck)时为了简便考虑,通常假定属性变量相互独立[20],但实际情况中,变量间可能存在一定的相关性,故本文考虑采用Copula 函数进行变量间的相关性量度代替原始独立假设。
2.2 Copula 函数
Copula 函数最早由Sklar 提出[21],可用于描述变量间的复杂相关关系。该理论表明,任何多维变量的联合分布函数都可以通过单一变量的边缘分布函数和一个Copula 连接函数组合而成。
令H为随机变量x1,x2,…,xp的联合分布函数,F1(x1),F2(x2),…,Fp(xp)为随机变量的边缘分布函数,如果所有的边缘分布函数都是连续的,那么存在一个唯一的Copula 函数C满足:
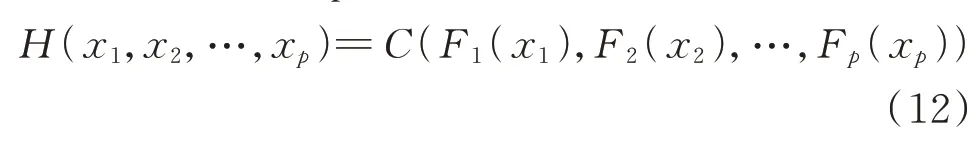
由式(12)推导可得随机变量的联合密度函数g为:

式中:c(F1(x1),F2(x2),‧‧‧,Fp(xp))为p维随机变量的Copula 密度函数;fj(xj)为每个随机变量xj的核密度函数。
结合贝叶斯决策理论和Copula 函数,联立式(11)和式(13)可得:
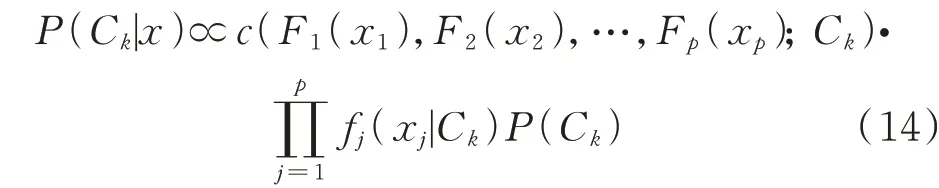
式 中:c(F1(x1),F2(x2),‧‧‧,Fp(xp);Ck)表 示 属 于类别Ck的Copula 密度函数;fj(xj|Ck)表示属于类别Ck的核密度函数。
Copula 理论解决了多元随机变量边缘分布函数已知而联合概率密度难以求解的问题,更好地刻画了风电机组状态变量和运行环境参数间的相关特性。
2.2.1 风速、功率、温度、湍流的4 维Copula 函数模型
常 用 的Copula 函 数 有Gaussian Copula、t-Copula、Gumbel Copula、Clayton Copula、Frank Copula 这5 种。不同的Copula 函数描述了数据间不同的对称特性和尾部特性,故对风速、功率、温度和湍流数据进行相关结构建模时需要选择合适的Copula 函数。目前,应用Copula 函数的研究大多基于二元变量,本文在文献[22]的基础上推导了面向多元变量的Copula 密度函数,得到了考虑运行环境影响的风速、功率、温度和湍流的4 维Copula 密度函数的表达式如下所示。
1)Gaussian Copula 函数
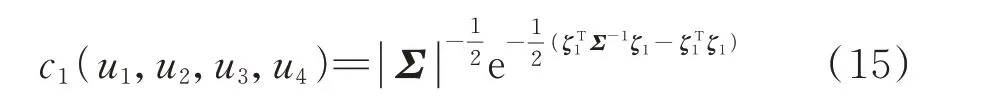
式中:u1、u2、u3、u4分别为风速、功率、温度、湍流的分布 函 数 值 ;Σ为 相 关 系 数 矩 阵 ;ζ1=[ϕ-1(u1),ϕ-1(u2),ϕ-1(u3),ϕ-1(u4)]T,其 中,ϕ-1(·)为标准正态分布的逆函数。

式 中:θ为 需 要 估 计 的 未 知 参 数;ω=(-lnu1)θ+(-lnu2)θ+(-lnu3)θ+(-lnu4)θ。
4)Clayton Copula 函数

式中:θ''为需要估计的未知参数。
2.2.2 Copula 函数的参数估计
常用的参数估计方法包括点估计法、矩估计法和区间估计法等。本文采用极大似然估计方法进行参数估计,需要估计的函数模型参数为Gaussian Copula 函数的相关系数矩阵,t-Copula 函数的相关系数矩阵和自由度以及Gumbel Copula 函数、Clayton Copula 函 数、Frank Copula 函 数 的 未 知 参数。如式(20)所示,其中参数θ*代表了各Copula 函数需要估计的参数。

式中:Fi1(xi1)、Fi2(xi2)、Fi3(xi3)、Fi4(xi4)分别表示风速、功率、温度、湍流相应的核密度函数值。
2.2.3 Copula 函数模型优选
Copula 密度函数描述了变量间的相关性特点,不同函数的选择对应了数据间不同的分布特性。为了评估Copula 密度函数的拟合优度,本文采用赤池信息准则(Akaike information criterion,AIC)和贝叶斯信息准则(Bayesian information criterion,BIC)来评价,AIC 值IAIC和BIC 值IBIC的表达式如下:
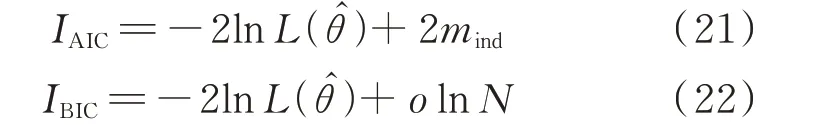
式中:θ̂表示θ的最大似然估计;o为模型参数个数;mind为独立参数的数目;L(·)为似然函数。
AIC 建立在熵的概念上,提供了权衡估计模型复杂度和拟合数据优良性的标准,但当样本数量过多时,容易出现过拟合的情况。故在此基础上引入了具有相对更大惩罚项的BIC,可有效防止模型精度过高造成的模型复杂度过高问题。综上,AIC 和BIC 值较小的Copula 密度函数因其具有较好的拟合优度将被用于构建类条件概率密度函数。
2.3 BCDM 的状态判别流程
以风电机组SCADA 系统数据中记录的风速、功率、温度、湍流4 种状态参数为研究对象,考虑了这4 种参数不同的组合情况,组合1 为风速、功率;组合2 为风速、功率、湍流;组合3 为风速、功率、温度;组合4 为风速、功率、温度、湍流,以研究不同运行环境因素对风电机组状态判别结果的影响。
联合贝叶斯决策理论和Copula 函数的风电机组状态判别过程大致分为以下几步,具体流程如图1 所示。

图1 状态判别流程图Fig.1 Flow chart of state discrimination
步骤1:对风速、功率、温度、湍流变量进行归一化处理,消除不同量纲的影响,同时减小异常数据干扰。进一步,绘制训练数据的频率直方图和数据散点图,求取成对的Kendall 秩相关系数,挖掘数据间的相关特性。
步骤2:选择具有良好光滑度和可微性的高斯核函数,计算最佳窗宽大小,通过非参数核密度估计拟合各个变量的概率密度曲线,求取训练数据的边缘分布值。
步骤3:根据各个变量的边缘分布值,采用极大似然估计法计算4 种参数组合分别在风电机组处于正常和故障状态下,5 种Copula 函数的相关参数,并利用AIC 和BIC 进行Copula 函数的优选。
步骤4:求取测试数据的密度函数值和分布函数值,代入步骤3 中优选的Copula 函数模型,联合贝叶斯决策理论进行风电机组状态判别。与现场实际工况记录进行比对,计算所提方法判别结果的准确度,并比较4 种参数组合的判别结果。
3 算例分析
3.1 风电场数据描述与分析
本文使用中国某海上风电场的数据进行案例研究,该风电场安装了34 台3 MW 双馈异步风电机组,配置有SCADA 系统进行远程监控与数据采集,如附录A 图A1 所示。选取5 号风电机组两年的运行状态数据和海洋天气参数作为研究对象。先对风速、功率、温度和湍流数据进行筛选,筛除了因通信故障、传感器故障、人为停机和弃风等原因所导致的异常数据,以减少对后续研究产生的干扰。
3.2 算例结果
3.2.1 海洋天气与风电机组故障率互相关性分析
根据德国Krummhörn 海上风电场的天气与风电机组故障率的互相关系数的求解公式[17]可得Krummhörn 海上风电场最大风速、湍流与风电机组故障率的互相关系数均为0.31,温度与故障率的互相关系数为0.28。
本文参考该互相关系数求解过程,计算中国某海上风电场5 号风电机组连续两年的月故障率,风速、温度和湍流数据的月平均值,求得该机组的月故障率与其运行环境之间的互相关系数。其中,风速与故障率的互相关系数最高,其值为0.48;温度、湍流与故障率的互相关系数分别为0.22 和0.36,与文献[17]中的结果相近,表明海洋环境与风电机组故障间的确存在一定的相关关系,在进行海上风电机组状态判别时有必要考虑天气因素的影响。
3.2.2 风速、功率、温度、湍流间相关性分析
通过对风速、功率、温度、湍流样本的分析处理,挖掘了单一变量的分布特点以及两特征变量间的依赖性和相关性,结果如附录A 图A2 所示。
附录A 图A2 中对角线位置所示为风速、功率、温度、湍流样本的频率直方图,右上部分表示的则是参数之间的相关性数据。由图A2 可知,风电机组状态参数和运行环境参数不符合常规分布,而核密度估计无须假设预先分布,故利用第1 章优化窗宽后的核密度函数直接拟合密度函数曲线,结果显示了较好的拟合效果。图A2 中右上角的数值为对应行列参数间求取的成对Kendall 秩相关系数,由数值分析可得,变量间存在一定的相关性。其中,风速和功率呈现很强的正相关,其值为0.809,接近于1;风速和湍流也呈现正相关,其值为0.595 3;而温度和其他参数间的相关性不强,其值接近于0,由此表明采用Copula 函数描述多元变量间相关关系的必要性。图A2 中左下角表示的是对应行列两两数据间的散点图,进一步反映了成对变量间的关系特性,图中多呈现宽带分布,说明变量具有较大的动态变化范围,但是从图中无法直观地确定数据间的特定关系。
3.2.3 结合运行环境影响的风电机组状态判别
为了进一步确定运行环境因素对风电机组状态判别的影响,首先,根据现场的状态记录将风速、功率、温度和湍流数据分为正常数据和故障数据两类,分别提取其中的80%用于训练正常和故障两种状态下的Copula 密度函数模型。针对4 种参数的组合,分 别 建 立 基 于Gaussian Copula、t-Copula、Gumbel Copula、Clayton Copula、Frank Copula 的5 种Copula 密度函数。然后,采用AIC 和BIC 挑选出正常和故障状态下的最优Copula 函数模型。考虑不同气象环境参数下的AIC 和BIC 值如表1 至表4 所示。
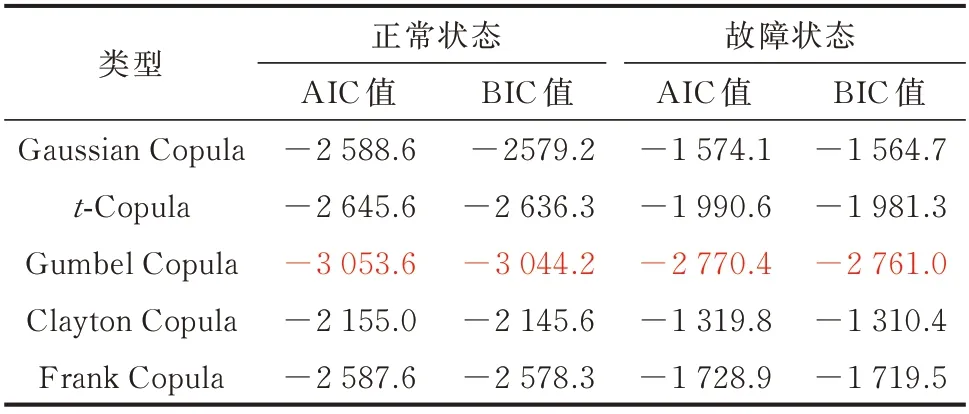
表1 风速、功率的Copula 函数模型的AIC、BIC 值Table 1 AIC and BIC values of Copula function models for wind speed and power

表2 风速、功率、温度的Copula 函数模型的AIC、BIC 值Table 2 AIC and BIC values of Copula function models for wind speed,power and temperature

表3 风速、功率、湍流的Copula 函数模型的AIC、BIC 值Table 3 AIC and BIC values of Copula function models for wind speed,power and turbulence
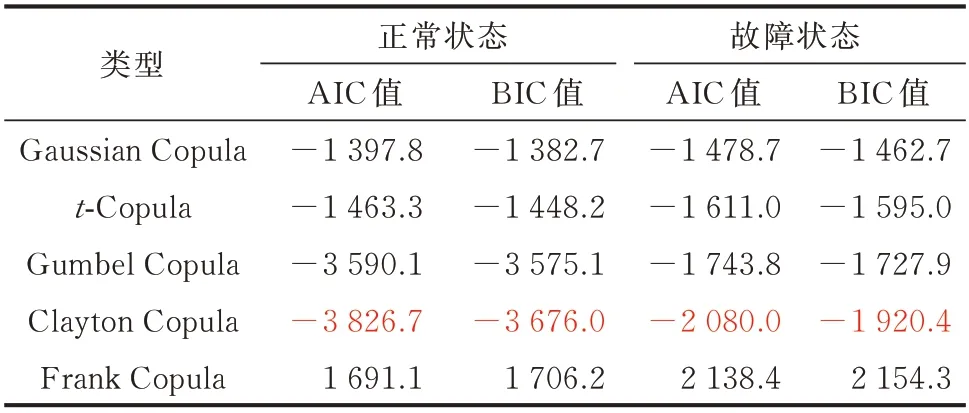
表4 风速、功率、温度、湍流的Copula 函数模型的AIC、BIC 值Table 4 AIC and BIC values of Copula function models for wind speed,power,temperature and turbulence
表1 至表4 中的红色数字表明了不同变量组合下,AIC 和BIC 最 小 值 对 应 的Copula 函 数 类 型,即所要挑选的最优Copula 密度函数。由表中数值结果可得,输入特征不同时,对应的最优Copula 函数类型不同。风速和功率采用Gumbel Copula 函数模型;风速、功率和温度以及风速、功率和湍流均采用t-Copula 函数模型;风速、功率、温度和湍流中,Clayton Copula 函数模型在正常与故障状态均有良好表现,而Frank Copula 函数模型虽然在故障时的AIC、BIC 值很高,但正常状态的表现并不突出,因此采用Clayton Copula 函数模型。工程应用中需要根据实际输入变量进行计算,优选Copula 函数类型。
分别完成4 种参数组合下的Copula 函数模型优选后,将剩下的部分数据用作测试数据,测试结果与现场实际情况比对后得到如图2 所示的精确度。文献[11]也采用Copula 理论拟合风速和功率曲线,发现了不同故障时,风速和功率的曲线表现不同。但是,从图2 的判别结果精确度可以看出,仅考虑风速和功率时,状态判别效果较差,精确度仅为46%,存在很大程度的不确定。当增加湍流参数时,精确度达到了53%,这是因为湍流和风速间的相关性为0.595 3,使得状态判别精度有了小幅提高但不明显。而当将湍流参数替换为温度参数时,判别的结果却出现了显著提高,达到了70.25%。由此,证实了运行环境因素会对风电机组状态判别产生影响,而温度是其中重要的影响参数。
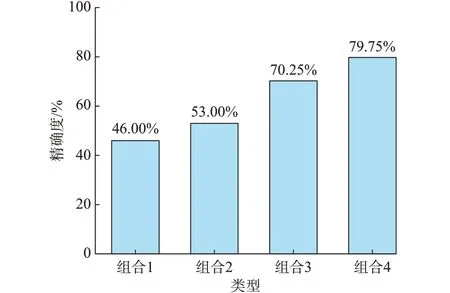
图2 4 种参数组合判别结果的精确度Fig.2 Accuracy of discrimination results of four parameter combinations
进一步,取精确度最高的组合4 的情况,即考虑了所有参数的状态判别,将该算法的结果与高斯判别分析(GDA)方法和高斯核支持向量机(GSVM)方法进行比较。其中,前者是构建多元变量联合密度函数的常用方法,后者被认为是效果最好的分类器之一,判别结果对应的混淆矩阵如表5 所示。
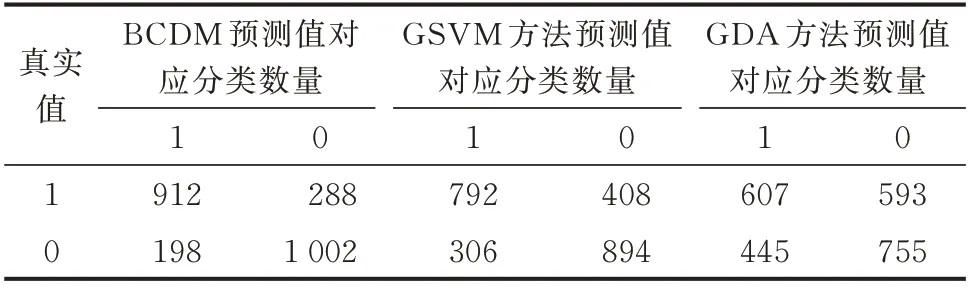
表5 不同方法的混淆矩阵Table 5 Confusion matrices of different methods
表5 中混淆矩阵的行和列代表了测试数据在不同判别方法下预测值与真实值对应的数量,其中1代表风电机组处于正常状态,0 代表故障状态,故行列对应数值相同(同为0 或同为1)时的数量代表了正确分类的数量,行列对应数值不同时的数量代表了错误分类的数量。混淆矩阵反映了在高辨识率和低误报率之间的权衡。
表5 中的BCDM 对应的是考虑4 种参数的情况,此时达到了最优的判别效果,计算可得,精确度为79.75%,而GSVM 和GDA 方法对应的精确度分别为70.25%和56.75%。GDA 方法的判别效果较差,这可能是因为原始参数的分布不接近假设的高斯分布。
进一步绘制操作特征曲线(ROC)评估各种方法的表现,如图3 所示。对应的横纵坐标分别为特异度(假阳率)和灵敏度(真阳率),特异度代表预测为正常但实际为故障的数量占所有实际为故障的数量的比例,灵敏度代表预测为正常实际也为正常的数量占所有实际为正常的数量的比例,故ROC 越靠近左上角,分类的效果越好。

图3 GSVM 方法、BCDM、GDA 方法的ROCFig.3 ROC for GSVM method,BCDM and GDA method
从图3 可以看出,BCDM 的判别效果最好。为了定量比较3 种方法的表现,采用AUC(area under curve)即曲线下的面积来进行评估,得出BCDM、GSVM 方法和GDA 方法的AUC 值分别为0.803 8、0.738 5 和0.575 5,显然BCDM 取得了最大的AUC值,验证了本文所提方法的优越性。
4 结语
运行环境对风电机组故障的影响较大,在状态判别时不可忽略。本文针对现有状态判别方法均未考虑海洋各天气因素影响的问题,提出一种联合贝叶斯决策理论和Copula 函数的风电机组状态判别方法。Copula 理论的应用精确地描述了多元变量间的相关关系,针对正常和故障时的4 种变量组合,进行了Copula 函数优选,再融合贝叶斯概率模型最终实现对风电机组的状态判别。结果表明,运行环境因素对风电机组状态判别的影响不可忽视,考虑运行环境影响的风电机组状态判别较仅考虑风速、功率的判别结果准确率提高了33.75%。此外,相比其他状态判别方法,BCDM 取得了更好的判别效果。
本文提出的方法对海上风电机组的状态判别具有明显的指导意义,并可将其延伸应用于风电机组的早期状态预测。另外,文中所选数据是基于海上风电场近两年的SCADA 系统数据得出的,但本文提出的方法同样适用于陆上风电机组,这可以作为后续研究继续深入。
本文在撰写过程中受到上海市人才发展基金项目(2020007)资助,特此感谢!
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

