提升新能源消纳能力的集中式与分布式电池储能协同规划

蔡福霖，胡泽春，曹敏健，蔡德福，陈汝斯，孙冠群

（1. 清华大学电机工程与应用电子技术系，北京市 100084；2. 国网湖北省电力有限公司电力科学研究院，湖北省武汉市 430074）

0 引言

随着中国“双碳”目标和构建新型电力系统战略目标的提出［1］，新能源发电的占比逐步提升，给电力系统的安全稳定运行带来了巨大挑战。电池储能系统具有快速的调节性能，可平抑新能源发电出力波动、消除电网阻塞，是未来电力系统中提升新能源发电接入和消纳能力的重要资源。近年来，电池储能在技术性能和环境友好性等方面都取得了显著进步［2］，单位投资成本大幅降低［3］。规模化电池储能系统已经在电力系统各个环节得到了应用，电池储能选址定容优化问题成为当前的一个研究热点［4-11］。

考虑输电网不同线路功率传输限制，文献［4］提出考虑风电、负荷预测误差相关性的集中式储能配置方法。文献［5］提出一种考虑网损的单阶段输电网和集中式储能系统联合规划模型与求解方法。文献［6］基于时序生产模拟和概率统计分析方法，研究了考虑新能源发电不确定性和弃电率约束的集中式大规模储能容量优化配置方法。文献［8］提出一种面向主动配电网的多目标分布式储能优化配置模型，以提升配电网新能源消纳和优化配电网运行。文献［9］针对配电网中分布式新能源消纳问题，提出一种分布式储能多阶段优化规划模型，并采用改进的Benders 分解算法实现对所构建问题的加速求解。文献［10］在含分布式电源配电网的储能选址定容模型的基础上，提出了考虑储能寿命修正的储能配置优化方法。

目前，针对储能配置问题的研究一般只考虑集中式或者分布式储能［12-13］。然而，在实际大型电力系统中，输电网和配电网均可能有大量新能源发电接入［14-15］，新能源的消纳需要在全网统筹。因此，从输配电网全局视角研究集中式和分布式储能的协同优化配置，能够充分发挥储能系统的作用，提升整个电力系统接入和消纳新能源发电的能力。

然而，同时考虑集中式储能和分布式储能的协同规划问题规模庞大，难以直接求解［16］。国内外针对输配电网协同规划和运行问题的研究多采用分布式优化方法［17-18］。文献［17］通过交换输配电网相连边界节点的有功功率信息，迭代更新输配电网的调度方案，实现全网协同调度。文献［18］基于分解优化建模思想，分别构建了输电网规划和配电网规划子问题，通过对双层模型迭代求解确定输配电网的规划方案。

目前，针对输配电网协同优化规划问题的研究中，输电网模型大多采用仅考虑有功功率的直流潮流模型，忽略了无功分量。因此，现有研究仅能考虑输配电网间的有功功率耦合而无法考虑无功功率交互。此外，由于输电网一般为环网结构，若直接通过松弛输电网电压约束求解输电网最优潮流模型，则无法保证解的精确性。此外，当前情况下大量电池储能以接入配电网为主，但配电网层所配置的储能同样影响着全网的能量调度。因此，考虑在全网范围内研究储能配置以促进新能源消纳。最后，考虑输配电网协同的储能配置问题包含大量整数变量，进一步增加了模型求解的复杂度。

本文针对集中式和分布式电池储能协同规划问题，考虑集中式储能接入输电网、分布式储能接入配电网，构建了考虑新能源出力和负荷不确定性的电池储能系统分层优化规划模型。该模型以不同层级电网运行成本和储能投资成本之和最小为目标，由一个输电网层储能优化配置问题和多个配电网层储能优化配置问题组成。其中，配电网层的分布式储能配置模型为混合整数二阶锥规划（mixed-integer second-order cone programming，MISOCP）问题，输电网层的集中式储能配置模型为混合整数非线性规划（mixed-integer nonlinear programming，MINLP）问题，通过变量替换和近似处理转化为MISOCP 问题。所构建的输配电网储能协同规划模型采用改进的分析目标级联法求解。

1 集中式与分布式储能协同规划基本思路

本文考虑集中式电池储能系统接入输电网，分布式电池储能接入配电网。输电网的拓扑呈网状，而配电网拓扑呈辐射状［19］。考虑到集中式与分布式储能协同优化规划问题规模大、模型复杂度高的特点，将问题分解为一个集中式储能配置问题和多个分布式储能配置问题。输电网和配电网间的有功和无功功率交换关系如图1 所示。

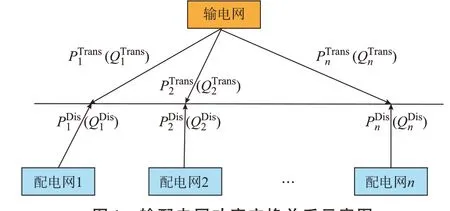
图1 输配电网功率交换关系示意图Fig.1 Schematic diagram of power exchange relationship between transmission network and distribution network

在图1 所示的输配电网耦合节点处，输电网侧交换功率变量为PTransn、QTransn，对应配电网侧交换功率变量为PDisn、QDisn。本文对集中式和分布式储能规划问题分层求解，当获得储能协同规划问题的解时，满足以下条件:

2 考虑有功和无功功率耦合的储能协同优化规划模型

2.1 分布式储能优化规划模型

2.1.1 分布式模型目标函数

2.2 集中式储能优化规划模型

2.2.1 集中式模型目标函数

集中式储能优化配置的目标是最小化储能投资、输电网运行成本和交换功率偏差惩罚项总和FTrans，即

5）线路潮流传输功率约束:

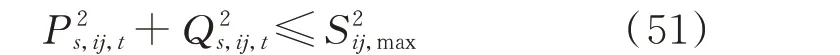
式中:Sij，max为线路ij的传输功率最大值。

6）其他电网运行约束:

3 考虑集中式与分布式储能协同优化规划求解算法

集中式与分布式储能协同优化规划是一个双层协同优化问题。其中，输电网层的集中式储能优化规划为主问题，配电网层的分布式储能优化规划为子问题。第2 章所建立的分布式和集中式储能优化规划模型分别为MISOCP 和MINLP 问题，两层问题通过耦合节点的功率交换变量关联。配电网分布式储能配置子问题可以采用成熟的算法求解。输电网集中式储能配置主问题是一个混合整数、多时段、非线性问题，难以直接求解，需要对输电网线路潮流方程进行变量替换和近似处理。

3.1 输电网潮流约束线性化

本文采用了一种考虑无功功率和电压的输电网线性潮流模型［21］，将集中式储能优化规划模型中的输电网线路潮流约束线性化。

对式（47）和式（48）中的相关变量，进行如式（55）至式（57）所示的近似处理。

式中:θij为线路ij的电压相角差；vi和vj分别为节点i和j的电压幅值。

通过对线路网损的线性化近似处理，最终得到的线路有功和无功功率方程如式（58）和式（59）所示。

式中:下标包含0 的变量θ和V分别表示某一历史运行场景中的电压相角和幅值。通过变量替换，将θ和V2视为独立变量，则式（58）和式（59）为线性约束。

因此，利用式（58）和式（59）替换输电网线路潮流约束的式（47）和式（48）后，集中式储能优化规划模型中式（15）、式（24）、式（25）和式（51）为二次约束，剩余约束全部为线性约束。至此，将MINLP 形式的集中式储能优化规划模型转化为MISOCP形式。

3.2 改进的分析目标级联法

分析目标级联法能对多层级、多主体优化问题进行协调求解［22-24］。该算法在保持各层级自身求解最优的同时，通过在不同层级间的循环迭代获得满足各层级一致性条件的最优解。对应于本文的优化问题，上层为输电网层面的集中式储能规划问题，下层为配电网层面的分布式储能规划问题，上下层间的耦合决策变量为输配电网耦合节点交换有功和无功功率。基于所建模型和迭代算法的特性，本文提出了一种改进的分析目标级联法进行求解。

考虑储能协同规划模型复杂度高、整数变量多、算例规模大等因素，本文首先将模型中的二进制变量松弛为区间［0，1］上的连续变量，在迭代前期加快模型求解收敛速度；当满足交换功率误差收敛条件后，考虑二进制变量约束并再次求解。改进的分析目标级联法的求解流程如附录A 所示。

关键步骤如下:

式中:γ为二次罚系数迭代系数。

步骤6:判断是否已添加储能投建和充放电互斥变量二进制约束。如果已添加则结束循环，否则增加二进制变量约束并返回步骤2。

4 算例分析

4.1 算例设置

算例系统由IEEE 24 节点输电网和2 个IEEE 33 节点配电网构成。其中，2 个配电网分别接入输电网节点13 和19。算例系统单线图如附录B 所示，将新能源接入节点作为配置储能的待选节点；输、配电网中的发电机、负荷和线路相关参数见文献［25-26］。

为考虑新能源出力和负荷的不确定性，应用K均值聚类方法按季节对新能源场站出力和负荷历史数据聚类生成随机场景，并将所获得的新能源场站典型出力和负荷组成系统典型日运行场景集。不同季节的新能源出力和负荷聚类场景如附录C 图C1所示。

输配电网中的新能源装机数据见表1，储能投资参数和运行参数见表2。此外，交换功率偏差 的 一 次 罚 系 数 初 始 值vs，n，t=0，二 次 罚 系 数 初 始值ws，n，t=1，二次罚系数迭代系数γ=2，收敛判据精 度ε1=0.001、ε2=0.001，新 能 源 弃 用 惩 罚 系数β=3。

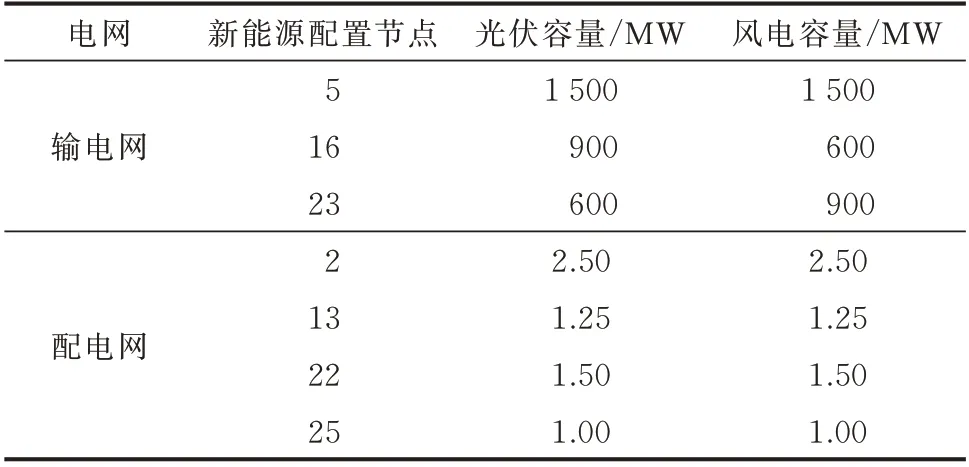
表1 输配电网中的新能源数据Table 1 Data of renewable energy in transmission network and distribution network

表2 储能投资及运行参数Table 2 Investing and operation parameters of energy storage

4.2 计算结果及分析

4.2.1 协同规划结果分析

按照4.1 节设置的参数对算例系统进行仿真验证，计算得到在输配电网中共计配置集中式储能40.79 MW/119.58 MW·h 和 分 布 式 电 池 储 能0.97 MW/4.19 MW·h，协同规划年总成本84.8 亿元。受线路损耗影响，分布式储能优先配置在距离输电网最近的配电网节点2 上。

对最优配置结果在夏季场景下的运行情况进行分析。安装在输电网节点5 的集中式储能和配电网节点2 的分布式储能的充放电功率如图2 所示。配电网1 和输电网的电源和负荷功率曲线如图3 所示。两级电网中，储能均通过在新能源高发时充电、低发时放电促进新能源的消纳。具体来说，在时段10～16 新能源高发，输电网向配电网传输功率，配电网协助输电网消纳新能源；在其余的部分时段中储能放电，输电网向配电网的传输功率因此而减小。在新能源高发时段，输电网中发电机出力降至下限820 MW，以提升新能源消纳空间。但由于新能源高发时段尖峰出力过高，储能满功率充电仍无法完全避免输配电网弃电情况产生。

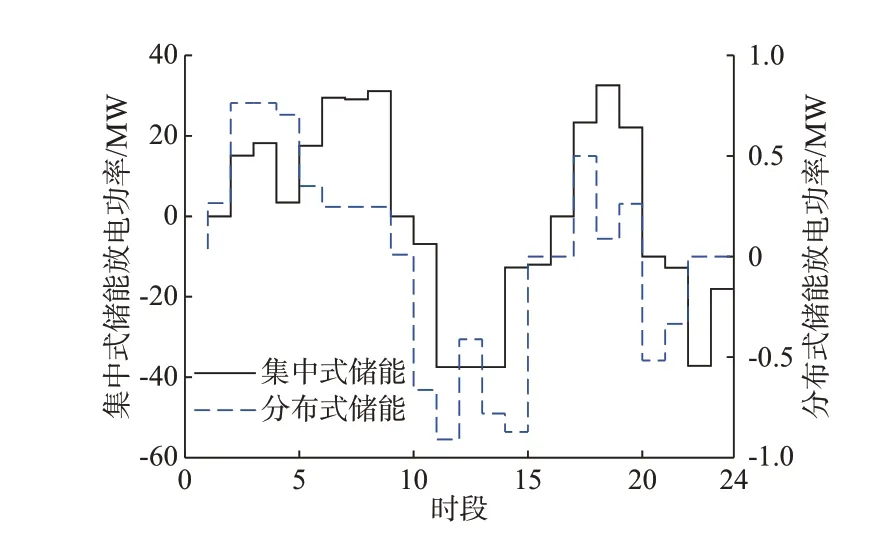
图2 夏季场景下集中式和分布式储能充放电功率Fig.2 Charging and discharging power of centralized and distributed energy storage systems in summer scenario

图3 夏季场景下输配电网电源和负荷功率曲线Fig.3 Generation and load demand power curves of transmission network and distribution network for scenarios in summer

4.2.2 协同规划效果分析

1）算法收敛情况分析

最优性误差和一致性误差的收敛过程如图4 所示。由图可知，所提算法经过7 次迭代后收敛，输配电网间的交换功率趋于一致。具体来说，一方面，集中式储能和分布式储能的优化规划模型在迭代过程中各自趋于最优，最优性误差逐渐收敛；另一方面，随着迭代次数增加，交换功率惩罚增大，输电网和配电网之间功率耦合约束逐步收紧，一致性误差逐渐收敛。

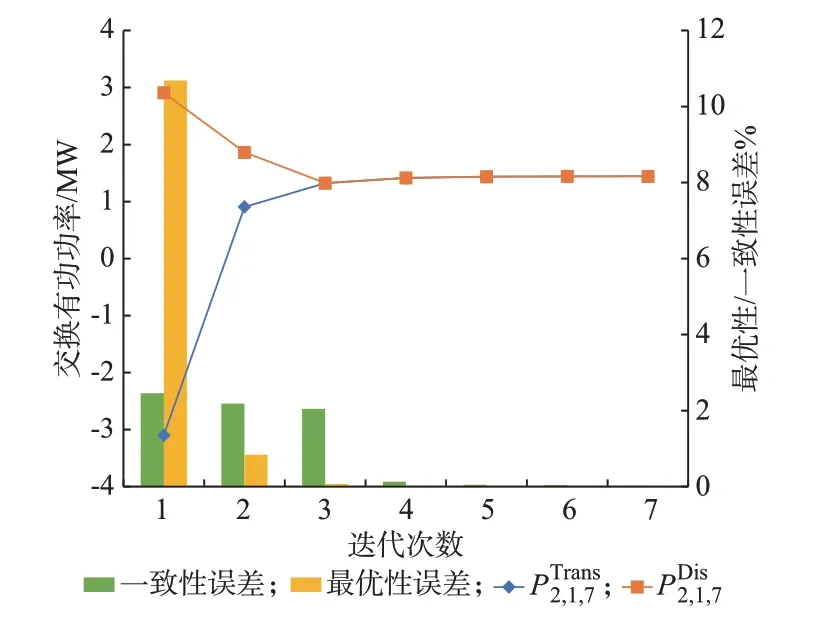
图4 所提算法收敛过程Fig.4 Convergency process of proposed solution method

2）协同规划与独立规划对比

单独针对集中式或分布式电池储能配置，以及采用本文所提出的集中式与分布式协同储能规划模型计算所得储能配置结果如表3 所示，其中储能容量成本为1 200 元/（kW·h），功率成本为300 元/kW。与协同规划相比，采用独立规划配置方法计算所得配电网分布式储能和输电网集中式储能配置规模均低于协同规划计算结果，但是，总成本比协同规划配置结果高4 752.66 万元。独立规划未考虑输配电网之间功率的交换，未能考虑全网资源互补特性，进而导致输配电网弃风弃光总惩罚相比协同规划增加了5 032.1 万元，总成本偏大。

表3 输配电网储能协同规划和独立规划计算结果Table 3 Calculation results of coordinated planning and independent planning for energy storage in transmission network and distribution network

当集中式储能无法满足输电网的新能源消纳时，配电网中的分布式储能通过充放电优化可辅助整个输配电网的新能源消纳。由于输电网功率量级较大、配电网线路容量有限且存在线路损耗等原因，远离输电网的配电网节点13 未配置储能。

综上所述，按照协同规划给出的储能配置方案可以提升电网整体运行经济性和新能源消纳能力。对实际系统，若考虑对更多的配电网进行储能协同规划，则能进一步提升协同规划效益。

4.2.3 灵敏度分析

1）储能成本

由于目前储能价格较高，利用储能提升新能源消纳所带来的收益尚未明显高于储能配置成本和寿命折损成本，储能配置能量和功率较小。

分别对储能的能量成本和功率成本进行灵敏度分析。不同储能成本下，考虑储能协同配置结果详见附录D 表D1。储能随着其价格的降低开始被配置，且配置容量和功率逐渐增加。

不同成本的储能配置后对系统各成本的影响如表4 所示。随着储能价格下降，储能配置容量增加，输配电网弃风弃光成本和发电成本下降。这也进一步说明，配置储能可以有效促进新能源消纳，减少传统火电机组的发电量，提升输配电网整体运行的经济性。

表4 在不同设备成本下输配电网储能协同规划的综合成本Table 5 Overall cost of coordinated planning for energy storage in transmission network and distribution network with different equipment costs

2）化石能源碳排放成本

考虑电力系统的低碳化转型趋势和碳排放市场的发展［27］，从使用新能源所带来环保效益的角度出发，增加化石能源的碳排放成本以提升新能源消纳动力。对于煤电机组，碳排放强度为0.8 t/（MW·h）［28］，以碳排放价格100 元/t 为例，可以等效认为每利用1 MW·h 新能源可减小0.8 t 碳排放，从碳排放市场上获得80 元的收益。

据此，结合论文设定的储能成本参数，计算得到不同碳排放价格下的储能配置结果、新能源减排收益和系统总成本详见附录E。随着碳排放价格的提高，配置储能的功率和容量、新能源的消纳量和减排收益随之增加，系统总成本随之降低。增加利用新能源的碳排放收益项之后，通过在输配电网中合理配置储能，可以有效提升新能源消纳以获取环保收益，大幅降低输配电网的总投资运行成本。

5 结语

本文以提升电网新能源消纳为出发点，以降低输配电网运行和储能投资的总成本为目标，建立了同时考虑配置集中式与分布式电池储能的协同优化规划模型。在输配电网全局层面寻求集中式和分布式储能的规划方案，将整个问题分解为输电网层的集中式储能优化配置主问题和各个配电网中的分布式储能优化配置子问题，两层问题通过输配电网耦合节点间交换的有功和无功功率联系。通过对输电网潮流约束进行变量替换和近似处理，以及对配电网潮流约束进行二阶锥松弛，将两层问题均转化为MISOCP 问题，并提出了一种考虑松弛整数约束的改进分析目标级联法求解。通过对算例系统进行仿真验证，得到如下结论:

1）相比仅针对集中式或分布式储能的配置方法而言，所提出的集中式与分布式电池储能协同优化规划方法从全网视角优化储能配置，可提升储能的利用效率，降低全系统投资和运行成本。

2）通过采用计及无功功率的线性化输电网潮流模型，可以有效计及无功功率对输电网安全经济运行的影响；针对主配电网储能优化配置的两层模型，所提出的考虑整数约束松弛的目标级联法可以加快求解速度。

3）当前电池储能成本较高，储能配置容量较小；考虑增加化石能源的碳排放成本后，将会配置更多的储能以提升新能源消纳，减小系统的碳排放量。

进一步的研究将同时考虑集中式与分布式储能协同配置和电网的扩展规划问题。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。