基于开关谐振支路的电压自平衡型ISOP 直流变压器
刘海洋,崔淑梅,刘 闯,姚 航,潘育宗
(1. 哈尔滨工业大学电气工程及自动化学院,黑龙江省哈尔滨市 150001;2. 东北电力大学电气工程学院,吉林省吉林市 132012;3. 国网吉林省电力有限公司吉林供电公司,吉林省吉林市 132000)
0 引言
随着工业应用中电力电子变换装置的电压和电流应力不断增加,模块化成为研究热点。输入串联输出并联(input-series output-parallel,ISOP)模块化电力电子变压器(power electronic transformer,PET)具有较高功率密度和灵活性,因而被广泛应用于轨道牵引[1]、新能源[2]和储能并网[3-4]等领域。
高频隔离DC/DC 级是ISOP 型PET 的关键组成部分。然而,由于成本和技术的原因,制造商很难消除电容器和磁性元件的公差,各模块的输入电压在开环运行时是不平衡的。而这种不平衡带来的电压偏置和电流偏差很可能会损坏开关和电容器。因此,输入侧均压(input voltage sharing,IVS)控制成为ISOP 变换器的基本设计要求。对于由直流变换器和级联H 桥(cascade H-bridge,CHB)组成的传统ISOP 型PET,最简单的思路是在CHB 控制器中加入直流电压反馈环路,以确保CHB 输出直流电压平衡[5]。然而,由于各个模块的脉宽调制策略不同,这些控制策略会产生大量谐波,严重污染输入侧电网[6]。此外,CHB 的平衡控制方法在空载或轻载条件下会导致计算资源不足和不可控[7]。
因此,PET 的IVS 控制设计倾向于由DC/DC级独立实现[8-9],同时也广泛应用于中压直流变压器(direct current transformer,DCT)[10-11]。一种典型方式是:由输出电压反馈回路产生一个共同的输出电压补偿,各模块的输入电压反馈回路产生各自的均压补偿,最后将2 个控制变量求和,最终得到各模块的控制器输出[12]。文献[13]提出了一种基于虚拟阻抗的直流固态变压器控制策略,该控制策略使得直流固态变压器可以在子模块功率电路参数不同的情况下,同时保证各子模块输入均压与输出均流。文献[14]采用了恒变比控制,不论是给定高压侧电压还是低压侧电压,仅采用恒变比控制环控制两侧电压变比恒定。该方式相对简单,并且当电压切换时动态响应比较快[15]。
这些IVS 控制都面临2 个问题:1)每个模块至少需要一个传感器测量输入电压信息。因此,形成了一个多输入多输出控制系统,增加了控制系统的复杂度。2)为了设计IVS 控制参数,必须对系统模型进行解耦运算,然而该解耦函数一般是在电路参数完全一致的假设下完成的。因此,降低了建模的准确性,对控制系统的鲁棒性产生了挑战[16]。
近年来,采用开关电容变换器平衡直流电容电压的方法在多电平变换器中得到广泛应用[17]。在每个开关周期内,开关电容变换器为各直流电容器建立了传递能量的通路,从而确保设备电压应力一致。然而,在这些开关电容变换器中,会不可避免地产生充放电电流尖峰,严重影响电容器的使用寿命。文献[18]提出了一种将谐振开关电容变换器电容电流抑制为谐振电流的方案,并实现了零电流开关。这种方案也被用于DCT 拓扑中,通过对每个隔离双向直流变换器(isolating bidirectional DC converter,IBDC)级联一个电压平衡变换器(voltage balancing converter,VBC)来 实 现IVS[19]。VBC 通过一个谐振支路在2 个相邻的输入串联直流电容器之间共享能量,并巧妙地在不需要额外控制器的情况下实现了IVS。但VBC 增加了大量的有源开关器件,提高了成本,也增加了损耗,降低了可靠性。
活动现场,专家结合临床案例为家长们详细介绍了0~3岁宝宝口腔发育的三个阶段,指出了每个阶段的口腔特点、常见问题以及喂养和护理方法。专家特别指出,给孩子选择更贴近母乳喂养的奶瓶,以及正确使用安抚奶嘴,对孩子口腔发育都是有帮助的。专家还提到,很多病例是因为家长缺乏必要的知识,采用了错误的喂养方式导致的。活动中,主办方安排了“口腔工具连连看”“口腔知识抢答赛”等游戏环节,家长们在愉快的气氛中巩固了所学知识。
本文提出了一种改进的DCT 拓扑结构,将开关谐振支路(switched resonant branch,SRB)集成到各双有源桥(dual active bridge,DAB)模块之间,在不增加开关器件的前提下,利用DAB 模块开关动作实现了输入侧电容之间的电压自平衡,且不增加开关损耗。文中首先介绍了所提出的DCT 拓扑结构,分析了其工作原理和支路电流应力。然后,给出了传统ISOP 型DCT 小信号模型的不足,并给出了本文拓扑的电压控制器设计,同时设计了一种可行的模块故障处理策略。最后,给出了仿真和实验验证,同时给出了传统拓扑结构与基于开关谐振支路的直流变压器(SRBDCT)拓扑结构的对比。
1 SRBDCT 拓扑与工作原理
1.1 拓扑的提出
式中:R为负载电阻;s为拉普拉斯算子。
针对C语言实践教学中暴露出来的问题,不能仅靠对教学内容进行调整来解决所有问题,要以实践和实用作为指导方针,对整个教学的过程和组织进行深入改革,实现教学改革培养实用型人才的根本目标。本研究中主要以团队合作和项目驱动这两种方法进行课程的设计。

图1 SRBDCT 拓扑Fig.1 Topology of SRBDCT
1.2 工作原理
所有开关都依照单移相DAB 的工作原理运行,而SRB 仅利用每个DAB 的一个输入桥臂。为简化分析,给出如下假设:各DAB 漏感存在公差,且Cik的容值足够高,从而忽略电压纹波。根据DAB 工作原理,SRB 在一个开关周期T内可以分为2 种状态。
状态Ⅰ:0~0.5T阶段,该状态为DAB 输入桥的正半周期,SRB1 与Ci1并联,SRB2 与Ci2并联,如附录A 图A1(a)所示。以SRB1 为例,电容Ci1中的能量传递给SRB1,SRB1 的谐振电流ir1的波形见图A2。由于SRB1 完全谐振,因此谐振电感电压vLr1必然有:
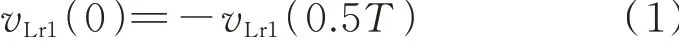
作为全球作物保护行业的领军企业之一,安道麦致力于创造简便农业,为农民提供高效的产品和服务,帮助农民简化农作生活并促进农业发展。公司拥有70多年的悠久历史,企业规模在作物保护行业里名列前茅,是一家“立足中国、联通世界”的跨国作物保护公司,2017年公司年销售额达35亿美元,中国区同比增长41.6%,实现历史最佳业绩。
基于基尔霍夫定律,且电容Ci1的电压为Vi1,则式(1)可以表达为:

DAB 电路与直流电容和SRB 并联,所以DAB运行完全不受影响。根据叠加定理,流过开关S11的电流iS11的波形见附录A 图A2。
状态Ⅱ:0.5T~T阶段,该状态为DAB 负半周期,SRB1 与Ci1和DAB2 并联。Cr1中的能量传递给Ci2,谐振电流ir1的波形见附录A 图A2。与状态Ⅰ一样,有:
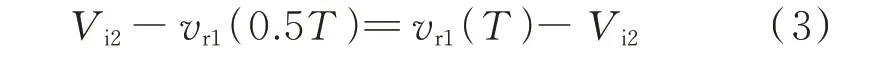
式中:Vi2为电容Ci2的电压。
联立式(2)和式(3)可得:

对于完全谐振状态下的Cr1电压有:

因此,DAB1 的输入电流i1可表示为:根据有功功率守恒定理,总传输功率Pa为:

因此,该电路保证了电容Ci1与Ci2的电压平衡总是存在。
同理,上述分析一样适用于SRB2,并保证电容Ci1与Ci3电压总是平衡。因此,2 个SRB 利用DAB输入桥总是可以实现直流电容器之间的电压自平衡。与VBC 一样,当开关状态改变时,谐振电流降至零。因此,额外的SRB 不会破坏零电压开通(zero voltage switching,ZVS)条件或增加S11的关断电流。
1.3 谐振支路应力
为了设计补偿器的传递函数Gvc1(s)和Gsc(s),就需要采用相应的解耦方法来将整个系统分解为4个独立的控制环路。因此,设计一个解耦矩阵W,令

式 中:iin为 整 个DCT 的 输 入 电 流;i1为DAB1 的 输 入电流。
综上,FCM动态监测MRD对判断AL患者的复发、预后及指导个体化治疗有较大的临床价值。但目前MRD检测时间、间隔时间及阳性阈值等尚无统一标准。此外,提高检测灵敏度也是亟待解决的问题之一。
DAB1 的传输功率为:
会计核算是企业重要组成部分,一定程度影响会计信息质量和会计信息真实性。目前企业会计核算普遍存在的问题之一即缺乏规范的会计基础工作,之所以出现这种问题多和以下方面有关:首先原始凭证填写缺乏完整;部分企业在会计核算中填写原始凭证时存在不填、少填和漏填现象,完全不符规定原始凭证填写要求,导致会计信息不准。其次原始凭证存在虚假现象;会计原始凭证填写在企业中必须符合实际发生项目内容,当前部分企业原始凭证填写存在违规编制虚假情况。第三记账凭证缺乏规范;企业会计记账凭证若不规范则对会计信息准确性产生直接影响。

式中:D为DAB 模块的移相比。
新媒体是一个多元化的平台,高校辅导员引导的是“现实的人”,在如今多种思潮与多种文化混杂的时代,高校辅导员应该用社会核心价值观的观念来主导新媒体文化,这样才能发挥“引导人”的作用。
联立式(4)和式(5)有:


式中:iSk1(k=1,2,3)为流过开关Sk1的电流;VCE为集电极-发射极饱和电压;VF为反并联二极管的正向压降;t1为DAB 电感电流的过零点对应的时刻。
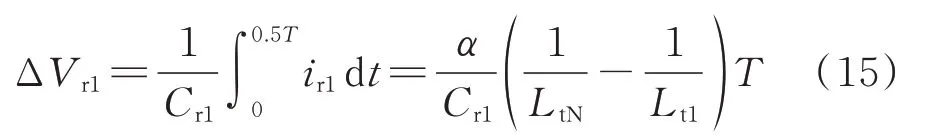
如附录A 图A4(b)所示,较高的谐振电流意味着更高的能量通过SRB 传输,因此ΔVr1也有增加。此外,当比率Lr1/Cr1上升时,ΔVr1变得更高。通过类似的计算可以推导出SRB2 模型。
目前内固定物失效仍是肩袖修复的主要并发症之一,因此可靠的初始内固定强度对于肩袖撕裂修复十分重要。Meier等[18]通过在30例尸体的肩关节上模拟全层撕裂的肩袖损伤,分别采用穿骨缝合、单排锚钉缝合、双排锚钉缝合。其结果显示锚钉固定的抗拉力强度明显强于穿骨缝合,双排锚钉明显强于单排锚钉,且当双排锚钉固定试验的拉力强度达到设定最大限度时,仍未出现内固定失效情况,这也说明双排锚钉能为肩袖修复内固定维持提供高强度抗拉力作用。
1.4 谐振支路参数设计
通常,设计时已知DCT 的额定总功率PaN、输入电 压 的 最 小 值Vi,min和 最 大 值Vi,max。Lt为DAB 模块漏感实际值,制造商会给出DAB 模块漏感参数的设计值LtN,以及参数的误差范围δ:

将式(16)代入式(14)可得谐振支路最大电流有效值为:
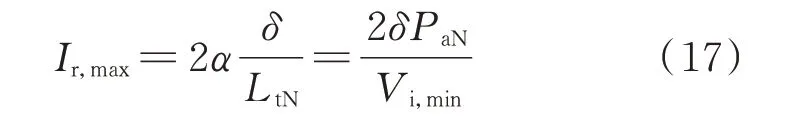
同理,将式(16)代入式(15)可得谐振电容Cr最大电压纹波为:

若VC,max为电容器的最大耐压值,则有:
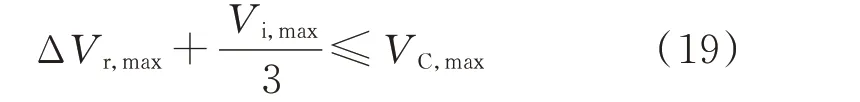
将式(18)代入式(19)可得谐振电容选取范围为:
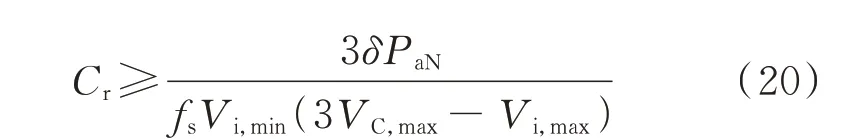
确定谐振电容容值后,可得谐振电感值为:

同时,谐振元件的最大电流有效值须大于Ir,max。
1.5 谐振支路的损耗
如前文所述,在谐振条件下,SRB 的电流总在开关状态切换时过零,因此SRB 不会产生开通和关断损耗。根据谐振电流路径,SRB 的损耗由绝缘栅双极型晶体管(IGBT)通态损耗和器件等效串联电阻损耗2 个部分组成。在半个开关周期内,SRB 桥臂的IGBT 总通态损耗为:
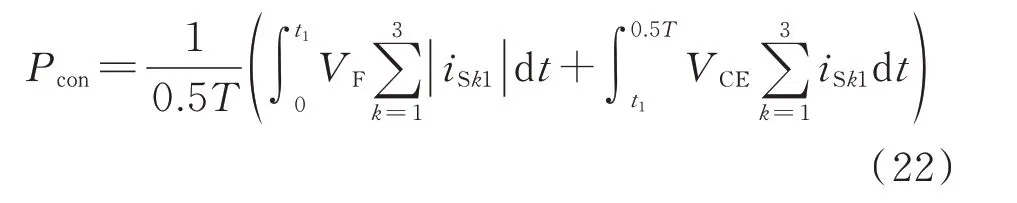
Ir1的归一化特性见附录A 图A4(a),图中曲线表明,随着输出功率的增加和Lt1公差的提高,电流Ir1变高。在没有容差的情况下,电流Ir1才会降为零,因为这2 个因素都会导致DAB 功率不平衡度增大,使得各模块输入电容器承受更多不平衡能量。对于谐振支路,Cr1上的电压纹波可以表示为:
根据叠加定理,流过开关S11、S21、S31的电流分别为:
这是怎么回事呢?原来我和好朋友任任在玩多米诺骨牌。今天我们准备搭个大工程,做个复杂的图形出来。可是计划总是美好的,现实却是残酷的。

式 中:ir2为SRB2 的 谐 振 电 流;it1、it2、it3分 别 为 流 过Lt1、Lt2、Lt3的电流。
由式(22)和式(23)可推导出IGBT 的导通损耗为:
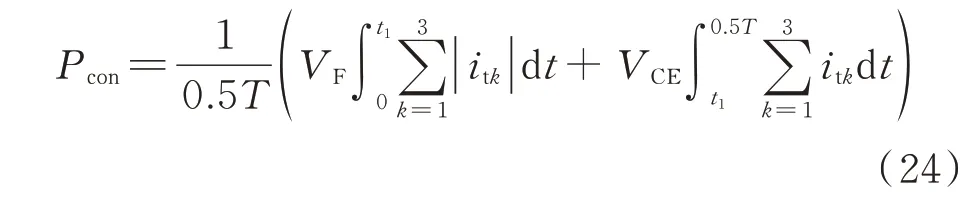
显然,式(24)中不包含谐振电流ir1和ir2,因此IGBT 的总损耗不受SRB 的影响。无源器件的损耗PESR由谐振电容、谐振电感和直流电容上的损耗构成。通过元件等效串联电阻Resr和谐振电流有效值Ir可计算得:

2 SRBDCT 控制系统
2.1 传统IVS 控制系统设计
基于3 个DAB 模块的传统ISOP 型DCT 控制系统如图2 中蓝色虚线框部分所示。

图2 传统ISOP 型DCT 和SRBDCT 控制方案Fig.2 Control schemes of traditional ISOP-type DCT and SRBDCT
传统ISOP 型DCT 控制系统包含了一个输出电压调节(output voltage regulating,OVR)环路,其中Voref为输出电压参考值,v̂o为输出电压的采样值,Gvc1(s)为OVR 环路补偿器的传递函数,d̂1、d̂2和d̂3分别为DAB1、DAB2 和DAB3 的输出电压补偿。此外,各DAB 模块拥有各自的IVS 控制环路,其中各输入电压采样值为v̂i1、v̂i2和v̂i3,Gsc(s)为IVS 补偿器 的 传 递 函 数,则 输 入 电 压 平 衡 补 偿 为x̂1、x̂2和x̂3。最后,由输出电压补偿与IVS 补偿一起产生各DAB模块的移相率。显然,在ISOP 型DCT 中,各模块控制变量对输入/输出电压的影响并不是独立的,而是经由模块间的电气连接耦合在一起,从而形成一个多输入多输出系统H:
892 Application of feature matching algorithm based on grid-based motion statistics in medical service robot
The electric field at the gate–oxide and channel interface is assumed to be continuous in GSGCDMT-SON MOSFET, we have
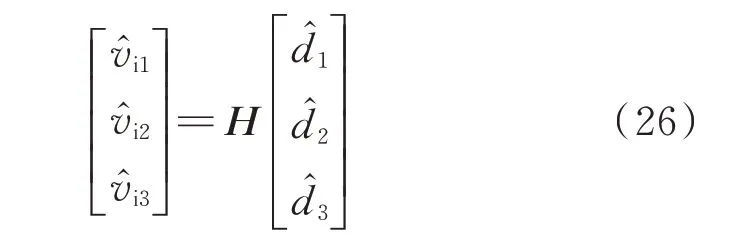
SRB 的 工 作 原 理 表 明,SRB1 和SRB2 在 状 态Ⅰ下分别从Ci1和Ci2吸收能量,如附录A 图A3(a)所示,并在状态Ⅱ下将能量释放给Ci2和Ci3,如附录A图A3(b)所示。因此,为了保证电压平衡,输入电容中的能量必须维持恒定。对于DAB1,Ci1上的电荷守恒,可以表示为:

联立式(26)和式(27)得:
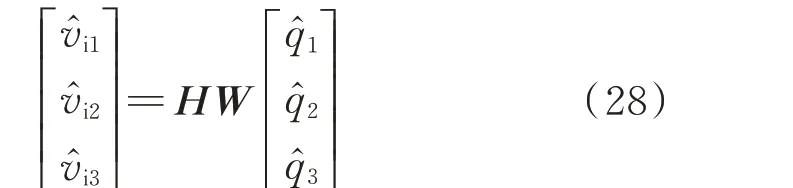
只要矩阵乘积HW为一个对角矩阵,各模块的控制变量q̂1、q̂2、q̂3与模块的状态变量v̂i1、v̂i2、v̂i3就形成了一对一的关系,如图2 中红色虚线框部分所示,从而实现控制器的设计。为了简化建模与解耦的计算量,假设所有模块的参数是一致的,则H为对称矩阵,且W为纯实数矩阵[12-13]。此时,不论是控制器设计的计算量,还是解耦环节的实现都是可行的。然而,对于一个存在公差的模块化DCT 来说,现实中的H为非对称矩阵且秩不为0,若依然采用理想模型得到的W矩阵,则无法实现完全解耦,使得设计的IVS 控制器出现稳定性风险。若采用实际参数的H矩阵,一方面,测量所有精确参数存在难度;另一方面,求出的解耦矩阵W为一非实数矩阵,使得解耦环节在控制器实践中变得复杂。
文献[20]采用前述的传统解耦算法得到了包含3 个DAB 模块的ISOP 型DCT 的小信号模型,基于该模型可得到第1 个DAB 模块的输入电压变量v̂i1与 其 均 压 控 制 变 量q̂1之 间 的 传 递 函 数 为:

图1 为本文提出的SRBDCT 拓扑。图中,3 个DAB 模块采用ISOP 配置,Vi为变压器输入侧电压,Vo为输出端电压,每个DAB 模块在输入侧都有一个直流母线电容Cik(k=1,2,3)和一个变比n=1的高频变压器。Lt1、Lt2和Lt3为各变压器的漏感。SRB 连接各相邻模块输入侧桥臂的中点。每个支路由一个电感Lrj(j=1,2)和一个电容Crj组成,每个支路的谐振频率等于DAB 开关频率fs。支路通过交换直流母线电容器中的能量以实现电压自平衡。
基于实验样机参数搭建了一个包含3 个模块的ISOP 型DCT 的Simulink 仿真模型,通过测量得到该传递函数如附录A 图A5 中红色圆点所示,图A5中蓝线为式(30)计算结果。对比可以发现,采用传统解耦技术的均压环小信号建模结果与实际模型存在一定的差距。若基于该模型进行均压环的控制器设计可能导致控制系统出现不稳定风险。模块间参数差距越大,模型精度越低,这一风险就越显著。
2.2 SRBDCT 电压控制设计
SRBDCT 控制系统如图2 中绿色虚线框部分所示,其中d̂为移相率。与传统ISOP 型DCT 控制系统相比,SRBDCT 由于具有输入侧电压自平衡的特性,因此不再需要IVS 控制环,SRBDCT 自身的自平衡特性取代了图2 中红色虚线框所示的IVS 控制环的作用。此时,SRBDCT 仅需设计OVR 环路来调节DCT 输出电压就足够了,无须采用解耦运算与前提假设。因此,相较于传统的IVS 控制系统,SRBDCT 控制器复杂度与设计难度都更低,在工程实践中具有优势。如图2 中绿色虚线框部分所示,SRBDCT 系统的OVR 控制器中,Gvd(s)为基于实验参数的SRBDCT 小信号模型,该OVR 开环增益为:
因刘勰本人深受各家思想的影响,故在《文》一书中有将儒道佛及诸子各家繁杂思想交叉的现象,要想梳理道家思想对《文》一书的影响,就必须理清《文》中是否有引用(化用)道家思想的情况,现逐一摘录如下:
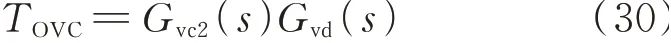
式中:Gvc2(s)为SRBDCT 系统OVR 环路补偿器的传递函数。
式中:vr1为谐振电容Cr1的电压。
若 采 用 比 例(proportional,P)补 偿 器,令Gvc2(s)=0.001 7,此 时TOVC见 附 录A 图A6 中 蓝 色虚线。虽然P 补偿器保证了控制回路的稳定性,但TOVC在低频段接近0 dB,会产生较大的稳态误差Evo(s),如下式所示:
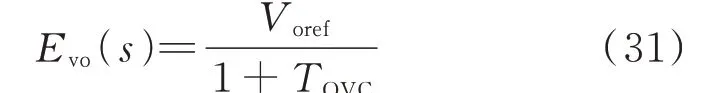
为了增加低频TOVC,采用比例- 积分(proportional-integral,PI)补偿器,则
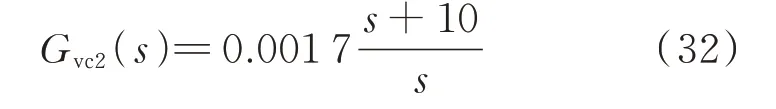
如附录A 图A6 红色实线所示,0.1 Hz 时TOVC大于20 dB,能够有效降低稳态误差,且保证系统稳定。
3 模块故障处理策略
针对本文提出的SRBDCT 拓扑结构,附录A 图A7 给出了一种基于冗余模块设计的模块故障处理策略,即对于SRBDCT 来说,设计之初为应对模块故障的风险,需至少存在一个模块的冗余度。以包含3 个模块的SRBDCT 为例,当模块2 发生故障后,该模块的所有开关闭锁,同时Jr2关断将故障模块与SRB 断开,J2闭合以维持输入侧的主电路连接。此时,故障模块退出SRBDCT 的运行,由剩余模块来平均承担故障模块切除后的输入侧电压与输出电流的应力。重要的是,此时2 条SRB 支路串联在一起,变为一条SRB 支路,Lr1、Lr2、Cr1、Cr2这4 个元件串联在一起有:
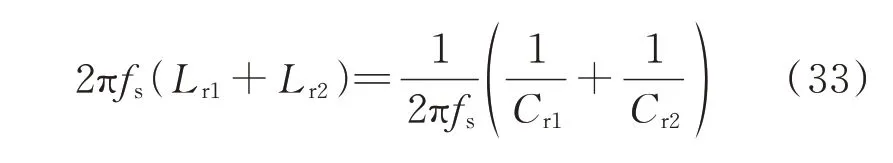
因此,新的SRB 支路依然保持原有的谐振频率fs,按照相同的原理平衡模块1 和模块3 之间的输入侧电压,流过该SRB 支路的电流依然为模块间的平衡电流。同理,若第1 个或者最后一个模块发生故障,采用同样的切除方式,此时,对应的第1 个或最后一个谐振支路会退出SRBDCT 的运行,也不会影响其余支路和模块的运行。更换故障模块后,只要断开J2,并闭合Jr2,使对应SRB 支路重新接入更新的模块,SRBDCT 就可以恢复到最初的工作状态。
4 仿真与实验验证
为了验证本文所提出的SRBDCT 的特性,根据附录A 表A1 中的参数建立了Simulink 仿真模型和1 套实验样机。实验样机额定功率为300 W,高频变压器的匝数比为1∶1。为了测试SRB,DAB 电感的不平衡比例超过15%。
4.1 谐振支路工作原理实验验证
当输入电压Vi=90 V 时,实验样机工作在降压模式,图3(a)为SRBDCT 在该模式下的负载阶跃实验波形。当负载从16 Ω 变为11.5 Ω 后,输出电压Vo依然控制在参考值30 V,而输出电流Io从1.65 A 变为2.3 A,表明该样机实现OVR 环路设计。在负载变化前后,尽管由于漏感参数不同,各DAB 模块的电流存在差异,但各模块输入电压保持均衡,即Vi的1/3,具体均压效果见表1。图3(b)所示为SRB在负载阶跃时的实验波形,可见SRB 所在的DAB桥臂开关电压(vS11、vS21、vS31)的波形在负载变化前后没有发生改变,而SRB 的电流随着负载功率的增加而上升,符合第2 章的分析。附录A 图A8 和图A9 分别为降压模式和升压模式下SRBDCT 的负载阶跃实验波形。 图A10 为功率反向传输时SRBDCT 的负载突变波形,并联侧为30 V 电压源,而串联侧的电压参考值为90 V,当串联侧负载从166 Ω 变为112 Ω 时,串联侧的均压状况依然保持。显然,在不同电压模式和负载状况及功率流向下,该SRBDCT 都能够实现串联侧的电压自平衡,具体平衡效果见表1。不同电压模式下负载变化时SRB 的开关电压与支路电流的暂态波形见图A11。可以发现,负载跳变时SRB 支路电压与电流变化平稳,且支路谐振状态保持不变。
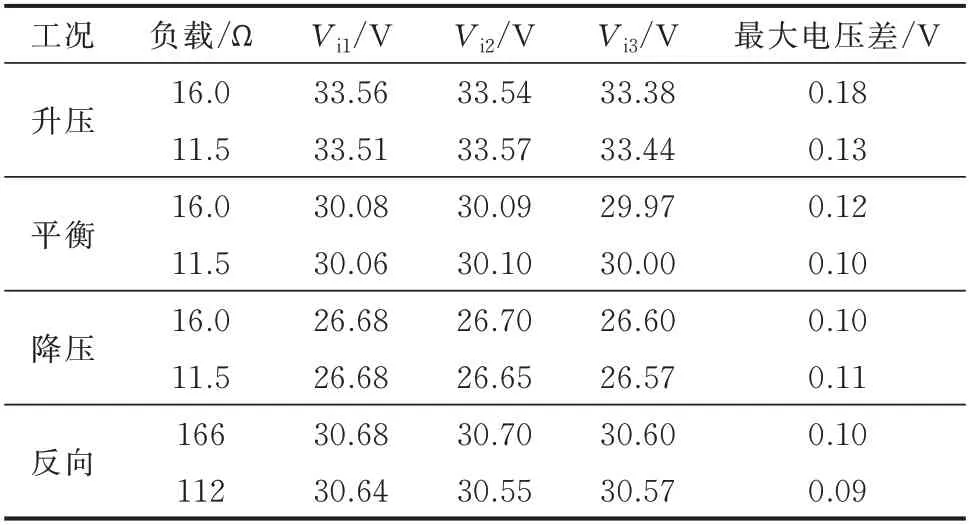
表1 SRBDCT 的IVS 结 果Table 1 IVS results of SRBDCT
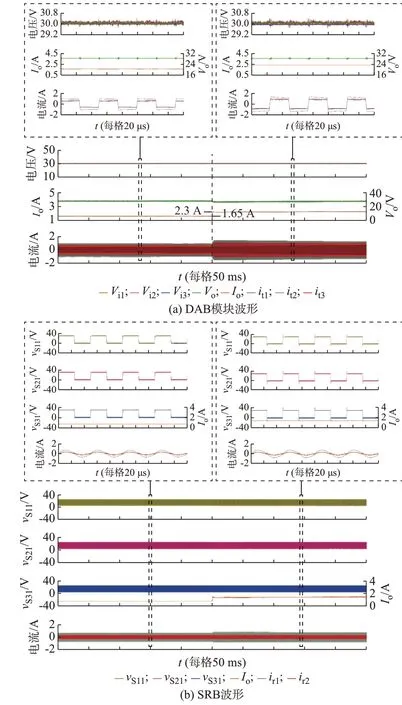
图3 Vi=90 V、负载从16 Ω 阶跃到11.5 Ω 时SRBDCT 的实验波形Fig.3 Experiment waveforms of SRBDCT when load changes from 16 Ω to 11.5 Ω and Vi=90 V
4.2 谐振支路应力实验与损耗仿真验证
IGBT S11的 两 端 电 压vS11、驱 动 信 号vgate以 及SRB1 的谐振电流ir1的实验波形见附录A 图A12。显然,当S11导通和关断时,电流ir1过零,因此,SRB不会导致IGBT 上开关损耗增加,与1.2 节分析一致。图4 展示了SRB 电流应力实验结果、输入桥IGBT 损耗标幺值。由图4 可以看出。计算曲线与实验和仿真结果均相符,因此,1.3 节与1.4 节中的分析得到验证。
(4) 当剪跨比、配筋率一定时,空心墩的承载力随着纵筋强度的提高而提高,延性变形能力随混凝土强度的提高而减小。

图4 SRB 电流应力和输入桥IGBT 损耗Fig.4 Current stress of SRB and IGBT loss of input bridge
SRBDCT 实验样机在正向功率传输条件下的效率曲线见附录A 图A13。由于该样机采用单移相调制方式,在低载条件下,升压和降压模式较难实现ZVS 软开关,其整体效率相较于电压平衡模式略低。
4.3 模块故障处理策略仿真验证
图5 为基于实验样机参数的模块故障处理仿真波形。

图5 DAB 模块2 故障处理仿真波形Fig.5 Simulation waveforms of fault handling of DAB module 2
当输入电压为90 V,故障模块2 切除后,输出电压控制在30 V,则其余模块的输入侧电压应力从30 V 提升到45 V,且模块2 所承担功率也由其余模块承担。模块2 切除后,2 条SRB 串联在一起,因此支路电流完全一致,如附录A 图A14(a)所示。当模块2 重新启动后,3 个模块重新均匀分压,且2 条SRB 分开平衡各自对应的DAB 模块,如图A14(b)所示,在故障切除过程中SRB 不会受到较大的冲击。因此,仿真结果验证了SRBDCT 的故障排除和恢复策略的可行性。后续研究中,可以在故障恢复时加入相应的启动策略来降低启动时的模块电流冲击。
4.4 IVS 复杂度对比
通过仿真和实验验证了所提出的SRBDCT 的特性,因此将其与传统的ISOP 型DCT 和基于VBC的DCT(VBCDCT)进行对比。表2 给出了3 种不同拓扑结构在m个模块下的比较。为了实现IVS,VBCDCT 和SRBDCT 都 增 加m-1 个SRB,但SRBDCT 节省了2m个开关器件。与VBCDCT 和SRBDCT 相 比,ISOP 型DCT 必 须 采 用m+1 个 电压传感器来采集所有模块的输入电压和输出电压,因此ISOP 型DCT 至少有m个电压反馈回路,从而增加了控制器的复杂度。 相反,VBCDCT 和SRBDCT 能够实现电压自平衡,因此,仅需要一个OVR 控制回路来调节输出电压,避免了ISOP 型DCT 中解耦变换带来的挑战。此外,虽然VBC 可以通过谐振电流实现零电流开关(zero current switching,ZCS),但无法消除VBC 开关造成的通态损耗Pcon和导通损耗Pon,而SRBDCT 则不会导致额外的开关损耗。综上所述,SRBDCT 在器件数量、开关损耗和控制复杂度方面具有显著的优势。
前些天,笔者回农村老家,和妻子孩子陪着母亲在场镇上逛了一圈,发现在挤满场镇街道两边的货摊上和商店里摆放的好些货品卖相不佳,特别是一些家庭生活必需品的质量堪忧,有些货品看起来已经非常老旧了,但仍旧摆放在摊位上和店里售卖,生意也自然冷冷清清,少有人驻足和问津。

表2 不同拓扑的比较Table 2 Comparison of different topologies
5 结语
本文所提出的SRBDCT 拓扑结构在不增加开关器件的前提下实现了串联输入侧的电压自平衡。同时,谐振支路不产生开关损耗,且故障模块切除后也不会破坏谐振支路的工作状态。相较于传统均压控制的ISOP 型DCT,电压自平衡结构能够降低控制器设计的难度,提高系统的可靠性,尤其对于模块参数差距较大的系统具有较高的实用性。
尽管SRB 不影响各模块的工作特性,也并不影响模块自身控制环路的特性,但增加的SRB 对DCT 的整体端口特性必然存在影响,尤其是串联侧的输入阻抗特性。下一步工作考虑建立SRBDCT的全阶小信号模型,推导该拓扑的阻抗特性,并研究与电网特性相匹配的控制策略。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

