利用智能电表量测数据的三相四线制配电线路参数辨识
熊尉辰,宋国兵,李 洋,宋晓林,黄璐涵,张 维,3
(1. 西安交通大学电气工程学院,陕西省西安市 710049;2. 国网陕西省电力公司营销服务中心,陕西省西安市 710054;3. 珠海许继电气有限公司,广东省珠海市 519000)
0 引言
随着用户对供电可靠性的要求逐步提高,及时排除低压配电网故障的方法日益受到关注[1]。但0.4 kV 低压配电线路多数位于建筑内部,为检修工作带来极大困难。大部分故障是由线路老化等引起的非突发性故障,常伴随线路阻抗增大的现象,及时掌握线路参数可实现非突发性故障预警及高危线路定位。实际的线路参数也是进行线损分析及潮流计算等研究的重要基础。而目前的相关研究通常利用线路长度及电阻率大致求取线路参数[2-3],但实际线路长度难以测量,且长时间运行后实际电阻率可能改变。因此,辨识低压配电线路参数具有重要意义。
现有的线路参数辨识方法大多应用于输电网及中压配电网。输电网及中压配电网的高级测量设备相对充足,可用于线路参数识别的信息较多[4-5],可以利用同步相量测量单元(synchrophasor measurement unit,PMU)进行同步相量测量[6-9],或利用录波设备记录数据[10-11]得到较为完备的相位信息或时域信息。
然而,在支路多、线路长度短的低压配电网中,缺乏高级测量设备[12],因此没有详细的相位和时域信息来源,无法借鉴输电网及中压配电网的线路参数计算方法。 但近年来随着高级量测体系(advanced metering infrastructure,AMI)的发展,智能电表逐渐成为低压配电网中广泛应用的测量设备,中国智能电表安装数量已超过5 亿只[13]。智能电表可获取用户带有时标的实时或准实时的计量值,如有功功率、无功功率、电压、电流等[14-15],能够为研究提供基础。
目前,对于低压配电线路参数的计算已有初步研究,但绝大部分文献假定三相负荷平衡,即不考虑中性线电流的影响,从而将网络简化为单相变压器带单相负载模型进行求解。
文献[16]假定三相平衡,建立了仅含一个分支节点的单相拓扑模型。文献[17]假定三相平衡及线路纯阻性,建立了单相拓扑纯电阻模型。文献[18-20]在文献[17]的基础上将线路电阻模型改进为阻抗模型,利用二次规划优化算法较为准确地计算了线路阻抗值,提出的方法依然建立在假定三相负荷平衡的基础之上,且利用该方法计算包含17个负荷节点、21 条线路的单相模型耗费2.75 h,不满足实际电力系统的计算需求。文献[21]利用粒子群优化算法计算了10 条线路的阻抗值,但所针对的模型为每个节点仅两条出线的单相拓扑模型,其计算方式不具有普遍性。文献[22]提出的方法是利用同一节点连接的两个电表测量值计算电压有效值之差,忽略电压降落的横分量,求解关于电阻及电抗的线性回归方程,但由于配电网中线路电阻远大于电抗,该方法的前提是负荷功率因数很高,而许多负荷的实际功率因数并不满足该前提。
低压配电网的三相不平衡现象普遍存在,中性线上的功率损耗不可忽略。因此,本文重点研究了线路和中性线的阻抗计算。
1)建立了一种三相四线制的低压配电线路阻抗模型,该模型较传统模型更加贴近工程实际;
2)提出了一种考虑中性线损耗的线路阻抗计算方法,该方法基于已知拓扑及智能电表提供的有限标量,分析各配电线路段的中性线损耗,利用线路阻抗、相位角、测量值之间的电气量关系进行求解;
3)编制了面对普遍拓扑形式的求解程序,输入拓扑及负荷信息,即可自动计算线路阻抗。
1 三相四线制低压配电网模型
为保证供电质量,低压配电变压器的供电半径很短,一般不超过500 m。对于低电压、短距离的配电线路,可忽略其分布电容的影响,采用集中参数阻抗模型进行等效。
实际的低压配电网一般为辐射状拓扑,负荷分段式接入。通常在一个表箱内装有各相的多块电表,先由各相干线向表箱供电,再经表箱进行分流,连接电表并入户。入户线一般较短,在建立模型时忽略其线路阻抗。同样地,与入户线并行分布的用户段中性线也较短,忽略其线路阻抗。一个表箱所包含的负荷电流先经过自身的用户段中性线及同一段中性线干线进行回流,再与上级中性线干线构成回路。所建立的一种三相四线制低压配电网模型如图1 所示。要指出的是,图1 只是拓扑形式举例,其他拓扑形式均可由此推出。

图1 三相四线制低压配电网模型Fig.1 Model of three-phase four-wire low-voltage distribution network
为简化起见,仅在图1 中标出了A 相及中性线的相关标识。
1)将变压器等效为三相交流电源,ZAs为A 相电源 等 效 阻 抗;U̇As、İAs分 别 为 变 压 器 出 口 处A 相 电压、电流相量。
2)电表的量测均为相对于中性线的量测,相应地,A0、N0分别为A 相、中性线上的总表测点,共同进行A 相相电压的测量。A1,A2,…,An为A 相干线上的分支节点,其中n为干线上分支节点的个数。在实际配电网中,必须有中性线与相线并行分布,从而形成电流回路,所以中性线随相线的分支而分支,中性线上的对应分支节点为N1,N2,…,Nn。将A 相的总表测点及分支节点表示为Ai,其中i=0,1,…,n;将中性线上的总表测点及分支节点表示为Nf,其中f=0,1,…,n。
3)ZL,A,i为 节 点Ai后 的 一 级 干 线 阻 抗,因A0的存 在,ZL,A,i为 图1 中A 相 从 左 至 右 的 第i+1 条 一 级干 线 阻 抗;Zd,A,j为 图 中A 相 从 左 至 右 的 第j条 二 级干线阻抗。其中,因节点A0为总表测点,其下无分支负荷,所以j不可取0;又因节点An后有两条通向分支负荷的干线,最后一条干线既可作为一级干线ZL,A,n,也 可 作 为 二 级 干 线Zd,A,n+1,图 中 用ZL,A,n(Zd,A,n+1)的形式表示该线路,所以j可取n+1。综上,j=1,2,…,n+1。
同理,ZN,f为节点Nf后的一级中性线阻抗,因N0的 存 在,ZN,f为 图1 中 从 左 至 右 的 第f+1 条 一 级 干线阻抗;Zn,r为图中从左至右的第r条二级中性线阻抗,其中r=1,2,…,n+1。İN,f为第f+1 条一级中性线电流相量,即流过阻抗ZN,f的电流;İn,r为第r条二级中性线的电流相量,即流过阻抗Zn,r的电流。同理,对于ZL,A,n(Zd,A,n+1),图中也用ZN,n(Zn,n+1)的形式 表 示 最 后 一 条 中 性 线,用İN,n(İn,n+1)表 示 该 线 路的电流。
4)İA,1,1、U̇A,1,1分 别 为A 相 二 级 干 线Zd,A,1下 所连接的第1 个负荷的电流、电压相量。依此类推,将A 相 第j条 二 级 干 线Zd,A,j下 所 连 接 的 第k个 负 荷 的电 流、电 压 相 量 分 别 记 为İA,j,k、U̇A,j,k,其 中,k=1,2,…,m(m为二级干线Zd,A,j下所连接负荷的个数)。
B、C 相的相关物理量与A 相类似,不再赘述。将A、B、C 相线上的第i+1 个节点表示为αi,其中α代表A、B、C 三相。
已知量及待求量如下:
1)已知量为智能电表测得标量
(1)在变压器出口测得:α相的电源电压有效值Uαs、电流有效值Iαs、有功功率Pαs、无功功率Qαs;
(2)将α相第j条二级干线下的第k个负荷记为αj,k,在 负 荷αj,k处 测 得:负 荷 的 电 压 有 效 值Uα,j,k、电流有效值Iα,j,k、有功功率Pα,j,k、无功功率Qα,j,k。
2)待求量为各条线路阻抗
(1)相线阻抗:α相一级干线阻抗ZL,α,i,α相二级干线阻抗Zd,α,j;
(2)中性线阻抗:与一级干线并行分布的一级中性线阻抗ZN,f,与二级干线并行分布的二级中性线阻抗Zn,r。
2 线路参数计算方法
智能电表所提供的数据种类及数据量虽已大幅增加,但仍只包含标量信息,不含相位信息。在参考相位未知、拓扑含有大量中间节点的情况下,如何利用智能电表提供的标量数据进行相量运算,是本文重点解决的第一个问题。
在低压配电网中,中性线随着相线的分支而分支,中性线电流随着负荷电流的改变而改变,且各段中性线上的电流、损耗及压降均不相同。在三相四线制拓扑模型中,中性线功率损耗是区别于单相模型的根本之处。如何处理中性线功率损耗与各负荷之间的关系是本文重点解决的第二个问题。
下面以图1 所建立的模型为例进行计算原理说明,对于其他形式的辐射状拓扑,本方法依然适用。
2.1 线路功率分布的求取
1)求取中性线电气量
首先给出线路阻抗初值,根据拓扑连接方式确定中性线电流初值、中性线阻抗上的压降,再计算中性线功率损耗的来源及大小。
初值选取方式分为3 种:1)若线路长度及电阻率等相关参数均有记录,可计算得到线路阻抗并将其作为初值;2)若线路长度及电阻率等相关参数未知,此时将线路阻抗初值设定为0;3)将阻抗初值设定为0 时求解得到的阻抗新值作为下次计算的阻抗初值。
利用智能电表测得的有功和无功功率,由式(1)计算电源处及负荷处的功率因数角:
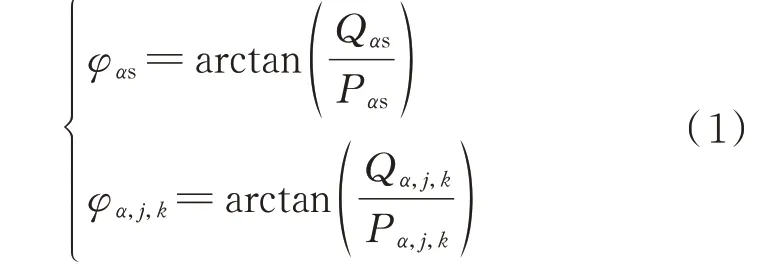
式 中:φαs为α相 电 源 处 的 功 率 因 数 角;φα,j,k为 负 荷αj,k的功率因数角。
假设A 相所有端点的电压相量相角初值均为0°、三相电压相量相角初值互差120°,将求得的功率因数角代入式(2)求三相负荷电流初值:

式 中:İA,j,k、IA,j,k、φA,j,k分 别 为A 相 第j条 二 级 干 线 下第k个负荷的电流相量、电流有效值、功率因数角;İB,j,k、IB,j,k、φB,j,k分 别 为B 相 第j条 二 级 干 线 下 第k个负 荷 的 电 流 相 量、电 流 有 效 值、功 率 因 数 角;İC,j,k、IC,j,k、φC,j,k分 别 为C 相 第j条 二 级 干 线 下 第k个 负 荷的电流相量、电流有效值、功率因数角。
假设三相电压相角初值互差120°,包含两层含义:1)三相电源电压相角初值互差120°;2)三相负荷电压相角初值互差120°。文献[23]实验证实,在一般工况下,当电源处三相电流不平衡度达到15%时,电源处三相电压相位差偏离120°的范围在0.1°左右;当电源处三相电流不平衡度达到30%时,电源处三相电压相位差偏离120°的范围在0.3°左右。有关规程规定,配电变压器出口处的三相电流不平衡度应小于10%,则三相电源电压相位差偏离120°的范围应更小,因此基本可接受该假设。从必要性上来看,所需中性线电流为三相电流之和,要实现中性线电流的计算,必须要依靠电源电压相位的关系来寻找全局电气量的统一参考相位。但由于无法测得电源电压相角,只能通过假设电源电压相位互差120°进行后续计算。所有负荷电压相角会随着后续的迭代计算而逐步逼近真实值。
中性线电流为其上游连接的所有负荷电流之和。由中性线与负荷支路的连接方式可得中性线电流初值,根据给出的线路阻抗初值可得中性线阻抗压降,利用式(3)求取:
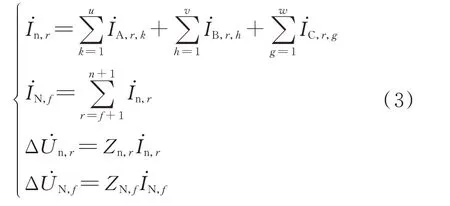
式 中:İA,r,k为A 相 第r条 二 级 干 线 下 第k个 负 荷 的 电流;İB,r,h为B 相 第r条 二 级 干 线 下 第h个 负 荷 的 电流;İC,r,g为C 相 第r条 二 级 干 线 下 第g个 负 荷 的 电流;ΔU̇n,r为 第r条 二 级 中 性 线 阻 抗Zn,r上 的 压 降;ΔU̇N,f为第f+1 条一级中性线阻抗ZN,f上的压降;u、v、w分别为第r条二级中性线上游所连接的A、B、C相负荷的个数。
用式(4)计算经由负荷αj,k流入中性线的功率:
式 中:ΔSn,r,α,j,k为 经 由 负 荷αj,k流 入 第r条 二 级 中 性线的功率;ΔSN,f,α,j,k为经由负荷αj,k流入第f+1 条一级中性线的功率。
2)推算二级干线始端功率
二级干线始端功率包含两部分:(1)流入其下连接的所有负荷节点的功率之和;(2)二级干线本身的功率损耗。通过式(5)进行计算:

式 中:Sd,α,j为α相 第j条 二 级 干 线 的 始 端 功 率;Sα,j,k为流入负荷αj,k的功率;ΔSd,α,j为α相第j条二级干线的功率损耗。
流入负荷的功率包含三部分:(1)负荷本身消耗的功率;(2)经由该负荷流入下游一级中性线的功率之和;(3)经由该负荷流入二级中性线的功率。将测量所得负荷有功、无功及由式(4)计算得到的中性线损耗代入式(6),得到流入负荷αj,k的功率:
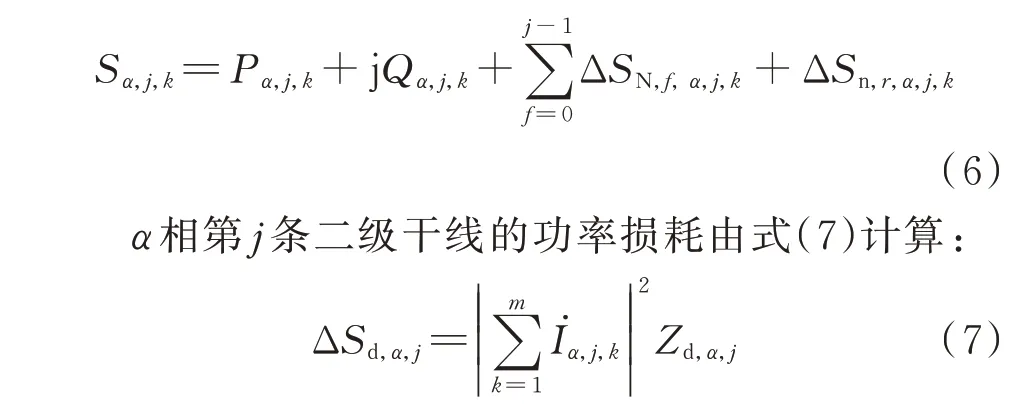
3)推算一级干线始端功率
一级干线始端功率包含三部分:(1)流入其下游连接的所有负荷的功率之和;(2)其下所有二级干线的功率损耗之和;(3)其下所有一级干线及其本身的功率损耗之和。通过式(8)求取:

式 中:SL,α,i为α相 第i+1 条 一 级 干 线 的 始 端 功 率;ΔSL,α,λ为α相第λ+1 条一级干线的功率损耗,其中λ=i,i+1,…,n-1;在 该 式 中j=i+1,i+2,…,n+1。
节点αi后的一级干线功率损耗由式(9)计算:

依此类推,求得所有线路的功率分布,为后续计算电压、电流相量新值做准备。
2.2 电气量的推算及更新
1)从电源侧向负荷侧推算电压电流相量以A 相电源电压相量为参考,利用线路功率分布,从电源侧向负荷侧推算节点电压相量、线路电流相量,如式(10)所示。最后一个负荷支路编号较为特殊,但计算方法相同,以下不做特殊说明。
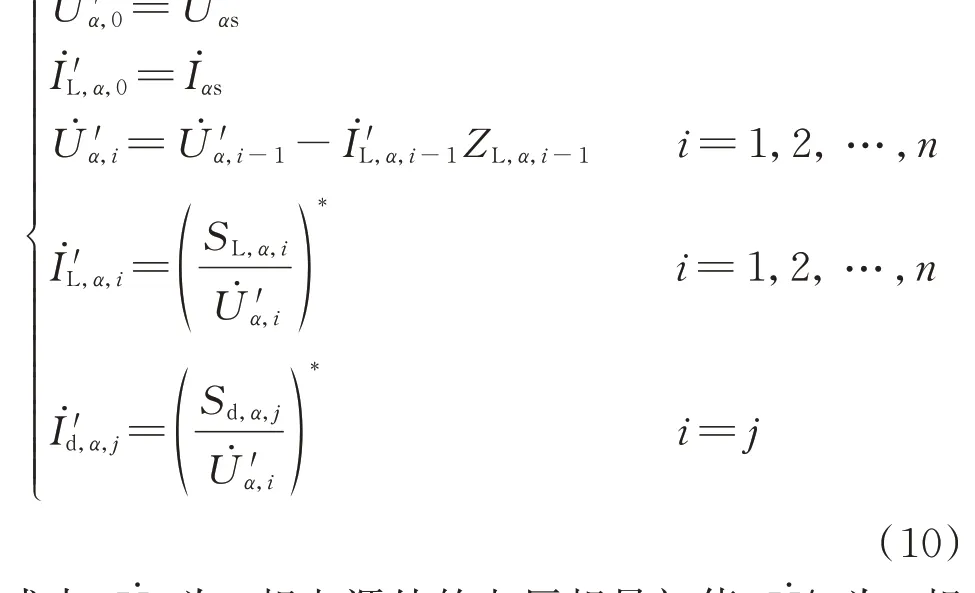
式中:U̇αs为α相电源处的电压相量初值;U̇'α,0为α相电 源 处 的 电 压 相 量 新 值;İ'L,α,0为α相 电 源 处 的 电 流相 量 新 值;İαs为α相 电 源 处 的 电 流 相 量 初 值;U̇'α,i为节 点αi的 电 压 相 量 新 值;İ'L,α,i为α相 第i+1 条 一 级干 线 的 电 流 相 量 新 值;İ'd,α,j为α相 第j条 二 级 干 线 的电流相量新值。
2)求取新的负荷电压电流相量
利用式(11)提取负荷αj,k的电流相量相位角:

式中:θα,j,k为负荷αj,k的电流相位角。
结合提取的电流相位角赋予测量所得的负荷电流有效值,形成新的负荷电流相量;并利用式(1)中求得的负荷功率因数角,计算出新的电压相位角,结合测量得到的负荷电压有效值,以形成新的负荷电压相量。

式 中:İ'α,j,k为 负 荷αj,k的 电 流 相 量 新 值;U̇'α,j,k为 负 荷αj,k的电压相量新值。
式(11)求出了电流相量在统一参考相位下的相位角,式(12)通过利用测量所得有效值再次约束了电气量幅值。
3)求取中性线电流相量新值
根据拓扑连接方式及式(13)求取更新的中性线电流相量:
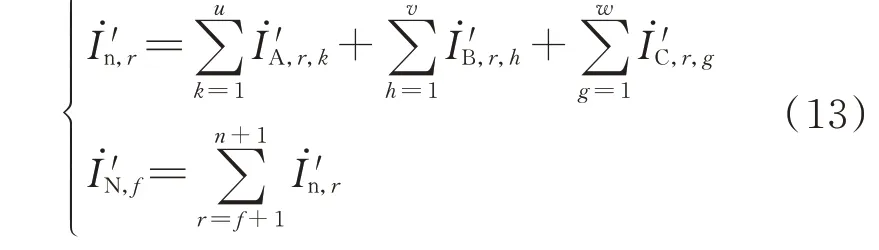
式 中:İ'n,r为 第r条 二 级 中 性 线 的 电 流 相 量 新 值;İ'N,f为 第f+1 条 一 级 中 性 线 的 电 流 相 量 新 值;İ'A,r,k为A 相第r条二级干线下第k个负荷的电流相量新值;İ'B,r,h为B 相 第r条 二 级 干 线 下 第h个 负 荷 的 电 流 相量 新 值;İ'C,r,g为C 相 第r条 二 级 干 线 下 第g个 负 荷 的电流相量新值。
依此类推,求得所有电压、电流相量的新值,为后续线路阻抗新值的求解做准备。
2.3 形成方程组并求解
1)基于基尔霍夫电压定律列写方程式
列写A、B、C 相线与中性线间关于电源电压相量、待求的线路阻抗新值、线路电流相量、负荷电压相量的回路电压方程式。
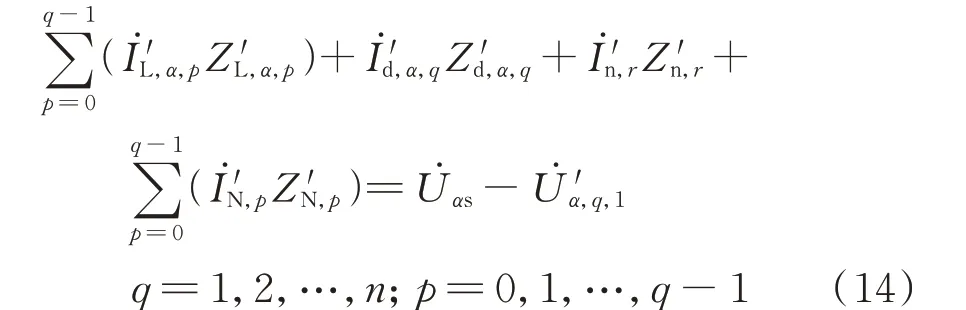
式 中:İ'L,α,p为α相 第p+1 条 一 级 干 线 的 电 流 相 量 新值;Z'L,α,p为α相第p+1 条一级干线的阻抗新值;İ'd,α,q为α相第q条二级干线的电流相量新值;Z'd,α,q为α相第q条二级干线的阻抗新值;Z'n,r为第r条二级中性线的阻抗新值;İ'N,p为第p+1 条一级中性线的电流相量新值;Z'N,p为第p+1 条一级中性线的阻抗新值;U̇'α,q,1为α相第q条二级干线下第1个负荷的电压相量新值。
在式(14)中,特定的q值代表特定的回路,该回路 中 的 二 级 干 线 阻 抗Zd,α,j的 下 标j决 定q的 取 值。由最后一个负荷支路形成的回路电压方程与式(14)相似,仅需将等号左边第2 项及等号右边第2 项下标中的q换为n+1 即可。
对于特定的q值,可得到已知量为电压、电流相量,待求量为线路阻抗新值的关系式,利用该式及多个时间断面下的测量值形成方程组。
2)利用最小二乘法求解超定方程组
通常求解一个含有γ个未知量的方程式,需要γ组非线性相关的数据形成方程组。但在该情形下的方程组中,作为已知量的各电气量均由假定的线路阻抗初值计算而来,仅依靠γ个方程无法求出满足要求的未知量,因此需要尽可能多的测量数据来约束方程的求解方向,从而形成超定方程组。对该方程组的求解过程即为利用测量所得标量对线路阻抗初值的修正过程。
最小二乘法因其便于理解、计算方便等特点而被广泛应用,本文采用最小二乘法求解线性回归方程式的系数。对于式(14)中不同q值对应的关系式,将各个采样时刻的测量值代入,可得到形如AZ'=b的线性方程组。其中,A为多个时刻下的电流相量新值形成的已知系数矩阵;Z'为待求的线路阻抗新值形成的未知量向量;b为多个时刻下的电压相量新值形成的已知向量。

式中:上标(1),(2),…,(t)代表不同的采样时刻。
利用复数域内的最小二乘公式求解Z':
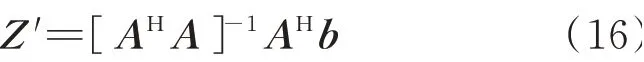
式中:AH为矩阵A的共轭转置矩阵。
需要说明的是,本文采用递进求解的方法进行计算。将q=j时方程(即α相第j条二级干线所在回路与电源形成的回路电压方程)求出的各个线路阻抗新值作为已知量代入q=j+1 时的方程,再利用最小二乘法求解其他未知量(此时j=1,2,…,n)。
以q=1、q=2 分别举例说明。当q=1 时,式子中包含的线路阻抗新值为:Z'L,α,0、Z'd,α,1、Z'n,1、Z'N,0;利用多组测量值形成超定方程组后可求解。当q=2时,式 子 中 包 含 的 线 路 阻 抗 新 值 为:Z'L,α,0、Z'L,α,1、Z'd,α,2、Z'n,2、Z'N,1、Z'N,0;其 中Z'L,α,0、Z'N,0的 值 在q=1 的式子中已经求出,可直接应用于q=2 的式子中,进而求解Z'L,α,1、Z'd,α,2、Z'n,2、Z'N,1。
这种计算方式减少了每步未知量个数,缩短了求解时间,并且所采用的电气量均为在全局量测下的推算值,计算得到的线路阻抗是在后续迭代过程中不断被全局量测约束后的求解结果,不会增大计算误差。
待求解出一组完整的线路阻抗新值后,将该组阻抗新值作为初值代入式(1)至式(11),形成迭代求解过程。当第β+1 次求解出的线路阻抗与第β次求解出的阻抗差值的二范数不超过设定范围时,停止迭代,输出计算结果。设置停止迭代的条件为:

本文将测量所得有效值作为约束进行迭代计算,使计算结果逐步逼近线路阻抗真值。每次迭代修正量不大,可能数千次迭代后计算结果才可满足要求。但每次迭代均为线性回归方程组的求解,计算速度很快,因此总计算时间较短。
3 数据质量问题处理方法
由于量测数据可能出现各种质量问题,在计算之前要对所采集的数据进行相应处理。以下针对几种常见问题提出解决方法。
3.1 采样数据部分缺失
受到通信等因素的影响,会出现某些时刻下台区的电表数据不能100%采集的情况,若继续利用缺失数据的数组进行计算,将产生较大计算误差,因此要剔除此类数组。
3.2 空房支路
若在采样时间跨度内某用户负荷电流为零,则无法反映该用户所在支路与网络的电气联系,该支路参数不可求取。仍按照初始拓扑结构进行回路电压方程的求解,会导致求解错误。此时,可根据用户电流数据更改初始拓扑结构,去除空房支路,即空房支路的线路阻抗不予求取。
3.3 智能电表时钟偏差及量测数据误差
由于智能电表本身的时钟偏差,在同一时刻采样得到的各电表量测值可能不是完全同步的。实际工程中,可控制各个电表之间的时钟偏差在1 min以内,若在此时钟偏差范围内负荷不波动或波动不大,则数据质量仍然较高。但智能电表的数据冻结频率普遍为15 min/次,难以保证每个负荷在采样时刻1 min 内没有大幅波动。工程中可在台区变压器测点(总表处)安装总用电量采样装置,该装置可提供每秒的台区总用电量。依此提出数据筛选方法:根据总用电量在采样时刻1 min 内的波动程度进行数据筛选,将总用电量波动较大的对应数据组剔除。该方法可在一定程度上减轻智能电表时钟偏差对计算结果的影响。将多个采样周期的计算结果取平均值,可进一步减小其对计算产生的影响。由于电表本身存在测量误差,该误差会随着负荷电流大小及温度等因素而改变,将多个采样周期下的计算结果取平均值也可减小测量误差的影响。
4 面对普遍拓扑形式的求解程序
为方便算法应用,编制了面向普遍三相四线制拓扑形式的求解程序。在程序中输入各相负荷信息(包括拓扑信息及量测数据),可生成算法所需拓扑矩阵,经计算即可输出各条线路首末节点编号及对应的线路参数。
4.1 算法所需矩阵的生成
1)节点编号
为了让各种形式的辐射状拓扑均可在同一程序中求解,给出统一的节点编号规则:先编号电源节点及中间节点,后编号负荷节点,节点编号沿着支路延伸方向依次递增;当三相拓扑节点个数不同时,取其并集拓扑进行编号。
2)输入各相线路的拓扑信息
输入的拓扑信息包括:(1)各相线路首末节点;(2)并集拓扑的总节点个数n;(3)并集拓扑的电源节点及中间节点个数m。
据此分别形成三相初始拓扑矩阵YA、YB、YC,其维数均为m×n,首末节点(对应初始拓扑矩阵横纵坐标)对应的位置元素为1,其他位置元素为0。
3)输入量测数据及生成所需矩阵
由提出的算法可知,所需拓扑矩阵主要包括:(1)各相需要求取阻抗的线路拓扑矩阵;(2)中性线拓扑矩阵;(3)各段中性线上游连接的负荷节点编号所形成的元胞矩阵;(4)各个负荷节点连接的下游中性线编号所形成的元胞矩阵;(5)各条线路下游连接的负荷节点编号所形成的元胞矩阵;(6)各条干线下游连接的相线编号所形成的元胞矩阵;(7)从各个负荷节点追溯至电源节点历经的相线编号及中性线编号所形成的元胞矩阵。
其中,线路的编号方式为:将各相需要求取阻抗的线路拓扑矩阵中的非零元素按照从上至下、从左至右的规律找出,并利用其横纵坐标生成新的首末节点编号向量,如此便不拘泥于输入节点编号时的元素顺序,所得到向量的元素位置序号为线路编号,可用于后续求解。以两个矩阵的生成为例。
以仿真算例中图2(b)的B 相拓扑为例,生成B相需要求取阻抗的线路拓扑矩阵。B 相的负荷节点9、14 不存在,在程序中输入编号时将这两个节点所在支路排除。再根据输入的负荷电流数据判断是否存在空房支路,若存在,则将该负荷节点所在支路排除即可。

图2 算例简化拓扑图Fig.2 Simplified topology diagram of calculation example
输入的B 相线路首末节点编号向量为:
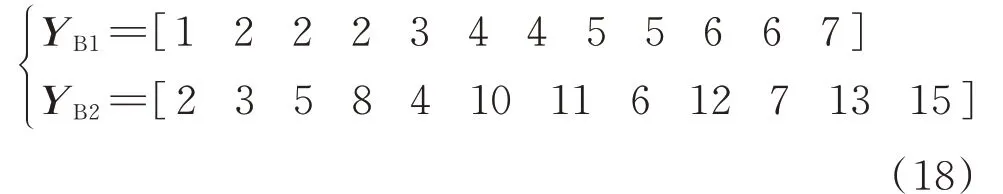
式中:YB1为B 相线路首端节点形成的向量;YB2为B相线路末端节点形成的向量。
同时,输入并集拓扑的所有节点个数n=15、电源及中间节点个数m=7,据此生成B 相初始拓扑矩阵YB,如式(19)所示。
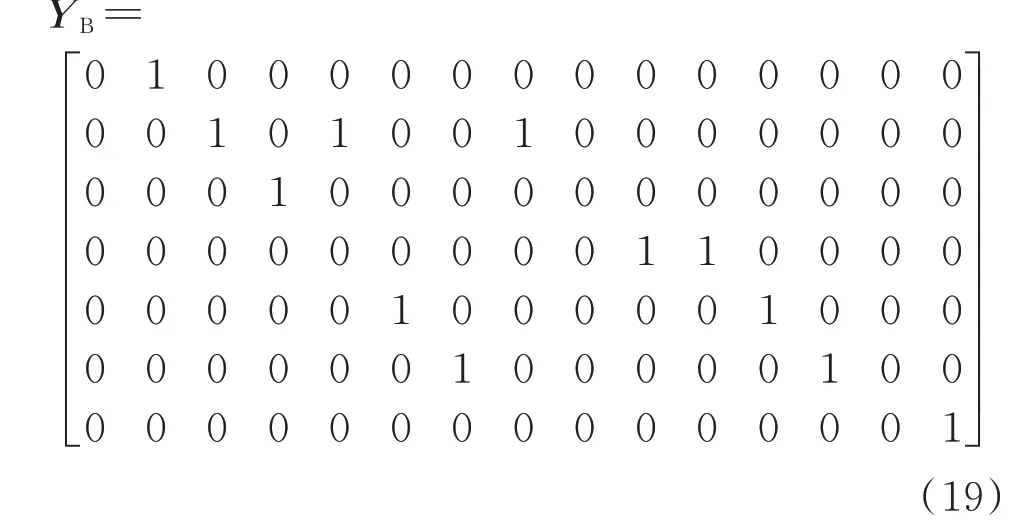
而中间节点3 不存在于B 相相线上,此时只能求取B 相线路2-3(首端节点编号-末端节点编号)、3-4 的阻抗之和,即B 相线路2-4 的阻抗;同样地,中间节点7 不存在于B 相相线上,只能求取B 相线路6-7、7-15 的阻抗之和,即B 相线路6-15 的阻抗。假设此时无空房支路存在,将YB调整为需要求取阻抗的B 相线路拓扑矩阵Y'B。

再举例说明如何生成各条干线下游连接的相线编号所形成的元胞矩阵。将Y'B中的非零元素按照从上至下、从左至右的顺序找出,得到B 相待求阻抗相线的首末节点编号向量。
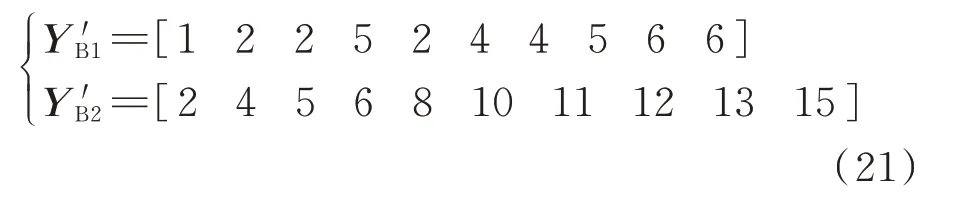
式中:Y'B1为需要求取阻抗的B 相线路首端节点形成的向量;Y'B2为需要求取阻抗的B 相线路末端节点形成的向量。
需要求取的B 相第l条线路的首、末节点编号分别对应于Y'B1、Y'B2中的第l个元素,其中l=1,2,…,10。通过式(21)中末节点与首节点对应相等的元素位置编号,可确定某条干线下游连接的相线元素。
当l=3 时,即对于首节点编号为2、末节点编号为5 的干线,其下连接的相线有:首节点为5、末节点为6 的相线,对应l=4;首节点为5、末节点为12 的相线,对应l=8;首节点为6、末节点为13 的相线,对应l=9;首节点为6、末节点为15 的相线,对应l=10。
依此类推,可得到B 相干线(干线末端节点编号Y'B2(l)≤7)下游连接的相线编号元胞矩阵为:LB=[[2 3 … 10],[6 7],[4 8 9 10],

同理,可生成计算所需的其他拓扑相关矩阵,进而应用于后续求解。
4.2 算法流程
所编制的算法程序可变换出多种拓扑矩阵,并按照所提算法求取线路阻抗,求解流程如图3所示。
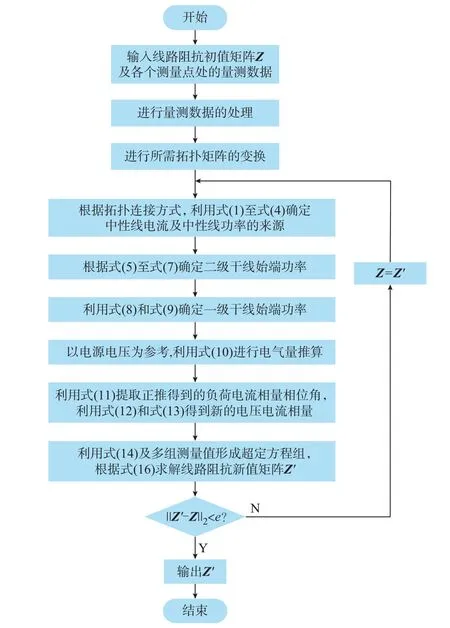
图3 算法流程图Fig.3 Flow chart of algorithm
5 算例分析
5.1 算例拓扑
以含有20 个负荷节点、47 条线路(含34 条相线待求支路、13 条中性线待求支路)的三相四线制拓扑为例进行验证。
由于实际中三相的负荷一般并不对称,所举出的算例拓扑采用不对称形式。为简明,略去线路阻抗模型以及负荷模型,分别表示A、B、C 三相及中性线的拓扑连接方式,如图2(a)、(b)、(c)、(d)所示。
相应的节点编号规则已在上文予以介绍。图2中,为区分节点类型,将电源节点及中间节点用红色数字标出,将负荷节点用蓝色数字标出。图2 中,节点1 处的圆圈代表变压器出口处测量点,其他圆圈代表负荷处测量点,圆圈旁的数字代表节点编号。B 相的9、14 号负荷不存在,C 相的10、14 号负 荷不存在,为便于观察,将不存在的负荷支路用虚线表示。需要说明的是,由于14 号负荷处仅有A 相负荷,该处的中性线电流与相线电流相同,只能求出中性线阻抗与相线阻抗之和,在此算作求取该处负荷支路的相线阻抗。
5.2 仿真验证
为了说明算法本身的有效性、假设条件和数据质量产生的影响,设置以下算例:
1)在5.3 节中设置了不考虑电源内阻(即电源电压互差120°)、数据质量高的仿真计算,以验证理想状态下算法本身的性能。
2)在5.4 节中设置了考虑电源内阻及数据质量存在问题时,即非理想状态下的相关仿真计算,以反映假设条件及可能存在的数据质量问题对计算结果产生的影响。其中,对于5.4 节仿真计算中的原始数据设置条件:(1)在每个采样周期内选取不同的负荷,将所选取负荷的测量数据设为空,以模拟数据缺失;(2)在每个采样周期内选取不同的负荷,将所选取的负荷支路断开,以模拟空房支路;(3)在每个采样周期内,对仿真中的部分负荷进行调整,将调整前的一半测量数据及调整后的一半测量数据互补作为同一个时刻下的采样数据,以模拟数据筛选过后仍存在的时钟偏差现象;(4)在每个采样周期内,给各个负荷处测得的有功功率、无功功率、电压有效值、电流有效值各添加误差标准差为3%的随机测量误差。
5.3 理想状态下的算法性能验证
为验证算法本身的有效性及精确性,将仿真中的α相电源内阻Zαs置零,采用无测量误差、无时钟偏差的量测量进行求解。经计算,发现由本文方法得到的线路阻抗计算值与仿真模型中的线路阻抗设置值相同。表1 列出了部分计算结果。

表1 理想状态下的线路阻抗计算结果Table 1 Calculation results of line impedance under ideal conditions
由表1 可知,算法本身的计算精度很高。
为探究线路阻抗初值对迭代次数、迭代时间及算法收敛性的影响,线路阻抗初值设定如下:
1)线路阻抗初值比仿真模型中设定的线路阻抗值 分 别 减 少(0.01+j0.01) Ω、(0.02+j0.02)Ω、(0.03+j0.03)Ω,模拟根据已知的线路长度与电阻率等相关参数计算出的阻抗初值。
2)线路阻抗初值设为0 Ω,对应线路长度与电阻率等相关参数未知时,初值选取没有基准的情况。
3)线路阻抗初值设为真实阻抗值的5、7、10 倍,探究阻抗初值的选取对于算法收敛状况的影响。
每次计算采用一个采样周期内的数据,每个采样周期含有48 组量测值。进行10 次计算,记录迭代次数及迭代时间。当收敛精度e=10-10时,平均迭代次数、平均迭代时间、收敛状况如表2 所示。

表2 线路阻抗初值对计算的影响Table 2 Effect of line impedance initial value on calculation
从表2 看出,初值与真实值偏离越大,所需的迭代次数及迭代时间越长,且在较大的初值选取范围内算法收敛。从总体上看,迭代求解该含有47 条线路的三相算例用时很短,相较于文献[19]中耗时2.75 h 计算包含21 条线路的单相模型所采用的二次规划优化算法,计算速度大幅提高。
5.4 非理想状态下的仿真计算
将仿真模型中的电源内阻Zαs设置为0.001 Ω,将计算所需的线路阻抗初值设置为普遍适用的0 Ω。每次计算采用一个采样周期内的数据,每个采样周期含有48 组量测值,进行10 次计算,记录线路阻抗平均值。当设置收敛精度e=10-10时,计算结果的平均值及电阻与电抗的误差百分数如表3 所示。为节省篇幅,只列出部分线路的计算结果,其中保留了误差最大项。
由表3 可以看出,在电源含有内阻、考虑数据质量时,电阻与电抗计算平均值的误差最大值分别为6.20%、7.96%。与表1 对比可知,电源不对称及量测数据质量对算法计算精度有一定影响。
但在线路阻抗增大(线路老化)时,计算误差并不妨碍对老化线路的确定,且阻抗增大后,计算相对误差将减小。将表3 中计算误差较大的线路阻抗实际值增大,以模拟线路老化现象,计算结果如表4 所示。由表4 可知,利用线路阻抗计算结果可确定老化的高危线路,及时予以更换能够降低运维成本、提高供电可靠性。

表3 线路阻抗计算结果平均值Table 3 Average value of line impedance calculation results

表4 老化线路阻抗计算结果平均值Table 4 Average value of calculation results for impedance of aging lines
与此同时,该算法程序在计算过程中可得到工程中无法测量的线路电流,能用于提高线损分析的准确度。以中性线电流为例,在一个采样时刻下,中性线电流有效值的测量值与计算值及误差百分数如表5 所示。由表5 可见,此时计算值的最大误差为2.20%,且中性线电流计算结果也可用于指导低压配电网三相负荷不平衡的改善工作,进一步减少线路损耗。

表5 中性线电流测量值与计算值Table 5 Measured and calculated values of neutral line current
6 结语
低压配电网作为向用户供电的最后一环,其运行状态直接影响供电质量。智能电表是广泛应用于低压配电网末端的测量装置,利用其提供的数据进行线路参数辨识研究,对掌握电网运行状态、降低运行成本等具有重要意义。本文提出了应用于三相四线制低压配电网的线路参数计算方法,与已有的单相拓扑参数求解方法相比,具有模型贴合度高、求解速度快、精度高的优势,更符合工程应用需求。
为进一步减小计算误差,未来可在所计算台区的变压器二次侧安装相位测量元件,以弥补本文假设条件上的不足。此外,无论采用何种算法,量测数据的准确度均为影响计算结果的重要因素,目前在线路参数未知的条件下暂无十分有效的数据处理方法。今后可在完善数据处理方法的同时,探索提高设备量测准确度的途径。
本文研究得到珠海市产学研合作项目(ZH22017001200158PWC)资助,特此感谢!

