发动机稀燃条件下纳秒脉冲等离子体助燃甲烷/空气的数值模拟

班杨杨，张 帆，钟生辉，朱家健

(1.天津大学内燃机燃烧学国家重点实验室，天津 300072；2.国防科技大学高超声速冲压发动机技术重点实验室，长沙 410073)

内燃机的发展极大地改善了人类的出行方式，随着排放法规的日趋严格，亟需发展新型燃烧技术以实现高效清洁燃烧.均质压燃(HCCI)是目前最具前景的燃烧方式之一.HCCI 发动机通常采用高压缩比、稀燃等技术实现高效燃烧，但在高负载工况下，难以控制放热率和点火正时，导致运行工况狭窄[1].稀燃技术可有效改善热效率，提高燃油经济性，减少NOx排放，但滞燃期延长，限制了火焰传播速度.天然气被认为是最有潜力的发动机替代燃料，其主要成分是甲烷，可以用于火花点火的均质混合气天然气发动机[2].破坏甲烷的C—H 键需要较高的点火能量，火花放电产生的平衡等离子体，形成局部高温区[3]点燃混合气，不具有化学选择性且基电极的存在限制了高温区范围，大部分能量被用于加热电极，导致火花塞放电需要消耗更高的能量点燃天然气.此外，可以采用新型点火技术，如纳秒脉冲点火系统产生非平衡等离子体实现助燃[4-5].纳秒脉冲放电能克服传统火花点火系统面临的大多数限制[5]，是在技术上用于点燃稀燃料/空气混合气的可行的点火系统.

大量工作对比了平衡和非平衡等离子体助燃，例如Adamovich 等[6]通过研究平衡加热和非平衡放电助燃低温C2H4/空气，发现后者产生了较多的自由基，使点火时间缩短了两个数量级，点火温度降低300 K.文献[7]表明，沉积到非平衡等离子体的能量(50 mJ/cm3)导致点火温度比自燃降低600 K，而如果这些能量全部用于加热混合气(类似于平衡等离子体)，点火温度只能降低20 K.

在非平衡等离子体中，电子温度远高于中性气体的温度，只有少部分沉积能量用于加热混合气.电子在外加电场的作用下，与中性气体分子发生非弹性碰撞，产生大量活性粒子.激发态粒子的活性远高于其基态，对于同一个反应，激发态的参与可降低反应活化能，提高化学反应速率.Uddi 等[8]通过双光子激光诱发荧光技术，发现氧原子是等离子体点火、提高火焰传播速度的关键粒子.除了具有化学选择性，非平衡等离子体中电子通过非弹性碰撞离解大分子，可增强扩散输运效应；另外，放电过程中产生的离子风或电离波可增强对流输运效应[9-10].描述非平衡等离子体动力学的模型主要有3 种：①基于统计理论发展了动理学模型[11]；②流体模型[12-13]，将等离子体视为导电流体，求解动力学方程和麦克斯韦方程组；③全局模型即零维模型[14]，基于玻尔兹曼二项近似求解电子能量分布函数.大量工作基于零维模型开展，模拟结果表明，在非平衡放电过程中，O 原子[8,15]、单态氧原子O(1D)[16]和单态氧分子[17]是等离子体助燃的关键组分，Starik 等[18]证实了单态氧分子对HCCI 发动机的燃烧增强作用比O 原子更显著.空气中的放电模拟表明，激发态N2与O2的淬灭反应生成了大量有助于燃烧的O 原子[19].而且，等离子体可将生成的HCO 直接分解，降低HCO 对H 原子的消耗[20].

非平衡等离子体可通过电晕放电[21]、纳秒脉冲放电[22]等方式产生.电晕放电或纳秒脉冲放电与火花塞放电的区别在于前两者电子温度远高于气体温度，产生非平衡等离子体形成体积点火源，主要通过化学动力学效应助燃，还可以减小刘易斯数，提高火焰传播速度；而火花塞放电时电极间形成高温热电弧，产生平衡等离子体，主要通过热效应点燃混合气.文献[23]实验对比了火花放电和电晕放电，结果表明后者可以较低的能量实现高效点火.单缸汽油机的实验表明，与传统火花塞相比，纳秒脉冲放电的点火延迟缩短3～4 倍，燃烧持续期缩短13%～17%[24].纳秒脉冲非平衡等离子体还可以减少敲缸现象[25]，具有实现稀燃发动机稳定燃烧的潜力.

除了零维计算，基于漂移扩散模型的二维模拟表明非平衡等离子体的助燃效果受压力、初始温度[13]和放电电压[26]的影响.目前大多数发动机内的非平衡等离子体助燃模型将助燃作用简化成部分自由基的添加[18,27]，而更详细的助燃机理对实现发动机稀燃状态下高效稳定点火至关重要，仍有待研究.本文通过耦合等离子体动力学、燃烧动力学和实际内燃机的压缩/膨胀过程，对比了相同放电能量条件下纳秒脉冲放电和火花放电的助燃效果及不同电流密度下纳秒脉冲放电等离子体对稀甲烷/空气混合物的助燃作用，分析了关键组分的生成速率和燃料的主要消耗路径，旨在研究给定条件下，纳秒脉冲放电非平衡等离子体如何拓展发动机稀燃极限及其背后的物理化学机制，对于更好地实现稀燃发动机的稳定点火、控制点火时间具有一定的理论指导意义.

1 模型与计算方法

本文首先建立了CH4/空气的等离子体助燃机理，包含了Defilippo 等[28]的空气等离子体模型和O3的相关反应；考虑了激发(E＋A→E＋A*)、电离(E＋A→E＋A+)、激发态驰豫(A*＋BC→A＋B＋C，A*＋BC→A＋BC 等)、离解(E＋AB→E＋A＋B)、电子-离子再附(E＋A+→E＋A)、电荷交换(A+＋B→A＋B+)等反应，甲烷的氧化反应基于GRI Mech 3.0.电子碰撞反应的速率常数基于电子与不同组分的碰撞截面，利用BOLSIG+[29]求解Boltzmann 方程得到，其中O2和N2的碰撞截面取自LXcat 的Phelps[30]和SIGLO[31]数据库，CH4的电子激发态导致离解，因此忽略其电子激发态，CH4的离解碰撞截面根据文献[32]计算.放电过程中忽略电子与产物的碰撞、电子与电子的碰撞[29].最终得到的等离子体助燃CH4/空气的详细化学反应动力学机理包含两部分：等离子动力学机理和燃烧动力学机理，共计103 个组分和1 907 个反应，其中电子碰撞反应64 个，机理中所包含的组分如表1 所示，O2(A3)是的集合.

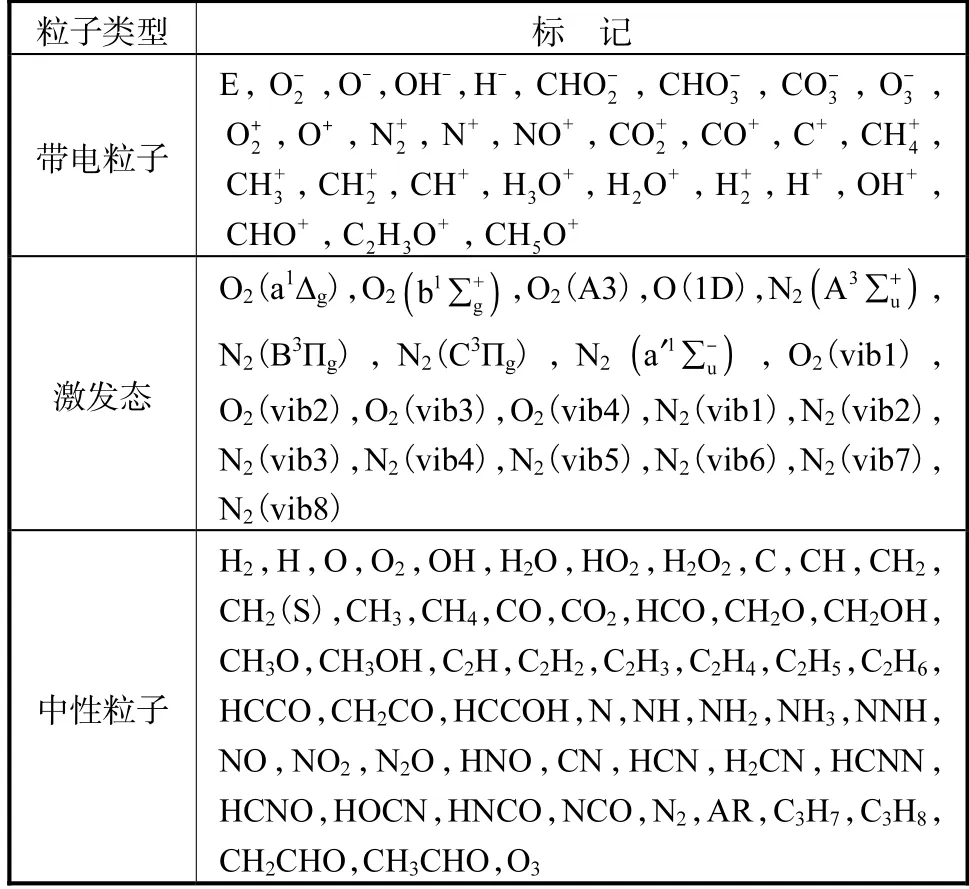
表1 详细机理中包含的组分Tab.1 Particles included in detailed kinetic mechanism

在等离子体动力学中[33]，只考虑焦耳热引起的温度变化，压缩/膨胀引起的温度和压力变化包含在燃烧动力学中.放电过程求解方程如下：

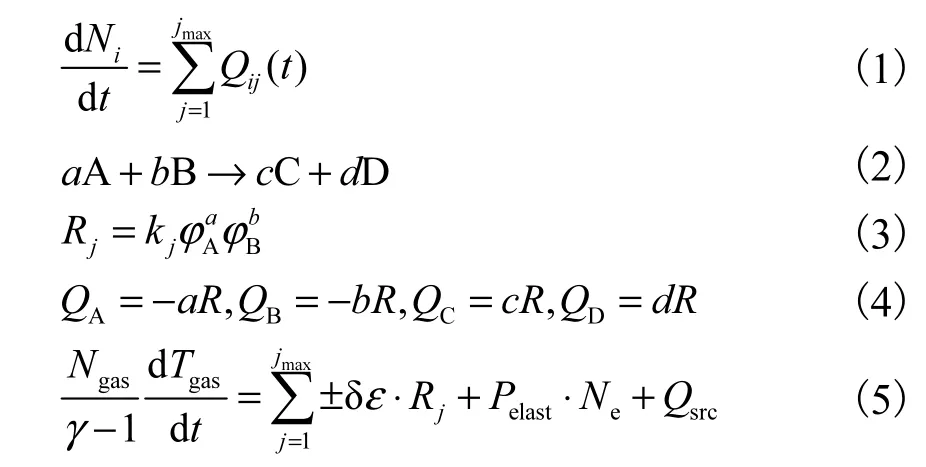
式中：Ni为组分i 的数密度；Qij为第j 个反应中组分i的生成速率；kj是反应j 的速率常数；Rj是反应j 的进程速率；δε 是化学反应放热.

在氧化阶段，将反应系统简化为一个封闭的零维系统，压缩/膨胀引起的密度变化简化为源项Sρ[34]加入组分方程.Sρ是气缸体积变化的函数，与曲轴转角、行程、转速、压缩比、缸径等发动机参数相关，具体形式见文献[34].活塞运动引起的组分k 的密度变化为SρYk，其质量分数随时间的变化率为

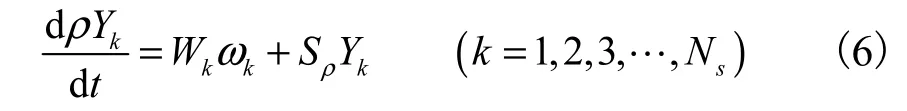
混合气的能量方程为：

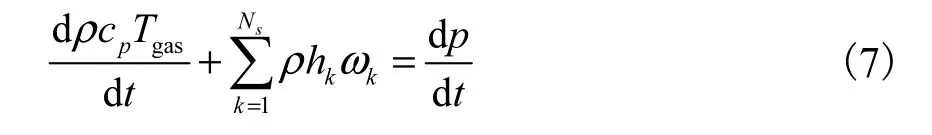
式中：ωk和hk分别表示组分k 的净生成速率和比焓，dp/dt 为压力变化率.联立方程(7)和理想气体状态方程可得系统温度、压力随时间的变化.氧化阶段存在Ns＋2 个常微分方程，均由Chemkin-Ⅲ[35]求解.

大多数纳秒脉冲放电等离子体助燃的零维模拟[8,36-37]，将等离子体动力学和燃烧反应动力学解耦，脉宽内只求解方程(1)～(5)计算等离子体动力学.主要原因为：①等离子体动力学和燃烧反应动力学的构建机理通常是两种格式的动力学参数，且涉及不同的时间尺度；②放电时间短、脉冲次数少、放电温度低，可忽略脉宽内的化学反应速率[37].与之相比，本文模拟的内燃机条件下，初始放电温度相对较高且脉冲数多(接近700 个脉冲)，忽略脉宽内的化学反应过程会造成一定误差，因此在脉宽内耦合求解了等离子体动力学和燃烧反应动力学，即求解方程(1)～(7)及状态方程.如图1 所示，每个放电脉冲内，通过ZDPlasKin 进行等离子体动力学的计算，得到的组分浓度、温度等参数继续通过Chemkin VODE求解器进行燃烧反应动力学的计算，再将计算相同时间步长后的结果输入等离子体动力学求解器，反复推进直至放电结束.脉冲间隔内约化场强为0 Td，因此只进行燃烧动力学的计算.

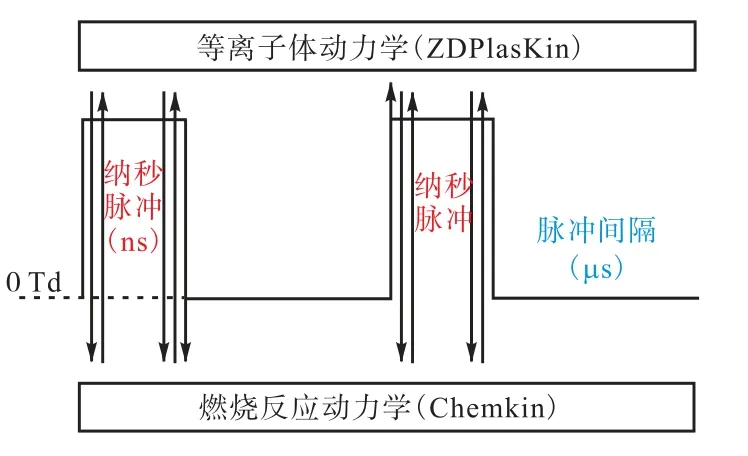
图1 纳秒脉冲等离子体动力学耦合燃烧动力学示意Fig.1 Sketch of the coupled plasma dynamics and combustion dynamics for nanosecond pulsed discharge

2 实验验证与模型对比

图2 首先对比了本文模型与实验[8]在空气及CH4/空气两个不同边界条件下单脉冲放电后O 原子摩尔分数随时间的变化.与文献[8]一致，纳秒脉冲简化为脉宽为25 ns 的方形波.如图所示，本模型较好地预测了O 原子的摩尔分数变化，特别是放电后的峰值以及氧原子的衰减过程，与实验结果吻合较好，验证了放电模型和助燃机理的有效性.

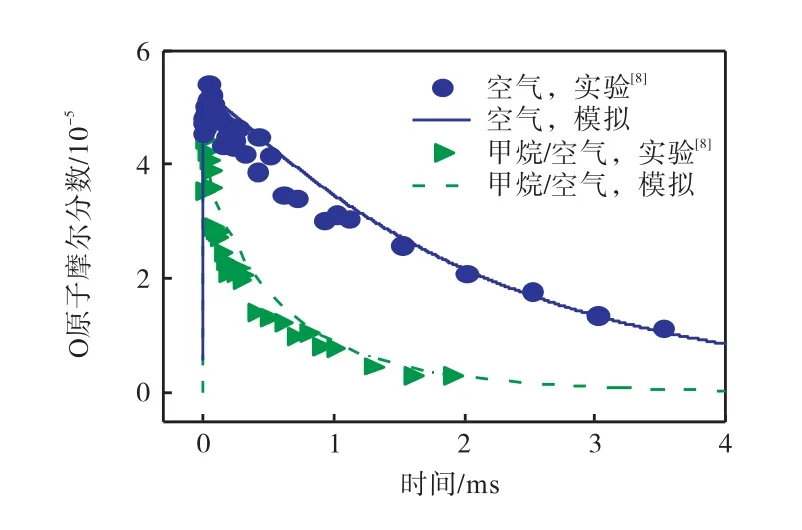
图2 O原子摩尔分数随时间的变化Fig.2 Temporal evolution of O atom mole fraction

根据文献[34]理论，首先在Chemkin-Ⅲ开源代码中建立了零维发动机模型，并与Chemkin-Pro 发动机模型进行了对比，如图3 所示.其中，发动机参数如表 2 所示[38]，进气温度和压力分别为 300 K 和0.1 MPa，进气为当量比0.5 的CH4/空气混合气.p-Chemkin-Ⅲ和T-Chemkin-Ⅲ表示本文发动机模型计算得到的压力和温度.可以看出，本模型的计算结果完全与Chemkin-Pro 重合，表明该模型可准确预测发动机压缩/膨胀引起的缸内压力和温度变化.

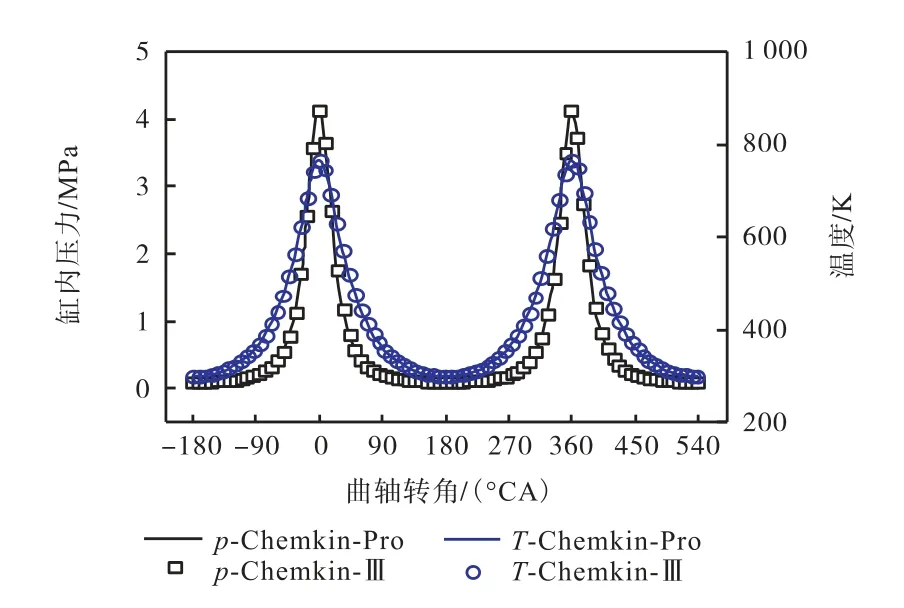
图3 纯压缩条件下本模型与Chemkin-Pro 发动机模块的缸内压力和温度的对比Fig.3 Cylinder pressure and temperature traces in a motor run(pure compression)case from current model and Chemkin-Pro with same engine parameters

表2 发动机参数Tab.2 Engine parameters

3 结果与讨论

3.1 电子能量分布函数和能量损失分数

电子能量分布函数(EEDF)表示各能级电子所占电子总数的比例，图4 所示为根据玻尔兹曼方程求解器BOLSIG+[29]求得不同约化场强(电场强度与气体数量密度之比，E/N)下，化学当量比为0.5 的CH4/空气等离子体中的电子能量分布函数，横坐标为电子能量，纵坐标表示概率密度.从图4 可以看出，随E/N的增加，能量分布函数右移，高能电子的概率密度增加，低能电子所占比例减小，因此平均电子能量逐渐增加.电子温度定义为2/3 倍的平均电子能量[29]，因此电子温度也随E/N 的增加而升高，更高的电子温度将改变能量沉积方向，导致更多的电离、离解反应发生.

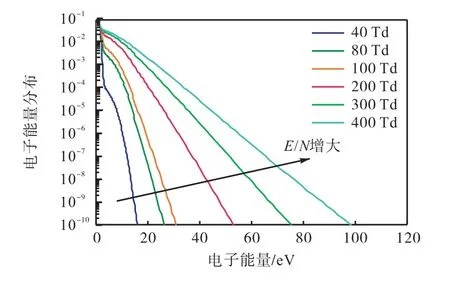
图4 不同约化场强下的电子能量分布Fig.4 Electron energy distribution function as functions of reduced electric fields for CH4/air plasma

图5 所示为相同条件下CH4/空气等离子体各碰撞反应的电子能量损失分数随约化场强的变化.可以发现，低约化场强下(E/N＜100 Td)，大部分能量用于激发氮气振动态N2(vib)；在E/N＜6 Td 时，大部分能量用于激发CH4和O2的振动态.随E/N 增大，沉积到振动激发态的能量分数逐渐减小，用于激发N2、O2电子激发态的能量分数增加，E/N 继续增加，高能电子的增加允许电子离解、电离中性组分.根据文献[39]，本文取约化场强为100 Td，大约50%的沉积能量用于激发N2的振动态.因此与文献[13,39]不同，本文的化学反应机理特别考虑了8 种氮气分子振动态及其371 个相关反应.

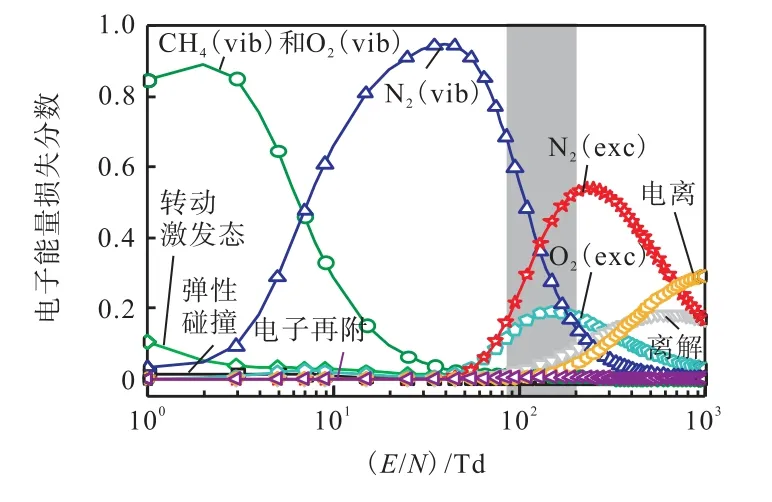
图5 CH4/空气等离子体中电子能量损失分数Fig.5 Electron energy loss fractions as a function of reduced electric fields in CH4/air plasma

3.2 等离子体助燃的动力学效应

发动机运行参数如第2 节所示，纳秒脉冲的放电频率为1 MHz，放电时刻为上止点前10°CA，持续5°CA[39].脉宽为25 ns，脉宽内约化场强为100 Td，脉间内约化场强为零[39].本文研究了稀燃发动机中不同电流密度对纳秒脉冲等离子体助燃的影响，初始电子数密度和电流密度如表3 所示.电流密度根据公式(8)计算：

表3 不同算例的参数Tab.3 Parameters of simulation cases

式中：e 为元电荷；ne为电子数密度；vdr为电子漂移速度，通过EEDF[33]计算.

首先进行了关于算例2 的时间步长的无关性分析，时间步长Δt 分别为10-9s 和10-10s，压力和温度随曲轴转角的变化如图6 所示.结果表明两者完全重合，但是前者在Intel Xeon E5-2680 处理器上计算花费约8 核时，后者是前者的8 倍，因此后续计算设置时间步长为10-9s.通常，多维等离子动力学计算的时间步长为10-13～10-12s 的量级，而大部分化学反应动力学发生在毫秒量级，巨大的差异会增加系统刚性，如何处理快反应和慢反应也是一个重要的问题[11-12].本文的零维模型忽略流场、空间电荷的影响，且ZDPlasKin 和Chemkin 分别通过刚性隐式ODE 求解器DASAC、VODE 求解动力学方程，这些求解器具有自适应时间步长的特点，可以对等离子体动力学和燃烧反应动力学的详细反应过程进行准确求解[16]，因此可以采用较大的时间步长.

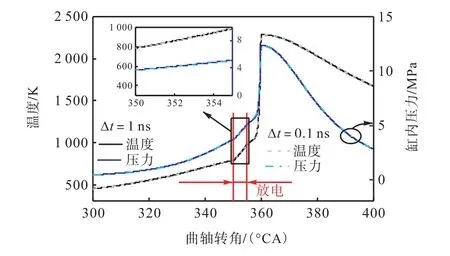
图6 不同时间步长下缸内压力和温度随曲轴转角的变化Fig.6 Temperature and pressure as a function of crank angle for different time intervals

为了对比相同能量密度条件下纳秒脉冲非平衡等离子体助燃与火花放电平衡等离子体助燃对缸内温度、压力的影响，将火花放电简化为高温恒定源项加入温度方程(7)，放电时刻与算例2 相同，持续时间也为5°CA，其中纳秒脉冲放电的功率密度根据公式(9)计算：

图7 所示为纳秒脉冲放电(算例2)、火花放电和纯压缩条件下的压力温度曲线.可以看出，电流密度为0.302 A/cm2时，纳秒脉冲放电可成功点火且燃烧相位接近上止点.但在相同能量密度条件下，火花放电产生的高温无法点燃混合气.另外，火花放电条件下，上止点处温度最高，比纯压缩条件下的最高温度高约124 K.该结果说明，若将纳秒脉冲放电的能量全部用于加热混合气，只会引起124 K 的温升，但无法实现点火.

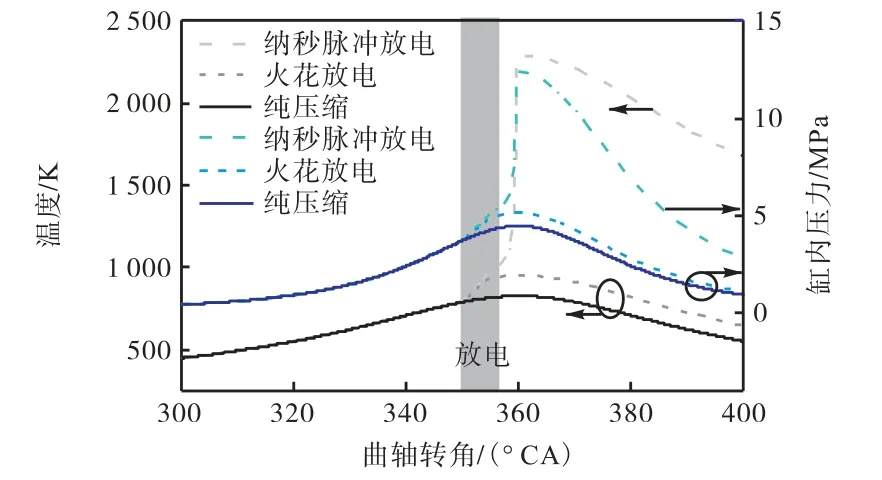
图7 纯压缩、纳秒脉冲放电和火花放电条件下，缸内压力、温度随曲轴转角的变化Fig.7 The comparison of cylinder pressure and temperature profiles among motor run，nanosecond pulsed discharge and spark discharge conditions

图8 为不同电流密度条件下温度和总释热率(total heat release rate，THRR)、压力和压力升高率随时间的变化，点火延迟定义为从开始放电到达到最大释热率的时间间隔.图中显示算例1～3 对应的点火时刻分别为：358.3°CA、359.7°CA 和373.8°CA，即随电流密度增加，点火延迟时间缩短，放电过程总释热率增加，最高温度增加.特别是算例1(高电流密度)相比于算例3(低电流密度)，最高温度增加约200 K.算例3 点火相位推迟到膨胀冲程，总释热率峰值大大降低，最大爆发压力也相应降低，不利于热效率的提高.如图 8(b)所示，当电流密度从0.378 A/cm2降低到0.302 A/cm2时，压力峰值降低，但最大压升率增加，且接近上止点.继续降低电流密度到0.227 A/cm2，压力曲线在上止点附近缓慢上升，且峰值压力大幅下降，压升率出现两个峰值，缸内出现不完全燃烧.

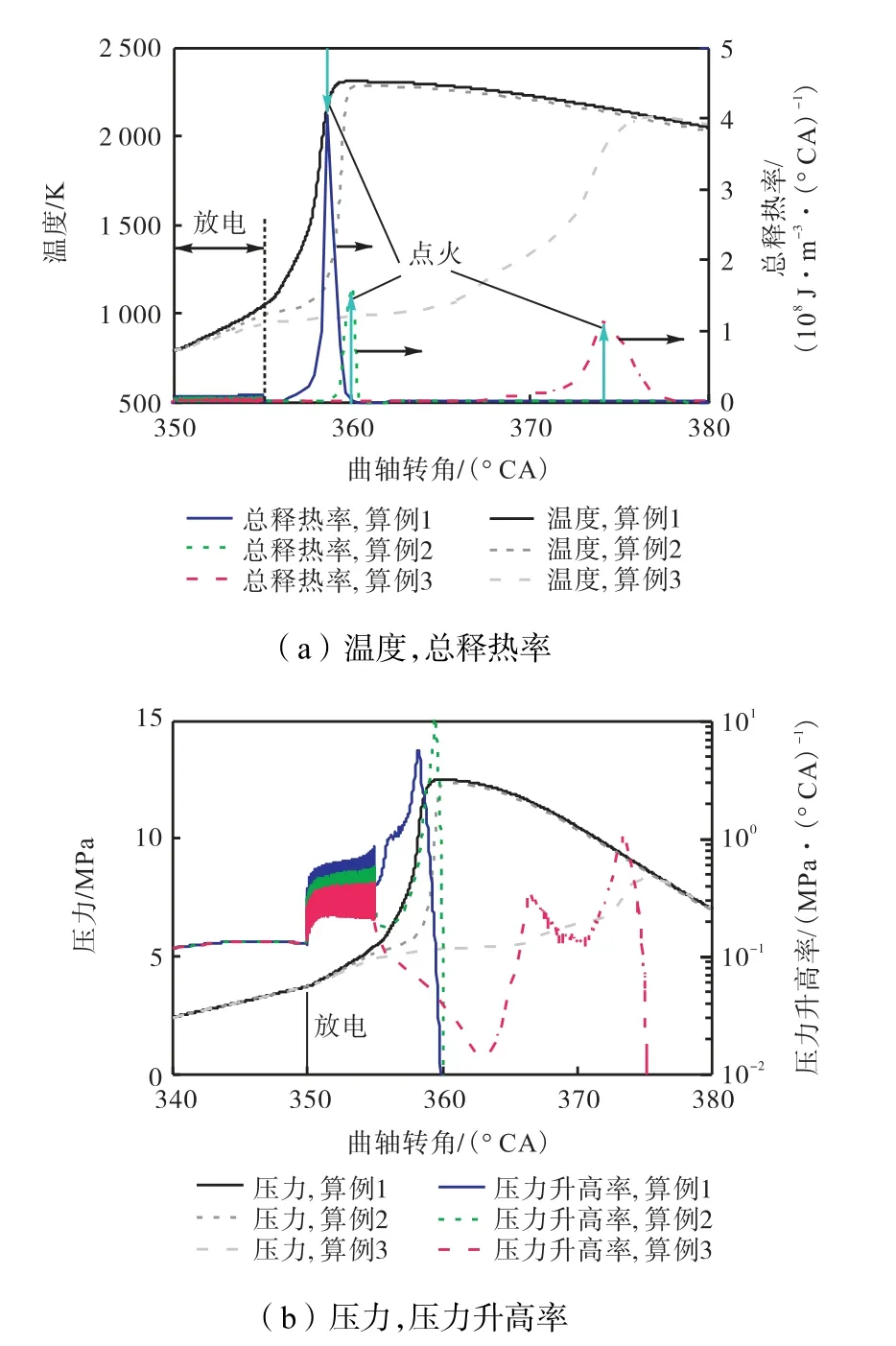
图8 不同电流密度下温度和总释热率、压力和压力升高率随曲轴转角的变化Fig.8 Temperature，heat release rate and pressure，pressure rising rate as a function of crank angle for cases 1—3

图9(a)为算例1～3 中部分活性组分摩尔分数随曲轴转角的变化.图9(b)为图9(a)在前5 个脉冲内的放大图.通常，低温条件下气体分子间的碰撞概率降低，链的激发难以实现；高活性的H、O 原子生成较少且容易重新结合形成稳定的化合物.纳秒脉冲放电提供了CH4低温氧化的可能.图9(b)显示从放电开始到放电结束(350～355°CA)，O、H、OH 活性基团的摩尔分数随时间呈周期性变化(放电开始时刻设为零时刻)，放热率呈周期性增加趋势，导致温度不断升高.而且，对比3 个算例发现高电流密度会产生高浓度的自由基.因此，图9(a)显示放电结束后，算例1 累积的自由基(O、OH、H)最多，温度最高且最先达到峰值.放电结束后算例1～3 的温度分别为1 043.5 K，988.1 K 和943.3 K.其中，算例3 电流密度过小，导致自由基浓度和温度大大减小，放电结束后的化学反应明显较慢，大量对化学释热起主要作用的中间组分O、OH 等经历了缓慢的生成阶段，直到约375°CA 时达到峰值，随后放出部分热量.

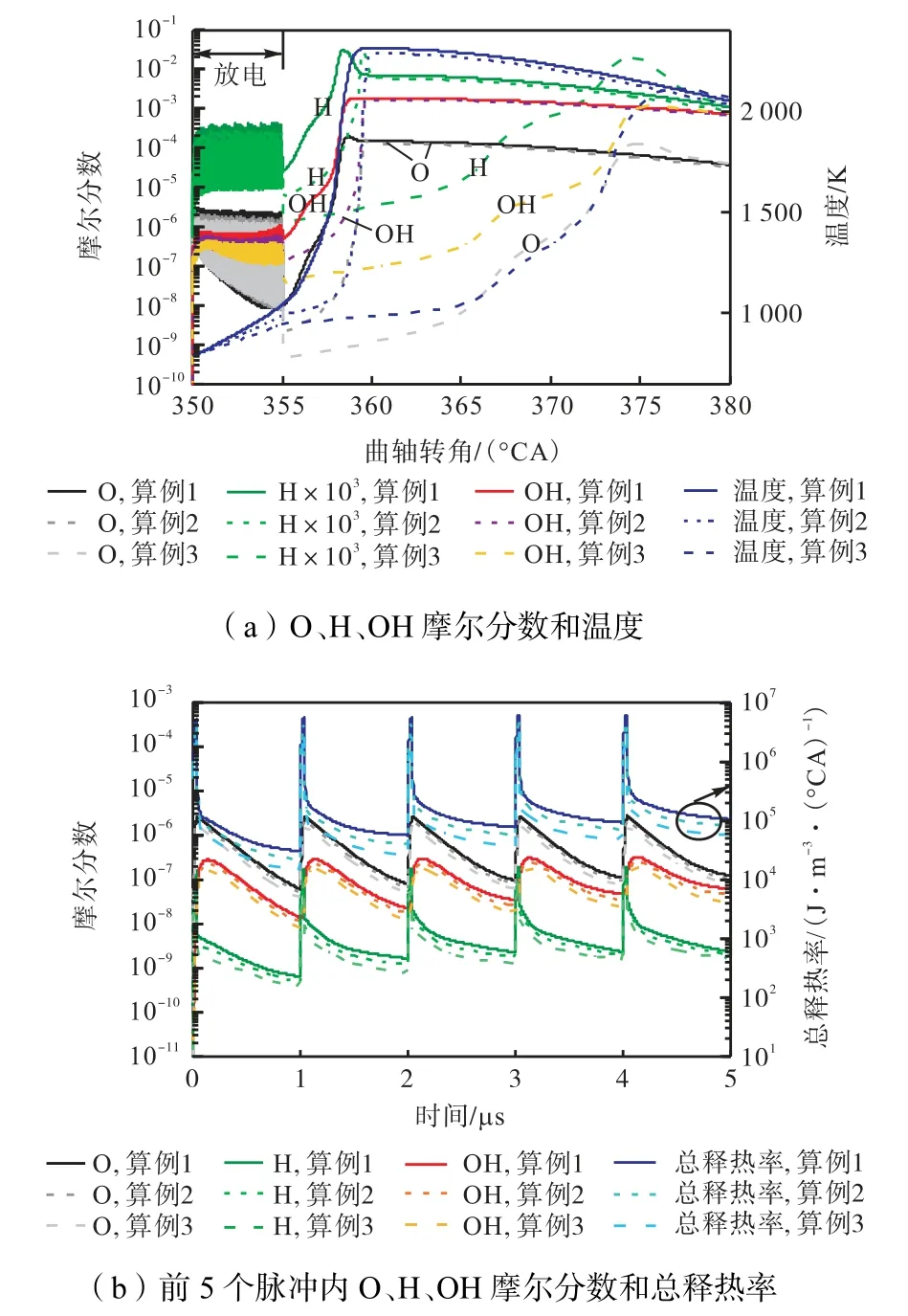
图9 算例1～3中不同电流密度下O、H、OH摩尔分数、温度和总释热率随曲轴转角/时间的变化Fig.9 The evolution of O，H and OH mole fractions，temperature and HRR with crank angle or time for cases 1—3

为了进一步揭示等离子体动力学对组分生成的影响，图10 显示了第1 个放电脉冲期间算例1、3 中O、H 原子主要生成路径的反应速率.由图10(a)可以看出，对氧原子生成贡献最大的两个反应是的驰豫反应(R421)和(R475)，说明N2含量较多的稀混合气中更容易生成大量氧原子[19].第3个重要反应是激发态 O(1D)与氮气的反应，而O(1D)的生成也与有关.第4 个反应是电子直接碰撞氧气分子离解为O 原子，该反应对其生成贡献率较低.随电流密度增加，这4 个反应的反应速率均增大，因此高电流密度导致放电过程生成了较多的O 原子.类似地，低温下H 原子的生成较为困难，但图10(b)显示电子和分别通过反应(R1817)、(R401)离解CH4，因此第1 个放电脉冲结束时，电子和N2激发态对甲烷的离解有效地促进了H 原子的生成.另外，所有反应都表现出相同的趋势，即电流密度越大，H 原子生成速率越大.总体而言，算例1 在放电结束后可以生成更多的H 原子.

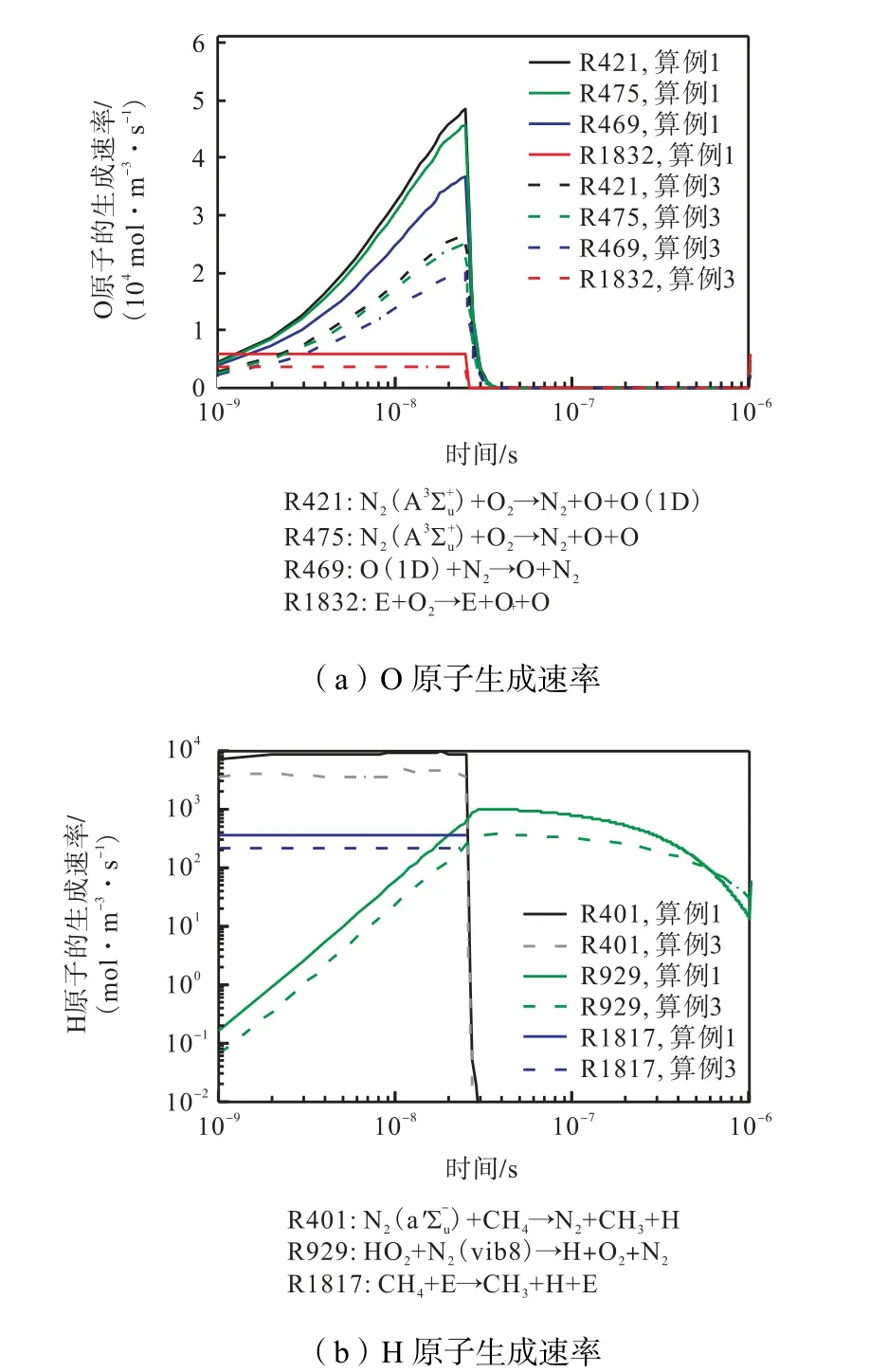
图10 第1 个脉冲内算例1 和3 中O 原子和H 原子的生成速率随时间的变化Fig.10 The production rates of O atom and H atom as a function of time for case 1 and case 3 in the first pulse

除了分析自由基的生成路径，图11(a)还对比了第1、10、30 个放电脉冲中主要反应的放热率.可以看出第1 个脉冲内，高电流密度导致电子的再附反应O2＋E＋O2→＋O2(R1412)释放出较多的热量，高于非等离子体反应的放热量.第1 个放电脉冲结束，混合气温度略有增加.随放电的进行，小组分浓度不断 累 积，反 应 H ＋O2＋N2→HO2＋N2(R36)和2CH3(＋M)→C2H6(＋M)(R158)的释热率逐渐增加.而且电流密度越大，自由基浓度越大，相关反应的释热率越大.第30 个放电脉冲结束后，算例1 的温度比算例3 高2 K.

图11(b)所示为放电结束(355°CA)后部分反应的放热率，曲线的截断表明某些组分消耗殆尽，该反应不再发生.图中显示算例1 在356°CA 之前，氮气、氧气激发态参与的反应(R1397)和(R352)的释热率比化学反应(R99)：OH＋CO=H＋CO2的大.这是由于 N2(vib1)和 O2(vib1)分别具有 0.29 eV 和0.196 eV 的激发能量，N2(vib1)通过反应(R1397)在驰豫过程中释放出0.094 eV 的能量，而此时缸内温度和活性组分不足以促使主要的氧化反应放热.但随活塞上行，缸内温度和压力继续升高，356°CA 后反应(R99)的放热开始占据主要地位.一般来说，对于碳氢燃料的燃烧过程，反应(R99)标志着链的终止，同时也是高温区最主要的放热反应之一.图11(b)也显示，随电流密度减小，反应(R99)、(R352)和(R1397)的放热率峰值时刻推迟，燃烧相位滞后.综上所述，等离子体的存在添加了新的放热反应路径，有助于提高混合气温度.

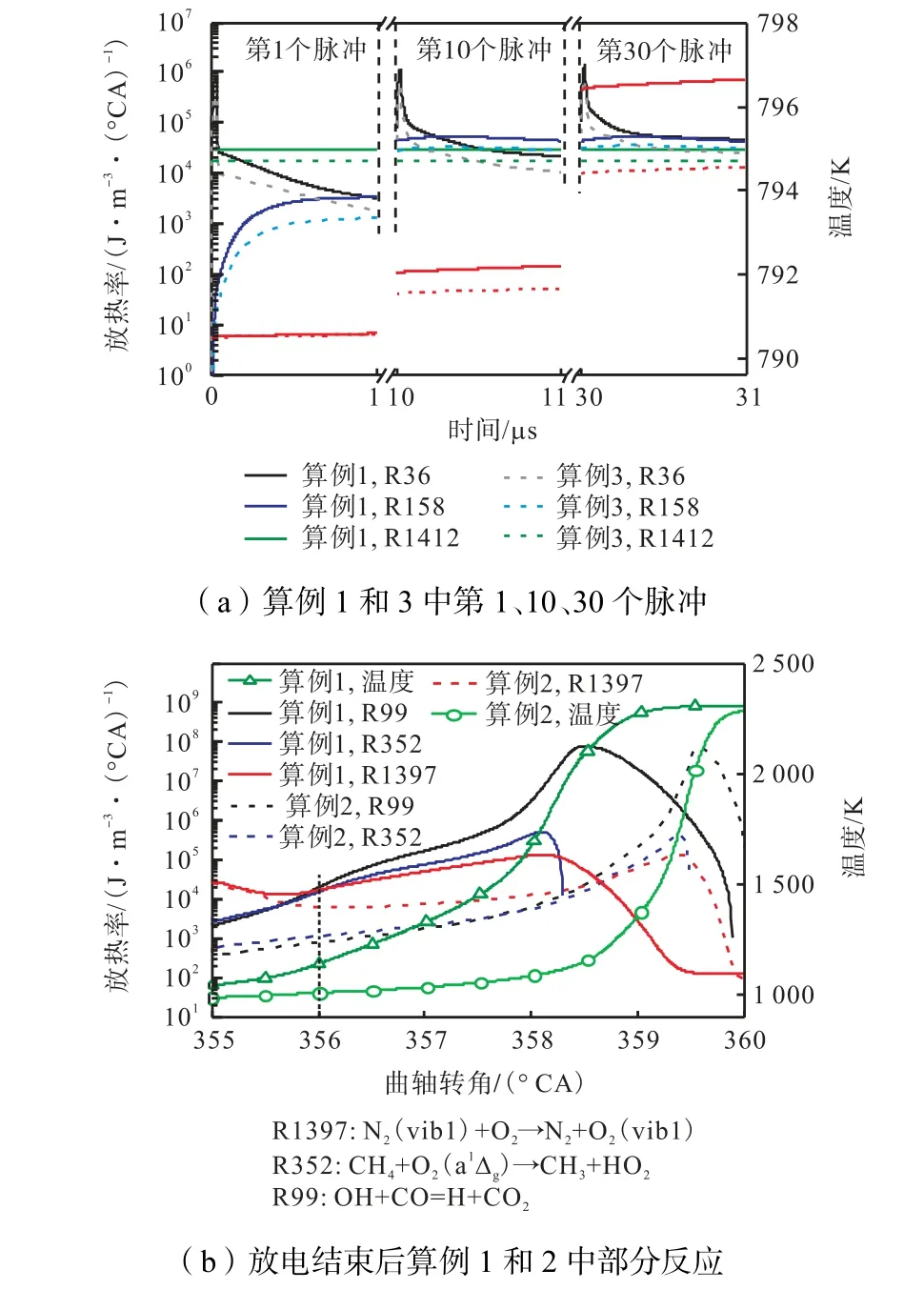
图11 部分反应的放热率和温度随时间/曲轴转角的变化Fig.11 The variation of temperature and HRR of partial reactions with time/crank angle

以上研究说明非平衡等离子体放电不仅会产生激发态、自由基等活性组分，也会增加、改变燃料的消耗路径.图12(a)和(b)分别是放电结束后算例2中CH4的主要消耗路径和O 原子的主要生成路径，且量化了各主要反应的贡献率[8].通过路径通量分析可以看出，OH 和O 是消耗CH4的主要组分，N2激发态消耗了5.17%的CH4，而电子对CH4消耗的直接影响仅占 0.31% .图 12(b)指出 N2激发态与氧气的反应对O 原子的生成贡献率为58.45%，是最主要的O 原子生成路径.其次，单态氧O(1D)与氮气的反应贡献了30.69%的O 原子，大约4.77%的O 原子来自电子和氧分子的直接碰撞，与图10(a)结论类似，这说明在发动机稀燃条件下，纳秒脉冲放电产生的N2激发态和单态氧原子极大地促进了O 原子生成.

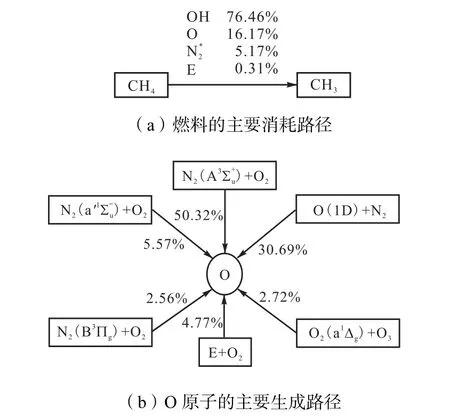
图12 放电结束后燃料的主要消耗路径和O 原子的主要生成路径Fig.12 The main consumption path of fuel and path flux integrated over time for O atom at the end of discharging

4 结论

本文通过耦合等离子体动力学和燃烧反应动力学，在发动机条件下计算了纳秒脉冲放电非平衡等离子体对稀CH4/空气(φ=0.5)的助燃过程；对比了相同能量密度条件下纳秒脉冲放电和火花放电对稀混合气的助燃效果；研究了纳秒脉冲放电条件下，不同电流密度导致的活性组分、温度和燃烧相位随发动机曲轴转角的变化.得出以下结论：

(1) 随约化场强增大，平均电子能量增加.在稀混合气、低约化场强条件下，大部分放电能量沉积于N2的振动激发态和电子激发态.

(2) 给定相同的能量，纳秒脉冲放电可以在上止点附近成功点燃稀混合气，但火花放电只能使最高温度升高约124 K，无法成功点火.

(3) 在纳秒脉冲放电过程中，O 原子的生成与等离子体密切相关.在驰豫过程中离解O2，为CH4的低温氧化提供了大量氧原子，单态氧原子O(1D)的存在也促进了O 原子的生成，且低温下促使CH4离解生成H 原子和CH3，引发了链式反应.放电初期电子再附反应的释热对温度贡献较大，放电后期累积的N2振动激发态在驰豫过程释放出了较多的热量，在电子、自由基和激发态的共同作用下，混合气温度升高，有利于稀燃条件下的点火.

(4) 随着电流密度增加，纳秒脉冲放电过程产生了更多的激发态如、O(1D)等，进而生成了较多的自由基如H、O、OH，促进了链式反应的进行，导致放电结束后较高的自由基浓度和温度，缩短了点火延迟时间.