基于标量衍射理论的两种等大倒立实像系统研究

熊学辉，杨书羽，朱春莲

（1.江汉大学光电材料与技术学院，湖北 武汉 430056；2.武汉墨光科技有限公司，湖北 武汉 430074）

0 引言

透镜本质是一种可实现空间相位变换的元件，不仅具有成像功能，还具有空间傅里叶变换功能［1-2］。透镜的傅里叶变换性质使得傅里叶分析方法在光学信息处理中得到广泛应用。而4f系统可以实现物体准确的傅里叶频谱，通过在该系统中的频谱面上进行有目的的处理可改变物体的像，基本的4f系统进行一些特定的改进可被广泛应用于光学检测和光学图像处理等领域［3-6］。韩亮课题组［3］为将光学小波变换应用于图像压缩，分析了光学4f系统中图像实现方式和图像采集对图像空间频率特性的影响。其研究结果表明，利用光学4f系统实现光学小波变换理论，可以极大地减少小波变换所花的时间，具有理论和实用价值。文献［4］指出，利用4f系统的阶跃响应对峰峰信噪比和结构相似度指数都有很好的复原效果，其分别提高了5 dB和6%左右。快捷可靠的测量技术一直是非线性光学研究领域的热点之一，文献［5］综述了利用4f相位相干成像技术分析测量材料光学非线性系数的原理、方法等。王悦等［6］研究了紧凑型矢量光场发生器中4f系统在横向和纵向上的精确对齐方法，通过相位图对系统中的透射式4f系统和反射式4f系统进行纵向对齐，以确保生成光场的清晰程度，减小了光场的衍射反应，对于其他含4f系统的光路有借鉴意义。4f系统也一直应用于激光散斑干涉系统研究［7-9］中。笔者在基于4f系统的散斑干涉法实现图像相减实验中，发现利用4f系统制备的二次曝光散斑全息图能得到散斑干涉的条纹图，从而实现后面的滤波和图像相减；而利用元件个数少、光路简单的单透镜4f成像系统实现的二次曝光全息散斑图却不能得到干涉条纹。基于该实验，笔者对这两个都能成等大倒立实像系统的成像差别进行了研究，利用标量衍射理论详细计算推导了这两种成像系统像面光场的分布。

1 两种成像系统比较

光学信息处理系统中，广泛使用的标准4f系统可以得到物体准确的傅里叶频谱，经过两个傅里叶变换透镜，在第二个傅里叶变换透镜的像方焦平面上得到物体等大倒立的实像。而当物体放在单透镜的2倍物方焦距处时也能在2倍像方焦距平面上成等大倒立的实像。标准4f系统（见图1（a））由两个大口径傅里叶变换透镜L1和L2组成，物平面（x0，y0）放在第一个傅里叶变换透镜L1的物方焦平面，此时物平面到透镜L1的距离为f，即第一个f距离。物方光场经傅里叶透镜L1后，L1的像方焦平面也就是物方光场的频谱面（x′，y′），透镜L1到物方频谱面的距离也为f，即第二个f距离。该频谱面距离傅里叶透镜L2也恰好为焦距距离，为第三个f距离，物方频谱经过第二个透镜L2的傅里叶变换，在其焦平面处得到物体的像平面，为第四个f距离。因此，物面和像面的距离为4f。图1（b）为只含有1个成像透镜L的4f系统，当物平面（x0，y0）放在透镜的二倍物方焦距处时，成像在二倍像方焦距平面（x，y）处，物平面和像平面间的距离也是4f。

在图1中标注了各面的特性和坐标符号，也利用几何光学作图法画出了两种系统光路示意图。对于探测光强的成像光学系统，这两种系统所成像的性质一样，都成等大倒立的实像。但是对于信息光学系统，特别是相干光学系统，需要使用系统的像面光场复振幅分布特性进行分析。本文将从波动光学出发，利用标量衍射理论计算推导两种系统的像面光场分布。

图1 两种等大倒立实像系统光路图Fig.1 Optical path diagrams of two equal size inverted real image systems

2 单透镜4f成像系统像面光场复振幅推导

首先根据标量衍射理论，利用光线在相距有限距离远的面间传播时的菲涅耳衍射模型，推导图1（b）所示的单透镜4f成像系统物像光场关系。设单位平行光垂直照射到物平面，光波从物平面传播到透镜前表面，两面间隔两倍焦距距离d=2f，可以用菲涅耳衍射模型；由于透镜元件的相位转换性质，透镜后表面的光场与透镜前表面的光场并不相同；透镜后表面到像平面距离也是2f，光波的传播满足菲涅耳衍射模型。

具体推导如下：

第一区间从物面（x0，y0）到透镜前表面（xl，yl），发生菲涅耳衍射，z=2f，代入菲涅耳衍射公式，可求得透镜前表面的光场复振幅分布

式中，k表示波数；λ表示波长；U0(x0,y0)表示物平面光场。

第二区间从透镜前表面到透镜后表面，利用理想透镜的二次相位变换作用得到透镜后表面光场

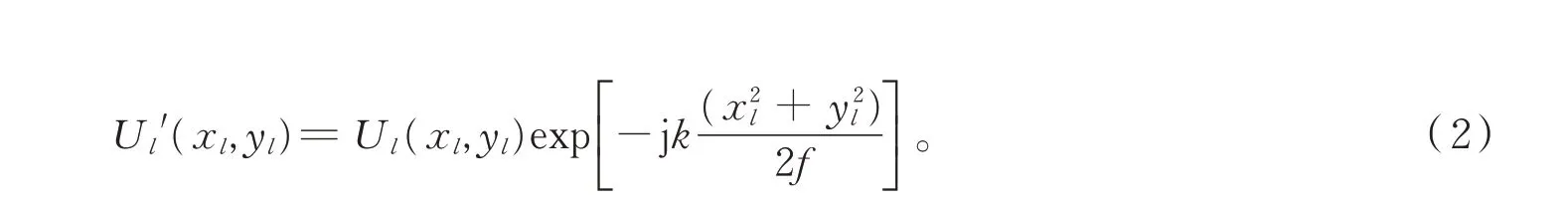
将（1）式求得的透镜前表面光场Ul(xl,yl)代入（2）式，得透镜后表面光场

第三区间从透镜后表面（xl，yl）到像平面（x，y）也是菲涅耳衍射，于是像面光场

将（3）式代入（4）式得

（5）式体现了物平面光场分布与像面光场的关系，经历了四重积分，对（5）式展开，并对两个平面上的积分变量（xl，yl）和（x0，y0）分别进行合并同类项，不参与积分的项提出积分外，

化简式（6）得

将式（7）中

凑成

该项的积分项是常数1的傅里叶变换，得到脉冲函数(2fλ)×(2fλ)δ(x0+x,y0+y)，将该积分结果应用到（7）式，得

对于（8）式，还需对物平面上（x0，y0）进行积分，其中被积函数二次项对像面光场有影响的必定只是物面上以几何成像所对应的物点为中心的微小区域［1-2］。设物面像面放大率为M，则在这个微小区域（x0，y0）可近似为x0=x/M，y0=y/M，在本例中，放大倍数为M=-1，代入得

这样该被积项近似与积分变量无关，可以提到积分外，（8）式继续化简为

对于（9）式积分项，利用δ函数的筛选性质得到

则（9）式最终可化简得到像面光场复振幅分布关系式

由（10）式可知，当物体放在两倍焦距时，像面光场复振幅U(x,y)中前面的负号表示物像放大倍数为-1，成等大倒立的实像，有一个常数相位因子exp(j4kf)项，以及随像面不同坐标位置（x，y）变化的相位因子，像方光场含有U0(-x,-y)，说明在像面的光场与物面光场相似，只是像面的坐标系统和物面的坐标系统成镜像。

以上利用标量衍射理论中光波传播的菲涅耳衍射模型详细推导出单透镜4f系统物像光场关系（10）式，该式充分体现了像方光场与物方光场函数相似，只是多了相位因子。几何成像系统探测的是光强I=U(x,y)U*(x,y)，相位因子对光强分布没有影响。

3 标准4f系统像面光场的复振幅推导

由于标准4f系统完成两次傅里叶变换，所以本节推导可以不利用最基本的菲涅耳衍射模型，不需要逐面利用菲涅耳衍射模型和透镜的相位变换特性来推导。很多信息光学教材［1-2］都推导了当平行光束垂直照射物平面，物体放在物方焦平面时，经过单个透镜的傅里叶变换，在该透镜的像方焦平面上得到物体的准确频谱，这一基本傅里叶变换表达式如公式（11）所示。本节推导就是按标准4f系统布局的两个透镜实现两次傅里叶变换来展开。

在标准4f系统中，物体放在傅里叶透镜L1的前焦平面，设物面光场为U0(x0,y0)，则在L1的后焦平面上得到物体的准确傅里叶变换，即物体的频谱。频谱面(x′,y′)上的光场复振幅数学表达式为

表明物平面信息U0(x0,y0)经透镜L1的傅里叶变换作用得到物体的频谱信息U′(x′,y′)。而频谱U′(x′,y′)再经傅里叶透镜L2变换到像平面（x，y）又完成一次傅里叶变换，得到物体的像平面光场分布U(x,y)，即

将（11）式代入（12）式，得到四重积分，

将上述四重积分函数里被积指数函数变形为傅里叶变换的标准核形式

先将x′,y′积分变量凑成形式，积分变为

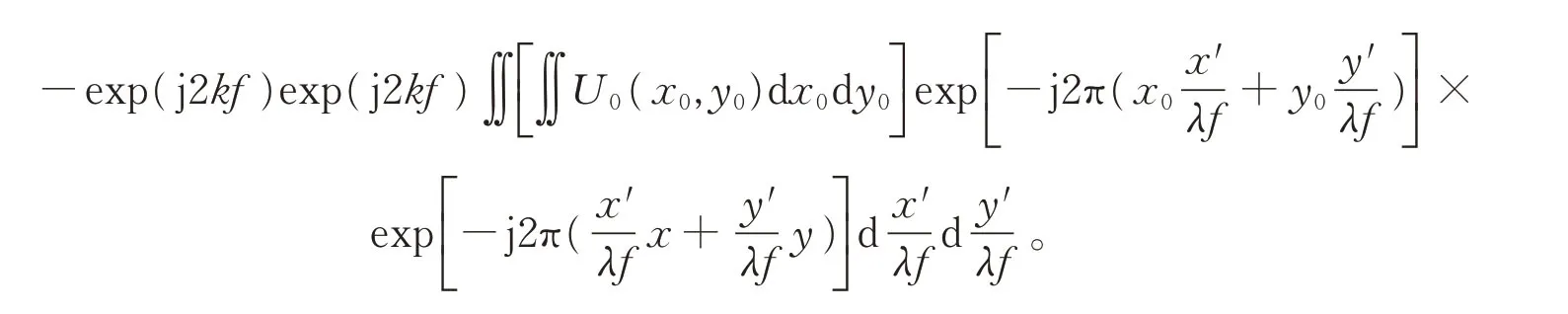
对被积函数中含有积分变量x′,y′的项进行合并同类项，得

对于x′,y′积分，上式相当于原函数为1的傅里叶变换，得到δ函数

利用δ函数的性质得

上面利用傅里叶变换式详细推导出标准4f系统像面和物面光场的关系式（13），前面的负号表示物像放大倍数为-1，即成等大倒立的像；像面的坐标系统和物面的坐标系统成镜像，物、像光场只相差一个常数相位因子exp(j4kf)。

几何成像系统探测的是光强I=U(x,y)U*(x,y)，相位因子对光强分布没有影响。

综合对比单透镜4f成像系统像面光场复振幅关系（10）式和标准4f系统像面光场复振幅关系（13）式，发现两种系统的像面分布仅仅相差一个相位因子。

4 结语

本文主要利用标量衍射理论研究了标准4f系统和单透镜4f系统像面光场复振幅分布。结果表明，两种系统的像面光场都含有因子-exp(j4kf)U0(-x,-y)，但单透镜4f系统比标准4f系统多了一个随像面不同坐标位置（x，y）变化的二次相位因子。这两种成等大倒立实像系统，用人眼或探测器去检测时，探测的是光强，不受像面光场相位因子的影响，所以这两种成像没有差别。但是在更精密的相干信息光学系统中，如果要用像面光场与另一相干光干涉，那么这时候的相位因子影响就不能忽略，比如散斑干涉二次曝光全息图，利用单透镜成像系统制备的干版不能得到预期的干涉条纹。通过本文的分析，不仅有利于指导实验，还可以加深学生对光场复振幅分布和光强关系的理解，有助于学生理解干涉时相位因子的重要性。