基于模糊算法的锂离子电池组主动均衡方法

吴铁洲，李梓豪

(湖北工业大学太阳能高效利用及储能运行控制湖北省重点实验室,湖北武汉 430068)

锂离子电池因其循环寿命长、功率密度高、自放电率低等优点[1]，在许多领域引起了广泛的关注。但由于锂离子电池特性，单体锂离子电池电压较小，通常低于要求的工作电压，所以，在实际应用中需要多个单体锂电池组成电池组[2]，而锂离子电池组里存在各个单体电池的不一致性问题，在充放电过程中会发生单体电池出现过充或过放等情况，会对电池造成危害[3]，因此对电池组进行均衡是非常必要的。

现在已经有大量学者研究均衡技术与均衡方案。均衡方法有主动均衡和被动均衡[4]。被动均衡是能耗性均衡，将单体电池和电阻并联起来，多余的电能以热能的形式通过电阻释放掉，但这种方式会造成较多能量损失[5]。文献[6]中将荷电状态(SOC)作为均衡变量，对锂电池组进行被动均衡，结构简单，能够有效地降低电池的不一致性，但能量消耗也比较严重。综合考虑均衡过程中的均衡速度和能量利用率等问题，主动均衡成为了当下研究热点。

主动均衡控制变量一般为电压和荷电状态(SOC)，其中采用较多的是电池电压，但单独采用电压作为均衡变量时，会导致电路中的开关管频繁地导通和关断，电池之间的能量转移次数增加，这会造成开关管损耗和电池老化速度加快。

文献[7]提出，当SOC处于0%～20%或80%～100%时，开路电压和SOC之间的关系曲线斜率绝对值较大，极小的SOC差值误差就会导致单体电池间的电压差极大，会影响电池组均衡的准确性。对于这个问题，文献[8]中提出一种双阈值混合均衡控制策略，将整个电池组均衡周期进行分段，当SOC处于20%～80%时以SOC作为均衡变量，反之，则以电压作为均衡变量。

当电池组中单体电池数量过多的时候，电路复杂度和控制难度也是一个需要解决的主要问题。文献[9]提出了一种双层桥臂的带有附带电源的Cuk 电路拓扑，这种拓扑结构可以实现能量的双向流动，但面对电池组功率有较大要求的情况时，需要串联大量的单体电池，电路的控制难度会大幅度增加，实用性较低。为了应对电池组在实际应用中会遇到的情况，均衡电路的拓扑结构应该能够尽量降低控制难度。

针对以上电池组均衡可能会遇到的问题，本文提出了一种基于模糊算法的锂离子电池组主动均衡方法。首先，设计了一种可以在电池组中任意单体电池间进行能量传递的新型拓扑结构。其次，将整个电池组均衡周期进行了分段，分别以SOC和电压作为均衡控制变量。最后设计了以SOC和电压作为控制变量的模糊控制器，对均衡过程输出电流进行调整。

1 均衡电路分析

1.1 均衡拓扑结构

本文采用了一种基于双向DC/DC 电路的任意单元间能量转移拓扑结构。总体均衡方案如图1 所示，拓扑的主要结构为双层开关和均衡主电路。双层开关分别连接串联电池组的每个单电池的正极和负极，分别为S1-Sn和K1-Kn。均衡电路的主回路采用的是非隔离型的双向DC/DC 电路，其电路元器件包括电感L、电容C1和C2、主控开关器件Q1和Q2以及二极管D1和D2。

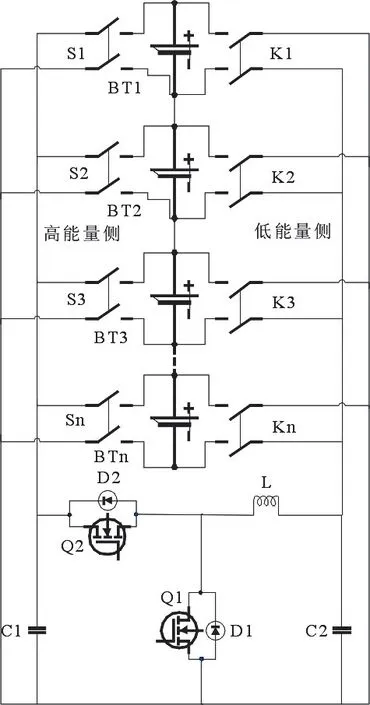
图1 基于任意单体电池间能量转移的拓扑结构

此均衡拓扑有以下两个优点：

(1)相比传统的相邻电池间能量传递的电路拓扑，此电路拓扑能够通过选择开关通断实现任意电池间的能量传递，从而缩短能量传输路径以及较少开关损耗，间接提高能量利用率，缩短均衡时长。

(2)当电池组电池数量增加时只需增加选择开关的数量，电路复杂度不变。

控制策略为采集电池组各个电池的电压和SOC值，通过模糊控制器的模糊规则输出电流调整均衡过程，再通过运算调节占空比，进而控制MOSFET。

1.2 双向DC/DC 电路能量传递

图1 规定右侧开关S 控制的是低能量侧，左侧开关K 控制的是高能量侧，即能量由高能量侧放电通过双向DC/DC 能量传递电路传递到低能量侧，给其充电，从而完成能量传递。双向DC/DC 电路见图2。本文采用非隔离型双向Buck-Boost电路作为电池组的均衡主电路。这种电路所需元器件数量较少，成本较低，无变压器损耗，均衡效率高。

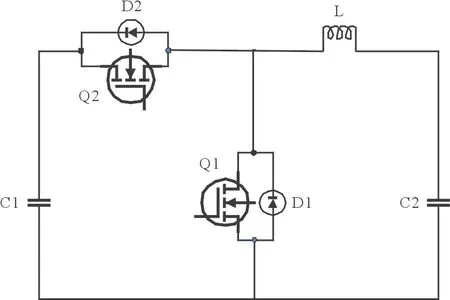
图2 双向DC/DC电路

当电池组进行充电均衡时，电路工作在Buck 模式下，开关管Q2按照信号给定的占空比进行导通和关断，Q1既可关断也可导通互补，D2为续流二极管，能量由放电端流向充电端；当电池组进行放电均衡时，电路工作在Boost 模式下，能量由充电端流向放电端。如此即可完成锂电池组在充放电均衡时的能量流动。

2 模糊逻辑控制策略设计

根据整个周期范围内的SOC变化特征，采用分片均衡的方式，在不同的SOC变化范围内选择不同的均衡控制变量，以提高均衡效率。根据文献[8]，当SOC处于0%～20%和80%～100%两个区间时，开路电压变化较大。因此，对于低SOC平均值，若将SOC作为均衡变量，当电池以大电流放电，会造成工作电压急剧下降。这种电压下降会导致内阻大的电池过度放电。同样，如果电池的平均SOC相对较高，SOC高的电池可能会被过度充电。在充放电过程中，以唯一的均衡控制变量难以准确的表征电池之间的不一致性。因此，本文将电池SOC的范围进行分段，根据电池OCV-SOC特性曲线，将电压和SOC作为均衡控制变量。当SOC处于0%～20%或80%～100%时，采用电压作为均衡控制变量；当SOC处于20%～80%时，选择荷电状态作为均衡控制变量。

2.1 均衡控制策略

本文的均衡控制策略是设计模糊控制器，利用模糊控制算法以SOC和电压作为变量，输出得到均衡电流，从而实现提高均衡效率的目标。模糊控制流程图见图3。模糊控制器由模糊器、模糊规则库、推理引擎和去模糊器组成。先通过模糊器将输入量模糊得到模糊变量，然后将模糊变量输入推理引擎，根据模糊规则进行处理，最后将处理结果通过去模糊器转化为精确的输出。

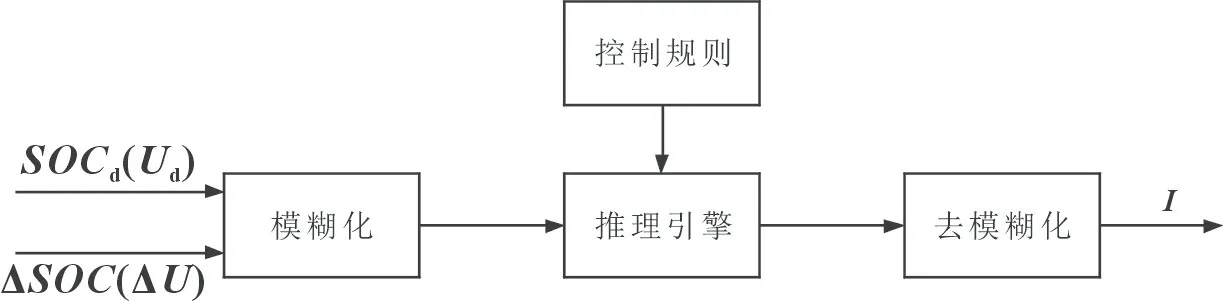
图3 模糊控制流程图

基于模糊逻辑控制的电池均衡方案流程图见图4。在本文中，分别设计基于电压和基于SOC的两种不同的模糊控制器。两个模糊控制器的隶属度函数和模糊控制规则是相似的。以基于SOC的模糊控制器为例，电池组单体电池的平均SOC值(SOCp,av)与处于均衡过程的两只电池的SOC平均值的差值(ΔSOCav)的绝对值和处于均衡过程的两只电池SOC的差值(ΔSOC)的绝对值作为模糊控制器的输入，表达式见式(1)～式(4)。

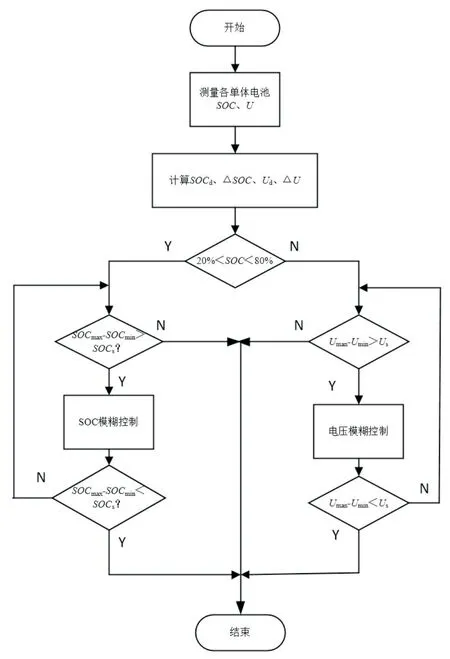
图4 基于模糊逻辑控制的电池均衡方案流程图

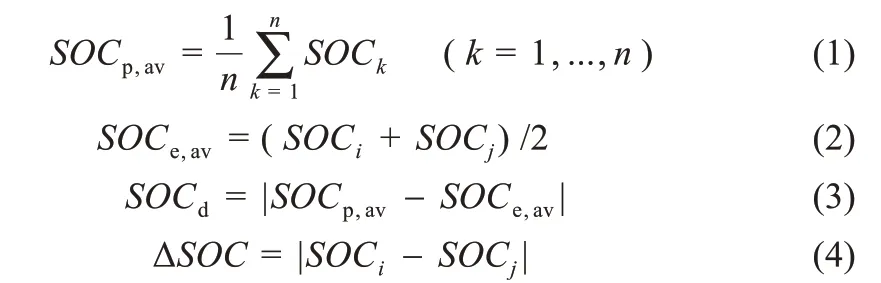
式中：SOCi和SOCj分别表示为均衡过程中充电和放电的两个单体电池的SOC值；SOCp,av是电池组平均SOC值，SOCe,av为处于均衡状态的两只电池的平均SOC值；ΔSOC为均衡两只电池的SOC差值；SOCd表示均衡电池SOC与电池组SOC的差异。

2.2 模糊逻辑控制设计

根据第2 节分析，结合专家经验对模糊控制模块进行设计。在SOC处于20%～80%的范围内时，以SOC作为控制变量进行模糊控制。

输入量SOCd和ΔSOC的隶属度区间分别设为0%～20%和0%～60%，分成极小(VS)、小(S)、中(M)、大(L)和极大(VL)五个子集。

同样的，在SOC处于0%～20%或80%～100%的范围内时以电压作为控制变量进行模糊控制，输入量Ud和ΔU的隶属度区间分别设为0～0.2 V 和0～1.2 V，同样分为极小(VS)、小(S)、中(M)、大(L)和极大(VL)五个子集。

两种模糊控制方案的输出量为I，根据电池允许的最大电流设置其范围为0～5 A，分为极小(VS)、小(S)、中(M)、大(L)和极大(VL)五个子集。图5 和图6 分别为基于SOC和基于电压隶属度函数图。

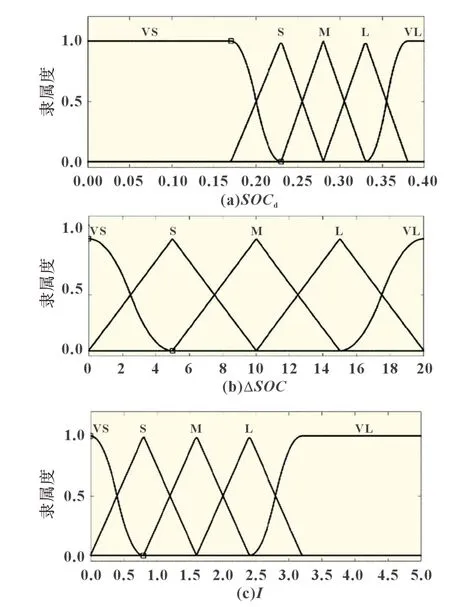
图5 基于SOC的隶属度函数图

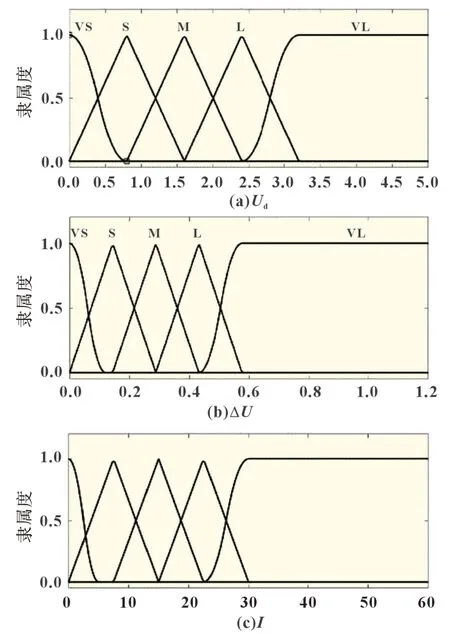
图6 基于电压的隶属度函数图

为了实现提高电池组均衡效率的目标，模糊控制需要实现以下基本要求：

当SOC处于20%～80%时，如果SOCd较大，并且ΔSOC也较大，则输出较大的均衡电流来减少均衡时间；如果ΔSOC较小，并且SOCd也较小，则输出较小的均衡电流以免对电池造成损害；同时可以根据SOCd和ΔSOC的大小输出合适的均衡电流。

当SOC处于0%～20%或80%～100%时，如果Ud较大，并且ΔU也较大，则输出较大的均衡电流提高均衡速率；如果Ud较小，并且ΔU也较小，则输出较小的均衡电流以免发生过充；同时可以根据SOCd和ΔSOC的大小输出合适的均衡电流。

基于以上要求，分别设置基于SOC和基于电压的模糊规则，两种控制变量的模糊规则见表1 和表2。

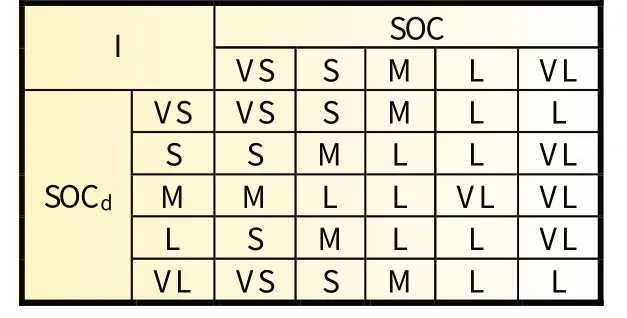
表1 基于SOC 的模糊规则

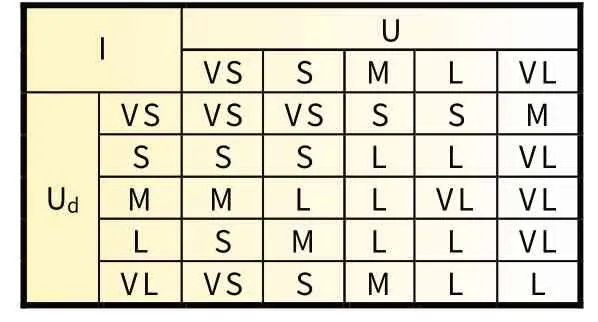
表2 基于电压的模糊规则

通过模糊控制器得到的模糊量并不是准确的电流值，应该对其进行去模糊化，得到精确的值，再用于电池组均衡。本文选择面积中心去模糊法，表达式如式(5)所示：

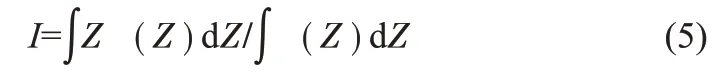
式中：j (Z)是推理的模糊结果。

然后，通过去模糊化得到精确的电流值。

3 仿真实验及分析

为了验证提出方法的可行性，使用Simulink 进行仿真实验。选用6 个额定电压为3.2 V，额定容量为3.2 Ah 的锂离子电池，组成电池组作为均衡对象，记作Cell-1、Cell-2 等。为了体现本文模糊逻辑控制算法先进性，选择与均值差分算法对比，分别进行静置均衡和充放电均衡两组实验。

3.1 静置均衡实验

图7 为基于均值差分算法和基于模糊逻辑控制算法(FLC)进行均衡的各单体SOC变化曲线。具体数据见表3。

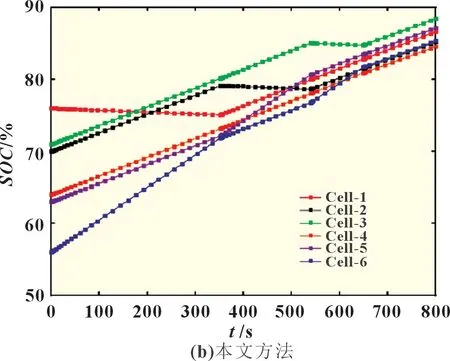
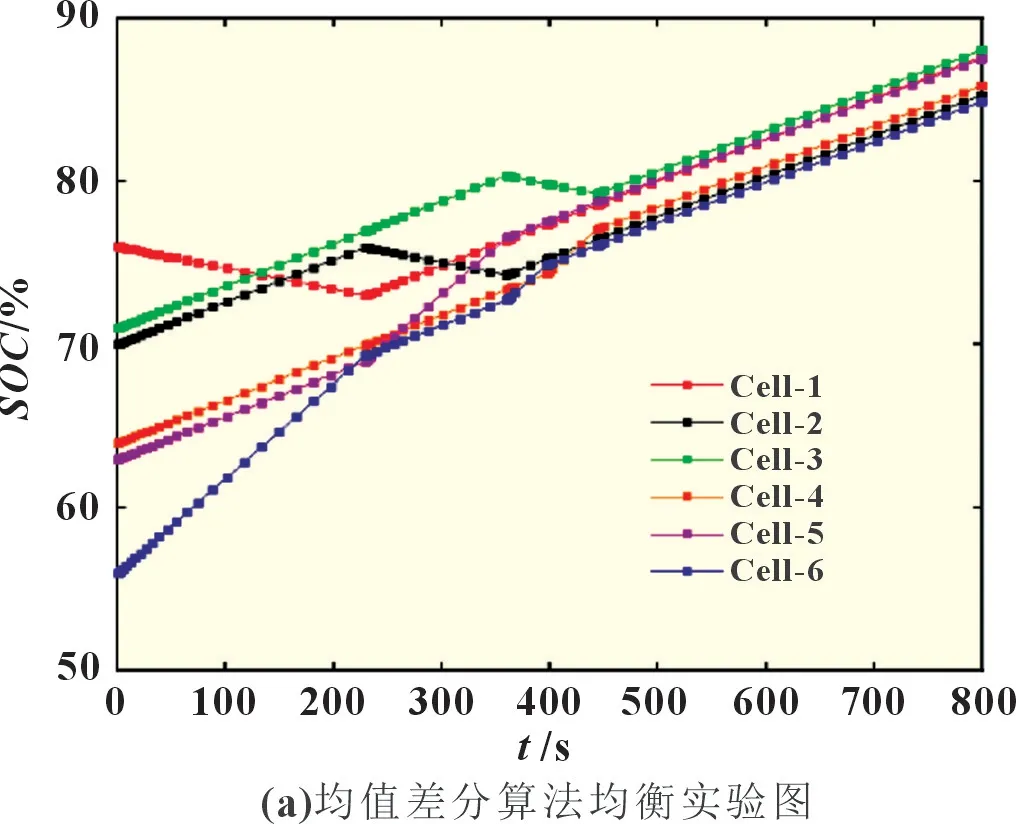
图7 静置均衡

在静置均衡的情况下，均值差分算法对电池组进行均衡需要688 s，而本文提出的方法只需要432 s，相比时间缩短了37.21%。由表3 所示的实验数据可知，使用均值差分算法进行均衡后的电池组平均SOC为64.78%，单体电池间的极差为4.84%；而使用本文方法进行均衡后的电池组平均SOC为66.17%，单体电池间的极差为2.81%。相比均值差分算法，本文方法的均衡效果提升明显。

表3 静置均衡对比实验结果 %

3.2 充放电均衡

图8 和图9 分别为基于均值差分算法和本文方法进行均衡充放电实验的各单体SOC变化曲线。具体数据见表4 和表5。

表5 放电均衡数据 %

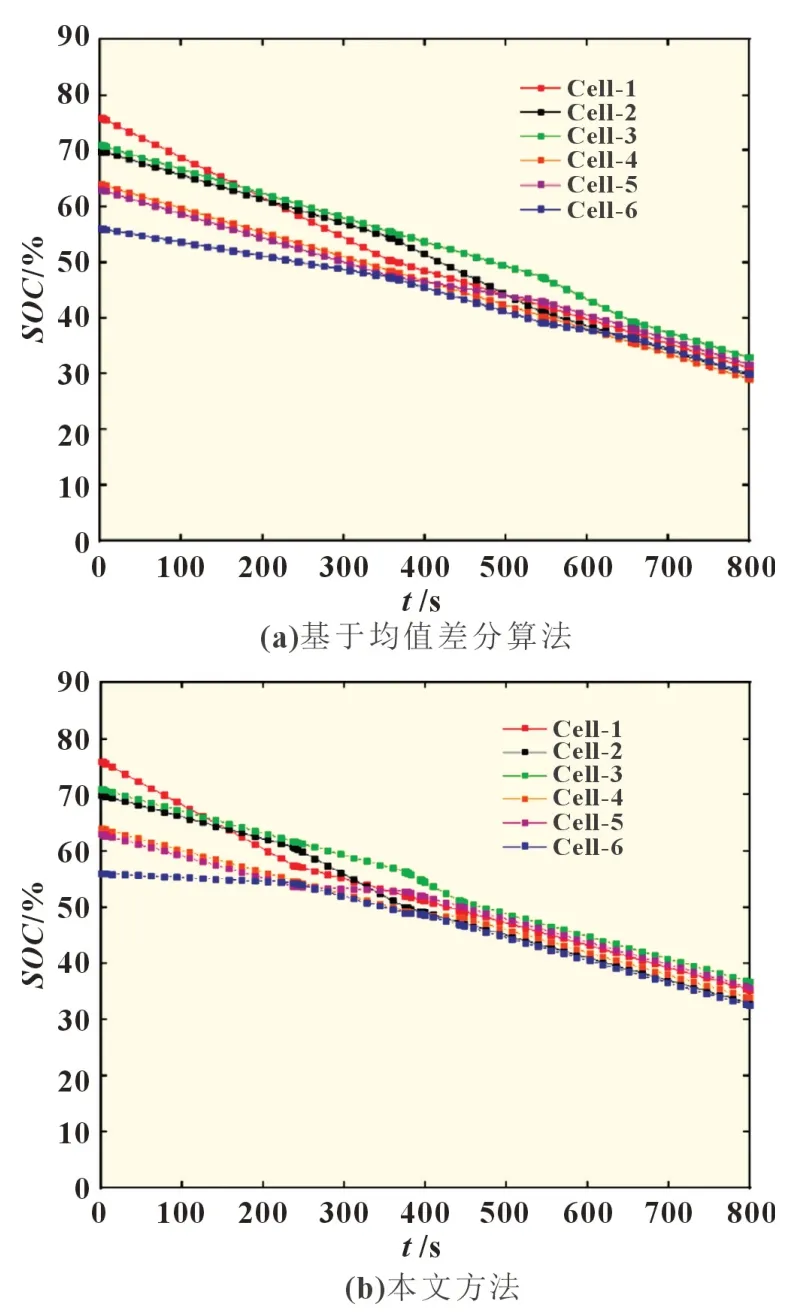
图8 充电均衡

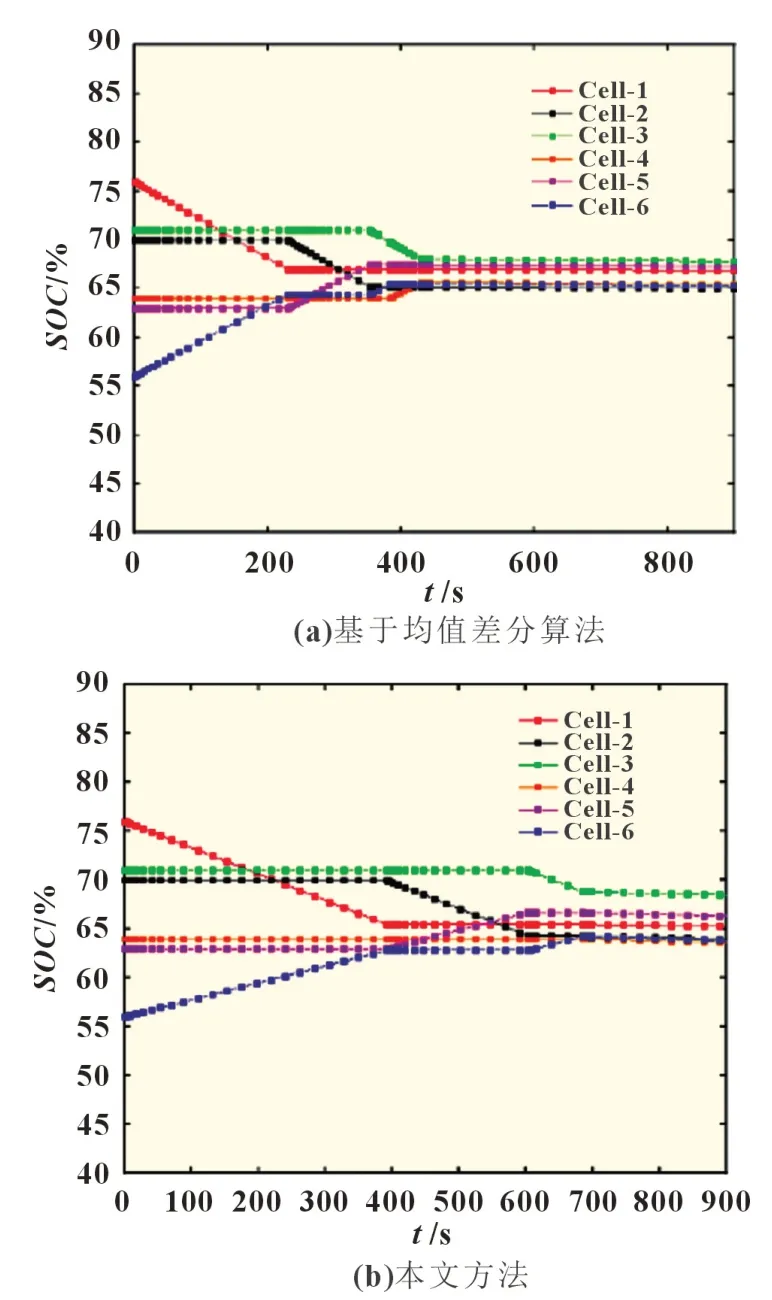
图9 放电均衡

表4 充电均衡数据 %

从图7 和8 看到，充电均衡时，使用本文方法所需时间为451 s，相比使用均值差分算法所需的652 s 缩短了30.8%。放电均衡时，使用本文方法所需时间441 s，相比使用均值差分算法所需的654 s 缩短了32.6%。

由表4 和表5 可知，充电均衡时，使用本文方法均衡后的平均SOC为86.59%，单体电池间的极差为3.17%，使用均值差分算法的平均SOC为85.59%，单体电池间的极差为3.88%。放电均衡时，使用本文方法均衡后的平均SOC为34.50%，单体电池间的极差为4.26%，使用均值差分算法的平均SOC为30.68，单体电池间的极差为3.82%。

由此可知，无论是静置均衡还是充放电均衡，使用本文方法都可以明显地提高均衡效率。

4 结论

为了减少锂离子电池组中串联单体电池之间的不一致性对电池组的影响，设计了一种可以在任意单体电池间进行均衡的拓扑结构。该拓扑能够缩短双向DC/DC 电路在相邻单体电池间进行均衡时所需要的时间，还能减少能量损耗。通过对电池SOC和电压曲线特性的分析，将均衡周期进行分段，选择电压和SOC作为均衡控制变量，制定了模糊控制规则。进行了均值差分法和本文方法的静态和充放电仿真实验对比。实验结果表明，本文提出的方法相比均值差分法所需时间减少了30%以上，能量消耗也有所减少。可以缩短均衡所需时间，提高均衡效率。