基于SVDF的多变量预测控制算法及应用研究
郑 鑫,克金超,陈亚萌,段艳旭,谢 磊
(1.中电商丘热电有限公司,商丘 476000;2.浙江大学 控制学院,杭州 310027)
0 引言
模型预测控制(MPC)是近几十年来最具代表性的先进过程控制技术之一[1]。MPC由预测模型、反馈校正以及滚动优化这三大基本模块构成,其主要思想是根据一个明确的过程模型预测系统的未来响应。在每个控制周期内,MPC在有限的控制范围内计算未来一段时间最优的操纵变量增量,以优化未来行为。相对于传统的比例积分微分(PID)控制[2],MPC的优势在于其可以处理约束,且对于多输入多输出控制系统有着良好的控制效果。MPC为不确定性、约束、非线性广泛存在的复杂工业过程控制提供了新的解决思路。经过30多年的发展后,MPC已经在工业过程控制中得到了广泛的使用与认可,并逐步被应用至能源[3]、航空航天工程[4]、和汽车工业[5]等领域。
随着工业过程中被控对象变量个数的增加以及工业过程中嵌入式设备的发展,实际应用中一些工厂对控制的时效性提出了更为严格要求[6],因此近年来对于在线MPC计算问题的关注度越来越高,在系统的采样间隔内,如何在保障控制性能的条件下快速地计算获得满足约束的MPC解成为了研究热点[7]。国内外众多学者进行了相关研究以提高MPC 在线计算速度从而解决上述问题。目前主要可以分为两类算法:其一是对 MPC 算法进行改进以简化在线计算,代表方法是Bemporad[8]在2002年提出的显示模型预测控制算法。该算法分为离线计算与在线优化两个部分。显示模型预测控制算法首先离线地对状态空间进行划分,并为各个子空间设计合理的线性控制律。状态分区与对应的控制律将被保存至存储器并提供给在线优化用以节省部分在线计算量。然而,随着问题规模的增大,显而易见的是状态分区与控制律会随之呈现指数增长趋势,这将会对存储量提出挑战。因此,显示模型预测控制只适用于控制维数较低的系统。其二则是开发高效的优化问题求解策略从而提高在线求解速度,目前主要为有效集算法[9]、内点法[10]以及他们的衍生算法如:不可行有效集法[11],对偶有效集法[12]、惩罚函数内点算法[13]等等。
本文为多变量过程提出了基于奇异值分解的快速(SVDF)模型预测控制算法,首先利用状态空间方程递推获得系统的预测输出,形成二次规划问题;随后考虑到优化问题Hessian矩阵的不变性,对该矩阵离线地进行SVD分解以提取特征信息,并通过矩阵变化将原优化问题转移到共轭空间,随后引入SVDF方法从无约束最优解中选取满足约束的次优解,结束本次在线计算。通过MATLAB仿真与将所提算法与其内置内点法计算函数进行比较以验证算法的快速与有效性;最后,将所提算法应用于一双输入双输出的水箱系统液位进行控制。
1 基于状态空间模型的MPC
考虑如下的线性模型所表示的系统:
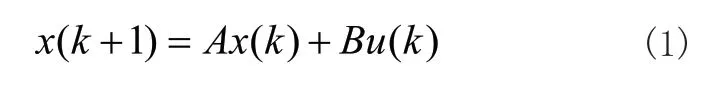
其中x(k)∈Rnx和u(k)∈Rnu分别是系统在k时刻的状态和输入变量。模型预测控制的目标函数为:


其中Q和R为正定矩阵,且满足:分别是有限时域下的预测状态集合和输入集合,有:

其中Np表示预测时域和控制时域。
由线性模型式(1)可以递推得到如下预测状态与输入之间的关系:

由于x(k)在每一个时刻已知,目标函数式(2)随后可以使用这一关系式(5)进行替换从而消除预测状态,变为只有预测输入相关的函数:

2 基于SVD分解的快速MPC方法
2.1 无约束解
注意到由于模型不改变,则F矩阵在预测过程中保持不变,如果权重系数矩阵Q和R在计算过程中不更改,则该目标函数的Hessian矩阵H同样也会保持不变。此外,H还是一个正定对称的矩阵,目标函数是一个二次函数。假设对输入做如下线性变换,从而将其投影到一个新的空间:

其中t是Hessian矩阵H的共轭向量集且满足
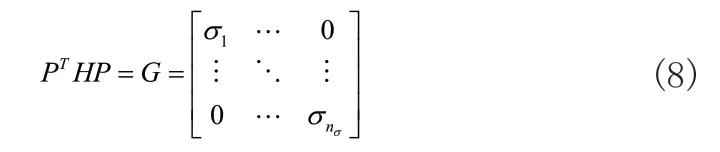
其中σi是Hessian矩阵的特征值且满足

P是Hessian矩阵的SVD分解得到的共轭矩阵。
则原目标函数(6)可以转化为其共轭空间形式:
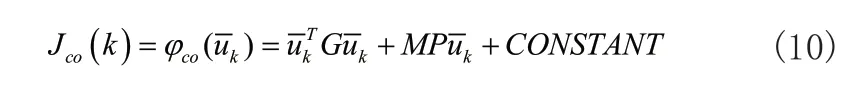
在不存在约束的情况下,共轭空间的最优无约束解可以直接得到:

通过使用式(7)进行简单的矩阵变换即可获得实际空间中的无约束最优解。
2.2 有约束解
在实际应用中,系统往往存在着各种各样的约束,在MPC的运行过程中需要考虑这些约束以保障设备的运行安全。由于输入与输出之间存在着显式的关系,系统约束可以由式(12)所示:

即MPC此时应该解决一个如下的优化问题

在处理过程约束时最简单直观的做法是将不可行解使得约束违反的部分移动到其边界上,然而,这种粗暴的方式往往会使得获得的解控制性能极差,根本达不到所需要的控制效果。因此需要考虑其他的约束处理方式。在上一节可以通过对Hessian矩阵进行SVD分解,随后通过矩阵变化将原空间优化问题投影到其共轭空间中。在此框架下,可以利用共轭空间中的无约束最优解,在不需要求解优化问题的情况下,获得一个满足约束条件的次优解。首先将优化问题中目标函数写作的形式如式(14)所示:

基于上述分析,我们对共轭空间中的无约束最优解执行如下操作以实现对于次优解的线性搜索。
按照特征值大小从大到小将对应的共轭空间无约束最优解的元素置0,直至满足约束条件,定义此时的元素编号为r,则共轭空间次优解应该存在于Ur与Ur+1之间,其中:

λ需要满足下述关系:

综上,基于SVD分解的快速MPC方法总结如表2所示。

表2 基于奇异值分解的快速MPC方法 (SVDF MPC)
3 仿真研究
本文首先使用一个双输入双输出的简化版蒸馏塔模型[14]在MATLAB上进行仿真以验证算法的有效性与快速性。模型具体描述为:

其中u1为回流量,u2为蒸馏塔塔顶蒸汽流量。y1为该蒸馏塔第21块塔板的温度,y2为该蒸馏塔第7块塔板的温度。为了保障蒸馏塔的安全性,尽可能地增加设备使用寿命,该蒸馏塔在运行过程中存在式(20)的约束:

MPC的权重矩阵选取为Q=100,R=0.01,预测时域与控制时域均选取为100。其余仿真参数如表3所示。
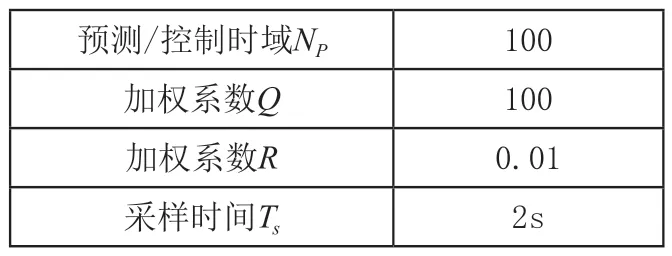
表3 仿真参数
为了体现算法优势,同时使用所提算法与MATLAB内置函数quadprog对优化问题进行计算。quadprog使用内点法对二次规划问题计算。
仿真结果如图1~图5所示。

图1 SVDF与内点法的多变量预测控制被控输出比较

图2 SVDF与内点法的多变量预测控制被控输出比较

图3 SVDF与内点法的多变量预测控制控制增量比较

图4 SVDF与内点法的多变量预测控制迭代次数比较

图5 GPAD与内点法的多变量预测控制执行时间比较
可以看到所提出的快速MPC方法能够获得与quadprog相似的控制结果,二者都能够跟踪上所设定的目标值。二者在仿真时间内的平均计算时间如表4所示。

表4 实验参数
可以看出所提的快速MPC算法计算更为迅速,体现出了算法的快速性。
4 双输入双输出水箱实验研究
4.1 双容水箱模型及实验参数
实验选用CS4000过程控制实验装置,控制器为Rockwell的PLC,对装置中的两个水箱进行液位控制,采用主回路调节阀与副回路变频器两支回路管道同时供水作为流入量,水箱结构如图6所示。
图6中h1表示一号水箱液位,单位为厘米,二号水箱液位用h2标注,主回路输入到一号水箱中的流入量为Q1、输入到二号水箱的流入量为Q2、副回路的水流只流入到二号水箱中,流入量为Q3、一号水箱的流出量为Q4、二号水箱的流出量为Q5,流量的单位为cm3/s。

图6 双容水箱结构图
经过辨识,该双容水箱模型为:

其中:
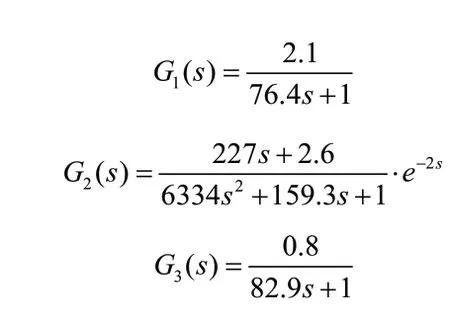
实验过程中算法的其他参数选择如表4所示。
此外,为了保障设备安全性,对于本实验施加的约束如式(21)所示:

4.2 实验结果
为了验证所提SVDF算法的有效性与快速性,对双容水箱的液位设定值进行改变并交由算法进行跟踪。在无外界干扰的情况下,实验得到结果如图7~图9所示:

图7 一号水箱液位变化

图8 二号水箱液位变化

图9 双容水箱控制增量变化
可以看到,对双容水箱实验应用基于SVD的快速MPC算法同样取得了比较好的实现效果,无论是一号水箱的液位h1还是二号水箱的液位h2都可以快速准确地跟踪到给定地设定值。此外,在运行过程中,系统输入都能够保持在约束范围之内。
5 结语
本文考虑到多变量预测问题Hessian矩阵的在线不变性,基于奇异值分解提出了一种可以实现快速在线计算的次优解计算算法SVDF。通过应用所提出的SVDF算法,可以极大地提高多变量预测控制问题的在线计算速度。首先使用MATLAB平台仿真证实了所提算法相较于内点法计算方法的快速性和准确性,随后基于PLC平台对双容水箱液位进行控制,可以由实验结果看到所提算法在PLC平台上同样具有优良的控制性能。

