基于天波重构技术的eLORAN信号周期识别算法
刘时尧 华 宇 张首刚
①(中国科学院国家授时中心 西安 710600)
②(中国科学院精密导航定位与定时技术重点研究室 西安 710600)
③(中国科学院时间频率基准重点研究室 西安 710600)
④(中国科学院大学 北京 100049)
1 引言
罗兰(LOng RAnge Navigation, LORAN)C系统是美国海军于20世纪50年代出于军事目的而发展起来的陆基导航系统,是一种远程双曲线导航定位系统[1]。增强型罗兰(enhanced LORAN, eLORAN)是由Loran-C系统演变而来,其采用Eurofix数据链技术进行三态脉位调制(Pulse Position Modulation,PPM)实现增强数据信息发播[2],具有作用距离远、稳定性好、抗干扰能力强等优点。近年来,美国、韩国、英国、俄罗斯等多国均重新启动了新型eLORAN系统的建设研究,而我国也于2017年启动了“高精度地基授时系统”项目,旨在成为北斗卫星系统的可靠地基备份以完善我国的星地一体化高精度定位、导航、授时(Positioning, Navigation and Timing, PNT)系统。
周期识别是信号处理中的核心问题,其稳定性极易受到天波、连续波、交叉干扰以及各种噪声的影响,可能引起跳周(1载波周期=10 μs)。另外,对于添加了数据调制的eLORAN信号,很容易因为将天波信号误捕获为地波而造成解码误码率增大,最终导致授时错误及导航定位的极大误差。天波干扰指的是经过电离层反射的天波辐射信号与地面波间接收时延差小于信号的有效时长时对地面波造成的重叠效应[3]。根据国际海事无线电技术委员会(Radio Technical Commission for Maritime, RTCM)发布的长波接收机最低性能标准,天波一般位于地波信号后的37.5~1500 μs[4]。为了保证PNT精度,eLORAN接收机要求利用地波信号进行周期识别,因此一般将地波脉冲组第1个脉冲的第3载波周期正向过0点(30 μs处)作为标准过0点。
近年来出现了不少周期识别算法的研究[5—9],包括优化包络相关法、多径估计延迟锁定环(Multipath Estimation Delay Lock Loop, MEDLL)算法等,但均是单纯针对寻找标准过0点的研究,而忽略了讨论如何判断天波干扰和地波识别问题。另外这些均是时域方法,容易受到各种强干扰而导致信号畸变,因此在恶劣条件下的适用性不高。针对以上难点,本文通过比较结合现有方法并提出联合算法,在低信噪比、强天波干扰环境下解决了天地波的识别问题,并在此基础上有效构造天波信号,利用去除天波后的伪地波成功实现周期识别,为后续解调解码等过程提供了保障。
2 信号体制
Loran-C信号以脉冲组的形式发射,而eLORAN信号与传统的Loran-C信号的区别主要是在第3~8个脉冲增加了数据调制,标准eLORAN脉冲时域波形用公式表示为[10]
实际中由于多跳天波离地波较远,因此只考虑距离较近的一跳天波的影响。受到一跳天波干扰的信号时域波形可用公式表示为
其中,sground(t),ssky(t),τg,τs,A,B分别为地波、天波信号及其时延差和幅值;n(t)为噪声干扰。
设定天地波时延差Δτ为100 μs,天地波幅度比(Sky-Ground Ratio, SGR)为6 dB并加以10 dB的白噪声,根据式(1)、式(2)可以得到eLORAN标准脉冲及混合信号波形如图1所示。
根据《船用罗兰C接收设备技术标准》[10],罗兰C信号的信噪比(Signal Noise Ratio, SNR)指信号接收电平与大气噪声均方根电平值之比,可用无量纲的数或分贝数表示。其中信号电平定义为脉冲包络起点之后25 μs处连续波有效值电平,本文之后的仿真SNR均是根据以上定义为标准。另外,信号进入接收机后,首先会经过梳状滤波器(40次左右线性累加),在保证信号不畸变的同时提高信噪比(15 dB左右),故文中的仿真SNR如无特别说明均是在天线接收端信噪比基础上增加15 dB后的结果。
3 算法描述
eLORAN接收机进行信号处理,实现高精度PNT功能是依赖地波信号的,而天波信号的混入会影响周期识别效果,造成以下两类致命的错误:(1)将天波误捕获为地波信号造成的地波识别错误;(2)天波影响地波的位置估计而导致的跳周错误。为了解决以上问题,提高寻找地波第3周过0点的准确度,本文对天波特性进行了深入分析,并提出了一种针对天波干扰的周期识别联合算法。该算法可以分为以下3个部分,如图2所示。
(1) 天地波识别模块。当天地波位置较近或天波信号较强时,加之各种噪声干扰等因素的影响,会造成地波识别错误,导致数十微秒甚至上百微秒级别的时延估计(Time Delay Estimation, TDE)误差并最终引起授时定位偏差。而该模块的目的正是在于将识别信号首先定位在地波信号上。
(2) 天地波分离模块。经研究发现,高强度的天波干扰会对地波的位置估计产生较大影响。因此,经天地波识别、决策后,需要进行天地波分离的信号进入此模块,通过自适应匹配算法得到天波的准确位置及强度并消除天波,得到较为干净的伪地波信号。
(3) 周期识别模块。该模块将对以上两个模块的输出结果进行进一步处理,利用基本无天波干扰的伪地波信号寻找到标准过零点位置,实现周期识别。
3.1 天地波识别模块
天地波识别模块的核心功能是判断天波的有无,而该过程的实现主要是利用信号时延差、幅度比估计,以及二者的相互关系进行分析判断。目前已经存在一些较为成熟的天地波时延差估计方法,包括多重信号分类(MUltiple SIgnal Classification,MUSIC), (Auto Regressive Moving Average,ARMA)及ESPRIT(Estimation of Signal Parameters via Rotational Invariance Techniques)算法等[11—14],都可以在不是很极端的信噪比环境下达到TDE需求。其中MUSIC算法分辨率更高,峰值更尖锐,但信噪比要求也最高;ARMA模型及ESPRIT算法抗噪能力稍强,但分辨率及估计准确度较差。但以上提到的算法均存在一个致命问题,即均是在“天波存在”假设下提出的技术,研究重点主要为天、地波的时延差估计,不能体现信号幅度特征,无法在盲测时利用幅度信息辅助判断是否存在天波。近年来的一些新的研究成果,如EXIP-WRELAX(EXtended Invariance Principle Weighted fourier transform and RELAXation)算法、神经网络算法等[15—17]也都存在同样的问题,因此在实际应用时容易受到天波或交叉干扰等影响而导致错捕或误识别且无法纠正,这也是目前各种接收终端中周期识别一直无法较好实现的关键所在。
经典频谱相除算法的最大优势在于可以较好地反映信号幅度特征,这是判断信号存在与否,实现天地波信号的识别功能的关键。因此本文对此算法进行了深入研究以改进其在强干扰环境下的分辨率及抗干扰性能要求。其基本原理推导为[18,19]
eLORAN信号的能量主要集中在85~115 kHz,因此在频谱相除算法中通常会使用窗函数以降低带外噪声及干扰。文献[18,19]均使用了带宽50 kHz的汉宁窗进行频域截断,但是此种窗在天地波时延差较小时由于分辨率不足而无法达到效果,因此本文对窗函数进行了改进。通过对各类窗函数的研究比较可以得到一致的结论:窗口越窄,去噪效果越好,IFFT变换后峰越平坦(分辨率低),估计越准确;反之,窗口越宽,峰越尖锐,分辨率越高,而去噪效果也越差。另外分析表明,窗函数的下降梯度越大,两侧越平坦,则干扰抑制能力越强。因此为了兼顾高分辨率和干扰抑制这两方面需求,可以在更宽窗口的基础上对其梯度进行优化。经过大量对比验证,本文选择了在式(4)中取140 kHz宽的Parzen窗及h=2.3,以提高窗口下降梯度并使带外部分更加平缓。根据以上改进,通过式(3)、式(4)步骤提取到了更恶劣条件下(SNR=5 dB(天线接收端—10 dB),SGR=18 dB, Δτ=38 μs)的天地波信息。
通过图3(a)可以看出,改进的Parzen窗在保证窗宽度的同时对梯度有了明显改善,图3(b)的峰信息对比也显示出改进窗的高分辨率可以成功将天波和地波区分开来,并维持了较好的去噪效果。但超过强天波阈值( Δτ≤60 μs, SGR>5 dB)的高强天波会严重影响TDE的准确度,加之窗函数引起δ峰左右两侧的旁瓣效应(Δτ<35.5 μs,分别小于—22 dB,—33 dB)及噪声干扰等会使TDE误差远大于5 μs。这对周期识别来说极其致命,同时也是以往许多研究中都无法克服的问题。另外,强噪声及其他台站的交叉干扰信号等造成的尖峰也可能会使真实信号峰被淹没,导致信号识别错误,故仅利用1次频谱相除的峰信息分辨天波和地波是缺乏可信度的。为此,本文基于大数法则的思想设计了天地波识别算法,其步骤如下:
(1) 利用捕获框将信号控制在采样数据中心附近,连续采集N组峰信息(建议不少于50组以保证样本数充足,每组1 ms),累加并取极大值点Pm,则由于信号已捕获,Pm必为天波或地波信号标识;在其左右各取1个次大峰Pl, Pr,计算并预存峰值比及时延差信息;
(2) 在每组峰信息中寻找最接近Pm位置的峰Qm(i),并在其左右各统计1个次大峰Ql(i)和Qr(i)共N组。若某侧存在信号,则应有大量次大峰集中在Pl或Pr附近,因此可分别统计此两点±10 μs范围内Ql(i)和Qr(i)的个数,利用经验个数阈值(可取N的50%~75%)分别判断左右两侧是否存在eLORAN信号,并根据旁瓣的幅度、位置特性排除将旁瓣误判为信号的可能性;
(3) 根据天波判断结果进行信号输出抉择:
(a) 若存在天波则根据信号时延关系确定天波、地波,并保存预估幅度比D、时延差 Δτ及等信息。由于弱天波干扰对地波的位置判断的影响不大,因此可根据前段提到的强天波阈值进行判决,将参数D和 Δτ在阈值范围内的信号输入天地波分离模块。
(b) 若判断无天波信号干扰或参数值在强天波阈值范围之外,则直接将当前信号及预估的地波位置信息τg0输入周期识别模块。
该模块是后续模块的基础,其准确率主要受交叉干扰、突发干扰及噪声的强度及频度的影响,其中窗函数及带通滤波器(Band-Pass Filter, BPF)可以高效抑制大量的带外干扰及噪声,而梳状滤波器可压制绝大多数的交叉干扰信号。另外,在接收设备非常接近某干扰台站时,交叉干扰信号强度也有可能高于远处台站的跟踪信号。此种情况下可同时捕获该干扰信号并利用其脉冲组重复周期关系对消大部分交叉干扰能量。
接收信号经过各种前端处理后,仍可能有少量无法预测的同频干扰或突发干扰等影响信号峰,因此在工程应用时应根据不同地点测试数据综合考虑并给出经验个数阈值以供接收设备设定。
该算法的计算复杂度主要取决于每组数据采样点数M,以及频谱相除和峰值检测等步骤。其中:傅里叶变换(Fast Fourier Transform, FFT)、IFFT的时间复杂度均为O(M ·log2M);除法及窗函数运算复杂度均为O(M);检测最大峰、次大峰的复杂度为O(M)。故利用N组峰信息进行天地波识别的时间复杂度为:O(N ·(2·M ·log2M+M)+N ·M+2·M+N ·M)=O(N ·M ·log2M)。相比于天地波分离模块所需的10 MHz采样率,此模块对采样率要求不高,在实际应用中可使用现有接收机通常使用的2 MHz采样率以节省80%的计算量。以上算法利用了大数法则的理论,利用多组峰信息并选择合适的个数阈值进行联合判决,极好地解决了交叉干扰、同频干扰以及其他突发干扰的影响,在利用模拟源及新型接收终端进行测试时几乎没有出现过错误,较好地实现了不同天波干扰环境下的天地波识别,准确地将捕获框锁定在地波信号上。
3.2 天地波分离模块
天地波分离的核心是准确地重构天波,而强天波干扰会极大影响地波的位置估计精度,使TDE误差大于5 μs并导致周期识别跳周。针对此问题,本文设计了自适应去天波算法,包含了两阶搜索过程以及用于匹配的混合信号幅度2维网格,以保证准确估计天波时延τs及幅度B的同时尽可能节省计算量。其中网格中映射的数值为无干扰、无噪声环境下不同幅度(范围0.1~18倍,步长0.1)、时延差(范围37.5~200 μs,步长0.1 μs)天波干扰下的混合信号幅值,由仿真软件生成后存储于DSP存储器中。该算法其流程图如图4所示,并包括如图4的步骤。
(1) 将预估的时延差Δτ及幅度比D与预存的混合信号幅度网格C进行匹配,根据其数值与经过带通滤波器的实际信号幅度间的比例关系以及 Δτ的搜索范围,通过式(5)预估出第1阶搜索中时延循环对应的天波幅度搜索中心B0(k)。由于不同时延差对应的天波幅度估计初值差别可能较大,因此,在第1阶段时延差循环中得到不同的B0(k)可以达到缩小幅度循环范围,提高效率的目的
(2) 以τs0,B0(k)为中心进行第1阶段搜索,选择相对较宽的搜索范围以及较大的步长循环构造并去除伪天波,得到伪地波组;利用伪地波组的峰值信息与基准信号组合并与伪地波组对消得到残差组并计算均方根(Root Mean Square, RMS),利用最小均方原则得到粗略的天波时延差及幅度参数值,B′。
其中,信号输入接收机后会进行电平调整,故本文后续仿真统一将采样信号幅度标准化为10,并选择10 MHz采样率以满足天波幅度及时延估计精度需求。另外,进入此模块的信号中天波功率相对较大,因此利用频谱相除技术时对天波参数的估计误差相对较小,时延误差范围一般不超过5 μs,而幅度误差一般不超过25%。据此,两阶段搜索范围及步长推荐设置如下:
根据上文中天地波分离模块的详细步骤说明以及图4的具体实现流程,式(6)—式(9)结合各过程变量给出了几处关键节点的计算方法,其中式(6)、式(7)表示两阶搜索中伪天波对消、伪地波对消及残差RMS的循环计算方法;式(8)、式(9)为构造最优伪天波、产生最优伪地波的计算方法
根据图5(a)所示,去天波前的天、地波时延估计分别为138.9 μs, 95.0 μs,与真实值偏差分别为1.1 μs, 5.0 μs,天地波幅度比D估计为2.1562。而运用本节提出的天波分离算法后,根据仿真过程量可知天波时延估计误差为0,幅度比估计为2.0662,偏差为3.31%,即基本上去除了天波,如图5(b)、图5(c)所示。
3.3 周期识别模块
以上两个模块成功地实现了天地波的识别和分离,极大降低了天波干扰的影响并准确定位地波信号。而周期识别模块的目的是准确寻找伪地波信号的标准过零点,其中的关键正是识别正确的载波周期。目前对此问题的方法研究主要分为以下两类:
(1) 时域方法:周期累加值法、波形匹配法、优化包络相关算法、MEDLL算法等。
时域算法对信噪比要求较高,其中周期累加值法、周期和值法、波形匹配法的信噪比下限为23~25 dB;峰值比算法有了一定的性能提升,在信噪比达到15 dB 以上时能够有效检测标准过0点[9],因此有一定的工程应用价值;包络相关算法分辨率较低,容易受到波形畸变影响且计算量相对较大;MEDLL算法在包络相关算法的基础上结合了包络求导技术[6],一定程度提高了分辨率及信噪比性能,但当信噪比低于14 dB或天波过强时甚至无法分辨。
(2) 变换域方法:MUSIC算法、ARMA模型、ESPRIT算法、IFFT频谱相除算法等。
相对于时域算法,各种变换域方法复杂度更高,但在信噪比条件及稳定性方面有着明显优势,3.1节总结了几种方法的性能特点。其中,ARMA模型及ESPRIT算法抗噪能力稍强,但分辨率及估计准确度较差,容易导致跳周;MUSIC算法及频谱相除算法相对稳定,在天波干扰较小时估计精确度极高,但MUSIC算法的信噪比要求相对较高[14]且计算量更大。
经过对上述算法理论的深入分析可以看出,各种时域算法较为简单实用,但对信号接收环境有较高的要求。如峰值比算法,在噪声及干扰环境适宜时有较高的稳定性,但也容易受到天波残差以及各种噪声干扰引起的波形畸变的影响,导致跳周错误,在工程应用中可结合环境估计结果决策使用。而本文研究重点为恶劣环境下的周期识别,噪声环境较差,因此更适合变换域方法。下文选择了其中稳定性高,计算量相对较小且信噪比要求更低的频谱相除算法进行周期识别过程(经仿真章节验证,SNR下限接近—2 dB,远低于上述方法)。
利用频谱相除方法推算标准过零点位置的基本流程与其他各种算法大致相同,即首先识别正确的载波周期,再检测标准过零点位置,其具体步骤描述如下:
(1) 不需要天地波分离的信号在天地波识别后直接输入此模块,并将预存的地波位置τg0记为PA;对天地波分离模块输出的伪地波则利用频谱相除技术,预估信号的起始位置点PA。由于伪地波中的天波残差较小,对IFFT计算的分辨率要求不高,故可以在计算中选择较窄的窗函数以实现更大程度的噪声抑制,突出信号尖峰。
(2) 根据估计所得地波起始位置点PA推后30 μs预估第3载波周期过0点PB。虽然基本无天波干扰,但PA点的估计误差会导致PB点与准确的标准过0点PC之间存在一个小的偏差。
(3) 根据PB点位置寻找最接近PB点的载波正向近0点PC并作为推算的标准过0点。
根据以上方式继续对3.2节示例中输出的伪地波进行处理,可得信号位置信息如图6所示。
从幅度归一化位置估计对比图6(a)中可以看出,去除天波干扰后,伪地波信号的起始位置估计误差已控制在半个载波周期范围内(本例为0.3 μs),随后如图6(b)所示,点PC准确地标识了标准过0点的位置。该方法利用了频谱相除技术的高稳定性,后续仿真结果可以验证,在去除大部分天波干扰或无天波干扰时,利用伪地波可以得到精确的标准过0点位置以及地波的起始位置。
4 仿真实验及结果分析
第3节分解讨论了该自适应周期识别算法的各个模块。本节对整体算法进行了充分的仿真实验及结果展示,并对主要过程量进行了对比分析。其中,由于天地波识别算法在仿真实验及不同地点的拷机测试中均无出错,故没有给出实验数据。
根据eLORAN接收机的最低性能标准要求[4],当天线接收端信号SNR≥—10 dB, SGR≤12~26 dB,Δτ在37.5~60 μs范围时接收设备应能进入锁定状态,而新型eLORAN接收机更要求在此范围内能够成功解码。本文算法与3.1节提到的各种类似的变换域方法均有其信噪比极限,在噪声功率过大时噪声峰会淹没信号峰,算法有效性也会急剧下降。其中在利用不同的窗及BPF处理且保证信号不失真时,频谱相除算法信噪比下限不低于—2 dB(天线接收端—17 dB左右)。而在实际应用中,一般认为天线接收端信噪比小于0 dB时为低信噪比环境。基于以上分析,本文针对各种恶劣环境,对仿真中的可变参数作如下设计:
(1) 输入信号:标准eLORAN信号+天波信号+随机白噪声,采样率为10 MHz;
(2) 天地波时延差Δτ:38~60 μs,步长为1 μs;天地波幅度比D:SGR=0~24 dB,步长为6 dB;
(3) 信噪比SNR:0~10 dB(天线接收端—15~—5 dB),步长为1 dB。
本文在MATLAB2017环境下,独立调整各参数,并在不同情况下分别运行了1000次。由于篇幅所限,文中只展示了SGR=0 dB, 18 dB和24 dB几种情况下的部分仿真结果及数据统计,如表1所示。
表1体现了在SGR=0 dB时该算法极高的性能。由于算法运行过程中幅度比估计值超过强天波门限范围,因此跳过了天地波分离而直接进入周期识别模块。结果表明,此方式在节省了效率的同时非常有效地实现了周期识别,验证了算法的合理性。
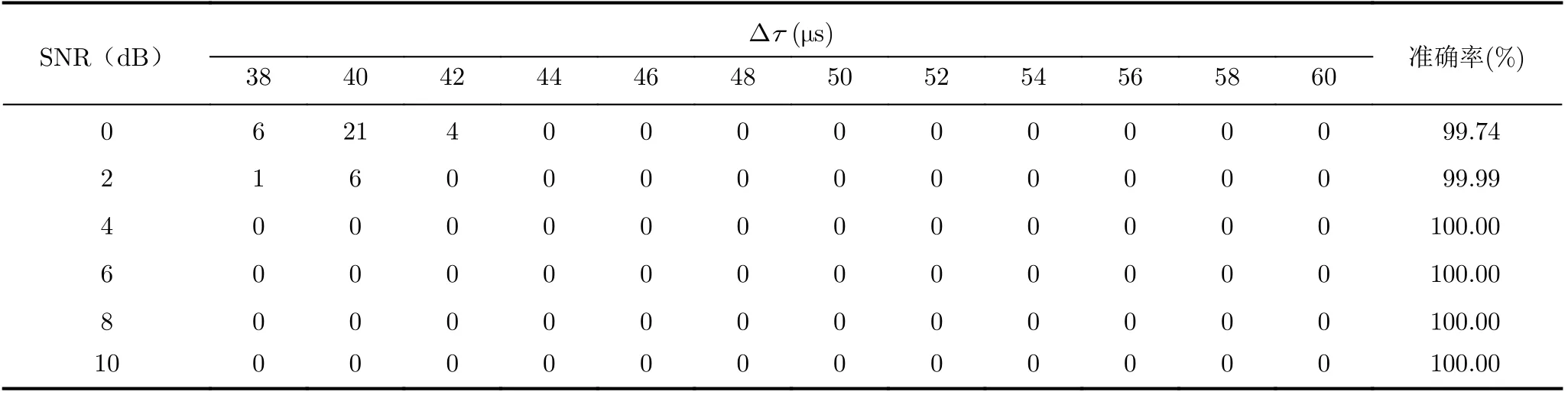
表1 周期识别错误次数及准确率(SGR=0 dB)
图7、图8分别展示了SGR=18 dB和24 dB时的天波位置及幅度的估计误差。可以看出,位置和幅度的估计精度随着SNR的增加而提升。经统计,位置误差RMS最大值分别为0.0126 μs和0.0105 μs,幅值误差率RMS最大值分别为1.09%和0.53%。通过对两个参数非常准确的估计,可以有效地重构并去除天波。
通过3.1节讨论可知,在强天波干扰环境下,改进前的频谱相除技术甚至无法区分天地波,即使改进了窗函数提高分辨率也仍存在极大的位置误差,导致周期识别跳周频发;而如表2、表3所示,经过了天地波分离过程,极大地提高了在不同条件下周期识别的正确率,基本高于99%。
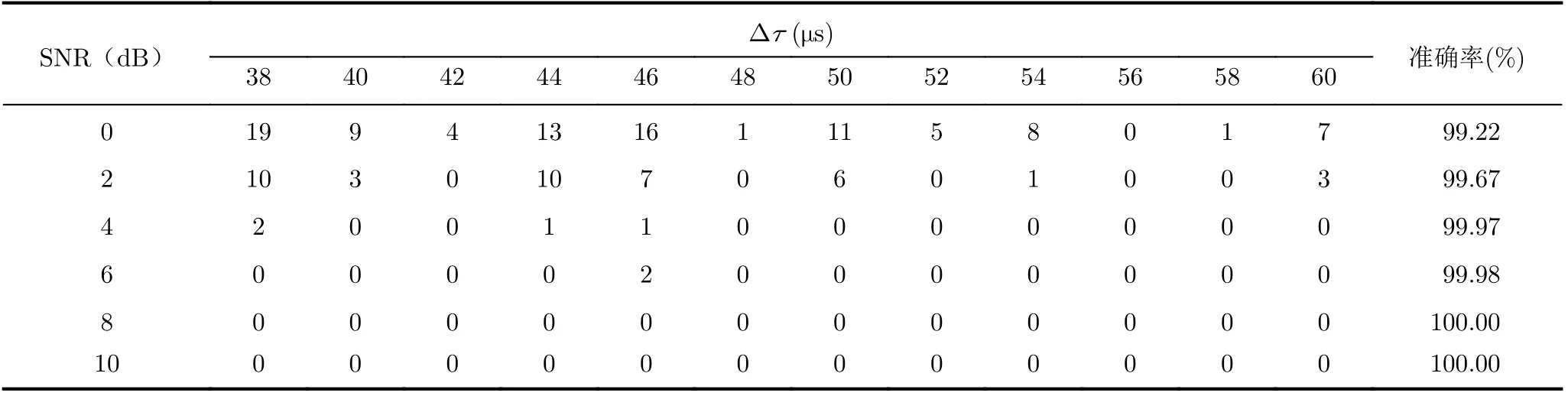
表2 天地波分离后周期识别错误次数及准确率(SGR=18 dB)

表3 天地波分离后周期识别错误次数及准确率(SGR=24 dB)
5 结论
本文所提联合算法主要是针对各种恶劣环境所设计,这也是目前各种周期识别算法研究的难点所在。根据上文的算法讨论和部分仿真结果展示以及更多的仿真数据统计,可以得出以下结论:
(1) 对窗函数的改进效果明显,有效地将高强度天波干扰下的eLORAN天、地波信号区分开来,并可适配提出的天地波识别算法,成功实现对天、地波信号的准确定位。另外通过决策过程准确判断是否需要进行天波分离,大幅节省了后续过程的计算量;
(2) 对天波的参数估计准确度指标均随SNR及天地波时延差的增加而提高,在极端恶劣的噪声及天波干扰环境下仍然能够达到极高的水平,且本文所提2阶搜索方式在大幅提高效率的同时可以有效地重构并去除天波信号,输出较为稳定的伪地波信号;
(3) 本联合算法可以保证在接收天线输入端SNR=—15 dB的极低信噪比下也能够保持极高的水准,周期识别准确率基本超过99%,完全可以满足新型eLORAN接收机的需求。
eLORAN接收终端的PNT精度很大程度上取决于周期识别的准确度,但高强度的天波干扰一直是信号处理中的一个关键问题,严重限制了周期识别算法的完整性及有效性。针对这一问题,本文提出一种自适应天波识别、分离和周期识别的联合算法。经过理论分析和各种不同接收环境下的仿真实验,验证了算法的可行性。本算法首先克服了经典IFFT频谱相除算法无法同时兼顾高分辨率和时延估计准确度需求的弊端,并结合其能够体现信号幅度特征的特点,有效解决了以往研究中常被忽略的天地波信号识别问题。其次,能够在恶劣的条件下成功将天地波的识别、估计、分离及寻找标准过零点等过程有机结合,在提高效率的同时保证了周期识别的正确率,具有良好的鲁棒性和可实现性。同时,精确的天波估计,也为接收机处理交叉干扰,提高解调解码的成功率提出了新的思路和理论参考。

