冲击参数对TC4钛合金模拟叶片损伤有限元模拟研究

张克瑶，杨雅丽，孙 阳，黄永芳，陈立杰

(厦门大学航空航天学院，福建厦门 361005)

1 引言

飞机起飞和降落过程中，航空发动机高速气流通道内不可避免地会吸入诸如砂石、金属碎片等硬度较大的颗粒外物[1]。外物与高速旋转的风扇/压气机叶片发生撞击，会导致叶片遭受外物损伤(FOD)[2-3]；而叶片在高/低周复合疲劳载荷的作用下[4]，FOD造成的微缺口、微裂纹、较大残余应力位置，均为可能的疲劳源[5]，将严重影响叶片的使用寿命。

国内外学者对典型叶片材料的FOD 进行了大量的试验和数值模拟研究。孙护国[6]和Xie[7]等采用Johnson-Cook 模型，分别对前缘半径不同的TC4 模拟叶片和航空发动机压气机叶片进行了FOD 数值模拟，研究了损伤尺寸随冲击角度、冲击速度及冲击小球直径的变化规律，但均缺乏试验结果验证。Lin等[8]采用Johnson-Cook模型，对Ti-6Al-4V模拟叶片分别进行了冲击角度为0°和45°的FOD数值模拟(冲击物为3 mm的立方体，冲击速度为250 m/s)，得到的冲击坑形貌及试件残余应力分布，与测试结果吻合较好。Luo 等[9]采用Johnson-Cook 模型，对TC4 平板试件进行了FOD 数值模拟(冲击物为2 mm 的钢珠，冲击速度为300 m/s，冲击角度为90°)，对比了有/无激光冲击强化对FOD的影响，分析了残余应力对试件疲劳强度的影响。赵振华等[10]采用Johnson-Cook模型，对考虑叶片前缘特征的TC4模拟叶片，进行了不同冲击角度下的FOD数值模拟(冲击物为3 mm的钢珠，冲击速度为250 m/s)，结果表明，随着入射角度的增大，试件残余拉应力区域变大，最大残余拉应力减小。综上所述，冲击产生的残余应力对叶片的疲劳寿命有一定影响，但目前已有研究主要集中在不同冲击参数对材料损伤的影响上，在冲击参数对残余应力分布规律的影响方面缺少全面深入的研究。

本文基于LS-DYNA软件，采用Johnson-Cook模型，考虑叶片叶型影响，对TC4钛合金模拟叶片进行FOD数值模拟，研究不同冲击参数下的残余应力分布。通过分析不同参数下的损伤形貌与残余应力分布情况，得到冲击角度、冲击速度以及冲击小球直径对损伤的影响规律，为叶片结构损伤容限设计提供了依据。

2 试件及损伤表征

2.1 TC4钛合金模拟试件

模拟叶片试件材料为TC4 钛合金，冲击小球原材料为GCr15 轴承钢，两种材料的基本性能参数如表1所示。

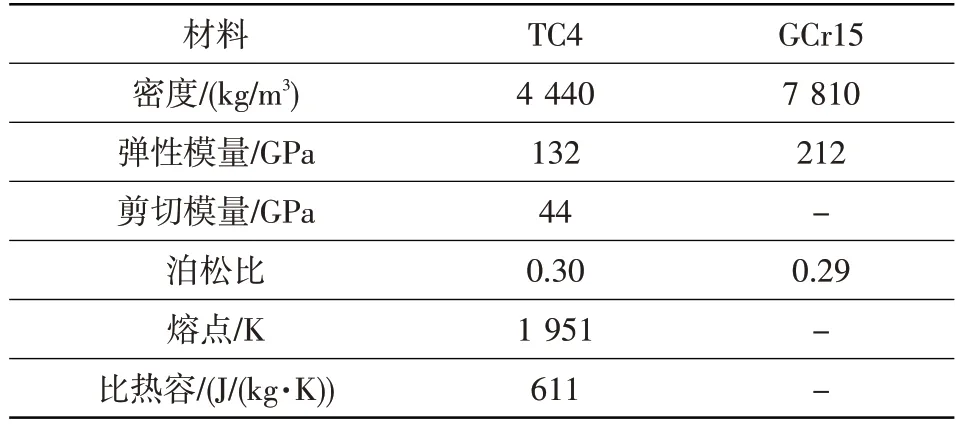
表1 模拟叶片与冲击小球材料性能参数Table 1 Material properties of simulate blade and impact ball

考虑实际叶型的影响，选择光滑模拟叶片作为试件。模拟叶片基本几何尺寸如图1(a)所示。叶片总长90 mm，中间10 mm 为模拟真实叶片前缘的冲击段，其横截面为椭圆形，横截面积为15.7 mm2。小球冲击方向如图1(b)所示。

图1 TC4模拟叶片Fig.1 TC4 simulated blade

2.2 损伤表征

冲击损伤件由中国航发北京航空材料研究院提供，采用空气炮试验系统进行FOD模拟试验。试验条件为：冲击角度0°，冲击速度350 m/s，冲击小球直径3 mm。采用Keyence VHX-5000 超景深3D 分析光学显微镜进行损伤表征。图2示出了模拟叶片典型的损伤形貌及损伤的宏观几何参数定义。试件损伤形式均为缺口型损伤，缺口形状为半圆形，部分冲击缺口边缘存在材料撕裂卷边现象。

图2 模拟叶片的典型损伤形貌Fig.2 Typical damage morphology of simulated blade

根据冲击试验得到35 个损伤样品的损伤检测结果，图3 为试验冲击缺口尺寸的箱型图及其分布。可看出，试验冲击缺口尺寸的分散性较大，特别是损伤深度，这可能是试验控制参数不准确造成的。为避免因控制因素而产生的数据离群值对后续分析造成影响，利用四分展布进行了异常数据剔除，剔除后试件冲击缺口的宽度、深度、长度的均值分别为3.06，2.32，1.93 mm，方差分别为0.009，0.076，0.047。

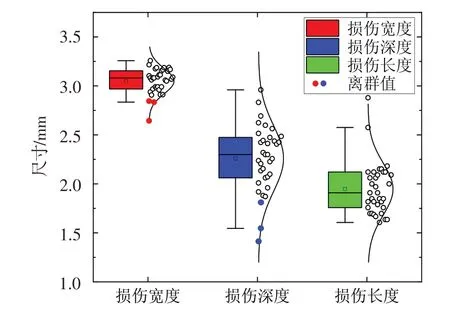
图3 试验冲击缺口尺寸箱型图及其分布Fig.3 Box diagrams and distributions of test impact notch sizes

3 外物损伤数值模拟

3.1 Johnson-Cook模型

基于LS-DYNA 软件，采用Johnson-Cook 模型，对模拟叶片进行FOD 数值模拟。其中，Johnson-Cook模型包括本构模型和失效模型。

(1)Johnson-Cook本构模型

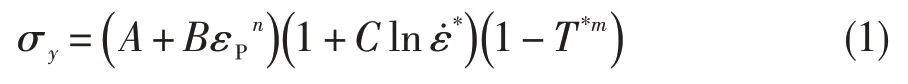
式中：σy为von Mises流动应力；A、B、n、C、m为材料参数；εP为等效塑性应变；为无量纲等效塑性应变率，为参考应变率；T*为无量纲温度，T*=(T-TY)/(Tm-TY)，TY为参考温度，Tm为材料熔点温度。

(2) Johnson-Cook失效模型

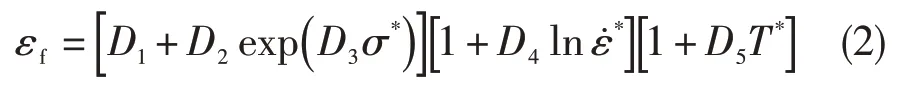
式中：εf为失效(塑性)应变；D1～D5为失效参数；σ*为静水压力与等效应力的比值，σ*=p/σeff=-σm/σeff，σm为平均应力。

对于TC4 钛合金的Johnson-Cook 模型：A取954.74 MPa，B取249.86 MPa，n取0.37，C取0.052 7，m取0.735，D1～D5依次取0.083 5、0.657 0、-2.090 0、0.014 0和3.800 0。

3.2 有限元模型

数值模拟过程选择mm-kg-ms单位制。对模拟叶片采用3D SOLID 164实体单元进行网格划分，选择逐渐加密的网格划分形式，对小球与模拟叶片碰撞的位置进行网格加密处理，设置最小网格尺寸约为0.06 mm，两端网格的最小尺寸逐渐增大。小球模型利用sphere solid 建立，选择3D SOLID 164 实体单元进行网格划分，网格尺寸约为0.10 mm。网格总数约为160 万。为防止初始穿透，设置小球与模拟叶片之间存在初始距离0.10 mm。为了模拟空气炮试验时模拟叶片的夹持方式，模拟叶片的边界条件设置为一端自由、另一端固支。根据空气炮试验结果发现，小球在冲击试验过程中没有发生形变，因此数值模拟时小球采用刚体模型，使小球模型区域刚体化，刚体域内节点、单元不发生相对运动。由于FOD 数值模拟过程中，模拟叶片上会发生材料失效行为，且需要删除失效单元，因此本文选择面-面侵蚀接触，基准惩罚刚度缩放系数取1.0。数值模拟过程系统阻尼选择默认值；忽略小球与模拟叶片之间的接触界面摩擦；选择标准LS-DYNA 黏性沙漏控制；设定总的求解时间为0.2 ms。

3.3 数值模拟结果与分析

3.3.1 数值模拟结果与试验结果对比

进行与2.2 节试验条件相同的FOD 数值模拟，结果如图4所示。模拟得到冲击缺口的宽度、深度、长度分别为3.07，1.62，2.00 mm。

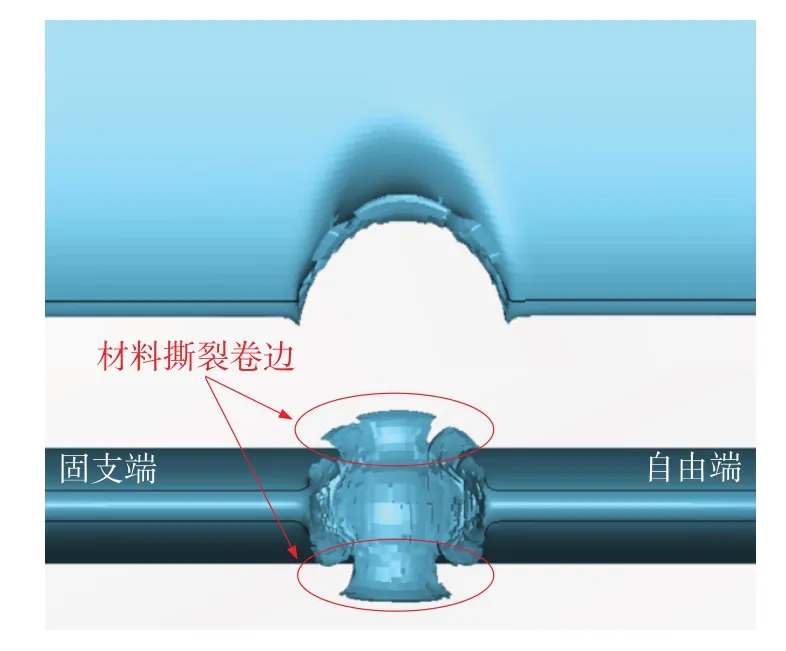
图4 FOD数值模拟结果Fig.4 Numerical simulation result of FOD

对比图2与图4可知，FOD数值模拟和冲击试验得到的损伤形貌均为缺口型损伤，缺口形状均为半圆形，且冲击缺口边缘处，也均存在材料撕裂卷边现象。FOD数值模拟与冲击试验冲击缺口的宽度和长度基本一致，相对误差较小，分别为0.320%和3.620%；深度的差别较大，相对误差为30.2%。综合上述分析，本文采用的有限元数值计算模型可以有效地用于FOD数值模拟。

3.3.2 冲击角度对模拟叶片FOD的影响

使用直径为1 mm的小球，以200 m/s的速度，对TC4 试件分别进行冲击角度为0°、30°、60°和90°的FOD数值模拟。图5给出了试件残余应力最大值随冲击角度的变化。可见，除冲击角度为0°外，随着冲击角度的增大，最大残余拉应力增大，最大表面残余拉应力减小，最大残余压应力和最大表面残余压应力的绝对值增大。随着冲击角度的增大，损伤形貌逐渐由缺口型变为凹坑型。冲击角度为0°、30°、60°和90°时，对应的冲击缺口深度依次为0.251，0.175，0.152，0.131 mm，均随冲击角度的增大而减小。

图5 不同冲击角度下的残余应力最大值Fig.5 Maximum residual stress at different impact angles

图6 给出了小球直径为1 mm，冲击速度为200 m/s，冲击角度分别为0°和30°时，试件的残余应力分布云图。冲击角度为0°时，冲击缺口根部次表层有较大的残余拉应力，冲击缺口附近的表面及次表层有大面积的残余压应力；在表面层，靠近小球出射方向一侧，存在明显局部较高的残余拉应力。随着冲击角度的增大，靠近小球出射方向一侧的残余压应力区域变大；靠近小球入射方向一侧的残余拉应力区域变大。冲击角度为90°时，试件表面存在较大范围的残余拉应力区域。冲击角度为30°时，最大残余拉应力的位置出现在入射端冲击缺口处；除此之外，最大残余拉应力均位于次表层冲击缺口边缘，冲击角度为0°时靠近试件自由端一侧，冲击角度为60°和90°时靠近试件固支端一侧。冲击角度增大后，最大残余压应力的位置，由表面层冲击缺口边缘转移到表面层冲击缺口根部附近。

图6 小球直径1 mm、冲击速度200 m/s时不同冲击角度的数值模拟结果Fig.6 Numerical simulation results for a ball of 1 mm diameter and 200 m/s with different impact angles

3.3.3 冲击速度对模拟叶片FOD的影响

使用直径为1 mm的小球，在0°冲击角度下，分别以200，250，300，350 m/s的冲击速度，对TC4试件进行FOD数值模拟。图7给出了试件残余应力最大值随冲击速度的变化。可见，最大残余拉应力有随冲击速度增大而增大的趋势。冲击速度为350 m/s时，试件的最大残余拉应力最大；冲击速度为300 m/s时，试件最大残余压应力的绝对值最大。另外，随着冲击速度的增大，冲击缺口及其深度逐渐增大，且缺口边缘开始出现材料卷边现象。冲击速度为200，250，300，350 m/s 时，对应的缺口深度依次为0.251，0.304，0.366，0.433 mm。

图7 不同冲击速度下的残余应力最大值Fig.7 Maximum residual stress at different impact velocities

图8 是小球直径为1 mm、冲击角度为0°、冲击速度为300 m/s时，试件的残余应力分布云图。对比图6(a)可看出，冲击速度增大，试件表面的残余拉应力区域变小，次表层的残余拉应力区域无较大变化；缺口表面层和试件表面的残余压应力区域变小，除此之外试件的残余压应力区域无较大改变。最大残余拉应力的位置受冲击速度的影响较小，均位于次表层冲击缺口边缘，冲击速度为200 m/s 时，靠近试件自由端一侧，冲击速度为300 m/s 时，靠近试件固支端一侧。但冲击速度增大后，最大残余压应力的位置，由表面层冲击缺口边缘转移到表面层冲击缺口根部附近。

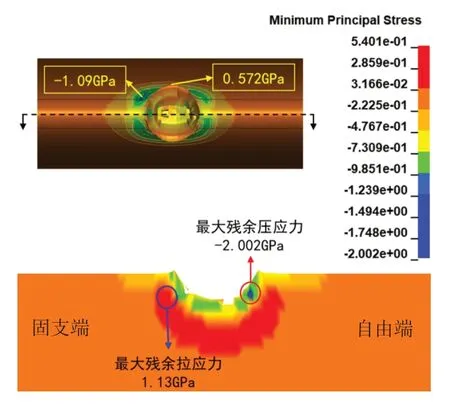
图8 小球直径为1 mm、冲击角度为0°、冲击速度为300 m/s时的数值模拟结果Fig.8 Numerical simulation results for a ball of 1 mm diameter and 300 m/s at 0°impact angle

3.3.4 冲击小球直径对模拟叶片FOD的影响

分别使用直径为1，2，3，4 mm的小球，在0°冲击角度下，以200 m/s 的冲击速度，对TC4 试件进行FOD数值模拟。图9给出了试件残余应力最大值随小球直径的变化。可见，最大残余压应力的绝对值有随小球直径增大而增大的趋势。小球直径为3 mm时，试件最大残余拉应力最大；小球直径为4 mm时，试件最大残余压应力的绝对值最大。另外，随着小球直径的增大，冲击缺口及其深度增大，且缺口形貌逐渐由半圆形转变为半椭圆形。小球直径为1，2，3，4 mm 时，对应的损伤深度依次为0.251，0.568，0.924，1.320 mm。

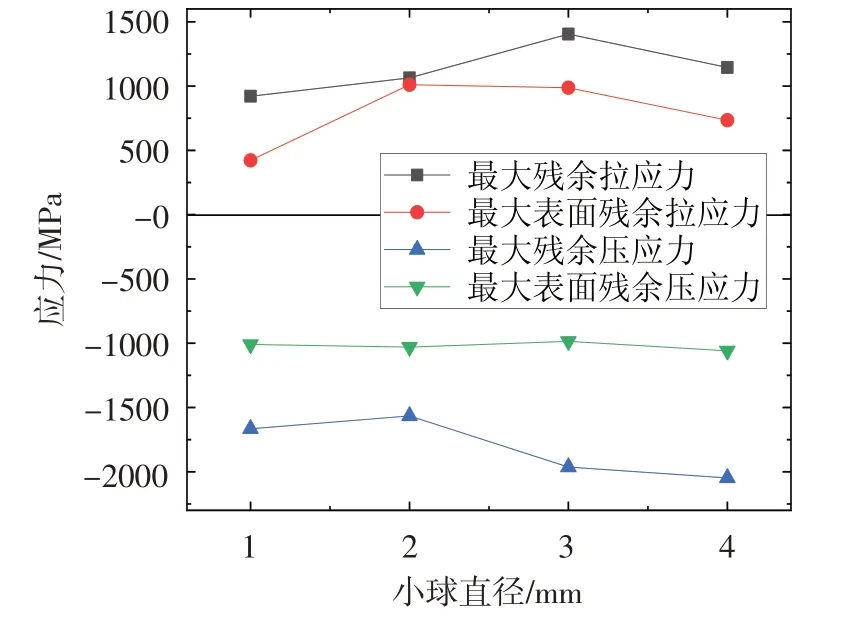
图9 不同小球直径时的残余应力最大值Fig.9 Maximum residual stress for the ball of different diameters

图10 是冲击角度为0°、冲击速度为200 m/s、小球直径为2 mm时，试件的残余应力分布云图。对比图6(a)可看出，小球直径增大，次表层的残余拉应力区域变小，次表层的残余压应力区域无较大改变，小球直径增大到2 mm时，试件表面存在较大范围的残余拉应力区域。最大残余拉应力的位置受小球直径的影响较小，均位于次表层冲击缺口边缘，小球直径为1 mm时靠近试件自由端一侧，小球直径为2 mm时靠近试件固支端一侧。但小球直径增大后，最大残余压应力的位置，由表面层冲击缺口边缘转移到表面层冲击缺口根部附近。

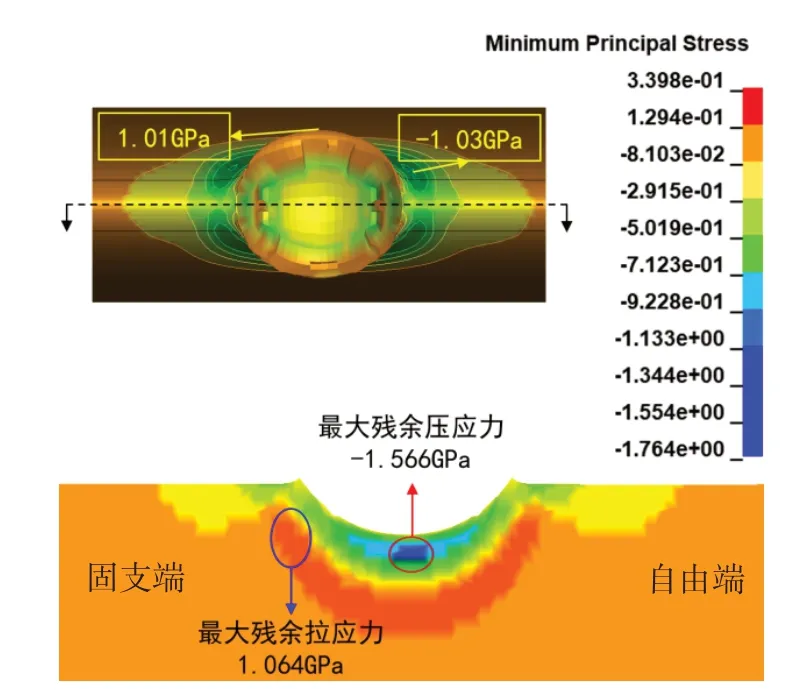
图10 冲击角度为0°、冲击速度为200 m/s、小球直径为2 mm时的数值模拟结果Fig.10 Numerical simulation results for a ball of 2 mm diameter and 200 m/s at 0°impact angle

3.3.5 冲击参数对模拟叶片FOD的影响

除冲击角度为0°外，随着冲击角度的增大，结构最大残余拉应力增大，位于次表层；最大残余压应力绝对值增大；冲击角度对最大残余拉应力出现位置的影响显著。冲击速度增大，结构最大残余拉应力随之增大，试件表面的残余拉应力区域随之变小，次表层的残余拉应力区域变化较小；冲击速度对最大残余拉应力出现位置的影响较小，均位于次表层冲击缺口边缘。冲击小球直径增大，结构最大残余压应力的绝对值有随之增大的趋势，次表层残余拉应力区域变小，残余压应力区域未发生显著改变；小球直径对最大残余拉应力出现位置的影响较小，均位于次表层冲击缺口边缘。冲击角度、冲击速度、小球直径对最大残余压应力出现位置的影响规律类似，三种冲击参数分别增大后，最大残余压应力的出现位置均由表面层冲击缺口边缘转移到表面层冲击缺口根部附近。

4 结论

采用数值模拟方法，研究了不同冲击参数对TC4 模拟叶片冲击损伤的影响，分析了模拟叶片的损伤形貌和残余应力分布状况，得到的主要结论为：冲击角度对残余拉应力的最值分布影响较大，冲击角度、冲击速度和小球直径对残余压应力的最值分布均有较大的影响。