航空发动机锥齿轮振动特性分析与试验验证
王艳丰,郜伟强,敬发宪,滕光蓉
(中国航发四川燃气涡轮研究院,四川绵阳 621010)
1 引言
航空发动机是一种非常复杂的旋转机械,其功率及转速经中央传动从动锥齿轮输出至附件传动齿轮箱,驱动发动机和飞机等相关附件工作[1]。发动机整个传动系统中,中央传动锥齿轮与发动机主轴靠近,相比其他齿轮具有运转速度高、工作状态复杂等特点[2];且随着高推重比发动机的研制,中央传统锥齿轮承受的机械力等载荷也越发复杂,其振动问题也越来越突出,资料显示WJ5AI发动机就曾发生过中央传动锥齿轮组件故障[3]。因此,研究中央传动锥齿轮的振动特性、减振和逼振方法,对于航空发动机的安全运行和可靠性具有非常重要的意义[4]。
齿轮振动特性的理论计算以及齿轮动应力和噪声测试,是掌握发动机齿轮工作状态中振动特性的有效手段。根据文献[5]报道,国内外对于齿轮动应力的理论计算和试验测量都已经取得一定的研究成果。其中,朱梓根[6]、晏砺堂[7]等对锥齿轮的横向振动特性进行了分析,并对齿轮的行波共振提出了新理论,表明固定啮合位置的锥齿轮旋转时,可能存在前、后行波节径共振。Houser等[8-9]通过试验测试研究了齿轮动载荷,并引入了齿轮动力学分析中的数学建模方法。Tian 等[10]通过建立旋转圆盘质量-弹簧-阻尼器系统模型,得到亚临界转速下圆盘前、后行波共振的失稳区域。Hotait 等[11]采用电测法分析了齿轮齿根动应力,并研究了齿根应力与动态传动误差之间的关联性。刘海鸥等[1]从弧齿锥齿轮动态响应出发,开展弧齿锥齿轮动应力分析计算及测试。
上述研究成果虽然对齿轮动应力学发展起着推动作用,但针对航空发动机中央传动齿轮振动特性分析与应力试验验证尚存在两点不足:①现有的齿轮动应力理论计算模型不能完整模拟中央传动齿轮的实际载荷和振动环境;②由于中央传动齿轮受发动机总体支点布局、压气机流道、主轴直径等结构尺寸限制,采用传统滑环引电器进行应变信号传输测试的方式,试验将面临应变计存活率较低,获取的有效数据较少,无法支撑结果分析的困境。
本文在行波共振理论的基础上,对航空发动锥齿轮进行了振动分析;采用有限元分析法计算了航空发动机中央传动从动锥齿轮行波共振的频率、共振转速以及共振裕度;并采用“轴心引线-遥测无线传输”的振动应力测试方案,实现航空发动机中央传动从动锥齿轮油污工作环境下行波共振测试,获得从动锥齿轮行波共振频率、共振转速以及不同节径行波共振时的振动应力幅值。本文形成的振动理论分析技术和试验研究方法,可为航空发动机锥齿轮振动设计和结构改型设计提供依据,具有很好的应用价值。
2 行波振动分析
2.1 危险模态识别
锥齿轮振动模态主要有节径型、节圆型和节径、节圆混合型等3种[12],如图1所示。在共振分析中要完全避开以上所有模态极其困难,这种情况就需要重点分析和避开危险模态。在工程实际中,由于齿轮动应力测试数据较少以及设计经验不足等原因,可能导致设计中为盲目避开一些非危险模态,使得真正的危险模态没有避开的情况发生。
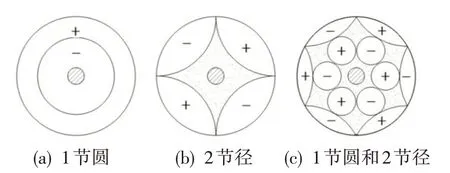
图1 齿轮振型示意图Fig.1 Sketch of gear vibration mode
根据齿轮激励能量做功对四种典型振动模态进行分析,得到齿轮危险模态如下。
振动模态一:齿轮节圆型振动。如果齿轮发生节圆型振动,则需要有沿圆周方向的交变轴向力进行激振。但是齿轮在某时刻,单个啮合齿不会周向整圈同时受力,且齿轮轴向力直接从轴承处传出。因此齿轮节圆型振动被激振力激起的可能性非常小,该型振动为非危险振动。
振动模态二:齿轮1节径型振动。当齿轮发生1节径型振动时,齿轮受到的激励力由转轴产生,具体表现为齿轮轴发生弯曲振动,其激励来源于轴系临界转速的激励。这种情况下的振动,非临界转速下,该型振动为非危险振动。
振动模态三:齿轮2 节径及以上节径型振动。当齿轮发生2 节径及以上节径型振动时,单个啮合齿单独受激振力作用,在激振力作用下易发生共振。该型振动为危险振动。
振动模态四:齿轮发生节圆节径复合型振动。齿轮在同一时刻,单个啮合齿受力不会周向整圈同时受力,单激振力很难将两种振型同时激起。因此,该型振动为非危险振动。
2.2 行波共振理论
节径或节线把圆盘面分成偶数个扇形区(图1),因此行波振动又称为扇形振动。相同扇区内的各点进行相同相位的轴向振动,相邻扇区的各点进行相反振动。当齿轮相对坐标系静止时,齿轮各点振动认为横向振动,其表达式为:
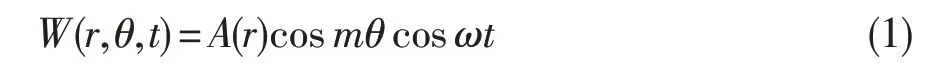
式中:W为齿轮的横向位置(mm),A(r)为振动位移最大半径处的振幅(mm),m为节径数,θ为圆周角,ω为扇形振动的角频率(rad/s),t为时间(s)。
当齿轮相对坐标系旋转运动时,公式(1)可进行三角函数展开:

由公式(2)可以得到,当齿轮受到交变力作用时,产生了左右两个行波速度相同的行波振动,如图2 所示。当旋转时这两个左右行波速度就不相同了,与旋转方向相同的为前行波,反之为后行波。
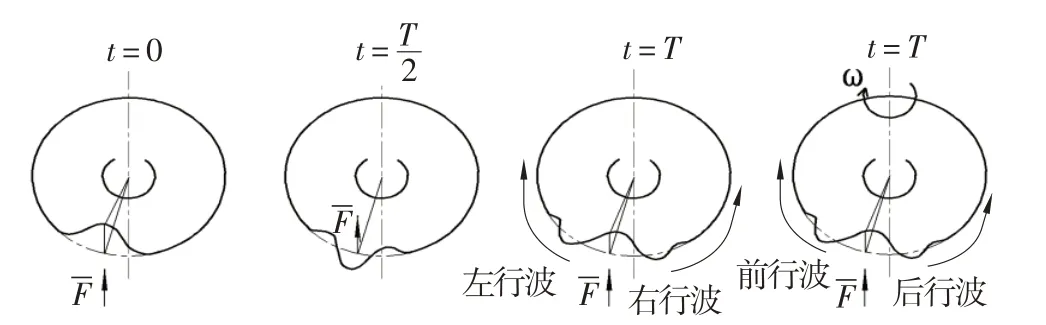
图2 行波共振原理图Fig.2 Schematic diagram of traveling wave resonance
齿轮m节径前、后行波共振表达式为:

式中:ff为齿轮前行波振动频率(Hz),fh为齿轮后行波振动频率(Hz),fd为齿轮节径型振动的动频(Hz),N为主动锥齿轮的转速(r/min),Z为齿数。
齿轮节径型行波共振发生的充分必要条件[13]:
(1) 激振力的频率和齿轮的固有振动频率属于同一坐标系。
(2) 激振力的频率等于齿轮前行波振动频率或后行波振动频率,即
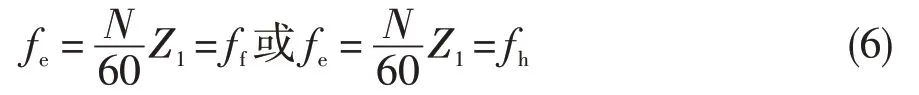
(3) 激振力对齿轮振动所做的功为正功。
将公式(6)带入式(4),可得到锥齿轮行波共振时的频率表达式为:

将公式(5)代入共公式(7),得到节径数[14]:

其中:m为正数则为后行波,m为负数则为前行波。
3 仿真计算
考虑到中央传动从动锥齿轮有35个锥齿,取整圈模型的1/35 个扇块进行计算,建立单齿齿轮扇段周期重复式的循环对称模型。扇块有限元模型见图3。约束条件为:在滚棒轴承A和滚珠轴承C处加径向约束,在B处加轴向约束,在齿轮内表面套齿连接D处选取3个点加周向约束,在循环对称面上加循环对称边界条件,计算时暂不考虑线膨胀系数。

图3 从动锥齿轮振动计算有限元模型Fig.3 Finite element model for vibration calculation of driven bevel gear
从齿轮Campbell 图可知,发动机在工作转速范围内,中央传动从动锥齿轮有多个共振点,如图4所示。图中,横坐标表示从动锥齿轮的换算转速,纵坐标表示频率(Hz),斜线为啮合激励阶次线,竖线为工作转速线,其中两条虚线表述离转速区10%的裕度线,横线为固有频率线,红点为理论计算共振点。设计转速为20 500 r/min。
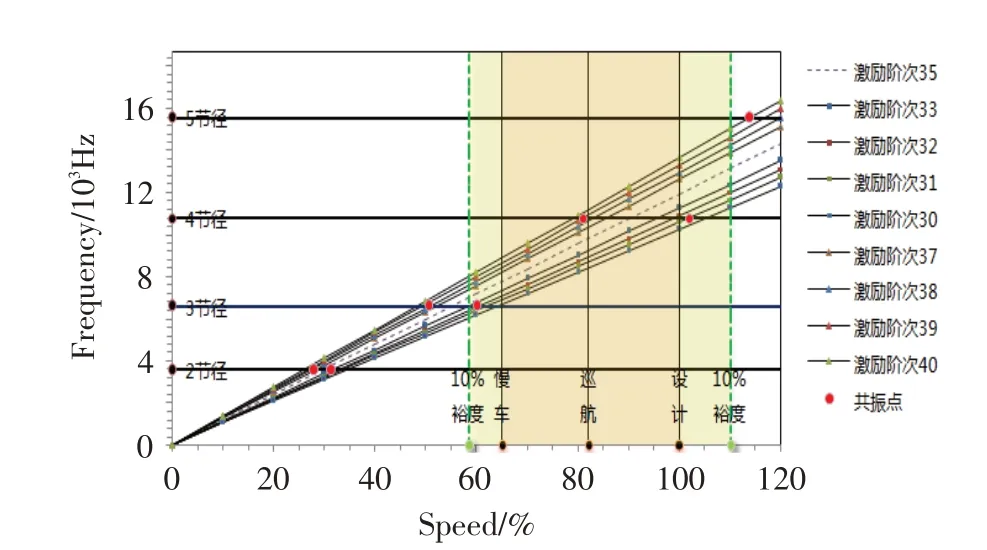
图4 行波共振转速图Fig.4 Speed diagram of traveling wave resonance
从图4 可知,该型中央传动锥齿轮主要存在2、3、4和5节径型振动,其中2节径的共振点在换算转速25%~35%之间,5节径的共振点在换算转速110%以上,3 节径后行波共振转速在换算转速45%~55%之间。3 节径前行波共振裕度和4 节径共振裕度较低,其中3节径前行波在转速13 000 r/min时发生共振,其离慢车转速裕度为-6.59%,4节径后行波在转速16 805 r/min 时发生共振,其离巡航转速裕度为-0.26%,4节径前行波在转速20 884 r/min时发生共振,其离设计转速裕度为1.91%。
仿真计算还得到,3 节径振动应力最大出现在小端齿根处,同时大端齿根、内外部辐板处,振动应力水平较高,如图5 所示;4 节径振动应力最大出现在小端齿根处,同时大端齿根、内外部辐板处,振动应力水平较高,如图6所示。

图5 3节径振动应力分布图Fig.5 3-pitch diameter distribution diagram of vibration stress
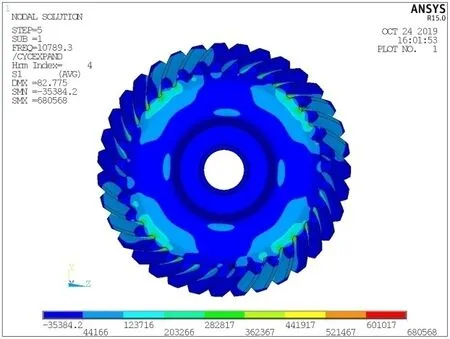
图6 4节径振动应力分布图Fig.6 4-pitch diameter distribution diagram of vibration stress
4 齿轮振动应力验证试验
为了掌握齿轮工作状态下的实际振动应力情况,同时验证齿轮振动特性的理论分析结果,在航空发动机附件传动试验台进行了齿轮工作状态下的振动应力特性试验。
4.1 试验台介绍
齿轮传动试验台主要由起动机、变速齿轮箱、中央传动系统(试验件)、柱塞泵和真实发动机附件传动系统(发附)构成,如图7 所示。其中,力加载器模拟传动系统与发动机连接的主轴承在发动机实际工作中的受力情况,柱塞泵和发动机附件加载模拟传动齿轮的功率传输情况。试验台除不能模拟发动机起动过程外,可以模拟发动机其他实际工作状态。
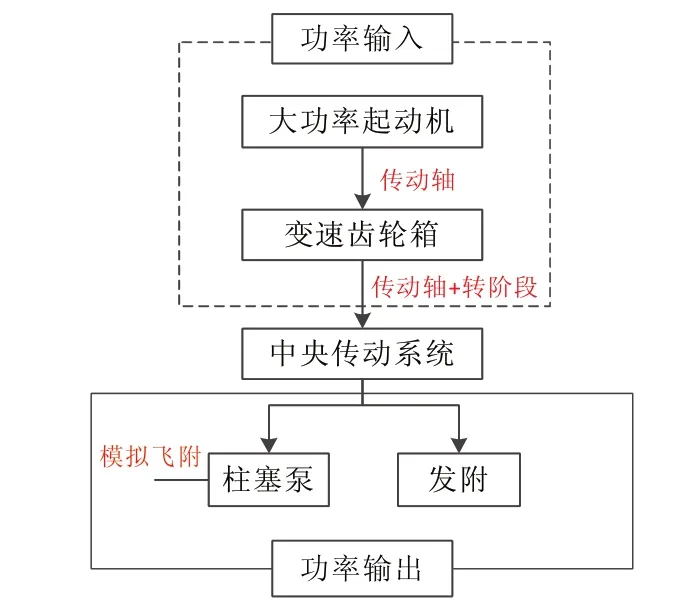
图7 齿轮传动试验台Fig.7 Test-bed of gear drive
4.2 振动应力测点设置
根据图5和图6中锥齿轮振动应力计算结果,本文根据齿轮的轮毂外侧转接圆角和内侧轮缘处接触实际面积大小,将应变计尽可能靠近边缘铺设,其中在齿根圆(凸面)铺设应变计,标记位置为Ⅰ点;在齿根圆(凹面)铺设应变计,标记位置为Ⅱ点;在辐板上铺设应变计,标记位置为Ⅲ点。Ⅰ和Ⅲ的贴片位置见图8所示的红色区域,Ⅱ在Ⅰ的背对面。

图8 应变计安装位置示意图Fig.8 Sketch of strain gauge installation location
4.3 振动应变测试
采用“轴心引线-遥测无线传输”的测试方案。在确定的振动应力测点位置,采用环氧树脂胶粘贴工艺进行应变片安装,在应变计栅丝末端进行引脚与引线焊接,引线沿设计路径间隔性点焊固定,引线与遥测信号传输发射模块相连,即应变计信号输入到遥测传输装置的发射机。信号在发射机中经放大、载频、调理、发射等处理后转变成数字信号,并通过天线发送给遥测接收机。再通过数据采集系统对振动应变信号进行采集。同时本文还采用磁电式转速传感器对试验件转速进行了测量。测试原理图如图9所示。
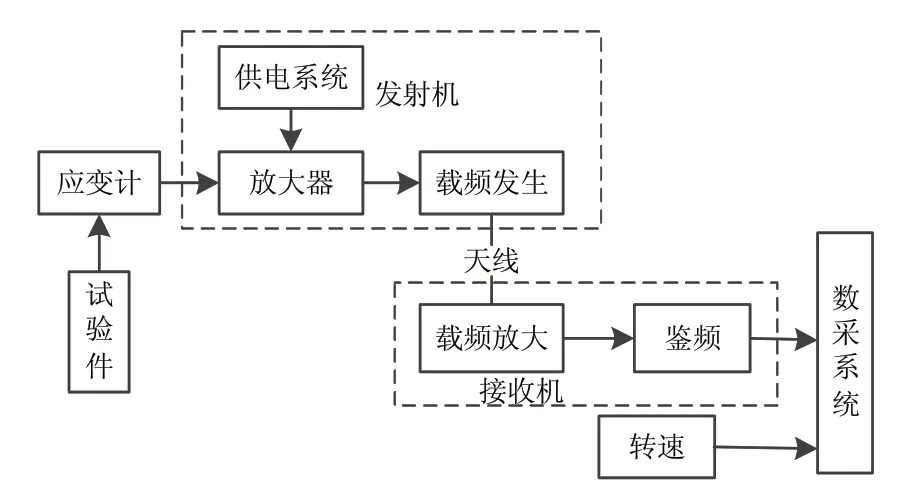
图9 振动应变测试原理框图Fig.9 Schematic diagram of vibration strain test
4.4 振动应变测试结果与分析
为模拟中央传动系统在发动机运行中的真实振动情况,试验件从0转速到1.0设计转速(20 500 r/min)进行10 min 匀速升速扫频试验。试验件的从动齿轮齿数为35。
图10 为试验过程中齿轮Ⅰ、Ⅱ和Ⅲ位置,应变计测点获取的振动应变阶次瀑布图。图中X轴为无量纲化的从动轴激励阶次,Y轴为应变幅值,Z轴为中央传动轴转速。可观察到齿轮在工作转速范围内存在固有频率与主轴激励阶次重合,出现幅值突增,表明发生齿轮共振,见图中红圈标记位置。对图中Ⅰ位置、红圈2 时刻的齿轮振动应变进行细化分析,可得到图11 所示的齿轮振动应变阶次剖面图。其中,右上图为齿轮振动应变阶次瀑布图,左上图是光标所示激励阶次(K=38)下齿轮振动应变幅值随转速变化趋势图,右下图为光标所示转速时刻(11 010 r/min)齿轮振动应变阶次谱,左下图为光标所示频率(6 957 Hz)下齿轮振动应变幅值随转速变化趋势图。
因为齿轮的齿数为35,根据公式(1)得到图11光标时刻的节径数为3,即主轴38 阶激励激起了齿轮的3 节径后行波共振。通过对图10 中其他共振点进行同样剖面图计算分析,得到表1 所示的试验结果。
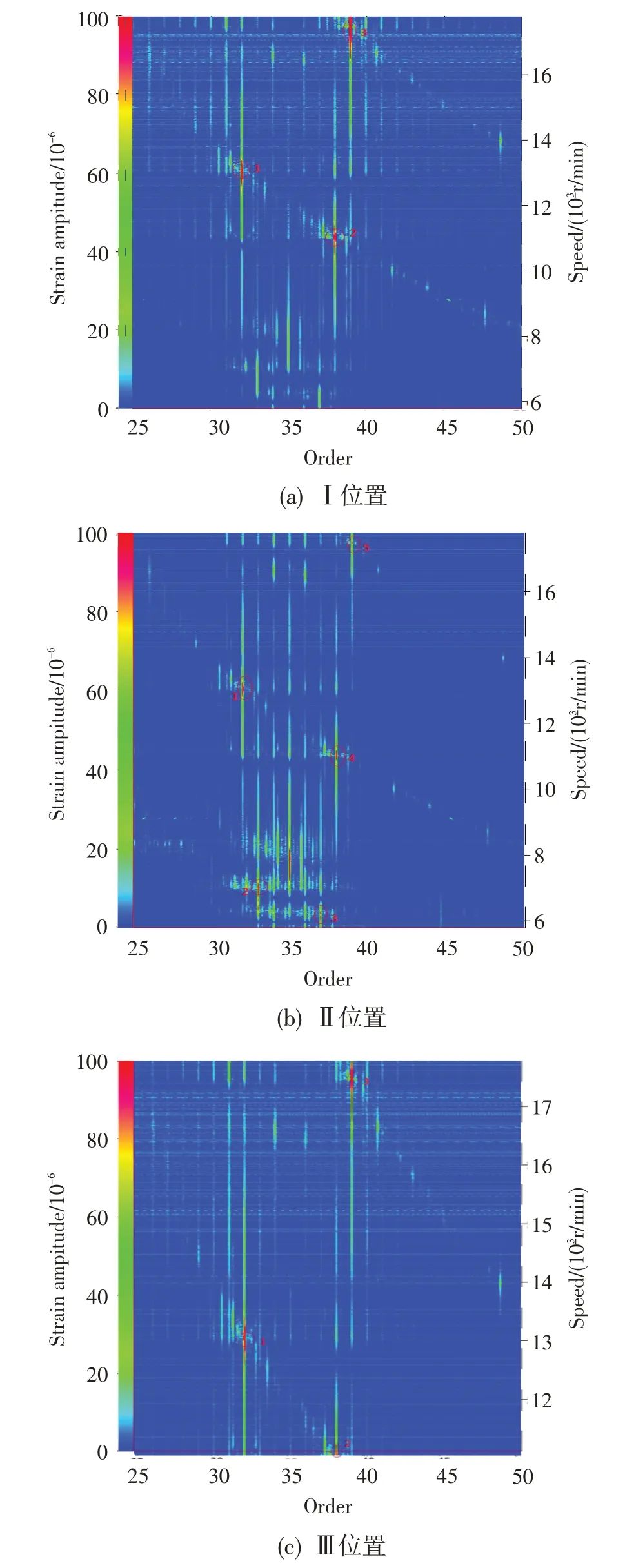
图10 齿轮动应力测点应变阶次瀑布图Fig.10 Order waterfall chart of gear vibration strain

图11 齿轮振动应变阶次细化瀑布图Fig.11 Detailed order waterfall chart of gear vibration strain
由图10和表1综合分析发现,该型发动机中央传动系统在0转速到1.0设计转速范围内,从动锥齿轮激起了明显的2节径前、后行波共振,3节径前、后行波共振和4 节径后行波共振。2 节径前行波的共振转速为6 988 r/min,即为换算转速34%;2 节径后行波的共振转速为6 250 r/min,即为换算转速30%;与理论计算的2 节径共振转速区间相吻合。3 节径前行波的共振转速为13 070 r/min,与理论计算的13 000 r/min 非常接近;3 节径后行波的共振转速为11 010 r/min,即为换算转速53.7%,与理论计算也相符合。4 节径后行波的共振转速为17 470 r/min,与理论计算的转速16 805 r/min 的误差为3.8%,具有高度的符合性。3 节径前行波和4 节径后行波激起的共振在工作转速范围,其中3 节径前行波共振最大振动应变幅值为257.5×10-6,应力51.5 MPa,4节径后行波共振最大振动应变幅值为472.7×10-6,应力为94.5 MPa,将4 节径后行波共振幅值换算到最大振动力区,其幅值为323 MPa。参考文献[14]中规定齿轮动应力不应超过100 MPa,从而判定齿轮振动存在风险,进一步对比Goodman图可知,此时齿轮的强度储备系数不足,超过设计许用应力,说明齿轮在工作中可能存在风险。上述分析表明,该型发动机的中央传动齿轮在工作转速区间共振应力较大,需要对齿轮开展减振设计。
5 结论
在行波共振理论分析的基础上,采用数值仿真计算与试验验证相结合的方式,研究了航空发动机中央传动从动锥齿轮的振动特性,得到如下结论:
(1) 行波共振分析的危险模态与试验验证结果具有高度吻合性,理论分析结果说明了试验结果的有效性,试验结果验证了理论分析和数值计算方法的可行性。文中的振动分析方法可以推广应用到航空发动机所有锥齿轮的振动设计和结构改型设计中,振动应力测试方法可用于发动机其他部件振动应力测试借鉴。
(2) 该型航空发动机中央传动从动锥齿轮,在设计转速范围内存在2节径前后行波、3节径前后行波共振和4 节径后行波共振。3 节径前行波和4 节径后行波激起的共振转速落在工作转速范围内,最大共振应变幅值为472.7×10-6,换算后该从动锥齿轮的最大振动应力达到323 MPa,超过设计许用应力,齿轮存在振动风险。为提高该型发动机中央传动从动锥齿轮的安全性,需对其进行齿轮结构改型或减振设计,使其在工作转速范围内的3节径和4节径共振应力幅值减小,或避开3节径和4节径行波振动危险转速。

