涡轮榫连接结构抗微动疲劳损伤优化设计

严小冬，张宏建，邢泽宇，于子强，崔海涛，温卫东

(南京航空航天大学能源与动力学院，南京 210016)

1 引言

微动是指相互接触的表面之间存在的振幅极小(微米量级)的运动。在振动环境下，两个紧密配合的表面极易产生微动[1]。微动按照损伤形式可以分为微动疲劳、微动磨损和微动腐蚀三大类。工程中，微动疲劳是连接结构失效的主要模式之一，其引起后果的严重性也往往超过微动腐蚀与磨损[2]，因此微动疲劳又被称为工业癌症。

在飞机和航空发动机中，有很多零部件的连接结构(如各种榫连接结构、铆钉连接结构等)都存在着微动疲劳，这将显著降低零件的使用寿命。飞机故障中，因航空发动机榫连接结构的微动疲劳失效而造成的占主要部分[3]。因此，对榫连接结构进行优化设计从而延长其微动疲劳寿命是十分迫切的需求。国内外学者针对航空发动机榫连接结构的应力分析[4-8]与优化设计开展了大量的研究。Song等[9]在进行涡轮榫齿结构的形状优化时，提出用样条曲线来实现接触区过渡的方案，实现了应力的改善以及疲劳寿命的提升，但这种设计大大增加了制造难度。陈开军等[10]针对航空发动机中大量存在的枞树形榫连接结构，对其形状尺寸进行了优化设计，获得了满足要求的二齿榫连接结构尺寸。邢誉峰等[11]针对发动机涡轮盘枞树形榫槽结构，选择26个形状控制变量，为优化设计变量，以减小最大应力为目标进行优化设计，降低了榫槽结构的应力梯度，提升了结构的使用寿命。杨敏超等[12]以榫连接结构第一主应力和最大等效应力的加权值为目标函数，对三齿枞树形榫连接结构进行了尺寸优化。申秀丽等[13]运用梯度法对三齿枞树形榫头/榫槽结构进行灵敏度分析，以主要结构参数为设计变量，以最大等效应力极小化作为目标函数，提出了详细的形状优化设计方法。谢筱庆[14]提出将齿间过渡和榫齿接触的单圆弧设计改为双圆弧设计的思想，并以此为基础建立了二齿、三齿榫连接结构优化设计模型和方法。

综上所述，目前的航空发动机榫连接结构优化设计方法，通常以降低结构的最大等效应力、减小应力集中为目标，没有考虑微动损伤的影响。由于榫连接结构的微动疲劳处于一种极其复杂的应力状态，影响其寿命的因素众多，因此只考虑应力大小是不够的。本文以某型涡轮榫连接结构上齿模拟件为研究对象，对其形状尺寸进行分析，确定了影响微动疲劳寿命的主要参数；以确定的参数为设计变量，以微动疲劳寿命为目标函数，建立了榫连接结构抗微动疲劳损伤的优化设计方法。研究成果为涡轮榫连接结构的设计提供了参考，具有一定的理论和工程实用价值。

2 榫连接结构参数化有限元模型

榫连接结构的参数化，是其抗微动疲劳损伤优化设计的前提和基础。设计参数越多，榫连接结构可变性越大，优化计算工作量也成倍增加。因此，为提高优化效率，通常要求用较少的设计参数确定出定性合理的榫连接结构[15]。相对于枞树形两齿或三齿结构，单齿模型结构更加简单，设计参数较少，分析计算也更快捷，优化效率更高。本文通过模拟真实涡轮榫连接结构接触区域的最大等效应力和相对滑移幅值，建立榫连接结构单齿有限元模型，图1给出了描述单齿结构所需的12 个独立参数。图中，Wedge_angle表示榫头榫槽的顶角，Chamfer_angle表示榫齿倾角，H表示榫头高度，H3表示榫头齿高，H1表示榫头接触中心至榫头颈部的高度，W1表示接触中心位置宽度，R_r1和R_r2表示榫头齿间过渡圆弧半径，R_r3表示榫头底面过渡圆弧半径，h表示榫头底面与榫槽底面间隙，G_r0表示榫槽顶面过渡圆弧半径，G_r1表示榫槽齿间过渡圆弧半径。

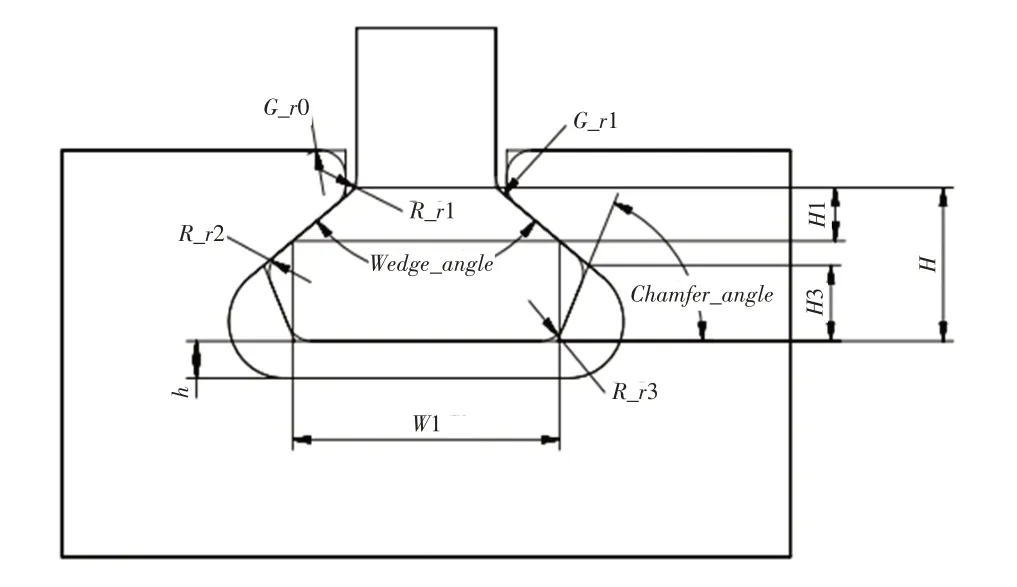
图1 榫连接结构几何参数Fig.1 Geometric parameters of dovetail structure

因榫连接结构的对称性，故只建立1/2 有限元模型，以进一步提高计算效率。有限元模型如图2所示。榫头和榫槽的材料均为高温合金ZSGH4169，其密度为8 240 kg/m3。单元类型选择平面8节点单元PLANE82，整体网格尺寸为0.5 mm，且在榫头与榫槽的接触区及其附近进行网格加密以提高计算精度。

图2 榫连接结构有限元模型Fig.2 Finite element model of dovetail structure

3 灵敏度分析

对榫连接结构进行优化时，不需把所有尺寸参数都重新设计，只需对参数进行灵敏度分析，选出对目标函数影响最大的参数作为设计参数进行优化。以ISIGHT 软件为平台，在其试验设计(DOE)模块中实现结构参数的灵敏度分析。试验设计模块里的因子(Factors)是输入变量即为设计参数，响应(Response)是输出变量即为目标函数。针对本文，响应是微动疲劳寿命。

试验设计方法有多种，本文选择的是参数试验(Parameter study)方法。此方法在保持其他参数为基值的情况下单独研究某个参数的敏感性，虽不能研究各参数之间的相互影响，但可在多个水平上研究多个参数，只需对较少的设计点进行评估。图3 显示了三因子的参数试验样本点。

图3 三因子参数试验方法示意图Fig.3 Schematic diagram of parameter study method

图4为榫连接结构参数的Pareto图，反映了样本拟合后模型中所有项对每个响应的贡献程度百分比。本文以Pareto图来判断各参数对于微动疲劳寿命的灵敏度。图中蓝条表示正效应，红条表示反效应。可看出参数H和Wedge_angle对微动疲劳寿命的影响最显著。综合考虑各参数的灵敏度和优化计算量，选取对微动疲劳寿命影响最大的前5个参数，即H、Wedge_angle、H3、R_r2和G_r1，作为榫连接结构优化设计的设计变量。

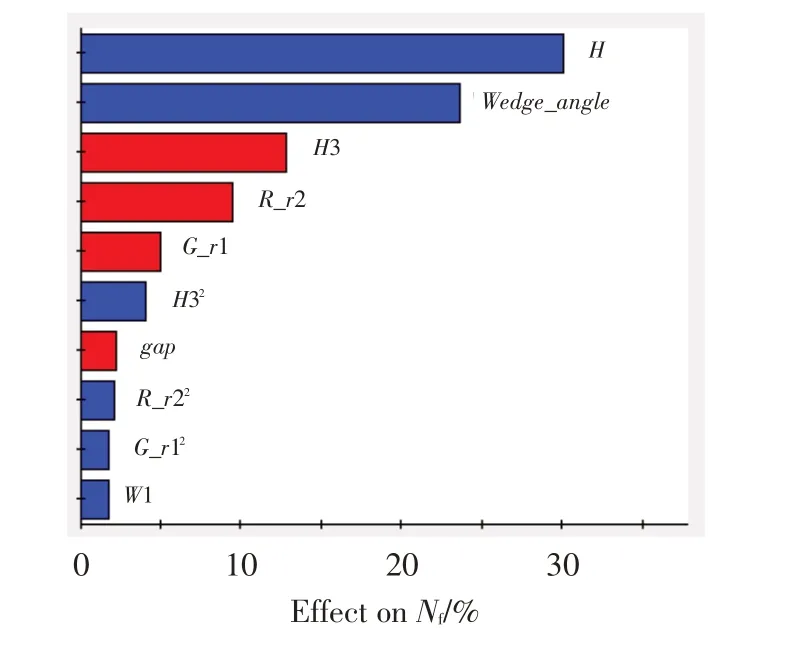
图4 榫连接结构参数的Pareto图Fig.4 Pareto diagram of dovetail structure

4 榫连接结构优化设计

4.1 优化问题描述

(1) 设计参数与目标函数

设计参数为灵敏度分析后选出的5 个参数，目标函数则为微动疲劳寿命。

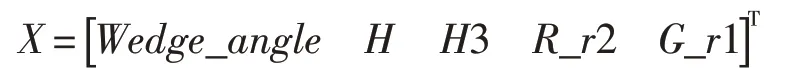
(2) 约束条件

约束条件包括几何约束和强度约束。其中几何约束为保证模型形状正确时的设计参数取值范围；强度约束为最大拉应力、最大等效应力、最大剪应力、最大挤压应力均不超过其许用值。

(3) 优化数学模型

涡轮榫连接结构抗微动疲劳损伤优化设计问题可以用以下数学模型描述。

式中：N为目标函数，即微动疲劳寿命；X为设计变量；gi为约束条件。

4.2 优化过程

基于多学科优化平台ISIGHT编写批处理文件，集成ANSYS和MATLAB，完成对涡轮榫连接结构的优化设计。具体步骤为：在ANSYS中输入设计参数建立榫连接结构参数化模型并进行接触分析，提取接触区各节点的应力应变数据生成输出文件；将输出文件导入MATLAB计算微动疲劳寿命；由ISIGHT中的优化模块判断约束条件是否满足以及目标函数是否最优。以上步骤均在ISIGHT软件中自动完成，优化流程如图5所示。

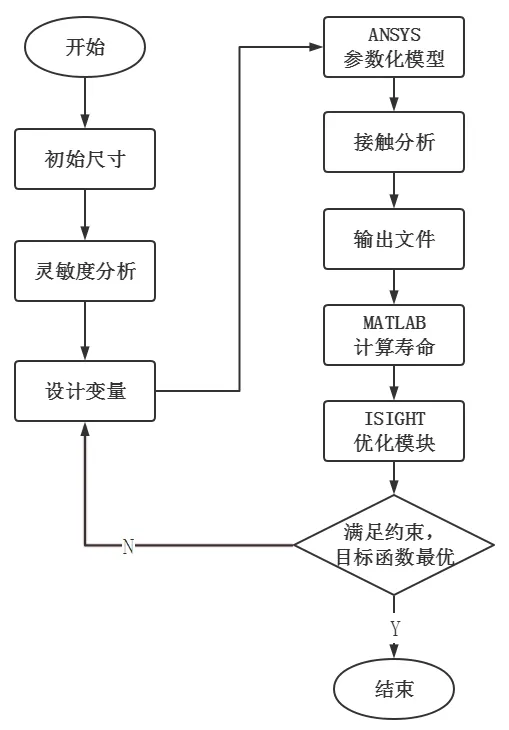
图5 榫连接结构优化设计流程Fig.5 Optimized design process of dovetail structure

4.3 优化结果及分析

分别采用序列二次规划算法(NLPQL)和多岛遗传算法(MIGA)，对涡轮榫连接结构进行优化设计。其中多岛遗传算法中的子群规模为5，岛的个数为3，总共进化的代数为8，即总迭代次数为120次。

优化前后设计参数值见表1和表2。由表可知：优化后参数Wedge_angle和H变大，参数H3、R_r2和G_r1变小，这与灵敏度分析后的Pareto图中显示的参数与微动疲劳寿命之间的关系一致。

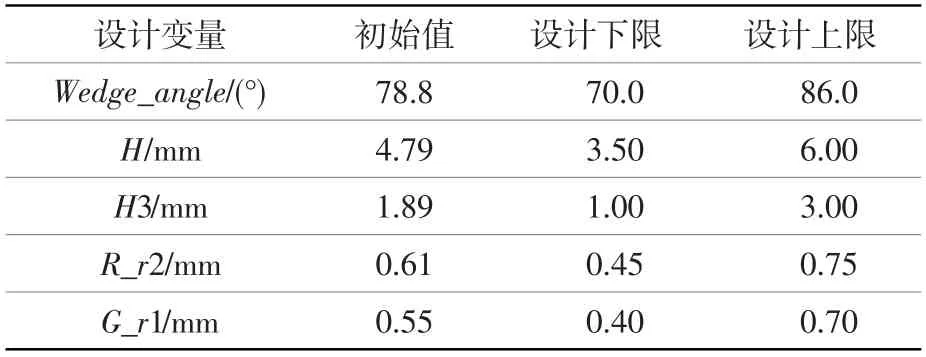
表1 设计参数的初始值和取值范围Table 1 Initial values and value ranges of design variables

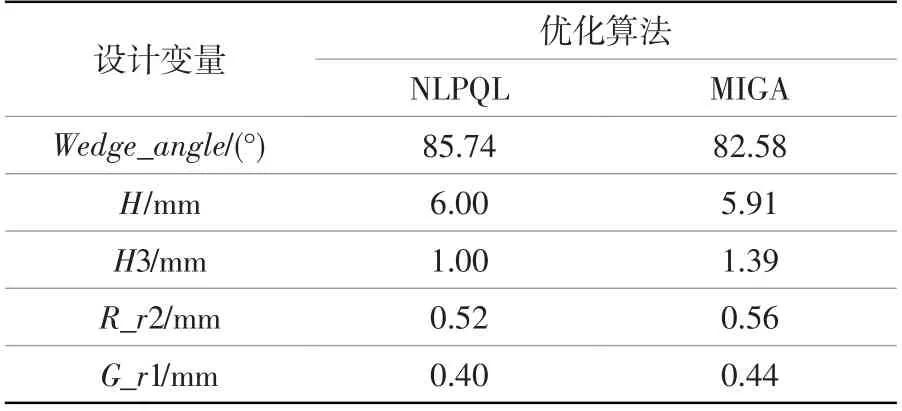
表2 优化后设计参数的值Table 2 Value of design variables after optimization

图6 为两种优化算法目标函数的迭代情况，其横坐标为优化迭代次数，纵坐标为目标函数，即微动疲劳寿命。可看出：优化前结构的微动疲劳寿命为53 404次循环，优化算法NLPQL、MIGA分别让微动疲劳寿命提升到了843 542 次循环和537 485 次循环。两种优化方法都极大地延长了结构的微动疲劳寿命；相比MIGA算法，NLPQL算法以更少的迭代次数(61次)得到了更好的优化结果。因此涡轮榫连接结构的优化设计采用NLPQL算法效率更高。

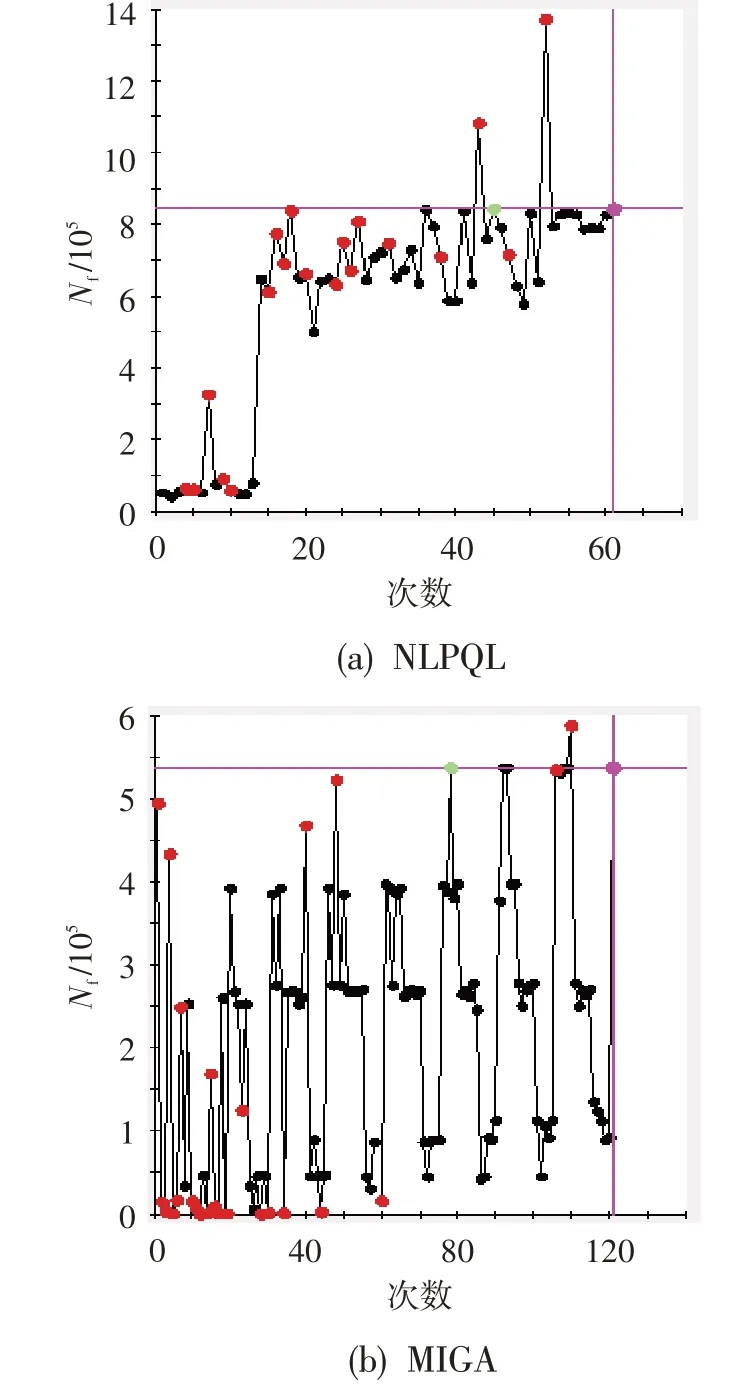
图6 目标函数迭代情况Fig.6 Iteration of the objective function

图7、图8 分别为NLPQL 算法优化前后榫连接结构的等效应力云图和接触压力云图。可见，优化后结构的应力分布更均匀，且最大等效应力以及最大接触压力都得到了有效降低。图中等效应力和接触压力最大点均出现在接触区边缘，这与微动疲劳试验中裂纹最先萌生的位置吻合。

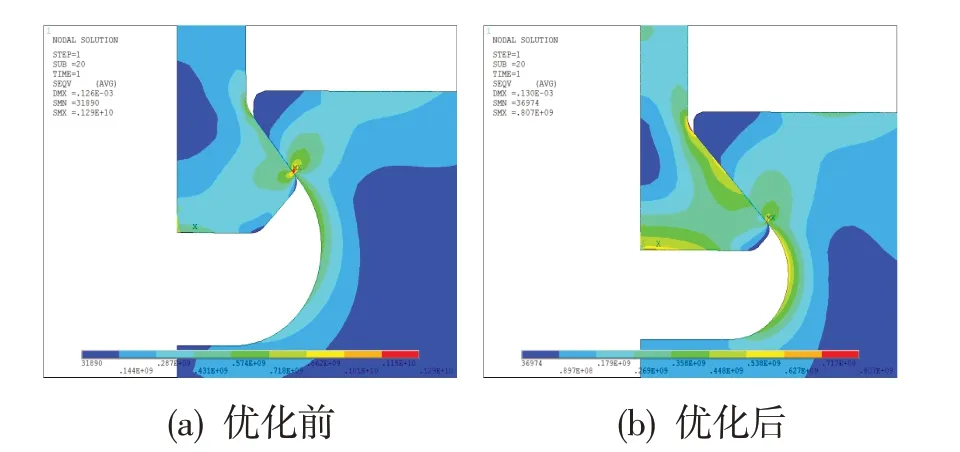
图7 NLPQL算法优化前后等效应力云图Fig.7 Von-Mises stress cloud before and after NLPQL optimization

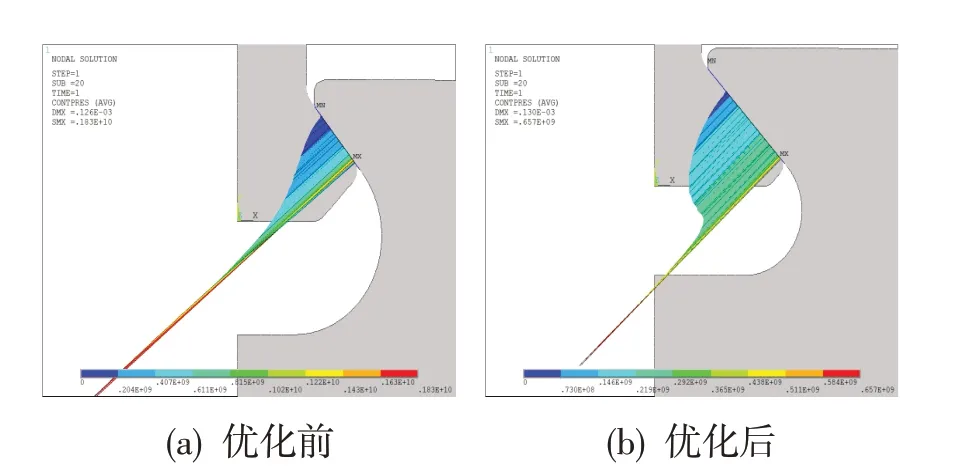
图8 NLPQL算法优化前后接触压力云图Fig.8 Contact pressure cloud before and after NLPQL optimization

5 微动疲劳寿命试验验证

为验证优化设计的可靠性，开展了NLPQL算法优化后榫连接结构的微动疲劳寿命试验。试验装置和试验件见图9。微动疲劳寿命试验在650℃高温下进行，轴向载荷峰值分别为14 kN 和17 kN，载荷比0.1，频率为10 Hz。试验结果见表3，表中每个工况的寿命均为3 件试验件的寿命平均值。可见，通过优化提高了榫连接结构的微动疲劳寿命，其中轴向载荷为14 kN 时寿命提高了62.24%，轴向载荷为17 kN 时寿命提高了13.55%。试验结果证明，所提出的优化设计合理有效。

图9 试验装置及试验件Fig.9 Testing device and test piece

表3 微动疲劳寿命试验结果Table 3 Fretting fatigue life test results

6 结论

以某型涡轮榫连接结构上齿模拟件为研究对象，建立了其参数化有限元模型；利用参数试验的方法，对榫连接结构特征参数进行灵敏度分析，确定了影响结构微动疲劳寿命的主要参数；基于多学科优化平台ISIGHT，以主要特征参数为设计参数，以微动疲劳寿命为目标函数，分别采用序列二次规划算法和多岛遗传算法完成了对榫连接结构的优化设计，得到如下结论：

(1) 序列二次规划算法比多岛遗传算法优化效果更好，优化效率更高。

(2) 通过优化提高了榫连接结构的微动疲劳寿命，同时有效降低了结构的最大等效应力和最大接触压力，改善了结构的应力分布。

(3) 试验验证了优化设计的有效性，优化结果对涡轮榫连接结构的设计具有一定的参考价值。