基于差分进化算法的航空发动机仿真模型修正方法

曹铭栋，樊 巍，刘 兵，陈宣亮，王孝军

(中国航发四川燃气涡轮研究院，成都 610500)

1 引言

航空发动机作为一种复杂的热机系统，研发过程中离不开整机仿真和整机试验。目前，整机稳态性能仿真主要采用基于部件级模型构建的变比热整机仿真模型[1-6]，其基本原理是基于各个部件的试验或仿真特性，在整机稳态模型中利用Newton-Raphson 等方法，求解流量平衡、功率平衡等共同工作方程，获取各个部件在整机中的共同工作点。但是在实际工程中，各个部件受到结构上的加工与装配偏差、使用过程中的性能退化、整机高温/高压恶劣的工作环境等因素影响，使各部件在整机环境下的实际工作特性，与单个部件试验特性存在差异。此外，整机仿真模型中采用了较多理想建模假设[7]，从而造成整机仿真结果与整机试验结果存在一定的偏差，无法准确指导发动机优化设计。

现阶段针对航空发动机仿真模型的修正方法，主要有基于最小二乘法对误差函数进行求解，获取修正系数的方法[8]，以及基于现代优化算法的仿真模型修正方法。基于最小二乘法对误差函数进行求解，获取修正系数的方法，必须要发动机测量参数数目大于等于修正参数数目，但实际情况中，发动机上的测量参数数目往往小于修正参数数目。基于现代优化算法的仿真模型修正方法，将测量参数与仿真参数之间的偏差函数，转化为使偏差量最小的优化问题，不受测量参数数目必须大于等于修正参数数目的限制。因此，基于现代优化算法的仿真模型修正方法，在仿真模型修正中得到了较多运用[9-13]。现代优化算法主要有遗传算法、蚁群算法、粒子群算法、文化算法和模拟退火法等，这些算法无需知道优化模型的具体函数解析式，以及优化变量是否连续，其基本思想是，从初始点开始利用相应算法的状态转移规则，在合理的概率状态规则下搜索更优点[14]。然而，现代优化算法计算量较大，收敛速度相对较慢，且在求解多维优化问题时，容易陷入局部最优，降低了仿真模型修正效率和修正精度。因此，寻找一种基于高效优化算法的仿真模型修正方法，已经成为整机仿真模型修正的一个重要研究方向。本文将仿真模型修正问题，转化为求取测量与仿真之间偏差函数的最优化问题，进一步采用优化精度较高的三次变异差分进化算法作为仿真修正算法，通过该算法在仿真模型修正上的运用，以提高仿真修正的精度与效率，可满足工程实际运用需求。

2 仿真修正建模

假设发动机有m个测量参数Qm，而此时在仿真模型中，各个测量参数对应的仿真模型计算值为Om，则每个测量参数的偏差量em可以表示为：

对于整个发动机的测量参数与对应参数仿真结果的偏差量，可以用偏差加权函数F(X)表示为：

式中：ai为第i个测量参数的加权因子，CFi为引入的n个部件修正量中的第i个修正量。

仿真修正的目标是，使发动机各试验测量参数与对应参数仿真结果的偏差量尽可能小，即偏差加权函数F(CF1,CF2,…,CFn)最小。由此可将F(CF1,CF2,…,CFn)最小值的求取转化为最小值优化问题，如下式所示：

式中：CFj,min和CFj,max分别为对应修正量的上限值与下限值。

由此建立如图1所示的仿真模型修正流程。首先，由优化算法根据各个部件修正量的上、下限，自动生成各个部件的修正量，并对部件特性进行对应修正，修正完成后带入到仿真模型中进行计算，获取仿真模型计算值；其次，将仿真模型计算值与试验测量参数按照式(2)计算，得到偏差加权函数；最后，判断此时的偏差加权函数是否小于要求精度，小于要求精度则完成修正，不小于要求精度，则由优化算法按照获取最小偏差加权函数为目标，生成新的部件修正量，并重复以上步骤。

图1 仿真模型修正流程Fig.1 Process of simulation model modification

3 优化算法

3.1 差分进化算法

由仿真模型修正流程可知，发动机仿真模型修正是一个多约束条件、多维度且无具体函数表达式的最小值优化问题，选择一种高效的优化算法，是整个仿真模型修正的关键步骤。相较于经典优化算法，现代优化算法更适合发动机仿真模型修正。而在现代优化算法中，差分进化算法的结构相对简单、调整参数少，相比其他现代优化算法具有更高的计算精度和鲁棒性[15]，为此在航空发动机设计领域得到了广泛运用[14，16-18]。经典的现代差分进化算法结构如图2所示，包含了种群初始化、变异、交叉、选择等操作。其中，算法中的个体适应度计算(适应度函数计算)即为偏差加权函数计算，终止条件的判断即为偏差函数结果是否满足修正设置精度要求。

图2 经典差分进化算法流程图Fig.2 Process of typical differential evolution algorithm

种群初始化按式(4)的方法进行：

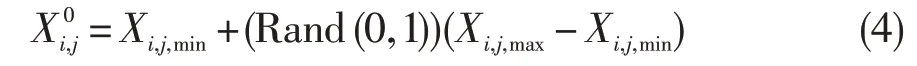
变异操作按式(5)的方法进行：

3.2 算法改进与测试

为了进一步提升差分进化算法的全局收敛性和计算前效率，采用作者在经典差分进化算法的基础上，基于种群熵的种群初始化策略、精英保留策略、动态调整变异策略、交叉概率自适应等措施进行改进，提出的自适应三次变异差分进化算法[14，16]。其算法结构如图3所示，与经典差分进化算法基本一致。

图3 自适应三次变异差分进化算法流程图Fig.3 Process of self-adaptive three times variation differential evolution algorithm

自适应三次变异差分进化算法采用基于种群熵的种群初始化策略，使优化变量初始化更加均匀，提高了初始种群变量的多样性，有利于在整个空间中搜索全局最优解。精英保留策略使当前种群的最优个体能尽可能地被保留到下一代，加快算法收敛速度。动态调整变异策略增加了优化过程中的种群多样性，使算法在优化过程中的搜索能力增强。交叉概率自适应使算法在前期拥有较高的全局搜索能力，在后期拥有较高的局部搜索能力，以提升计算精度，以此动态平衡算法搜索能力和计算精度。种群初始化策略、精英保留策略、动态调整变异策略、交叉概率自适应的具体算法可参考文献[14]和[16]。

4 算例分析

4.1 试验测试布局

为了验证仿真模型修正的可行性，基于某型双转子混合排气涡扇发动机实际试验参数对仿真模型进行修正。该型发动机的构型如图4 所示，其测量参数如表1所示。

图4 发动机构型示意图Fig.4 Diagram of engine configuration

表1 发动机试验测量参数Table 1 Engine test measurement parameters

获得整机相关测量参数后，通过基于流量平衡、功率平衡的试验分析方法[5]，可进一步获取整机试验条件下，各个部件的性能参数和燃烧室出口总温等参数。

4.2 仿真模型偏差分析

基于差分进化算法的仿真模型修正，需要给定修正量的上限值和下限值，即修正量的取值范围。修正量取值范围不合理，将会导致算法无法捕获合适的修正量，导致仿真模型修正失败。因此，修正前需对试验测量参数与仿真模型所计算得到的参数进行偏差分析，进而获取各个修正量的取值范围。表2给出了修正前整机仿真模型计算得到的部件性能参数、推力和耗油率等总体性能参数，与试验条件下对应参数的对比情况。可以看出，虽然未修正前仿真结果的推力和耗油率与试验值偏差不大，但各部件试验参数与仿真结果偏差较大。由此可以表明，整机试验参数——推力、耗油率与仿真结果基本相当的条件下，并不能代表各部件参数的仿真结果与实际试验参数的一致。因此，仿真模型的修正对于指导后续发动机的设计与评估分析尤为重要。

表2 仿真模型参数与试验数据对比Table 2 Comparison of simulation model parameters and test parameters

在对仿真模型进行修正时，主要是对部件的特性进行修正。因此，修正参数主要为压缩部件、涡轮部件的进口换算流量和效率。对于混合排气发动机，混合器外涵进口面积的变化也会影响到整机匹配，而整机实际工作中混合器内外涵气动面积与实际物理面积存在一定差异，因此考虑将混合器外涵进口面积也作为仿真模型修正参数。基于以上考虑，并结合仿真模型与实际试验的偏差分析结果，可获取相关修正参数及其取值范围，如表3所示。

表3 仿真模型修正参数选取与取值范围Table 3 Modification parameter selection and value range of simulation model

4.3 仿真修正

在选定仿真修正参数后，还需要选择试验目标参数，通过对比修正后的仿真计算参数与试验目标参数，判断模型修正是否完成。目标参数除整机测量的推力和耗油率外，还应包括各个部件在整机中的匹配工作点。由于部件修正中已选取流量修正量与效率修正量，压比、膨胀比、燃烧室出口总温为匹配计算结果，因此可将压缩部件的压比、涡轮部件的膨胀比和燃烧室出口总温增加为目标量。对于本算例中的双转子混合排气涡扇发动机，其控制规律为双转速控制，实际控制中，主要是通过控制高压相对物理转速和喷管喉部面积实现，所以还需要将喷管喉部面积增加为目标量。基于以上分析可知，仿真修正的目标量与表2所列参数一致。图5为仿真与试验偏差加权函数随优化迭代次数的变化。从图中可知，随着迭代次数的增加，偏差加权函数值不断降低，当迭代至600次时，偏差加权函数值小于设定值(0.005)。

图5 偏差加权函数随迭代次数的变化Fig.5 Deviation weighting function with the times of loop iteration

表4给出了最终的模型修正量的修正值。从表可以看出，整机环境下，发动机各部件的加工偏差、各部件进口条件变化等，都会使实际部件的工作参数与仿真参数有差异。特别是混合器外涵面积，其修正量较给定的物理面积偏大约40.78%，表明整机环境下由于内外涵气流相互作用，混合器的气动面积与实际物理面积有较大差异。而该参数将直接影响风扇工作线的位置，因此在仿真修正与整机匹配设计中要予以特别关注。

表4 仿真模型修正量取值Table 4 Value of simulation model modification parameters

表5和图6给出了修正前后仿真模型参数与试验参数偏差量的对比情况。图6 中，红色代表修正前偏差，蓝色代表修正后偏差。可见，修正后的仿真模型在整机性能参数、各部件参数上，较修正前的偏差值明显减小。相关仿真模型参数与试验参数的偏差均小于1.0%，满足仿真模型修正需求。

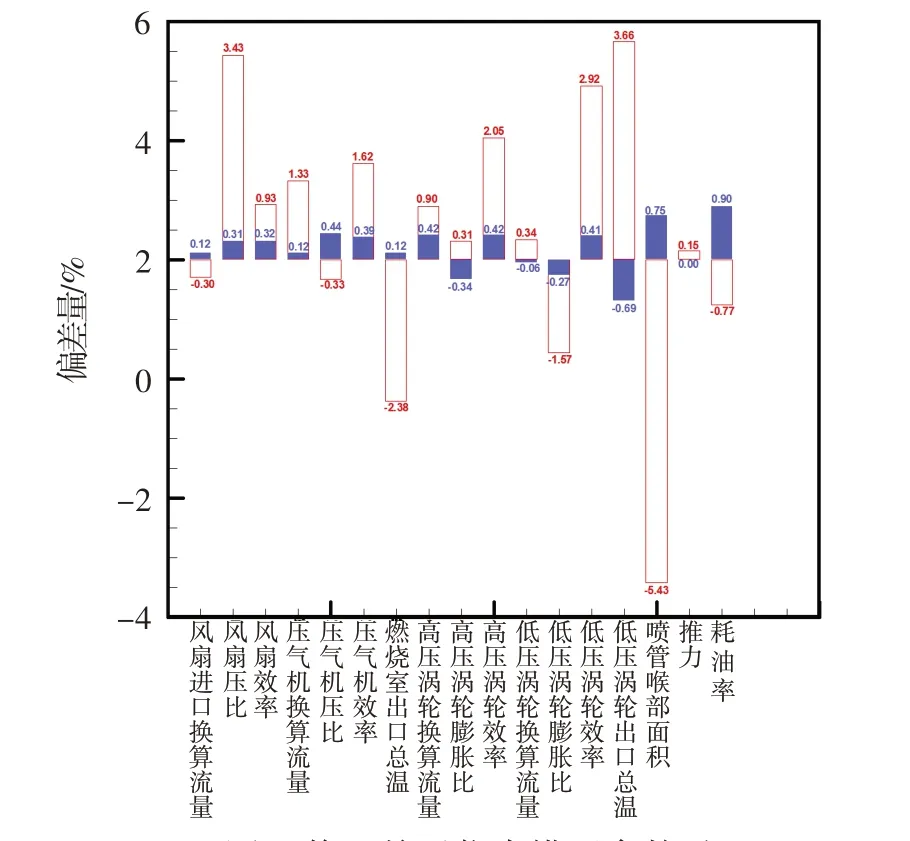
图6 修正前后仿真模型参数对比Fig.6 Comparison of simulation model parameters and test parameters before and after modification

表5 修正前后仿真模型参数与试验参数对比Table 5 Comparison of simulation model parameters and test parameters before and after modification

5 结论

针对航空发动机仿真模型修正问题，采用自适应三次变异差分进化算法，将仿真模型修正转化为求取测量与仿真之间偏差函数的最优化问题。利用以上方法，基于某型双轴混排涡扇发动机试验数据开展了仿真模型修正研究，得到如下结论：

(1) 修正后的仿真模型参数与试验参数的偏差减小至1.0%以内，可以有效地解决该类模型的修正问题，满足工程实际运用需求。后续可以进一步开展算法优化、修正精度提升等研究，降低偏差，将校核修正精度提升至0.5%左右。

(2) 在整机试验参数推力、耗油率与仿真结果基本相当的条件下，各部件参数的仿真结果与实际试验参数可能存在不一致的情况，需要基于试验数据对仿真模型进行修正，以指导后续发动机的设计与评估分析。

(3) 在整机环境下，由于混合器内外涵气流相互作用，混合器气动面积与实际物理面积有较大差异，在仿真修正与整机匹配设计中要予以特别关注。