倍窗口相参扩频序列估计算法*

李 星，魏 勋，张利强，盛 兴，候鑫珏

(1.光电对抗测试评估技术重点实验室，河南 洛阳 410073；2.中国人民解放军 96862部队,河南 洛阳 410073)

0 引 言

直接序列扩展频谱(Direct Sequence Spread Spectrum，DSSS)通信简称直扩通信，是一种常用的通信方式，具有较强的抗截获和抗干扰性能，广泛应用在各种军用通信系统中。由于直扩通信信号信噪比较低，经常淹没在噪声之中，难以对直扩通信系统实施有效的侦察与干扰。在直扩通信系统中，扩频序列是最重要的特征，在非协作通信环境下，获取扩频序列能够对直扩通信信号进行解调，在对抗中获取扩频序列能够对直扩通信系统进行高效的相关干扰[1-2]，因此扩频序列盲估计是直扩通信对抗的重要内容。

Burel等[3]首次提出特征分解扩频序列估计算法，通过对直扩信号的协方差矩阵进行特征分解，然后拼接主、次特征向量，得到扩频序列，但该算法存在相位模糊问题。为了解决这个问题，他又在文献[4]中提出了首先对直扩信号进行同步，然后通过特征分解算法估计扩频码序列的改进算法。Yang[5]首次提出子空间跟踪算法，通过自适应迭代策略来逼近相关矩阵的主特征向量，解决了特征分解算法复杂度较高的问题。张红波等[6]进一步研究这种算法思想，并通过滑动窗技术估计直扩信号同步位置，降低了计算量。沈斌等[7]对特征分解算法和最大范数法进行结合，改进了估计效果。

分析传统扩频序列估计算法可以看出，常规算法需要借助其他算法对直扩信号的延时进行估计，避免非同步模式下扩频序列需要拼接而产生相位模糊的问题。本文总结传统算法的思路，并在此基础上提出了倍窗口相参子空间投影扩频序列估计算法，解决了非同步模式下扩频序列估计算法的相位模糊问题，并通过相参合并的方法综合利用多次投影追踪得到的扩频序列片段，进一步提高了算法性能，最后通过仿真试验验证了算法的有效性。

1 常规扩频信号扩频序列估计算法

1.1 扩频信号模型

考虑到传输延时，接收到的直扩基带信号可以表示为

x(t)=Ad(t-T0)c(t-T0)+n(t)。

(1)

式中：A是信号的幅值；d(t)为脉冲宽度为Tb的调制序列，其信息速率为Rs=1/Tb；c(t)为脉冲宽度为Tc扩频序列，扩频码码片速率为Rc=1/Tc，扩频码周期为PTc，P为扩频序列码长；T0为[0,PTc]上均匀分布的随机延迟值；n(t)为高斯白噪声。当T0=PTc时采样信号的起始点恰好为扩频序列的起始位置，此时称为同步模式[2-3]。

1.2 特征分解算法

特征分解法是一种经典的扩频序列估计算法[3]，在接收直扩信号没有进行同步处理时，只需己知码周期先验条件，对直扩信号数据建模为数据矩阵，进行特征分解，由两个主特征值对应特征向量实现扩频序列的恢复。算法流程如下：

Step1 假设已经获取了直扩信号码周期长度Tb，接收端将采集的直扩信号分割成长度为Tb的不重叠数据段，每个数据段构成一个观测向量。将所有的观测向量依次排列并用矩阵形式表示为

X=[x1,x2,…,xN]。

(2)

式中：矩阵X的每一列xi表示一段长度为Tb的直扩信号，其表达式为

xi=[x(1+iTb),x(2+iTb)…x(j+iTb)],j=1,2,…,Tb。

(3)

采样信号构建观测矩阵X的过程如图1所示。

图1 扩频信号观测模型

(4)

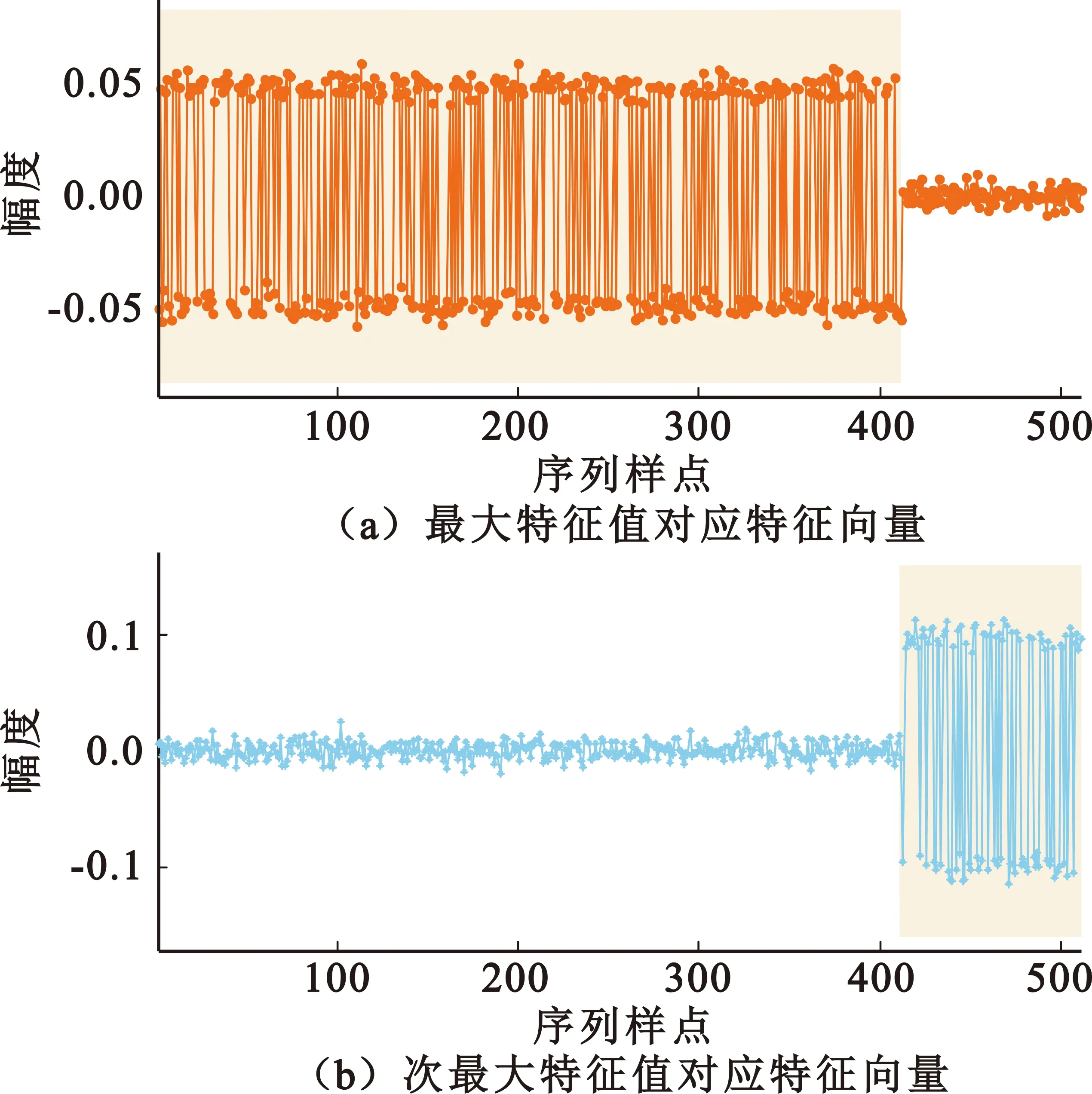
图2 非同步模式矩阵分解扩频序列估计结果

矩阵特征分解法可以实现扩频码序列估计，但该算法需要等待所有测试数据全部接收后才能进行一次估计，算法实时性较差。

1.3 投影逼近子空间跟踪算法

投影逼近子空间跟踪(Project Approximation Subspace Trace，PAST)算法将特征向量的估计转化为求解代价函数最小值的最优化问题，通过梯度下降法对信号进行自适应跟踪，最终提取出扩频序列[5-6，8]。PAST算法与特征分解算法相比较减少了矩阵特征分解过程，提高了算法的自适应性。

算法需要获取直扩信号的扩频周期Tb，将直扩信号按照长度Tb分段，得到矩阵X=[x1,x2,…,xn]，每一列表示一个完整扩频码周期信号数据。初始化特征值参数w1=rand(Tc),w2=rand(Tc)，跟踪参数μ,N。步长μ的参数设置为10-5，小的值可以适应信噪比较低的扩频信号。

按照以下步骤进行迭代运算：

Step1 取出一段长度为Tc的信号xi。

Step2 使用特征向量w1对采样信号xi进行投影运算：

y1(k)=w1T(k-1)xi(k)。

(5)

Step3 计算误差：

Δw1=[(xi(k)-w1(k-1)yj(k)]y1H(k)。

(6)

Step4 利用误差更新特征向量：

w1(k+1)=w1(k)+μΔwj。

(7)

Step5 从信号中减去估计出的特征向量：

xi′(k)=xi(k)-Δw1y1。

(8)

Step6 使用特征向量w2对剩余信号xi′进行跟踪，重复Step 2～5。

投影逼近子空间跟踪算法用y(i)=wT(i-1)x(i)近似表示向量x(i)到向量w(t)上的投影，同时算法使用了串行干扰消除的策略，首先估计出最大的特征分量w1，然后将该分量从总信号中减去，最后从剩余信号中估计次最大特征分量w2，当算法收敛时使用两个特征分量w1、w2组合成完整的扩频序列。投影逼近子空间跟踪算法是特征值分解算法的迭代运算，可以通过贯序处理的方式估计扩频序列。

矩阵特征值分解算法与投影逼近子空间跟踪算法存在以下缺点：

(1)两种算法在非同步模式下存在相位模糊的问题，得到的两段扩频序列片段幅度可能是相反的，不能直接拼接组成一个完整的扩频序列；

(2)空间投影算法需要进行两次迭代跟踪，存在误差累积的现象，第二次跟踪收敛速度较慢；

(3)矩阵分解算法在较低信噪比条件下需要较大的信号样本数量，计算延时较大。

针对以上存在的问题，本文提出一种倍窗口相参空间追踪算法。

2 倍窗口相参子空间投影算法

PAST算法的本质是提取信号自相关矩阵的特征值，第一次跟踪的结果为最大特征值对应的特征向量[3]，特征向量的本质是数据的高维正交分解坐标轴，主特征向量表示数据的主要维度。直扩信号为调制比特与扩频序列相乘结果，扩频序列表示了直扩信号的主要维度。在非同步模式下，第一次和第二次收敛的结果w1、w2分别包含扩频序列的两个片段，因此当使用两倍扩频周期长度为窗口截取信号，得到矩阵X=[x1,x2,…,xn]，并对协方差矩阵进行特征分解后，其主要特征向量包含完整扩频。利用这一思想，提出了倍窗口相参子空间投影跟踪算法。

假设已经获取了扩频周期长度Tb[10]，算法步骤如下：

输入：信号S，扩频码长Tc，迭代次数iter_N，初始化特征向量w1、w2、w3。

Step1 将直扩信号按照扩频序列两倍长度2Tb分段，每段信号表达式为

xi=s((i-1)×2Tb+1:i×2Tb)。

(9)

Step3 估计同步位置T0：

(10)

(11)

Step5 判断w2′、w3′与w1′的极性关系：

(12)

(13)

Step5 将w1′、w2′、w3′相参合并：

w=w1′+ω2w2′+ω3w3′。

(14)

Step6 对w进行判决，得到扩频序列。

由于在进行串行干扰消除运算时存在误差累积的现象，因此等待Step 2完成iter_N次迭代后启动Step 3～6完成相参合并运算。也可在Step 1中只对特征向量w1进行迭代处理，通过Step 1～3直接获取扩频序列。

3 算法仿真

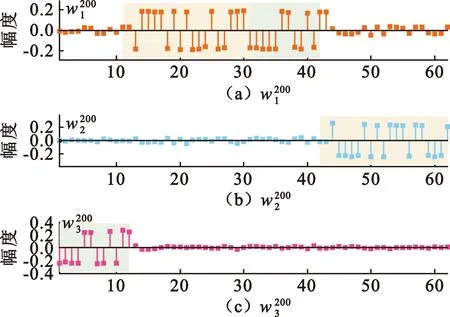
图3 算法特征向量迭代结果

为了比较扩频序列的误码率性能，生成一段BPSK直扩信号，设置码长为512，码速率1 Msample/s，采样率4 Msample/s，信噪比-16 dB，统计不同迭代次数下w1、w2、w3对应扩频序列误码率性能以及与扩频序列之间的相关值，并与相参合并后的结果及传统PAST算法进行比较，统计结果如图4所示。

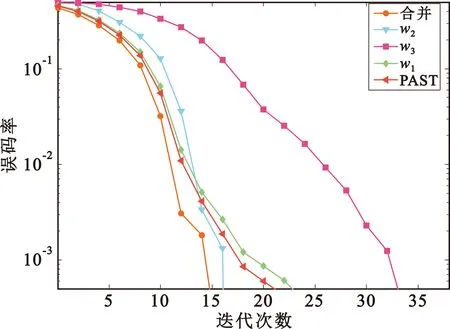
(a)不同迭代次数下误码率性能

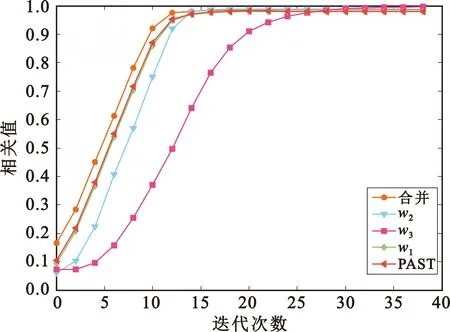
(b)不同迭代次数下与阔怕序列相关性能图4 算法误码率与相关性能

对比图4中w1、w2、w3与相参合并结果的性能可以看出，相参合并运算进一步提高了扩频序列估计结果的误码率性能以及相关度性能，同时还可以看出经过相参合并后的误码率性能优于传统PAST算法。

为了验证不同迭代阶段相参合并结果w的幅度分布情况，生成一段BPSK直扩信号，设置码长为512，码速率1 Msample/s，采样率4 MHz，信噪比-10 dB，分别统计1～100、100～200、200～300次迭代时w的幅度分布，结果如图5所示。

图5 倍窗口相参子空间投影算法迭代结果热力图

从图5中可以看出，算法迭代1～100次时幅度分布较为散乱，结果可信度较差；在进行100～300迭代后时结果可信度较高，但受到噪声的影响，幅度仍旧在一定幅度内小范围抖动。

4 结 论

本文提出了一倍窗口相参子空间投影扩频序列估计算法，利用提取扩频序列两倍扩频周期长度数据进行迭代的思路，解决了常规算法工作在非同步模式下存在相位模糊的难题，同时通过相参合并三个扩频信号片段进一步提高了估计结果的准确性。仿真结果证明了算法的有效性，算法具有一定的工程应用价值。