面向数据采集的多无人机协同节能部署方法*
袁 进,王 海,秦 蓁,李艾静
(中国人民解放军陆军工程大学 通信工程学院,南京 210007)
0 引 言
随着无线网络技术的发展,无人机以其机动性高、部署灵活和成本低等优点,被广泛应用于军事和民用领域,如实时监视、侦察行动、搜索和救援行动和农业灌溉等[1]。同时,无人机通信技术被认为是5G中解决偏远地区信号覆盖、应急通信和动态数据采集的关键技术,其可以动态和选择性地增加网络容量[2]。在物联网(Internet of Things,IoT)中,无人机作为数据汇集节点,可以实现数据的高效采集:一方面与地面基站相比,无人机可以根据数据采集的需求动态调整位置,从而减少设备与无人机之间的传输距离;另一方面,调整无人机的高度可以增加视距链路的概率,从而减少设备数据传输的能量损耗。因此,为了充分利用无人机的优势,需要精心设计无人机的三维部署以及物联网设备的功率控制和关联情况。
现有文献对无人机辅助通信进行了大量的研究。文献[3-6]虽然考虑了地面设备的通信需求不同,但是只考虑如何实现覆盖的用户数量最大化,而没有考虑无人机系统的节能部署问题。文献[7-10]考虑了无人机的能量限制,以最小化系统的总传输功率实现无人机网络的节能部署,但是文中只考虑无人机的资源限制,而没有考虑地面设备的通信需求的差异化。与此同时,对无人机的三维部署优化时,大多数文献都是采用降低维度的处理方式[3-8],将三维位置分解为水平位置和高度位置进行优化,两者间通过公式近似求解,而且地面设备无法始终与无人机保持最佳仰角,直接通过公式计算将导致误差。因此优化无人机的三维部署时,应避免采用降低维度的处理方法。
本文研究如何部署多架旋翼无人机对具有差异性服务质量(Quality of Service,QoS)需求的物联网设备执行数据采集任务,通过联合优化无人机的三维部署和设备关联,以节约物联网设备的功率资源。
1 系统模型
1.1 网络模型
考虑IoT中一个区域突发自然灾害,附近的地面基站均被破坏,由于单架无人机的能量有限且效率低下,因此本文考虑使用K架无人机协同完成数据采集任务,系统模型如图1所示。地面有M个物联网设备需要在规定时间T0内将采集的数据信息上传,然而每个物联网设备的数据采集量不同,为了尽快完成数据上传任务,每个设备应采用不同的数据传输速率,即QoS需求不同。虽然多无人机网络中存在干扰问题,但是实际中存在多种干扰消除技术可减少干扰,如频率划分、非正交多址技术、合作非正交多址技术等[5],因此本文不考虑干扰的影响。
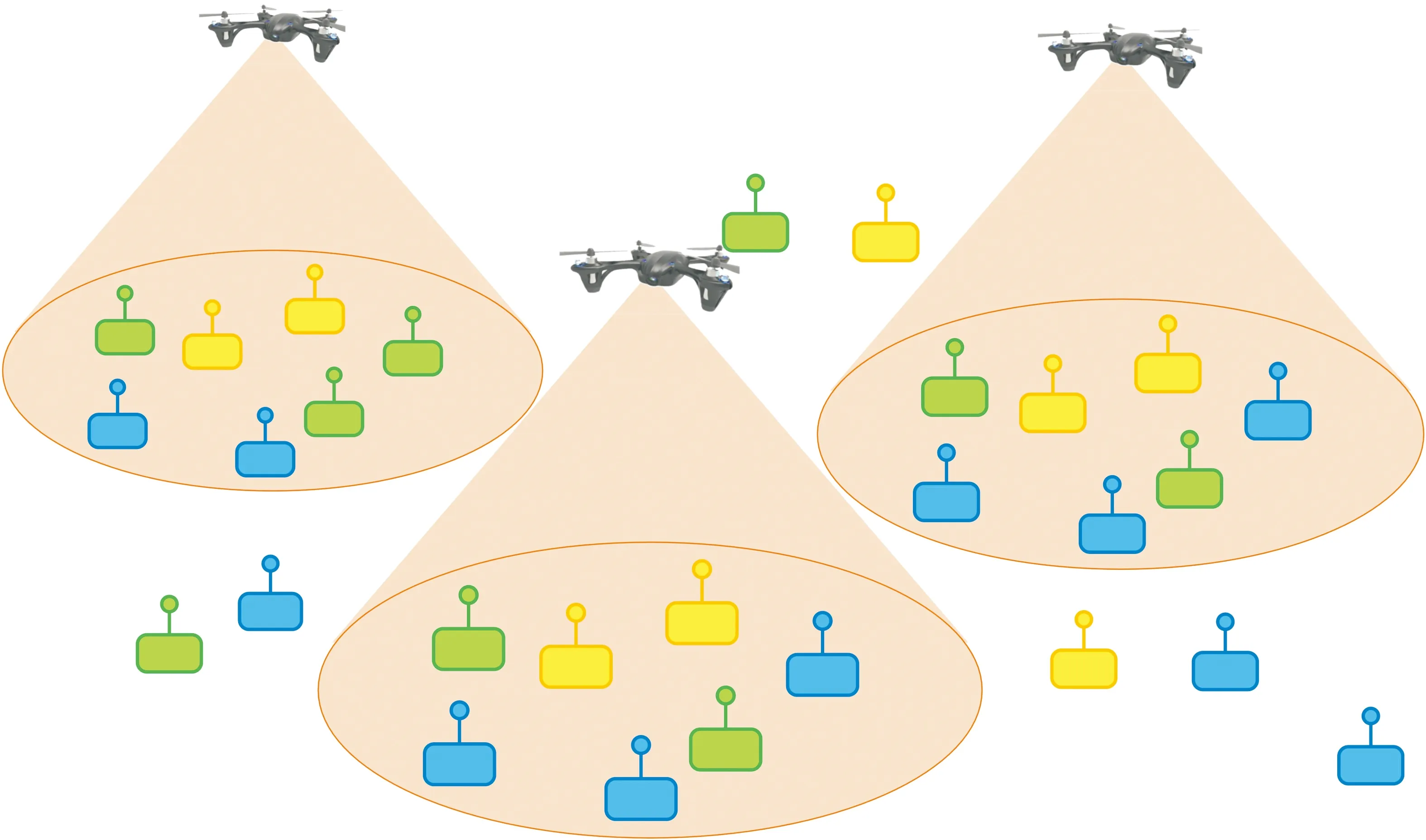
图1 系统模型图
假设设备的地理位置是已知的,无人机k和设备m的集合分别为K={1,2,…,K}和M={1,2,…,M},地面设备的三维坐标为gm=(gm1,gm2,0),无人机的三维位置为uk=(xk,yk,hk)。本文考虑上行物联网场景,其中每个物联网设备采用正交信道传输数据,最多只能被一架无人机服务。同一架无人机服务的设备在正交时隙中传输数据,而不同无人机服务的设备采用不同的频带传输数据,从而避免干扰。对于任意的m∈M和k∈K,二进制变量am,k表示设备与无人机之间的关联关系。如果am,k=1,则表示设备m与无人机k关联;如果am,k=0,则表示不关联;与此同时,∑am,k≤1表示每个设备最多只能被一架无人机服务。λm表示设备m需要上传的比特数,λk表示无人机k可接收的最大比特数(即无人机k的容量限制)。
1.2 空地信道模型
假设设备m的传输功率为pm∈[0,pmax],其中pmax为设备的最大传输功率。此时设备m和UAVk之间的信噪比为
(1)
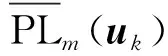
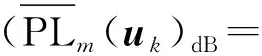
(2)
(3)
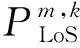
(4)
(5)
(6)
式中:ψ和β是取决于载波频率和环境类型的参数,θm(uk)是设备m与无人机k之间的仰角。由(6)可知,随着无人机k的飞行高度(即hk)的增加,设备与无人机k的仰角增加,从而LoS的概率也会增加。但是随着飞行高度的增加,无人机与设备的距离也会增加,从而导致路径损耗增加。因此,无人机的飞行高度要谨慎选择,以权衡LoS的概率和路径损耗。
根据公式(2)~(6),设备m与无人机k之间的路径损耗为
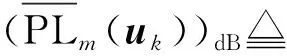
(7)
1.3 问题公式化
本文的主要目标是确定无人机的三维部署uk以及设备关联{am,k,∀m,k},以最大程度地节约物联网设备的功率资源。因此,联合优化无人机的三维部署和设备关联问题(P1)可以表述为
该优化目标表示的是物联网设备相对于以最大传输功率传输数据时,节约的功率资源的总和。C1确保每个物联网设备最多只与一架无人机相关联;C2确保每架无人机关联的物联网设备所上传的比特数之和不能超过该无人机的缓存容量限制;C3为了确保数据成功传输,因此与无人机关联的设备的信噪比应大于阈值;C4和C5分别提供了无人机的飞行高度和设备传输功率的上下界。
经分析可知,问题P1是一个混合整数非线性规划问题,它由整数和实数变量组成,而且无人机的三维部署和设备关联问题之间存在耦合,无人机的部署位置会影响设备的关联情况,同时设备的关联也会影响无人机的最佳部署位置,因此该联合优化问题无法直接求解。
2 联合三维部署和设备关联算法
2.1 节能关联算法优化设备关联
固定无人机的三维部署uk=(xk,yk,hk),研究设备关联问题,即{am,k,∀m,k}。该问题可以被建模为一个0-1多背包问题,于是提出一种基于动态规划的节能关联算法(Energy-saving Association,ESA)求解。
当固定无人机的三维部署即uk=(xk,yk,hk)时,问题P1可以简化为问题P2:
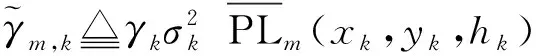
为了解决多背包问题,本文提出了一种两阶段的节能关联算法。首先并行求解多个基本0-1单背包问题,然后根据节约功率最大化的原则对重叠设备关联的无人机进行重新分配。
2.1.1 阶段1:0-1单背包问题[14]
在阶段1中,根据无人机的数量,将问题分解为K个背包问题。每架无人机不考虑其他无人机的关联情况,单独解决基本的0-1单背包问题,找出每架无人机的关联设备集合:
(8)
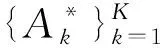
2.1.2 阶段2:节约功率最大化分配
在阶段2中,主要解决多架无人机之间存在重叠关联设备的问题。无人机之间相互交换信息,确定存在重叠设备的无人机k′,然后根据公式(9)将重叠设备分配给节约功率资源最大的无人机。
(9)
第二阶段结束后,部分无人机将释放容量。为了充分利用无人机的剩余容量,每次循环都将更新无人机的容量和备用的关联设备集合,然后反复执行上述两个阶段,直到无人机的关联设备不再改变。该两阶段的节能关联算法(算法1)总结如下:
输入:物联网设备分布的地理位置gm=(gm1,gm2,0),无人机的三维部署位置uk=(xk,yk,hk)以及无人机k和设备m的数量。
1 初始化:对于所有的无人机k和设备m,令am,k=0,寻找每架无人机k可连接的设备集合Mk。
3 fork=1:Kdo
5 end
6 fork=1:Kdo
7 对于所有的元素m∈Mk,根据公式(9),确定设备和无人机之间的关联关系,更新am,k。
8 end
9 更新所有无人机k的剩余容量和对应的备用关联集合。
10 end while
11 返回{am,k,∀m,k}
2.2 粒子群算法优化三维部署
本节研究在已知设备关联集合的情况下,无人机如何根据设备的需求获得最佳的三维部署。因此,将问题P1中的最大化问题分解为K个最小化子问题P3,由无人机k并行解决最小化子问题。
式中:C1是限定无人机的部署的高度,保证无人机可获得较高的视距传输概率,同时确保无人机与设备始终处于连接状态;C2是保证物联网设备在无人机的最大覆盖范围内。针对问题P3,本节采用基于设备通信需求的粒子群(Particle Swarm Optimization,PSO)算法优化无人机的最佳三维部署。
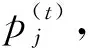
(10)
(11)
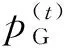
(12)
(13)
更新所有虚拟粒子j下一次迭代中的速度和探测位置,具体公式如下[16]:
(14)
(15)
式中:ω为惯性权重,其取值范围0<ω<1;κ1和κ2为非负实数,本文令κ1=κ2=1;r1和r2为0~1之间的随机数。
粒子群算法优化三维部署(算法2)具体如下:
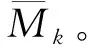
输出:无人机的部署位置uk,best。
1 初始化:将无人机k随机部署在对应的设备关联集合内,初始化相关参数,随机产生一组虚拟粒子,设t=1。
2 循环开始:
3 每个虚拟粒子根据其所在位置计算适应度值,即设备的传输功率总和:
4 根据公式(11),更新每个虚拟粒子当前的最佳部署位置XL,j。
5 各粒子间交互信息并根据公式(13),更新当前探测到的全局最佳部署位置XG。
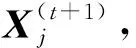
7 若t=T或所有虚拟粒子已收敛至同一位置,循环结束;否则,返回循环。
8 返回uk,best=(xk,best,yk,best,hk,best)。
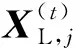
证明:探测粒子速度和位置的更新公式(14)和(15)闭合形式可以表示为[15,17]
(16)
式中:
(17)
(18)
(19)
(20)
(21)
显然,若max(‖φ1‖,‖φ2‖)<1,则
(22)
那么
(23)
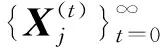
(24)
解不等式(24),可得
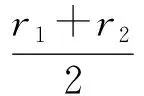
(25)
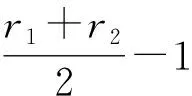
证毕。
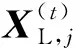
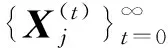
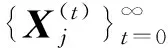
(26)
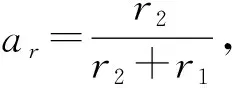
证毕。
根据引理1可知,所有探测粒子将收敛至当前全局最优位置。但是需要说明的是,探测到的当前全局最优位置并不一定就是全局最优部署位置。粒子群算法收敛于全局最优部署位置的概率与探测粒子的数量密切相关。由图2可知,当探测粒子的数量增加,PSO算法的探索能力会提升,则最终收敛于全局最优部署位置的概率就越大;反之,当探测粒子数量较少时,易陷入局部最优的概率就会增加,且收敛速度会减慢。
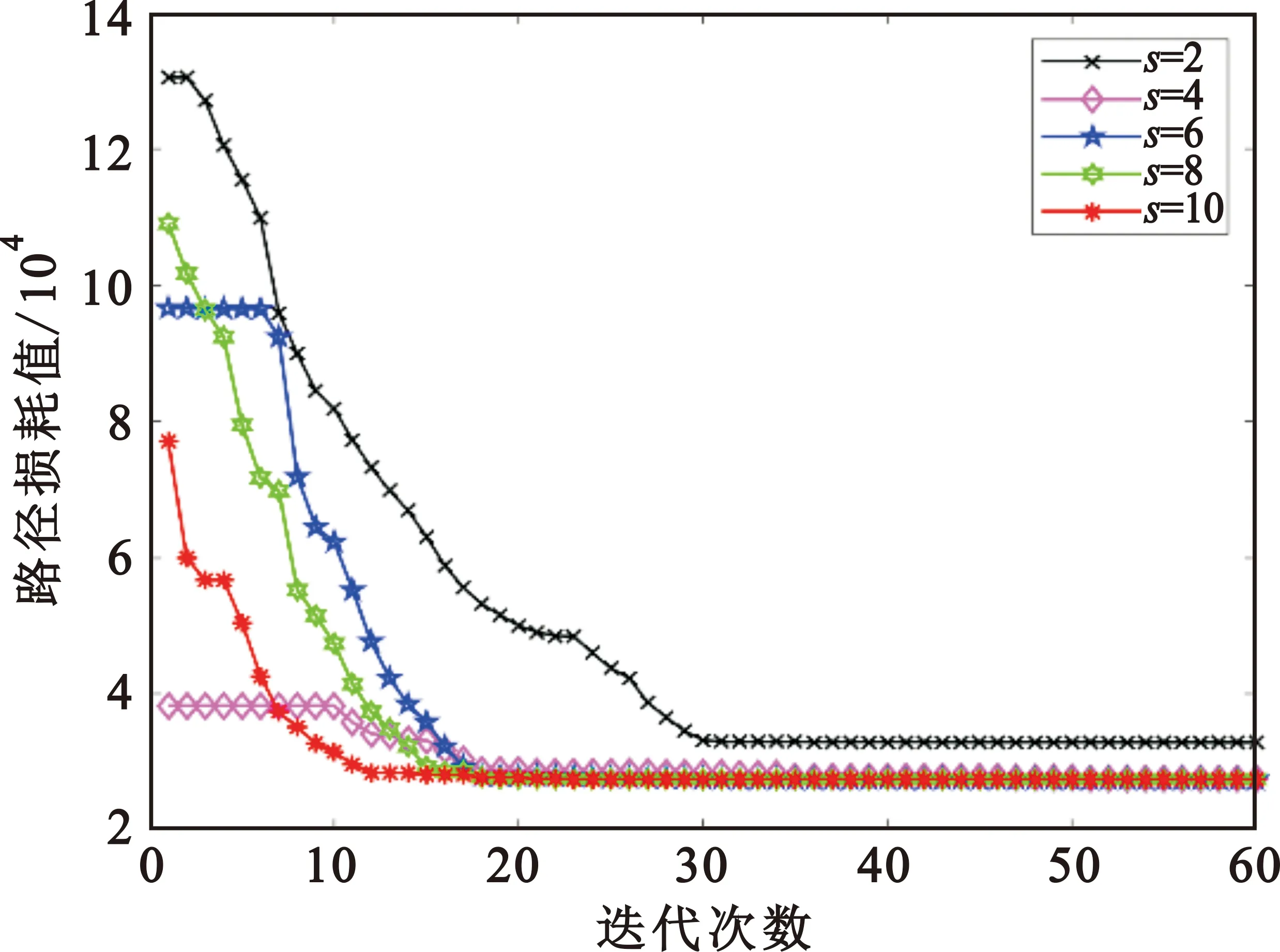
图2 粒子数量对PSO算法收敛性的影响
2.3 交替迭代优化方法
在2.1和2.2中,分别提出了算法1和算法2解决问题P2和问题P3,本节基于前面两节所提出的方法,提出一种交替迭代的优化方法(算法3)解决问题P1,即联合优化无人机的设备关联和三维部署。交替迭代的优化方法的实现过程如下:
初始化:初始化相关参数,将无人机k随机部署在目标区域内,设置t=1。
循环开始:
1 固定无人机的部署位置,用算法1优化无人机的关联设备集合。
2 固定无人机的关联设备集合,用算法2优化无人机的三维部署位置,设置t=t+1。
3 若t=T,循环结束;否则,返回循环。
2.4 复杂度分析
本文提出的交替迭代算法由两个子算法构成:节能关联算法(算法1)和粒子群算法(算法2)。算法1将问题P2分解为K个单背包问题,因此其计算复杂度为O(K2T1),K为无人机的数量,T1为算法1的迭代次数。算法2的计算复杂度为O(sT2),s为粒子群算法中虚拟粒子的数量,T2为算法2的迭代次数。本文将问题P1分解为K个P3子问题,因此粒子群的计算复杂度为O(sKT2)。综上所述,本文提出的交替迭代算法(算法3)的计算复杂度为O((K2T1+sKT2)×T3),其中T3为算法3的迭代次数。
3 算法仿真与分析
3.1 仿真设置
本节对提出的交替迭代部署算法进行仿真分析,仿真平台为Matlab 2019a。考虑一个大小为600 m×600 m的区域,其中部署了M个物联网设备,其分布遵循齐次泊松点过程。物联网设备的通信需求在[1,10]个单位中任意选择,无人机的容量限制为500个单位,其他的仿真参数如表1所示[14]。
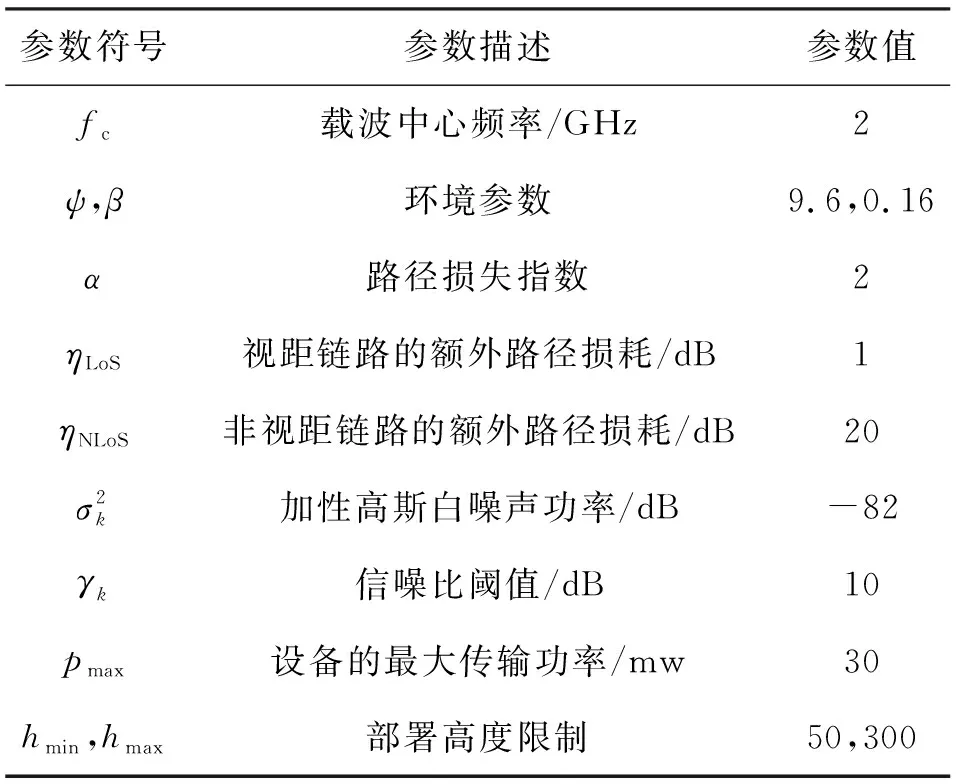
表1 部分仿真参数的设置
为了验证所提出算法(ESA+PSO,简称为EP算法)的性能,本文实现并比较了以下算法:
(1)聚类算法——使用K-means算法将物联网设备分成K个簇,即每架无人机的关联设备。将无人机的水平位置设置在每个簇的簇心,然后根据传输功率最小化的原则优化无人机的部署高度。
(2)GP算法(Greedy+PSO)——首先根据设备的潜在节约功率进行选择性服务,然后根据设备的通信需求结合粒子群算法优化无人机的三维部署。
图3展示了当无人机数量为3、设备数量为400时,设备与无人机的关联情况以及无人机的三维部署。图中三种颜色的五角星代表三架无人机,其中小五角星表示无人机在迭代过程中的位置变化,而最后的大五角星表示无人机的收敛位置。与每架无人机颜色对应的实心圆表示无人机对应的关联设备,其中的黑色空心圆圈表示未被无人机关联的设备。由图可知,随着迭代次数的增加,无人机的三维部署位置也随之改变,最终收敛至同一位置,说明该算法具有收敛性。
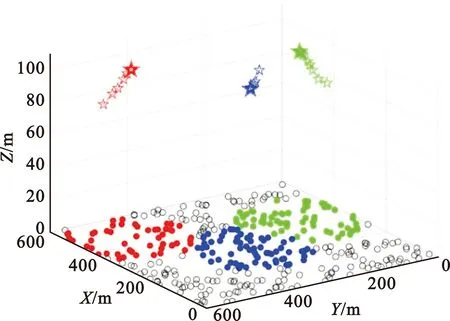
图3 多无人机协同的三维部署图
3.2 性能分析
本节主要分析多种通信环境和设备的总节约功率的影响。根据文献[11-12]所提的信道模型,信道参数在不同的通信环境下的取值是不同的,表2给出了“Suburban”“Urban”“Dense urban”三种通信环境下的信道参数[15]。所提算法在不同通信环境下的收敛情况如图4所示,其中无人机的数量为4,地面的物联网设备数量为300。由图可知,随着迭代次数的增加,网络的总节约功率也随之增加,最终收敛至网络的总节约功率的最大值。在不同的通信环境下,网络的总节约功率是不同的。在“Suburban”环境下的网络总节约功率最大,原因在于无人机网络在“Suburban”环境下获得的LoS传输概率要比“Urban”和“Dense urban”环境中获得的LoS传输概率要大。
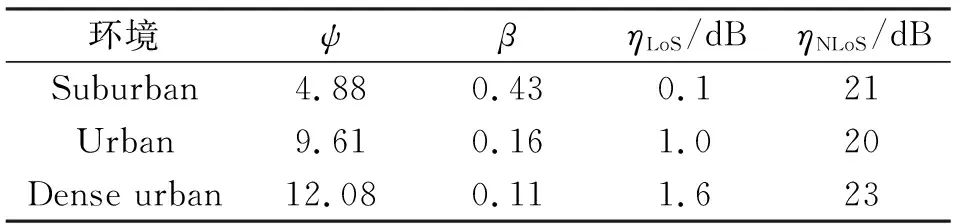
表2 不同通信环境下的信道模型参数
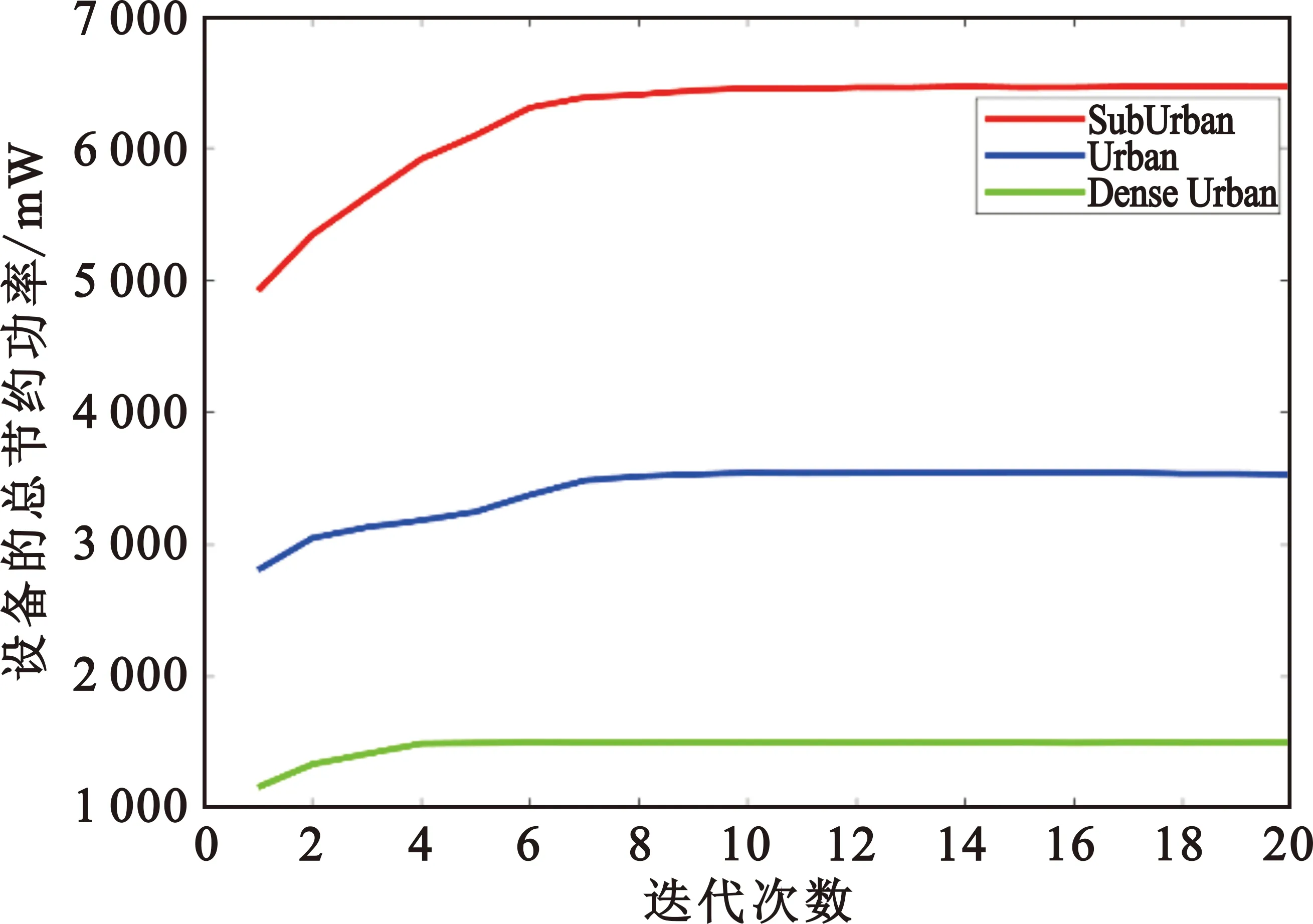
图4 通信环境对算法收敛性的影响
图5展示了当无人机数量为3时,随着设备数量的变化,各算法的总节约功率的变化情况。由图可知,随着设备数量的增加,EP算法和GP算法的总节约功率也随之增加,而聚类算法的总节约功率保持相对静态。因为聚类算法关联设备时没有考虑设备的传输功率和通信需求,只是单纯地根据用户之间的距离进行聚类关联。当设备数量越多时,本文提出的EP算法性能优势越明显。因为当无人机的服务容量有限时,设备之间的竞争会更加激烈,此时合理的设备关联方法将变得十分重要。相比之下,GP算法的性能始终低于EP算法,因为GP算法的只是单纯的“利己主义”,而没有考虑其他无人机的设备关联情况。
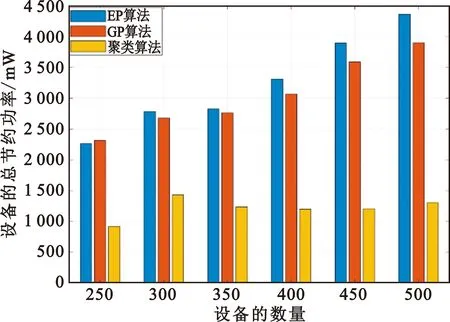
图5 总节约功率与设备数量的关系
图6展示了当设备数量为500时,随着无人机数量的增加,各算法的总节约功率的变化情况。由图可知,随着无人机数量的增加,三种算法对应的总节约功率也随之增加。因为随着无人机数量的增加,无人机可服务的设备数量增加以及设备与无人机之间的距离减小,减少了设备的传输功率损耗。但是当无人机数量为6和7时,聚类算法的性能提升明显,甚至超过了GP算法,因为当无人机数量较多时,设备与无人机之间的距离较短。在迭代的过程中,GP算法的部分无人机会争夺其他无人机关联的设备,以寻求自身关联设备的最大化。相比之下,聚类算法将设备分簇,减少无人机之间的竞争。同时,无论无人机数量如何变化,本文提出的EP算法的性能依然是三者中最好的。
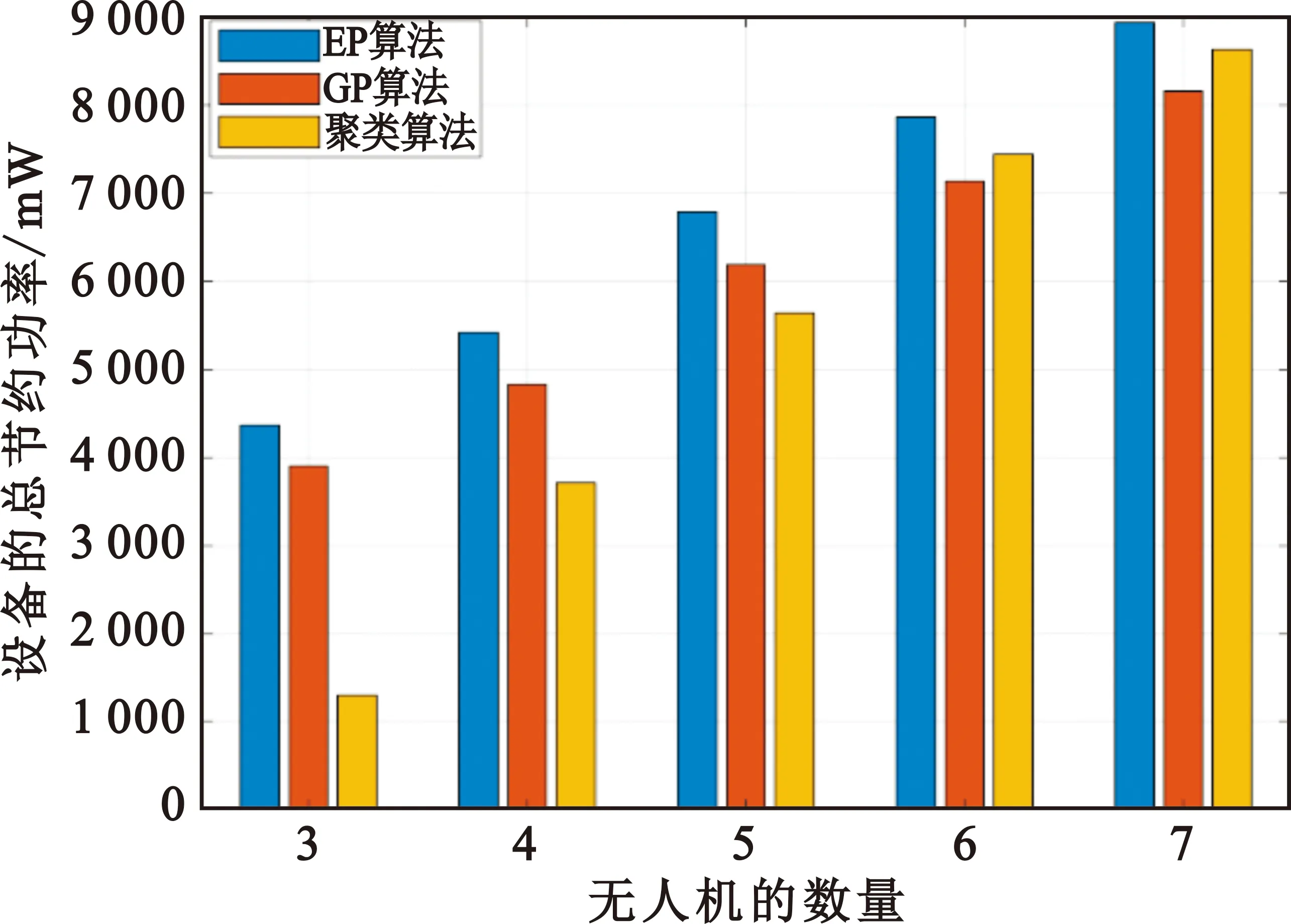
图6 总节约功率与无人机数量的关系
4 结束语
本文针对具有差异化服务质量需求的数据采集任务,提出了一种多无人机协同部署策略。该策略将初始问题转化为设备关联子问题和无人机三维部署子问题,进行交替迭代求解。在不同的网络设置下进行了大量的仿真,以评估所提出算法的性能。仿真结果表明,与其他对比算法相比,本文所提出的策略获得了明显的性能提升。在后续的工作中,我们将考虑多无人机之间的干扰问题和异构无人机的协同覆盖问题。

