一种基于车边云协同的车联网计算卸载策略*

罗 优,李 晖,2,周又玲,王 萍,林志阳

(1.海南大学 信息与通信工程学院，海口 570228；2.南京信息工程大学滨江学院，江苏 无锡 214105)

0 引 言

随着城市化进程的快速推进以及汽车数量的飞速增长，道路安全、交通效率和环境污染等一系列交通问题日益突出。为了建立更加安全、绿色、高效的交通管理系统，实现人、车、环境的协调发展，车联网技术应运而生。车联网(Internet of Vehicles，IoV)通过车内、车与车、车与路、车与人、车与服务平台的全方位万物互联，可实现智能交通管理控制、车辆智能化控制和智能动态信息服务的一体化。随着车联网的迅速发展，一系列涵盖行驶安全、交通效率和车辆通信服务的车载应用也随之迅速发展，如自动驾驶技术、增强现实技术等。

当前车载技术无法满足日益增长的车载应用对时延的需求[1]，将移动边缘计算(Mobile Edge Computing，MEC)集成到通信网络架构中，可以有效解决车联网中计算密集型任务和延迟敏感型任务所导致的指数级增长的移动流量，因为在物联网业务场景中，边缘模块[2-3]可以提供低业务延迟、低能耗、适当的缓存、快速的通信和灵活的计算。Cui等人[4]提出了一种联合云计算、移动边缘计算及本地计算的多平台智能卸载方案，根据任务属性利用强化学习算法选择卸载平台，旨在最小化时延并节省系统总成本，但所提网络模型中的控制面和数据面是深度耦合，使得任务处理缺乏灵活性。Zhang等人[5]提出了一种基于分层云的车载边缘计算卸载框架，通过引入邻域中的备份服务器来解决MEC服务器计算资源有限问题。Li等人[6]提出了一种新的架构，它结合了远程中央云、附近的边缘计算服务器和车载云，以扩展车辆移动应用的可用云服务。基于云的MEC卸载框架的提出能够进一步降低任务持续时间，包括移动设备将任务卸载到云端的传输时间、云中的执行时间以及云发送的传输任务结果到移动设备的时间，同时减少移动设备的能耗和传输成本。左超等人[7]提出了一种面向设备优先级的贪心算法，通过对每个设备能耗和 CPU 占用率设定优先级，获得当前最优的任务分配方案，同时采用结合面向设备优先级的贪心策略的粒子群算法优化提出的贪心算法。

朱新峰等人[8]基于“分治”的思想，提出了一种考虑用户综合需求的动态资源分配策略，进行计算资源和频谱资源的分配以寻求吞吐量和时延性能方面的提升。Ning等人[9]在智能车联网中构建了一个三层卸载框架，以在满足用户延迟约束的同时最大程度地降低总体能耗，提出了一种基于深度强化学习的方案来解决优化问题。刘斐等人[10]分析了边缘计算服务器容限阈值和车辆密度对平均等待时延和卸载成功率的影响。

上述文献大多考虑计算卸载过程中资源分配、设备能耗及传输成本问题，但对于任务具体卸载策略研究较少。本文通过采用“车-边-云”协同卸载网络架构，并采用粒子群优化(Particle Swarm Optimization,PSO)算法对卸载系数和任务分配系数求解，得到最佳卸载方案，实现车辆卸载时延最小化。

1 系统模型

1.1 网络模型

在车联网中，本文选取一个由车辆、移动边缘设备、云组成的三层网络架构，其架构如图1所示。该车联网架构由终端车辆端、MEC边缘计算服务器以及云服务器组成。终端车辆可以与其他设备进行无线通信。MEC边缘计算服务器由固定边缘节点和移动边缘节点组成，移动边缘节点由用户终端附近的带有可用计算资源的移动车辆以及专门部署的移动服务器车辆组成，固定边缘节点由用户附近的带有MEC功能的路侧单元(Road Site Unit，RSU)以及部署了MEC设备的基站组成，其中边缘节点的计算能力各不相同，且固定边缘节点的计算能力强于移动边缘节点。中心云服务器有强大的计算、存储和网络资源，可进行快速的任务处理。

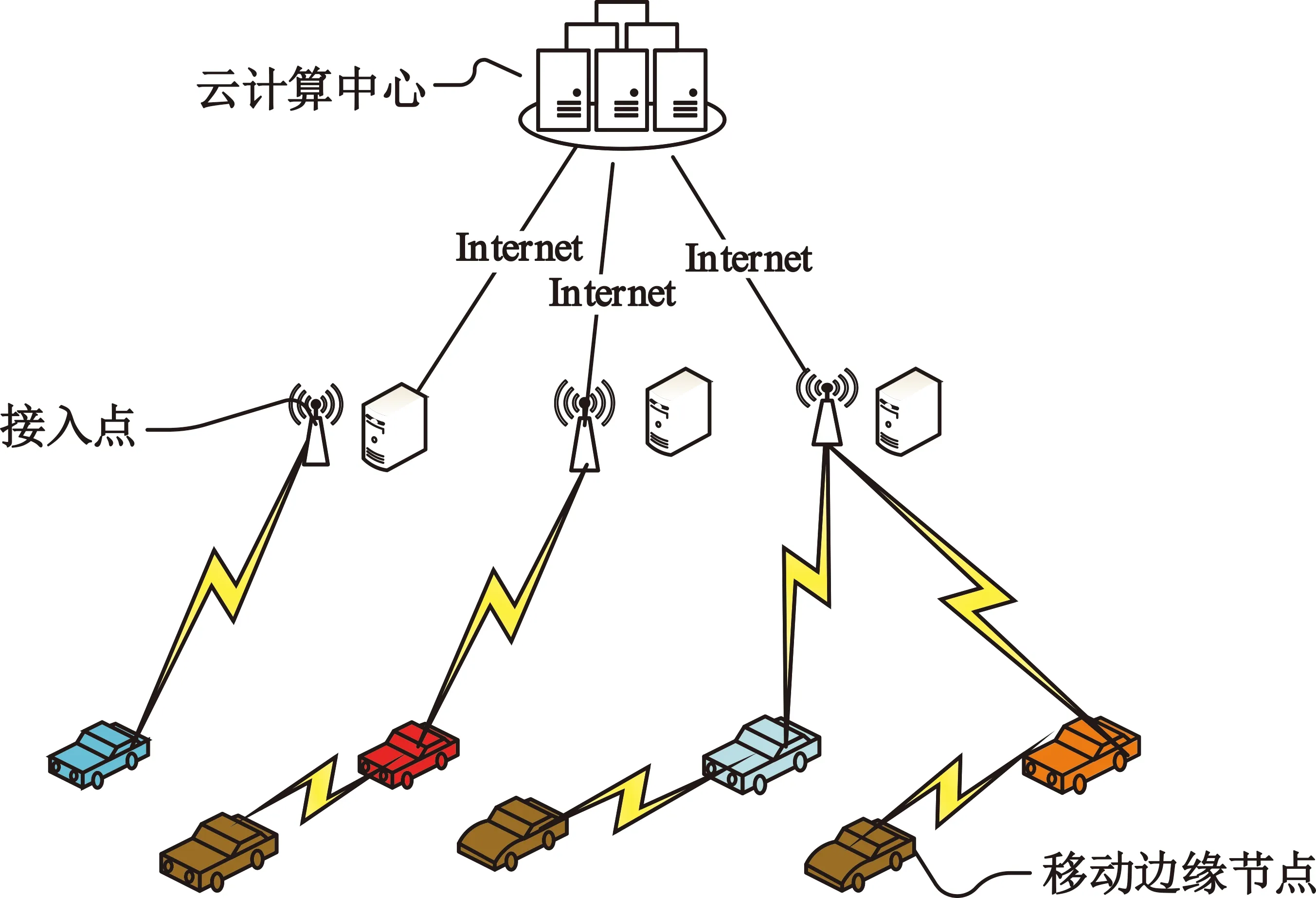
图1 车联网网络架构图

考虑将传统的RSU或基站作为一个接入点为车辆提供网络接入，但不进行计算卸载。假设在单向行驶的道路上有一终端车辆需要将一个计算密集型任务S进行卸载，该任务由云服务器、边缘节点、车辆本地CPU三者联合共同卸载。假设该任务可以按任意比例划分成多个子任务，子任务之间不存在重叠。假设卸载θS至MEC边缘节点，那么剩余任务总量为(1-θ)S,u(1-θ)S表示卸载至云服务器的任务大小，那么剩余任务(1-θ)(1-u)S在车辆终端CPU进行计算。其中，θ表示卸载至边缘计算的卸载系数，u表示卸载至云计算的卸载系数。设完成计算任务下的CPU周期数为C=aD，其中，a表示计算任务的计算复杂度，任务不同，计算复杂度就不同(例如对同一个视频，可以有剪辑、去噪、去水印等不同复杂度的操作)；D表示任务的输入数据大小[11]。因此，计算任务的总时延包括本地计算时延、边缘计算时延、云计算时延。

1.2 计算模型

假设有g个移动边缘节点，r个固定边缘节点。移动边缘节点和终端车辆都在同一个接入点RSU的覆盖范围内，移动边缘节点的坐标随机分布在50 m×200 m的道路上。di,dot为终端车辆到边缘节点的距离，di,c为终端车辆与远端云的距离。假设移动边缘节点的坐标为{(m1,n1),(m2,n2),…,(mg,ng)}，接入点的坐标为(mdot,ndot)，则车辆i与接入点的距离公式可表示为

(1)

车辆与MEC服务器之间是通过LTE- Advanced无线直连的方式进行通信的，车辆上传链路的信道被认为是频率平坦型快衰落的瑞利信道。参考文献[12]，则车辆i至接入点传输速度为

(2)

接入点至车辆i传输速度为

(3)

终端车辆至远端云的传输速度为

(4)

式中：Bi,dot、Bdot,i为车辆i与接入点之间的带宽，Bv,c为车辆与云端的带宽，Pi和Pdot为车辆i和接入点的传输功率，N0表示高斯白噪声功率，h表示信道衰落因子，δ表示路径损耗常数。

1.2.1 MEC计算时延

假设总任务为S，卸载至MEC边缘节点的计算的任务为θS，任务θS先到达接入点，再由接入点将任务分配至各固定边缘节点和各移动边缘节点，可求得终端车辆至接入点的传输时延可表示为

(5)

接入点分配给移动边缘节点的任务为βiθS，βi表示卸载至边缘计算中单个固定边缘节点的任务分配系数，所以移动边缘边缘节点执行时延包括接入点将任务传输给移动边缘节点的传输时延和移动边缘节点自身处理时延，所以移动边缘计算节点的执行时延为

(6)

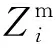
同理，固定边缘节点的执行时延为

(7)

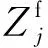
边缘节点执行时延为各边缘节点执行时延的最大值，因为分配给各边缘节点的任务不重叠，独立处理，因此边缘结点执行时延为

(8)

所以边缘计算总时延为终端车辆至接入点的传输时延和边缘结点执行时延之和为

(9)

运算结果的回传时延可忽略不计。

1.2.2 云计算时延

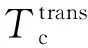
(10)

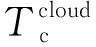
(11)

所以云计算的总时延为

(12)

运算结果的回传时延也可忽略不计。

1.2.3 本地终端处理时延

由上节可得，由终端车辆计算的计算任务为(1-θ)(1-u)S，可得车辆终端计算时延为

(13)

基于上述三部分的时延分析，总时延取各部分时延最大值，所以总时延可表示为Tt=max{TL,TC,TM}，即

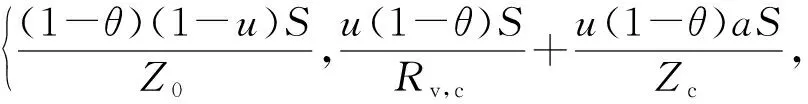
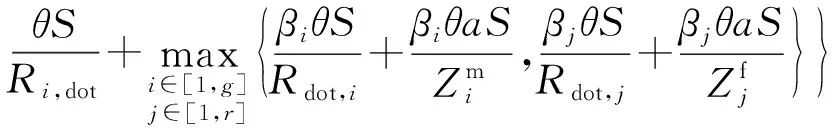
(14)

所以时延最优化模型为

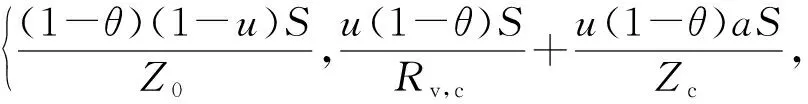
(15)

s.t. 0≤u≤1，

0≤θ≤1，

0≤βi≤1，

0≤βj≤1。

由于u、θ、βi、βj均为变量，为了求得时延最小，必须求出一组最优的u、θ、βi、βj。可将卸载系数和任务分配系数定义为一个(g+r+2)维的向量X=(x1,x2,…,xg,xg+1,…,xg+r,xg+r+1,xg+r+2)，其中，g为移动边缘节点个数，r为固定边缘节点个数，(x1,x2,…,xg)为各移动节点任务分配系数βi，(xg+1,…,xg+r)为固定边缘节点分配系数βi，xg+r+1表示卸载系数θ，xg+r+2表示卸载系数u，因此总时延公式的求解可以转化为对向量X的求解。于是总时延表达式可写为

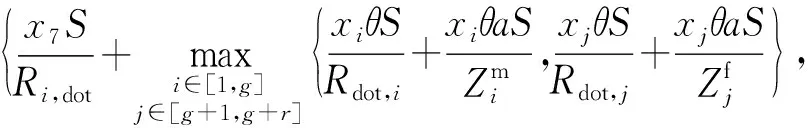
(16)

s.t. C1:0≤xi≤1,1≤i≤g+r+2，

式中：X∈J，J为可行解的搜索范围，C1表示不管是卸载系数还是边缘节点分配系数的范围在(0,1)之间，C2表示边缘节点中任务的分配系数之和为1。

2 基于粒子群算法的任务卸载策略

2.1 基本PSO算法

粒子群优化算法的基本概念源于对鸟群捕食的研究。PSO中，优化问题的潜在解都是搜索空间中的一只鸟，称为粒子。假定在D维搜索空间中，由M个粒子组成一个种群进行“飞行”(即搜索)，第i个粒子的位置表示为Xi=(xi1,xi2,…,xiD)，第i个粒子的速度表示为Vi=(vi1,vi2,vi3,…,vid)，每个粒子在飞行过程中搜索到的最好位置称为个体极值pbest=(pi1,pi2,…,piD)，整个种群搜索到的最好位置称为全局极值gbest=(gi1,gi2,…,giD)，粒子搜索过程中的速度和位置更新公式如下：

vid=wvid+τ1η1(pid-xid)+τ2η2(gid-xid) ，

(17)

xid=xid+vid。

(18)

式中：1≤i≤M,1≤d≤D;τ1、τ2为学习因子，通常设置为2；η1、η2是[0,1]之间均匀分布的随机数；w为惯性权重；vid∈[-vmax,vmax]，其中vmax是预先给定的最大速度。公式(17)中等号右边第一部分表示粒子当前状态;等号右边第二部分是粒子的自我学习部分，粒子对搜索历史过程的思考，引导个体最优位置方向运动;等号右边第三部分是社会认知部分，粒子群体通过相互交流向全局最优方向运动。

2.2 解决等式约束问题的PSO算法(FS-PSO)

基本的PSO算法中没有处理约束条件的机制。通常，粒子群算法求解有等式约束的优化问题的方法是将一个约束变为两个不等式约束，但很难随机产生可行解，导致收敛速度慢。为了解决本文时延公式中变量的约束条件，参考文献[13]和文献[14]的等式约束处理方法，可对本文的优化问题进行转化，从而求出最优解。因此，定义适应度函数为

(19)

式中：Ttmax为群体中最差可行个体的适应度值，

(20)

式中：δ是较小的整数。

FS-PSO粒子群算法的具体实现过程如下:

Step1 粒子群初始化：规定最大迭代数T；给定群体规模N，在可行域中随机产生每个粒子的位置Xi,规定速度为Vi。

Step2 通过上述的适应度函数，计算每个粒子适应度值Fit(Xi)。

Step3 计算每个粒子的个体最优位置pbest和全局最优位置gbest。

Step4 根据公式(21)更新粒子的速度和位置。

假设Qn为等式约束(20)的系数矩阵，r(Qn)是矩阵Qn的秩，Pn为系数矩阵Qn的阶梯型矩阵，在阶梯形矩阵中选取r(Qn)个线性无关的列，将这些列的序号集合记为(m1,m2,…,mr(Qn))，未被选中的列的序号集合记为(q1,q2,…,qn-r(Qn))，通过公式(21)来更新速度向量和位置向量部分分量的值。

vit=wvit+τ1η1(pit-xit)+τ2η2(git-xit) 。

(21)

式中：t=q1,q2,…,qn-r(Qn),xit=xit+vit，t=q1,q2,…,qn-r(Qn)。

剩下的分量值通过等式方程组求出。

Step5 对粒子的个体极值和全局极值进行更新。

Step6 若达到终止条件，即最大迭代次数，算法输出全局最佳位置，该位置就是本文的最优卸载策略，进而求出最优时延，若没有达到终止条件，则将更新后的粒子转向Step 2。

3 仿真与分析

为了验证本文所提提出的架构及卸载策略的时延性能，将所提的策略与其他几种策略进行比较。

(1)“车-边-云”协同卸载(本文卸载策略)：终端车辆卸载部分计算任务至边缘节点(固定边缘节点和移动边缘节点)和云端处理，剩余计算任务由终端车辆本地处理。

(2)“车-边”协同卸载：终端车辆仅卸载部分计算任务，由边缘节点进行计算，剩余任务由终端车辆本地处理。

(3)仅边缘节点卸载(仅边)：终端车辆卸载全部的计算任务，全部任务由边缘节点处理。

(4)仅车本地卸载(仅车)：终端车辆直接进行本地任务执行，不进行计算卸载。

最后将本文采用的改进可解等式约束的粒子群优化算法(FS-PSO)与贪婪算法(Greedy Algorithm)、遗传算法(Genetic Algorithm)进行比较。PSO算法和遗传算法都属于全局优化算法，从随机解出发，通过迭代寻找最优解，通过适应度来评价解的品质。贪心算法不是对所有问题都能得到整体最优解，但对范围相当广泛的许多问题能产生整体最优解或者是整体最优解的近似解。

3.1 仿真参数设置

表1给出了相关仿真参数设置。

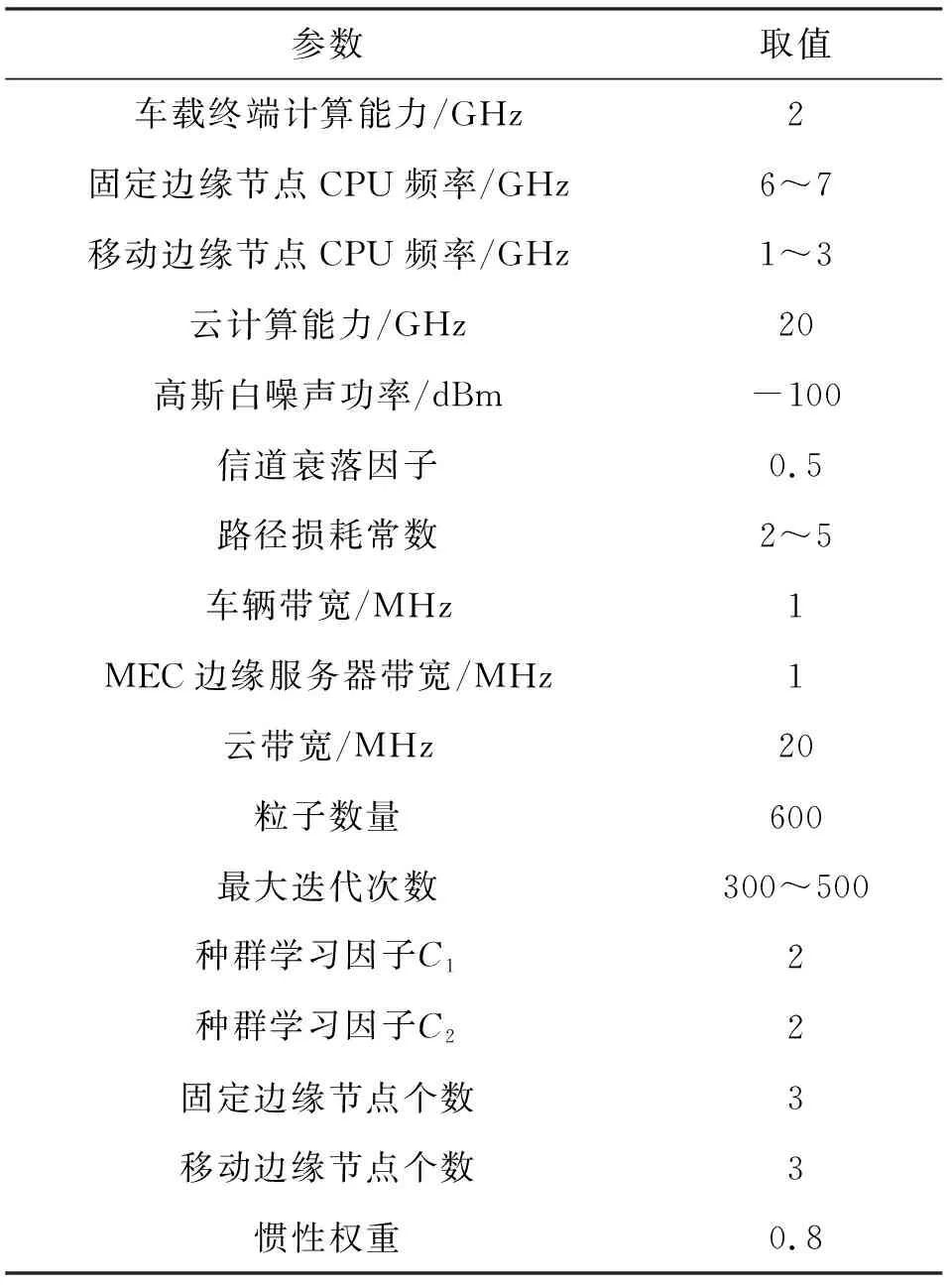
表1 相关仿真参数

3.2 仿真结果分析

图2描述了在输入数据大小影响下各策略的时延性能，假设计算复杂度为6 800 cycle/B。可以看出随着输入数据的增加。任务卸载所产生的时延也随之增加，这是因为随着数据大小的增加，计算过程中传输时延以及处理时延都会有所增加。本文采用的“车-边-云“卸载策略在时延方面明显优于其他卸载策略，与仅车辆终端计算相比减少约2.6 s。这是因为本文策略将车辆、MEC设备、云三部分资源充分调度，且云的计算资源强大，减少了处理时延。相较与其他三种策略的时延，所提出的策略时延性能分别提升了32.6%、45.3 %和88.5%。

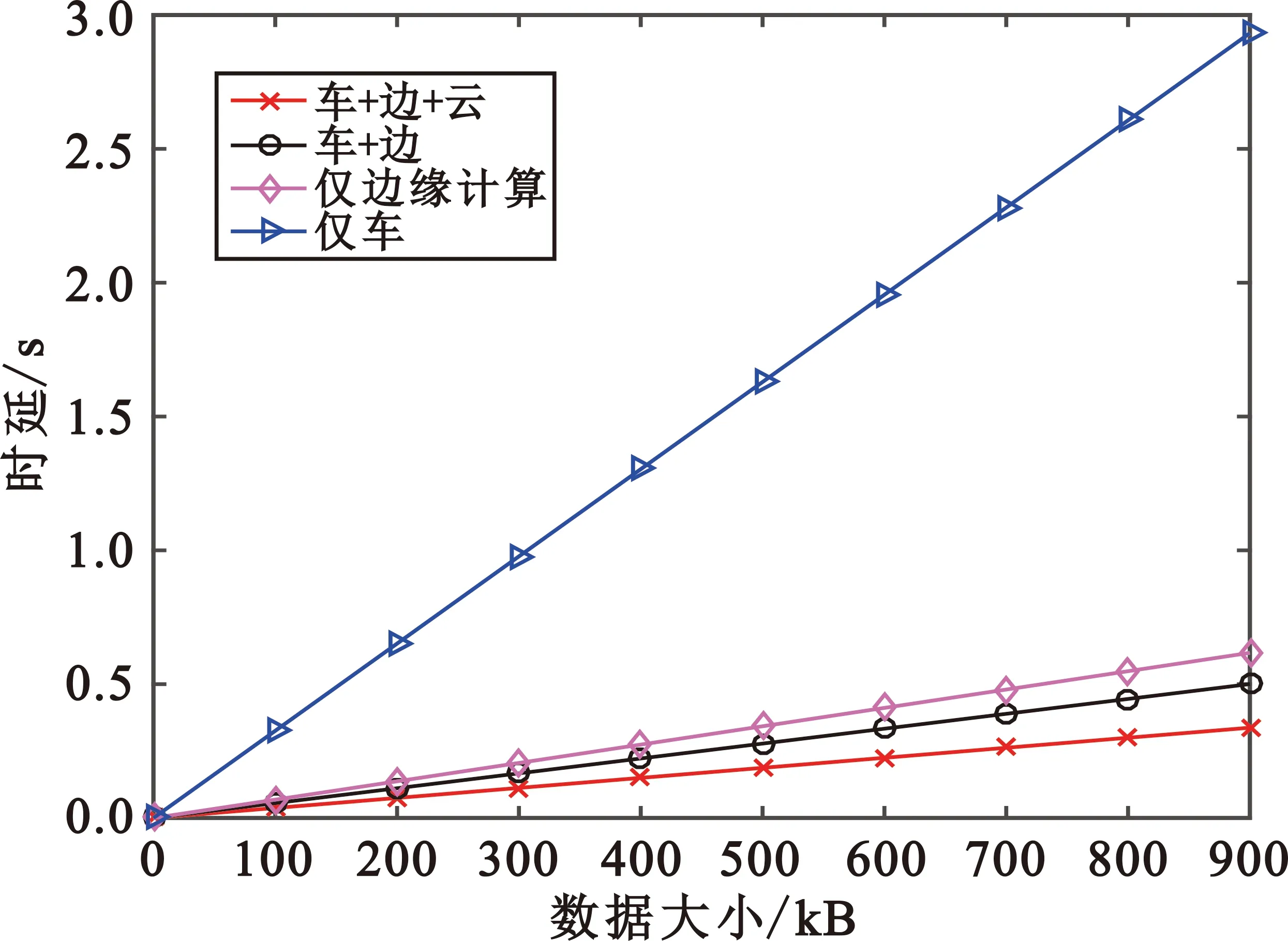
图2 不同输入数据大小各策略时延的对比

图3显示了不同复杂度下各策略时延的大小，对输入的计算任务可以有不同的处理操作，就会产生不同的计算复杂度。假设输入数据大小为580 kB，可以看出，“仅边”卸载策略在复杂度趋向于0时，仍然有一定的传输时延。这是因为卸载了全部的计算任务至边缘节点进行计算，有一定的传输时延。当计算度复杂度低于2 000 cycle/B时，“车-边-云”协同卸载策略时延高于“车-边”卸载时延和“仅边”卸载时延。这是因为计算复杂度较低时，云端处理时延所带来的时延优势不能抵消掉任务传输至云的传输时延较长问题。随着计算复杂度的增加，任务卸载的时延也随之增加，当计算复杂度超过2 000 cycle/B时，本文所提的卸载策略产生的时延是最小的。

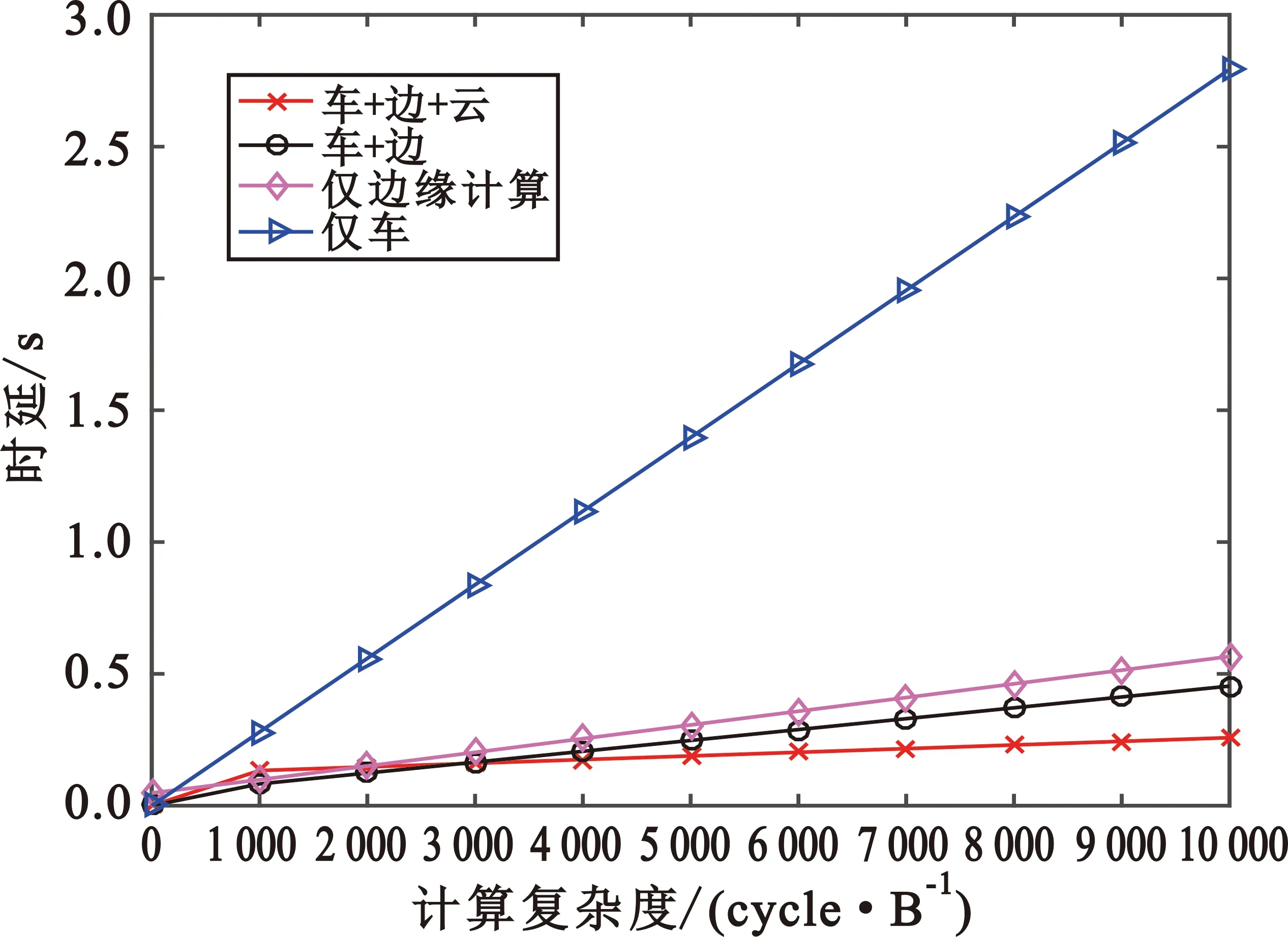
图3 不同复杂度下各策略时延的对比

图4给出了不同策略在随机计算复杂度和随机数据大小下的时延性能对比，其中，假设输入数据大小的范围为375～425 kB，CPU周期范围为1 950～2 050 Mcycle。可以看出“车-边-云”卸载策略在车辆随机任务下可以更地好降低任务完成时延，10个随机任务下几个策略的平均时延分别为0.189 s、0.252 s、0.298 s、1.306 s且与其他三种策略相比时延分别提升了21.4%、36.6%、85.5%，证明了所提策略的有效性。

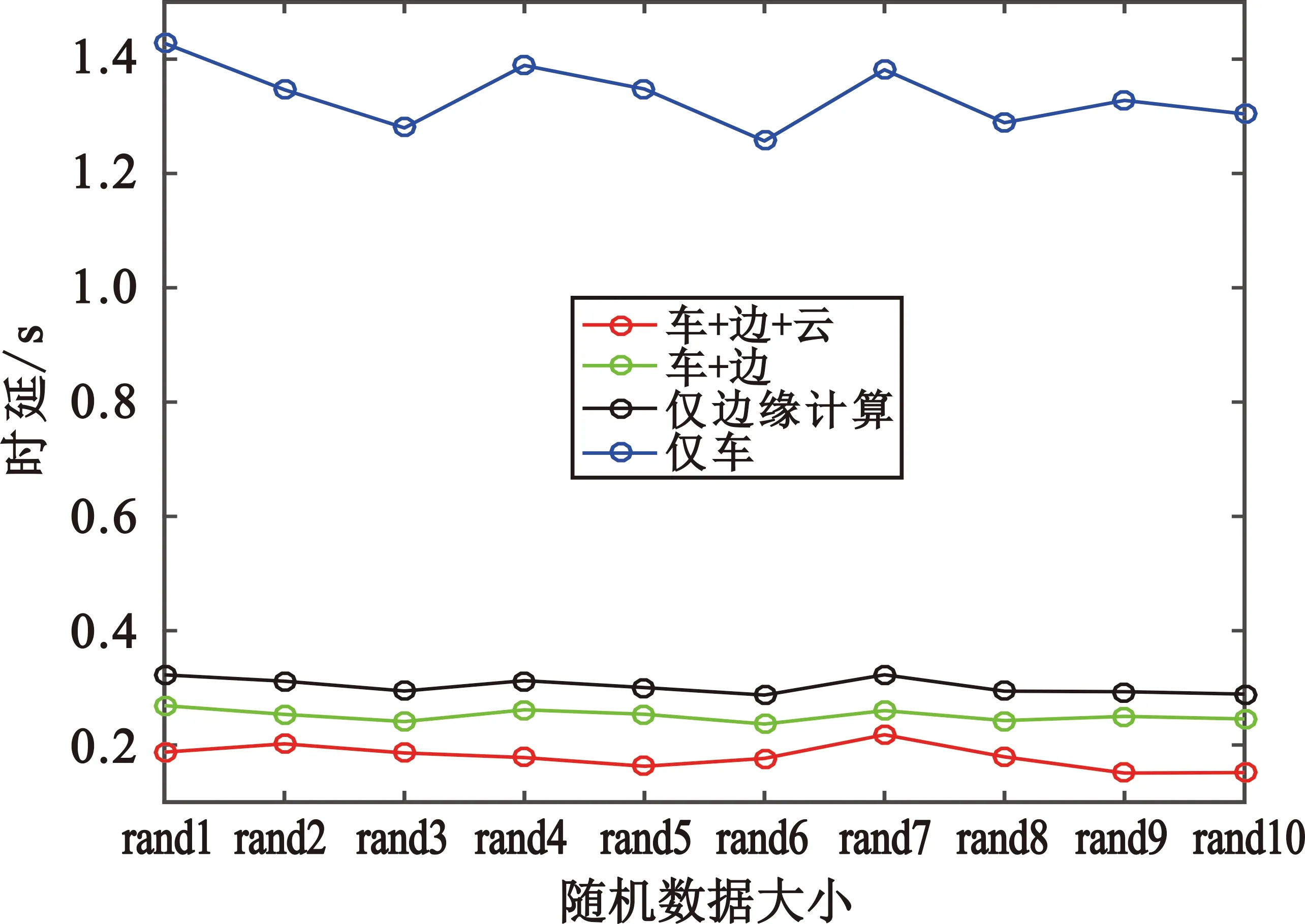
图4 随机数据大小和随机CPU周期数下的时延性能对比

图5描述了相同策略下本文的改进算法与贪婪算法和遗传算法的时延性能对比。总体来说，随着计算复杂度的增加，“车-边-云”卸载策略中基于粒子群优化算法的任务完成时间一直处于最低状态，其次是贪婪算法，时延最大的是遗传算法，这说明粒子群算法比其他两种算法能够更好地缩短用户完成时间，提高用户体验。当计算复杂度为8 000 cycle/B时，三种算法的时延分别0.216 2 s、0.296 3 s、0.339 3 s，说明粒子群优化算法对卸载任务分配更加合理。

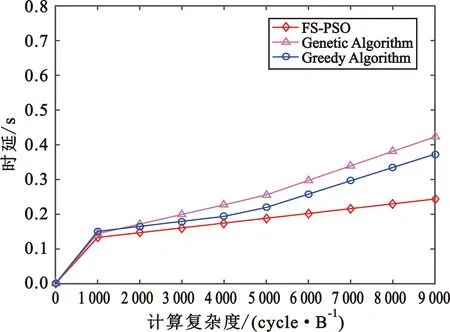
图5 相同策略下不同算法时延性能对比

4 结束语

本文提出了车联网中基于本地、边缘MEC设备和云服务器共同卸载的卸载策略，实现了车、MEC设备、云三方面的资源调度。此外，本文采用了改进的粒子群算法可解决本文时延优化问题的等式约束。数值结果表明，所提出的卸载策略可以提高任务执行效率，降低时延，实现了对车载任务的最优卸载。但本文仅考虑了单个任务，未考虑车辆任务的多样性；也仅考虑车辆在理想情况下的任务卸载，未考虑无线通信链路的不稳定性，不符合车联网的实际情形，因此后续将考虑多任务卸载以及多任务情况下任务的优先级，按任务重要度进行卸载，并研究车辆在非理想链路情况下的可靠性传输。