削减NLOS误差的UWB室内定位算法

李新春，阳士宇，张玉琛，孙鹤源

(1.辽宁工程技术大学 电子与信息工程学院，辽宁 葫芦岛 125105；2.辽宁工程技术大学 研究生院，辽宁 葫芦岛 125105)

0 引 言

UWB技术最先由美国军方提出并使用，2002年之后，美国国防部决定将超宽带通信应用到民用领域[1]。与传统的借助载波实现信号调制的通信技术不同的是，UWB技术是一种利用亚纳秒级或纳秒级窄脉冲，在理论上达到厘米级或分米级定位精度的无载波通信技术。UWB技术的时间分辨率高，抗多径能力强，安全性能优越，使其在智能仓储，工厂导航等室内定位领域被大量使用。

多径效应和NLOS环境是影响精确室内定位效果的主要因素[2]。多径效应会导致到达时间(time of arrival, TOA)估计误差的产生，而定位系统工作在NLOS环境会导致标签节点发出的电磁信号会通过散射或衍射到达定位锚节点，产生NLOS误差[3]。经典的UWB室内定位算法的抗多径能力强，但在受NLOS误差影响时会产生较大的定位误差，故研究削减NLOS误差的算法成为了当下热点之一。文献[4]提出一种基于NLOS误差先验信息的定位算法，提高了NLOS环境下的定位精度，但NLOS先验信息的获取需要采集大量的数据；文献[5]提出一种改进的扩展卡尔曼滤波算法，通过阈值判断后改变增益系数的方法抑制了NLOS误差，但对NLOS误差的削减不彻底；文献[6]提出一种Chan-Taylor混合算法，合理地利用了Chan算法与Taylor级数展开法的优势，用Chan算法估计出的标签节点的坐标作为Taylor级数展开法迭代的初始位置来精确估计标签节点的位置，但初次估计中没有被削除的NLOS误差也会被带入Taylor迭代过程，导致结果误差增大；文献[7]利用自适应卡尔曼滤波算法对移动标签节点周围变化的环境实时更新，提高了定位精度，但NLOS环境下卡尔曼滤波算法定位误差较大的缺点还是没有解决；文献[8]提出一种探索型多目标粒子群优化算法(Exploratory multi-objective particle swarm optimization，EMOPSO)，在保留传统PSO算法收敛性的基础上，提高了定位精度，但在NLOS环境下存在复杂度过高的问题。

针对以上问题，本文提出了一种基于TDOA值来判别与削减NLOS误差的卡尔曼滤波算法。具体分为以下3步：1)利用传统卡尔曼滤波算法初次估计移动标签节点并根据结果计算得到带有误差的TDOA值；2)基于TDOA差值进行NLOS误差判别，根据环境判别结果进行视距重构，削减NLOS误差，同时，利用仅受LOS误差影响的历史值更新卡尔曼滤波协方差阵，消除环境误差带来的影响；3)将上一步削减误差后的结果代入Chan-Taylor算法迭代计算，得到最终精确的定位结果。实验结果表明，该算法能提高在NLOS环境下的定位精度。

1 UWB室内定位方法

UWB室内定位是利用电参量信息，例如飞行时间、相位等来实现对未知标签节点的定位，根据测量信号的不同的特征参数分为基于信号到达角度(angle of arrival, AOA)、基于接收信号强度(received signal strength indication, RSSI)、基于TOA与基于TDOA的定位方法[9-10]。其中，基于TDOA的定位可以通过分时复用机制来避免多址干扰对定位效果带来的影响，故成为了最适合UWB室内定位的方法。

基于TDOA的定位方法是通过测量标签节点发出的信号到达任意两个锚节点的时间差，得出未知坐标的标签节点同这两个锚节点间的TDOA值[11]。由于现实中所有锚节点与同一台计算机主机相连，故认为锚节点之间时间完全同步，进而可以通过求出的TDOA值绘制出以这两个锚节点为焦点的双曲线图，如图1所示。

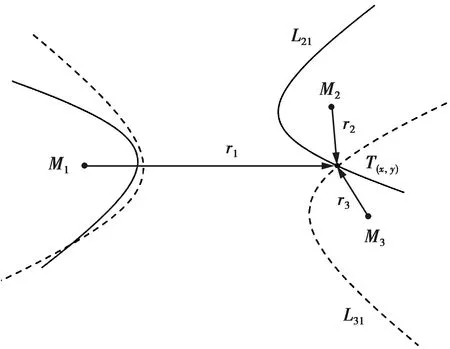
图1 基于TDOA的定位原理图Fig.1 Location schematic diagram based on TDOA

假设在定位区域内放置n个参与定位的锚节点，以锚节点i(xi,yi)和锚节点1(x1,y1)为焦点组成一个双曲线组(Mi,M1)，i=2,…,n。在标签节点开始发送信号后，可以计算出它们所接收到信号的时间差ti,1，表示为

(1)

(1)式中：ri表示锚节点i和标签节点的距离；ri,1表示锚节点i和锚节点1与标签节点之间的距离差；c为信号电磁波传播的速度。

根据(1)式可以得到以(Mi,M1)为焦点的双曲线Li,1的方程为

(2)

得到至少两组双曲线组的到达时间差后，就可以根据(2)式构建如(3)式所示的方程组。通过求解此方程组就能够得出标签节点的坐标。

(3)

2 NLOS误差

在复杂环境下，UWB室内定位的计算结果往往受多径效应、NLOS环境等因素的影响，产生误差[12]。若ri,1表示第i个锚节点和第1个锚节点与标签节点间的距离差，则ri,1等于真实距离差Li,1与标准测量误差ni和NLOS误差ei之和，即

ri,1=Li,1+ni+ei

(4)

标准测量误差ni由LOS环境中多径效应等因素造成的误差构成，被认为服从均值和标准差为μ和σ的高斯分布，表示为

(5)

而NLOS误差ei通常被认为服从信道环境决定的超量时延τ的指数分布，表示为

(6)

多径效应是由于各种散射物体和反射物体的存在，导致传输过程中的路径存在不同时延；在UWB信号发射后，各多径分量到达UWB接收端的时间不相同，导致相互叠加，出现失真，产生误差。而非视距传播则是当UWB定位系统工作在NLOS环境时，UWB信号穿透阻挡物时会产生时延，产生NLOS误差。经典的UWB室内定位算法抗多径能力强，能有效地减小由多径效应引起的定位误差，故削减NLOS误差成为了研究的一个关键。

3 定位算法

在移动标签节点受NLOS误差影响时，Chan算法，Taylor级数展开法，传统卡尔曼滤波算法等经典UWB室内定位算法会出现定位误差较大，定位精度不高的问题[13-14]。目前常用的削减NLOS误差的方法有视距重构、统计校正和消极加权等[15]。本文提出一种基于TDOA差值进行视距重构的卡尔曼滤波算法，利用视距重构削减卡尔曼滤波迭代过程中的NLOS误差，提高定位精度，如图2所示。

图2 定位算法流程图Fig.2 Flowchart of positioning algorithm

定位算法的具体步骤如下。

1)卡尔曼滤波算法初次估计。卡尔曼滤波算法在对动态目标定位中有广泛的应用，能够高效地估计移动标签节点的状态。传统的卡尔曼滤波分为预测和更新两个阶段[16-17]。在预测阶段，算法通过使用上一状态的估计，对当前状态进行估计。而在更新阶段，利用当前状态的观测值优化在预测阶段获得的预测值，获得一个更精确的新估计值。

状态方程为

Xn=AXn-1+Bμn-1+Fn,n-1wn-1

(7)

测量方程为

Yn=HnXn+vn

(8)

(7)—(8)式中：Xn，Yn分别为状态向量和观测向量；A为状态转移矩阵；B为可选的控制输入μ的增益；Fn,n-1为状态噪声系数矩阵；wn-1为状态噪声序列；vn为观测噪声序列；Hn为观测向量系数矩阵。

状态方程和测量方程将第n时刻的观测值、状态值与观测值的历史信息之间联系起来。因此，只需要一个初始状态向量值和一个估计误差的协方差，就可以通过迭代估计出相对应时间节点上的状态值。

2)基于TDOA差值的视距重构。根据(7)—(8)式求出卡尔曼滤波迭代的状态方程为

(9)

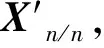
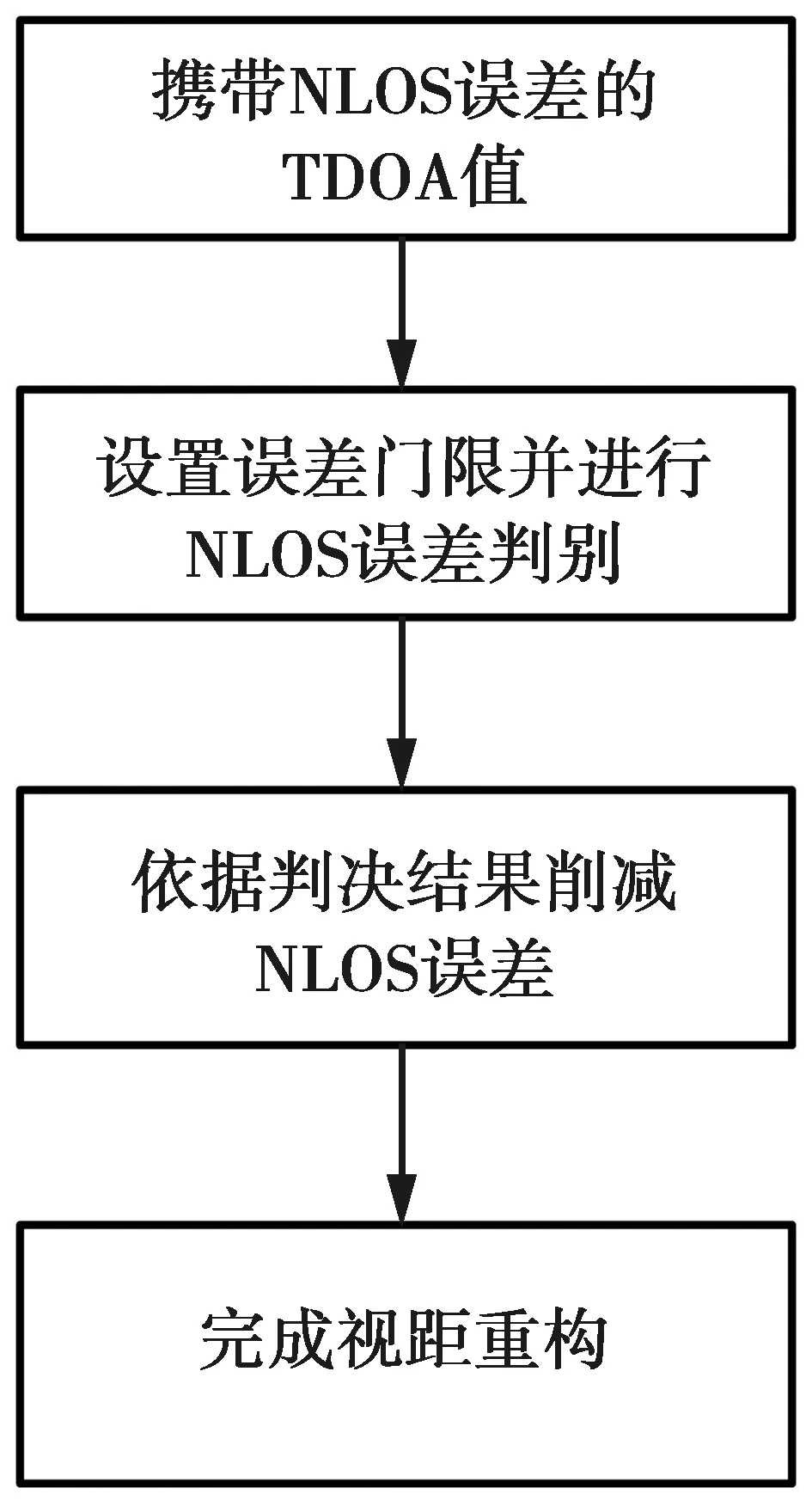
图3 视距重构流程图Fig.3 Flowchart of LOS reconstruction

(10)

若判断出存在NLOS误差，则更新迭代公式。迭代公式为

(11)

(11)式中：E为单位矩阵；e为单位向量。(11)式与(9)式相比，非零增益εn/n-1的作用会避免NLOS误差进入下一次状态向量的迭代计算，完成视距重构。这种视距重构的方法不需要NLOS先验信息或超量时延等复杂信息，仅需计算容易获取的TDOA值便可以实现对NLOS误差的判别与削减，复杂度低。

若判断仅存在LOS误差，则更新协方差阵。协方差阵为

(12)

3)Chan-Taylor算法迭代计算。Chan算法在仅存在LOS误差的情况下有较高的定位精度，而Taylor级数展开算法作为一种迭代算法，通过合理设置初始位置坐标可以有效地降低定位误差[19]。故将上一步卡尔曼滤波算法的结果先代入Chan算法估计，将Chan算法的估计结果作为Taylor级数展开法的初始值进行迭代，可以同时合理利用两种算法的优点。

由(3)式和(11)—(12)式可得

(13)

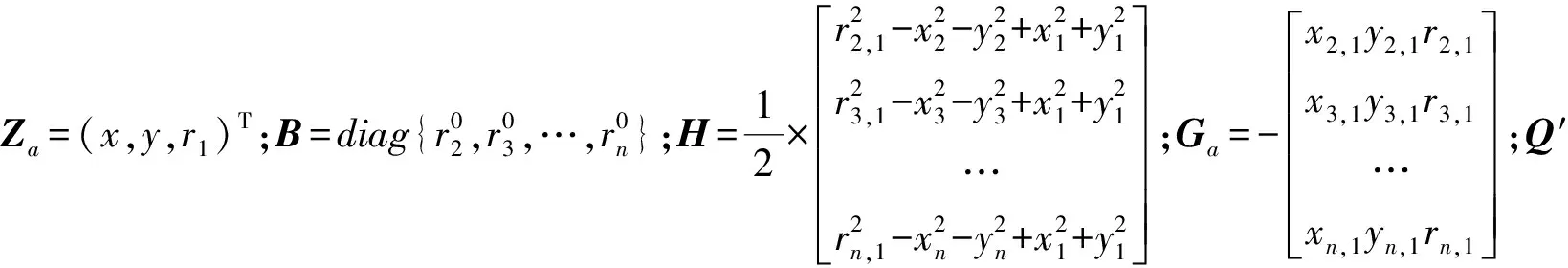
由于ψ未知，所以在估计时用Q近似代替ψ。可得加权最小二乘法(weighted least squares, WLS)估计值为

(14)

(14)式中，第一次通过WLS计算的估计值Za是在预设x、y、r1三者相互独立的情况下得到的。而在实际应用中，x、y、r1往往是相关的，而且用Q近似代替ψ也会导致误差产生，影响定位精度。于是引入Chan算法，将求非线性方程组解的问题变为非线性的最优化问题，利用初次WLS的结果重新构建误差方程组再次进行WLS估计，即

(15)

(15)式中，B2=diag{xa-x1,ya-y1,ra}。利用第一次估计值Za可以近似估计B2，据此进行第二次WLS估计，即

(16)

第二次WLS估计值Za2与第一次WLS估计Za相比，利用了多锚节的冗余信息二次加权估计，并且消除了由于近似替代产生的误差，提高了估计结果的精度。

ψ=h-Gδ

(17)

用最小二乘法求解δ可得本次迭代后的标签节点位置坐标为

(18)

|Δx+Δy|<η

(19)

4 实验与分析

4个UWB定位模块作为锚节点，放置于边长为8 m的室内正方形场地角落；位于场地中心的个人计算机作为主锚节点，用于汇集锚节点采集的定位数据。实验中设置卡尔曼滤波算法的初始矩阵系数为10，A=[1,0.5;0,1]，Hn=[1,0;0,0]，误差门限值λ为0.55 m(λ为本次实验的LOS环境下预先测得的标准测量误差值)。选用累计分布函数(cumulative distribution function，CDF)均方根误差(root mean squared error，RMSE)与运行时间作为评价算法定位性能的指标。

CDF被用来表示随机变量分布设定区间的概率，能直观地描述定位误差出现在设定区间的概率；RMSE能很好反映数据的变化程度，值越小表示估计值与测量值之间的偏差越小，具有更强的稳定性；运行时间是当锚节点采集的一组数据返回主锚节点后，算法处理数据的时间，一般被用来衡量算法的时间复杂度。

4.1 移动标签节点仅受LOS环境影响

图4为LOS实验环境示意图。图4中，UWB标签节点按照标定的轨迹(边长为6 m的正方形轨迹)以0.5 m/s的速度移动(标签节点移动起点为左下角)，采样时间间隔为0.5 s。

图4 LOS环境实验示意图Fig.4 Schematic diagram of LOS environment experiment

实验结果如图5所示。从图5可以看出，各算法在LOS环境下的定位误差都较小，能达到分米级的定位精度。本文算法利用仅受LOS误差影响的历史值更新卡尔曼滤波过程的协方差阵，且合理利用Taylor级数展开法进行迭代，因此，与传统卡尔曼滤波算法、Chan-Taylor混合算法等相比，本文算法定位误差更小。

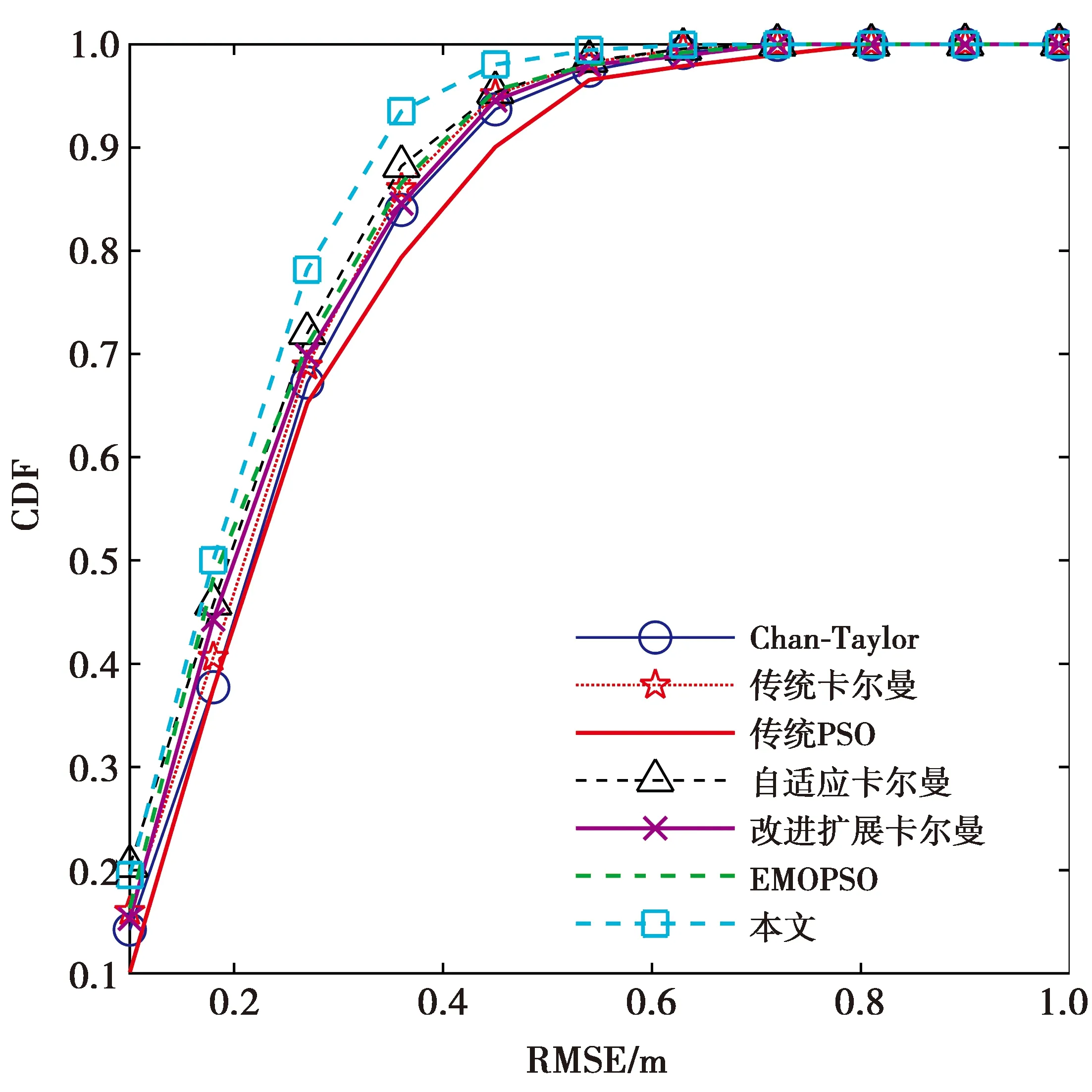
图5 LOS环境下CDF分布图Fig.5 CDF distribution map in LOS environment

4.2 移动标签节点受NLOS环境影响

图6为NLOS实验环境示意图。图6中，UWB标签节点按照标定的轨迹(边长为6 m的正方形轨迹)以0.5 m/s的速度移动(标签节点移动起点为左下角)，采样时间间隔为0.5 s，障碍物为厚度约25 cm的墙柱。当移动标签节点被墙柱遮挡时，会受到NLOS误差的影响。

实验结果如图7与表1所示。由表1可见，Chan-Taylor混合算法、传统卡尔曼滤波算法与传统PSO算法在移动标签节点受NLOS环境影响时定位误差较大，定位效果不佳；自适应卡尔曼算法定位精度比前三者高，但削减NLOS误差不彻底；改进扩展卡尔曼滤波算法能削减部分NLOS误差，但算法复杂度较高；EMOPSO算法在NLOS环境下的复杂度过高，不利于实际环境中的实时室内定位；而本文算法利用了基于TDOA差值的视距重构过程，削减NLOS误差的效果优于自适应卡尔曼滤波算法与改进扩展卡尔曼算法，RMSE值约为0.28 m，最大定位误差约为0.59 m，在低复杂度的情况下具有更高的定位精度且稳定性更强。图7对比了定位效果较为良好的几种算法。从图7可以看出，本文算法处理后的移动标签节点运动轨迹更贴近于标定轨迹且未出现断点。

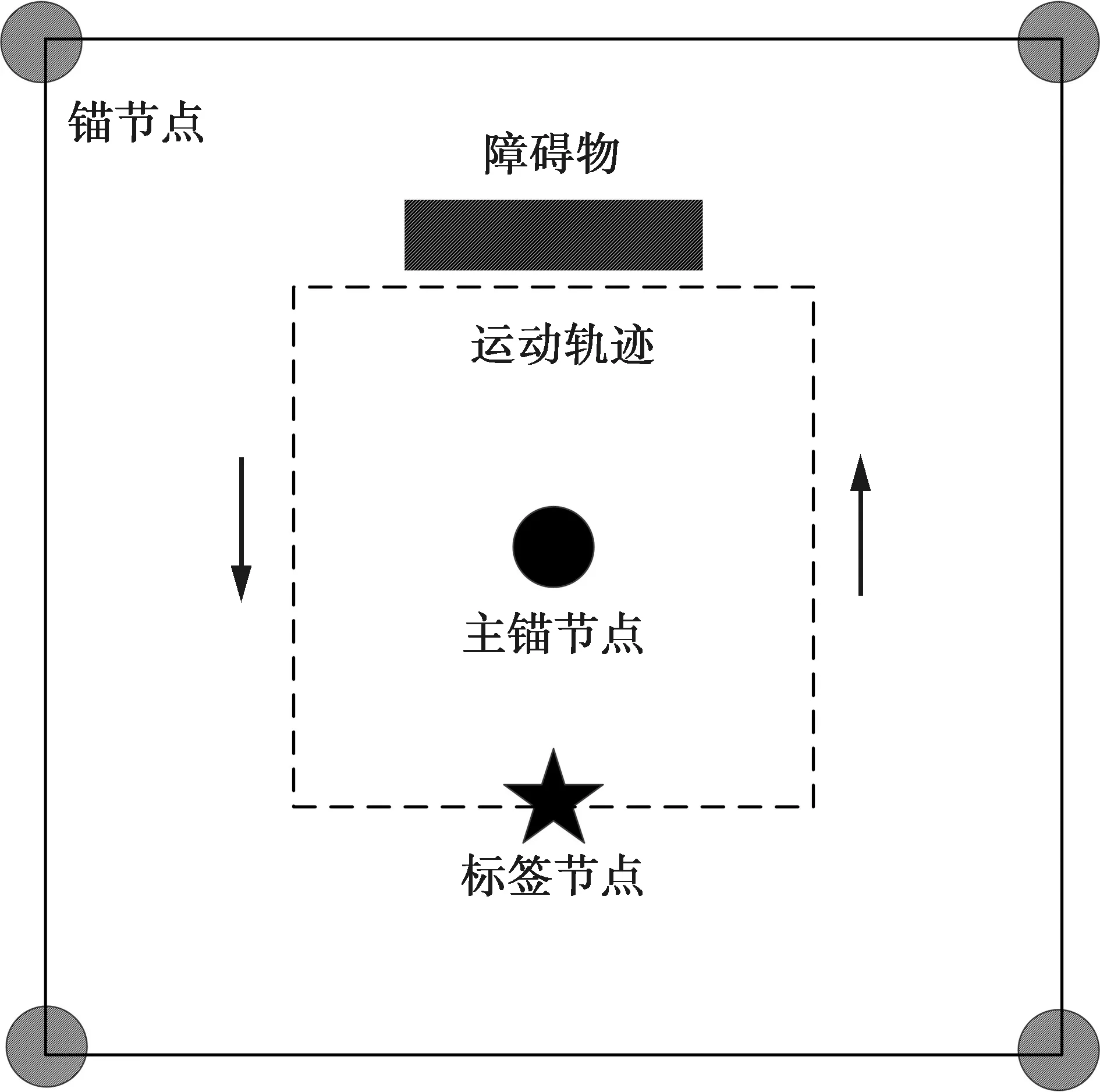
图6 NLOS环境实验示意图Fig.6 Schematic diagram of NLOS environment experiment

图7 NLOS环境定位轨迹图Fig.7 Track of NLOS environment location

表1 NLOS环境下各算法比较Tab.1 Comparison of different algorithms in NLOS environment

5 结 论

本文提出了一种基于TDOA差值判别并削减NLOS误差的UWB室内定位算法。该算法结合了卡尔曼滤波能优化更新预测方程的方法减小定位误差与Chan-Taylor定位算法迭代精度高的优点。通过基于TDOA差值的NLOS误差判别方法，在不需要获取NLOS先验信息等复杂参数的条件下完成视距重构，削减NLOS误差，并利用仅受LOS误差影响的历史值更新卡尔曼滤波协方差阵，减小环境变化带来的误差影响，利用Chan-Taylor算法进行迭代，得到精确的定位结果。通过实验验证，在NLOS环境下，该算法时间复杂度低，能有效减小定位误差、提高定位精度，稳定性更强。