基于DynamicRank的重要节点集挖掘算法

朱 华，潘 侃，王 磊，陈端兵,3

(1.云南电网有限责任公司电力科学研究院 昆明 650217；2.成都数之联科技股份有限公司 成都 610041；3.电子科技大学大数据研究中心 成都 611731)

0 引 言

现实生活中，很多复杂系统如社交、城市交通等网络，都可以用图表示。这些网络中，社交网络里的官方账号、城市交通网络里的交通枢纽等少数节点对信息扩散起到了关键作用[1]。提早发现这类关键节点，一方面，可利用其高影响力加速信息传播，如产品推广信息的传播；另一方面，也能有效地监控和预防现实生活中可能出现的各种突发状况，如社交网络中的谣言传播、交通网络中重要路口堵塞导致交通系统瘫痪等。单个关键节点的影响力是有限的，一组关键节点在相互促进下会造成更为广泛的影响。因此，找到重要传播源(种子节点集)对信息传播与控制具有重要作用。

在复杂网络中识别一组有影响力的传播者，有一种简单的方法是依据节点重要性排序结果[2-3]选择top-K节点作为初始传播源(种子集)。目前已有很多节点重要性排序算法，归纳起来可分为两类。一类是基于结构特征的指标和方法，通过捕捉节点之间的局部连边信息或路径信息，衡量节点的重要性，例如度中心性(Degree)、K-shell中心性[4]和H-index[5]中心性；另外一类是基于路径和全局随机游走的方法[6-8]，利用整个图的拓扑信息挖掘重要节点。在不考虑时间开销的前提下，从初始节点出发将信息传播出去，当随机游走趋于稳定时，信息保留越多的节点就越重要。

文献[9]将复杂网络中一组重要节点识别问题定义为影响力最大化问题，提出了独立级联(independent cascade，IC)模型和线性阈值(linear threshold，LT)模型两种求解方法。IC模型假定传播激活的独立性，每个活跃的节点以一定概率激活其不活跃的邻居，而不受其他活跃节点的影响。LT模型考虑邻居的联合激活，如果一个非活动节点的活跃邻居的权重之和超过给定阈值，该节点将被激活。

IC模型利用传统重要节点排序方法挖掘重要节点集，只考虑每个节点独立的影响力。但是，在影响力传播过程中，节点集内的节点存在相互促进和补充的关系，考虑节点集内部关系的方法更符合实际。因此，本文基于DynamicRank[10]方法的单节点影响力概率计算模型，提出了多种子节点的级联传播概率计算方法，以捕捉种子集内部对信息传播的积极促进影响。同时，大多数贪心策略都存在一个问题，即某些传播者距离太近，以至于它们的影响可能重叠。因此，在DynamicRank概率排序模型基础上，本文改进纯粹贪心迭代策略，降低种子集里重叠邻居对影响力传播带来的消极影响，优先从种子节点邻居以外的节点中选择候选节点。通过考虑种子集内部各节点之间相互促进和抑制2个方面的影响，挖掘出更高影响力的种子集。相较于目前应用较多的基于重要节点排序方法(K-shell[4]，Degree，H-index[5]，DynamicRank[10])和重要节点集挖掘方法(VoteRank[11]，EnRenew[12])，本文提出的方法能更准确、更有效地识别复杂网络中高影响力节点集。在4个实际网络上的实验表明，本文方法选出的节点集具有更好的信息扩散能力，在Grid数据集上，相较于其他基准方法，本文方法的传播范围平均提升了49.3%。

1 相关工作

针对影响力最大化问题，研究者提出了各种启发式算法。例如，文献[13]提出了一种基于IC模型的Degree-discount启发式方法。其基本思想是，在计算种子集影响力时，如果节点v的邻居节点u被选为种子节点，由于两者的影响力存在重叠，则需要对节点v的度数进行度量折扣。文献[14]考虑弱连接因素，提出了一种通过将最大化问题映射为最优渗滤问题的集体优化方法。

采用贪心算法求解影响力最大化问题也是主流研究方向之一，其核心是在每次迭代中选择当前影响力最大的节点集。在不降低精度的情况下，文献[15]设计了一种改进的贪心策略，利用目标函数的子模数，将计算代价降低了两个数量级。文献[16]平衡了精度和时间复杂度，设计了一种离散的贪心求解算法，利用本地网络拓扑结构信息，有效识别最大影响力的节点集。文献[11]提出了一种简单有效的组节点选择方法VoteRank，它通过投票策略选择最有影响力的节点集。VoteRank使用迭代选择策略，充分利用了节点的局部信息但忽略了边的信息。文献[17]在此基础上提出了WvoteRank以提升在带权图中重要节点集挖掘的准确性。文献[12]进一步利用节点间的差异，提出了一种基于节点信息熵的启发式算法EnRenew以选择一组高影响力的节点。在信息传播概率函数的帮助下，文献[18]根据所选节点的局部路径降低其他节点的得分，提出了一种基于重排序的方法Re-Rank来挖掘一组重要节点集。

2 基于DynamicRank的重要节点集挖掘方法

本文研究主要针对无向无权图G(V,E)。其中，V={v1,v2,…,vn}是节点集合，E={e1,e2,…,em}是边集合，n和m分别是节点数量和边数量，直接与节点v相连的一阶邻居记为Γ1(v)。为了方便描述，拓展邻居的定义如下。

定义1高阶邻居。若v是节点y的一阶邻居，节点y属于节点u的i-1阶邻居Γi-1(u)，那么节点u的i阶邻居定义为

Γi(u)={v|v∈Γ1(y),y∈Γi-1(u),

v∉Γi-1(u),v∉Γi-2(u)}

(1)

定义2节点集的高阶邻居。节点集S的i阶邻居Γi(S)定义为

(2)

2.1 DynamicRank节点重要性排序方法

DynamicRank算法利用概率传播模型，信息以中心节点为初始传播源向外传播，在i阶邻域内的所有节点的感染概率之和反映了该中心节点的影响力。概率传播模型中，节点信息往往都是从低阶邻居向高阶邻居传播。对于一个无向无权图G(V,E)，假设节点u为初始感染节点，x是节点u的i-1阶邻居，y是节点u的i阶邻居。当节点x与y直接相连时，节点y将以β的概率被x感染。节点y被x感染的概率为p+(y|x)=βp+(x)。因此，在初始节点u的影响下，i阶邻居y不被感染的概率为

(3)

节点y被感染的概率为

p+(y|u)=1-p-(y|u)

(4)

(3)—(4)式中，中心节点是u，其初始感染概率为p+(u)=1。

从一个中心节点u出发，在给定邻域范围(本文取3阶邻域)下，中心节点u的影响力为u的3阶以内邻居被感染的概率之和，计算公式为

(5)

2.2 基于DynamicRank的重要节点集纯粹贪心选择策略

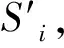
贪心选择的核心就是计算节点集的影响力，而一组节点的影响力是由种子集中多个节点共同决定的。若当前的节点集为S，邻域内节点y受到节点集S影响而被感染的概率为

(6)

基于此，节点集S的影响力可以定义为

(7)

2.3 重要节点集选择的增强贪心性选择策略

当一个节点u被选为信息的传播源时，如果u附近的节点v1再次被选为传播源，那么传播范围增益很小。因此，最好选择相距较远的节点v2，以尽可能多地影响周围的节点，如图1所示。也就是说，在一个节点被选为传播源后，它的邻居和邻居的邻居被选为传播源的概率应该降低，因此，在每次迭代过程中，从种子集邻居以外的节点集选择候选节点，更为合理科学。

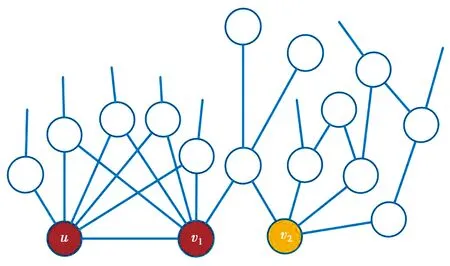
图1 具有重叠邻居的种子集选择策略示意图Fig.1 Illustration of seeds selection strategy with overlapping neighbors

在利用纯粹贪心策略选择候选节点时，可能会选择到种子集S的一阶邻居节点，由于邻居节点u与种子节点直接相连，u有很大概率被种子节点感染，选取u作为种子节点意义不大。因此，在纯粹贪心基础上，提出一种增强的贪心选择策略。候选节点优先从种子集邻居以外的节点集V-Γ1(S)中选择。特别地，当图中所有节点都是S的邻居即V-Γ1(S)=Φ时，从图中去除当前种子集的节点及其连边得到新的图G′。然后，从G′中按上述策略挑选重要节点加入种子集，具体步骤如下。

1)给定种子集规模M，根据DynamicRank排序算法计算所有节点的重要性分数，选取分值最高的节点vmax加入种子集S={vmax}。

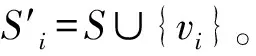
4)若|S|=M，输出最终的种子集S，结束。否则，若V-Γ1(S)≠Φ，直接返回步骤2继续执行；若V-Γ1(S)=Φ，则在图中去除种子集S中的节点及其连边，再返回步骤2)继续执行。

图2为纯粹贪心与增强贪心的重要节点集选择对比的示意图。为了说明增强贪心算法的优势，对图2中的网络分别用纯粹贪心和增强贪心两种策略选择规模M=5的重要节点集。两种方法都利用DynamicRank选出影响力最高的节点v14作为初始的种子集。经过5次迭代选择，纯粹贪心策略选出的种子集为S1={14,8,12,22,1}，有4个节点在社区1，1个节点在社区2，信息从这组节点出发很难传播到社区3，实际上，以这组节点为初始感染节点，用SIR传播模型仿真得到的传播规模为11.892(计算方法见3.1)。而采用增强贪心选择策略选出的种子集为S2={14,8,22,9,27}，种子节点分散在3个社区中，以S2为初始感染节点，用SIR传播模型仿真得到的传播规模为12.362。显然，增强的贪心策略能挖掘出影响力更大的种子集。

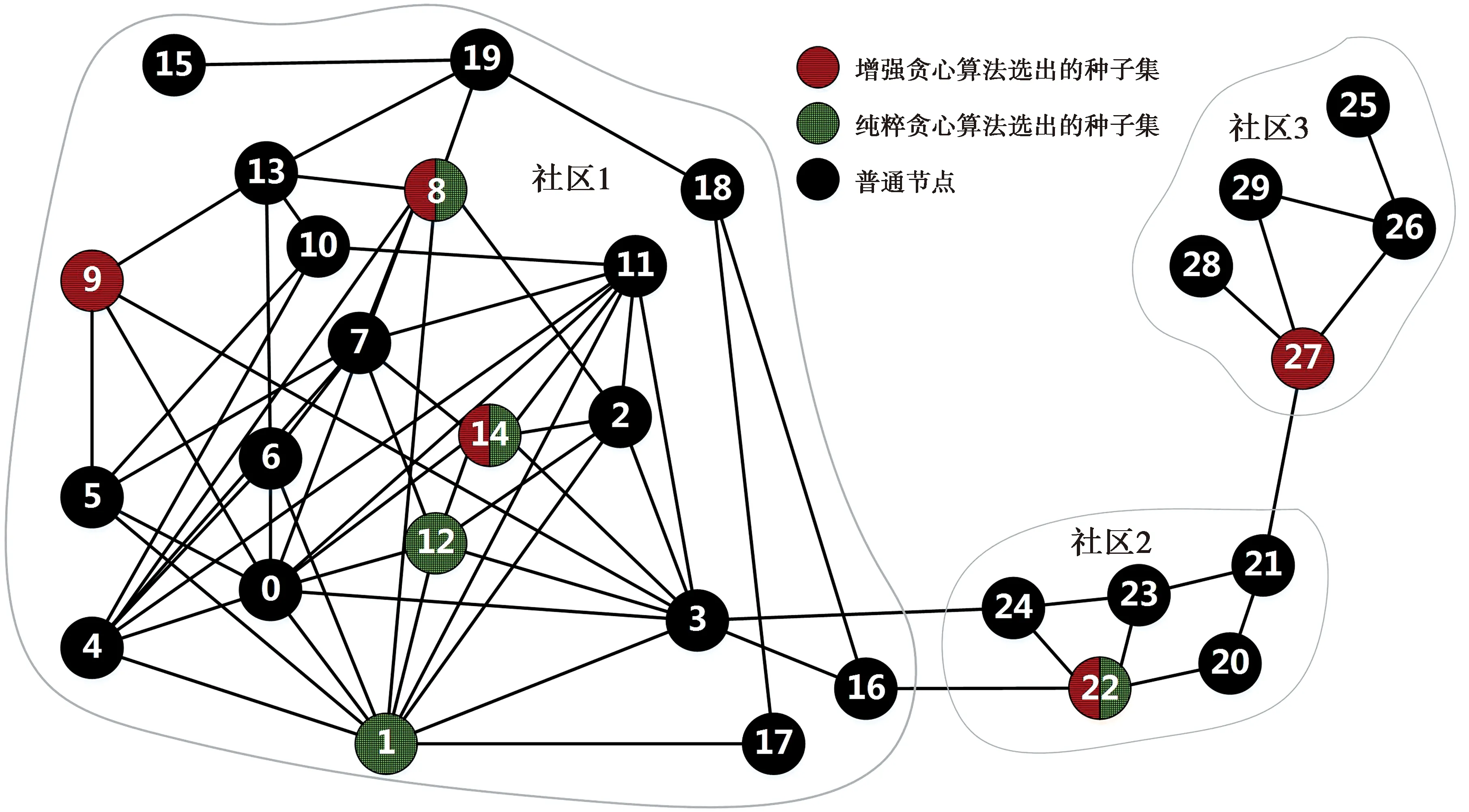
图2 纯粹贪心与增强贪心的重要节点集选择对比Fig.2 Comparison of important node set selection for pure greedy and enhanced greedy strategies

3 实验与讨论

论文利用4个真实网络对提出的方法进行了测试，并和已有的重要节点挖掘方法进行了对比分析，包括度中心性(Degree)、 K-shell中心性[4]、H-index中心性[5]、DynamicRank[10]以及重要节点集挖掘方法VoteRank[11]和 EnRenew[12]。另外，本文方法也和度中心性与K-shell中心性方法的改进版本Degree_non和K-shell_non进行了对比，即：当选择一个节点作为种子节点后，它的邻居将不会再选为种子节点[11]。

3.1 传播模型与评估方法

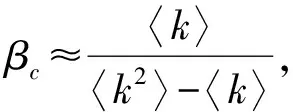
(8)

(8)式中：tc是传播达到稳态的时间；nR(tc)是传播到稳态时的康复节点数目；n是网络节点总数。

3.2 数据集

本文选择了4个真实网络进行测试和对比。4个网络包括：Email[20]，是Rovirai Virgili大学成员之间的电子邮件交换网络；Grid[21]，是美国西部的某电力网络；Yeast[22]，是酵母中的蛋白质相互作用的无向网络；Vidal[23]，是表示人类蛋白质相互作用的网络。这4个真实网络的基本结构特征如表1所示。表1中：n是节点数目；m是边数目；〈k〉表示所有节点的平均度；kmax代表节点的最大度；〈c〉为所有节点的平均聚集系数。

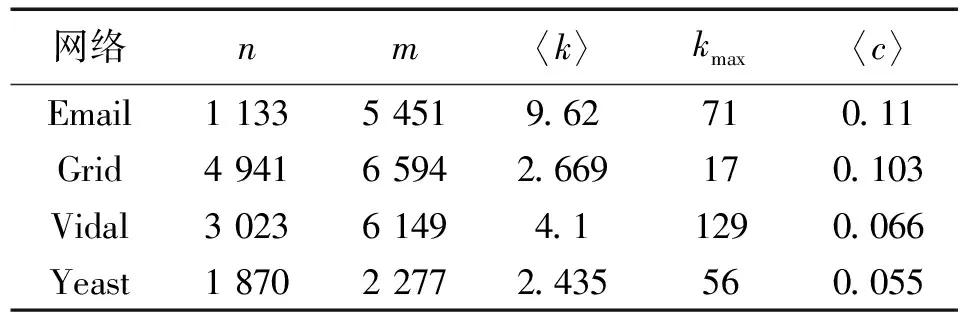
表1 真实网络基本结构特征数据Tab.1 Basic structuralproperties of real networks

3.3 实验及分析

为了比较各个重要节点挖掘方法的效果，本文实验对不同重要节点挖掘算法的种子集进行了500次SIR传播仿真实验，并将500次的平均F(tc)值作为该种子集的影响力。实验中设置DynamicRank模型的传播概率和SIR仿真中的传染概率均为β=1.2βc。表2显示了不同重要节点挖掘算法所得种子集的平均传播规模。相比于已有的基于重要节点排序的重要节点集挖掘方法Degree、Degree_non、K-shell、 K-shell_non、H-index、DynamicRank，基于投票策略的VoteRank方法，以及基于节点信息熵的EnRenew方法，本文提出的方法在4个数据集上都取得了最好的结果。特别地，在Grid数据集上，本论文所提方法的影响规模明显高于现有的重要节点集挖掘算法，传播范围较上述算法平均提升了49.3%。本文方法挖掘出的种子节点集影响的节点规模可达到0.121，比较有竞争力的VoteRank、EnRenew、Degree_non的影响规模分别为0.113、0.101、0.112。3种方法平均影响规模为0.108，本文方法选出的重要节点集其影响规模提升了11.7%；同时，直接基于DynamicRank方法排序结果选出的种子集，其传播规模只有0.065，本文利用级联概率计算和增强贪心策略优化后，挖掘出的种子集的传播规模大幅度提升了86%。这说明，改进DynamicRank中的独立传染概率的级联概率计算方法能更加有效地衡量种子集的影响力，在贪心选择过程中能挖掘出更高影响力的种子集。

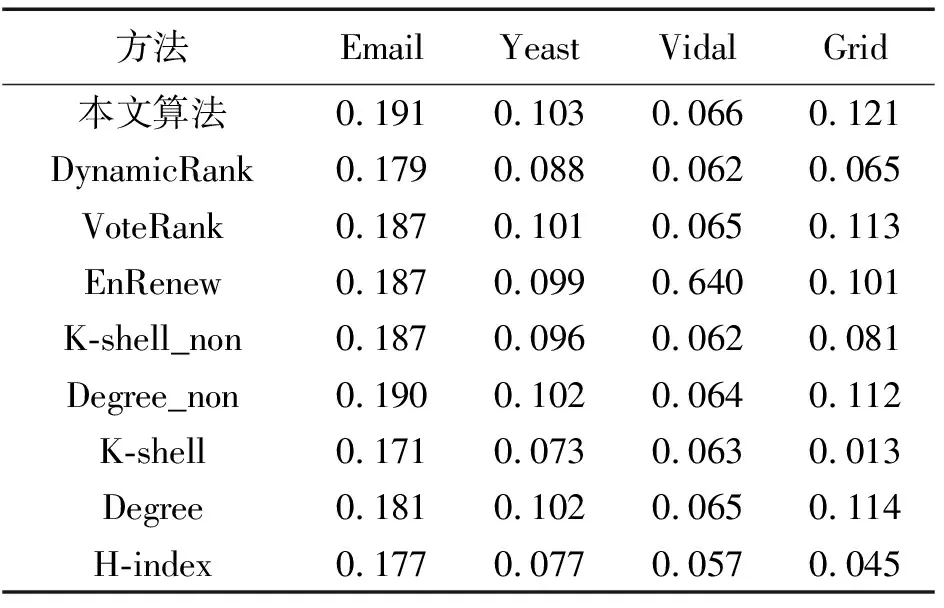
表2 SIR模型仿真结果F(tc)Tab.2 Simulation results F(tc) according to SIR model

图3为不同种子集规模下不同算法的性能对比。由图3可见，在不同种子集规模下，相对于现有的重要节点集挖掘算法，本文提出的方法取得了更好的结果。在大部分情况下，本文提出的方法都取得了最好的效果。当规模逐渐变大时，VoteRank和Degree_non等方法与本文方法相当，都能挖掘出图中影响力较大的关键节点集。

为了验证本文学习模型的鲁棒性，对比分析各方法在不同感染概率下的传播规模，如图4所示。感染概率β=cβc，随着系数c的增长，感染概率β相应增加。由图4可见，在4个网络中，种子集的影响力随着系数c的增加而不断扩大。K-shell、DynamicRank和H-index方法的增长相对平缓，而本文提出的算法与VoteRank、Enrenew、Degree_non以及K-shell_non方法增长趋势基本一致，增长相对快速。

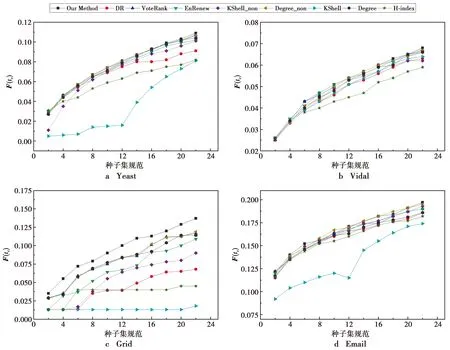
图3 不同初始化种子集大小下的结果对比Fig.3 Results under different initialized seed set sizes

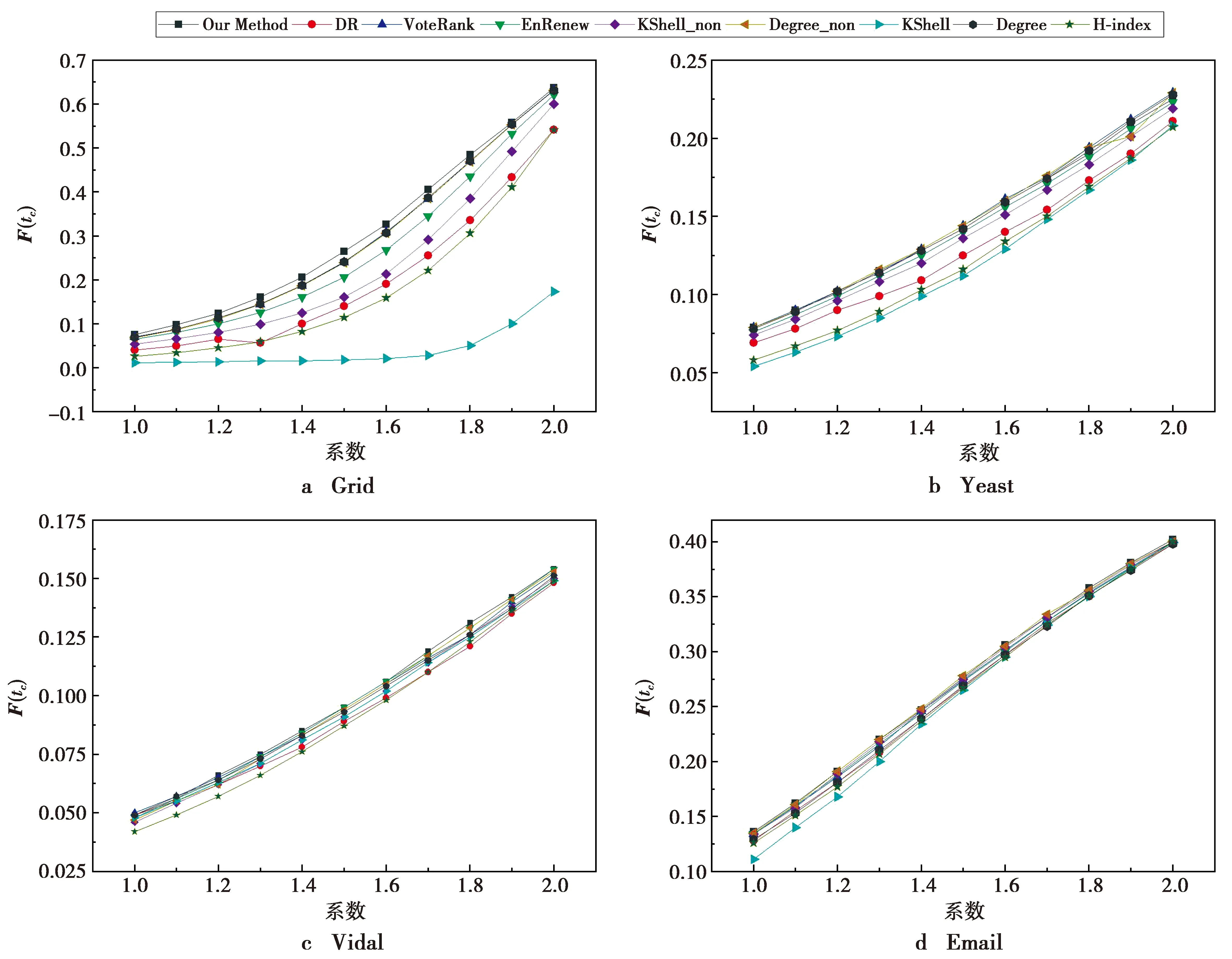
图4 不同感染概率下的结果对比Fig.4 Results under different infection probabilities

4 结 论

相较于单种子节点，具有多种子节点时，信息在网络中的传播更为复杂，在传播过程中多个节点相互影响。本文以DynamicRank为基础，提出了一种高效的基于贪心选择策略的重要节点集挖掘方法，经过多次迭代选择影响力最高的种子集。本文采用SIR模型，在4个实际网络上进行了实验和对比。实验结果表明，本文方法在大多数情况下都优于纯粹基于重要节点排序的简单选择方法，也优于重要节点集挖掘的启发式方法。不过，DynamicRank排序方法本身只考虑了3阶可达邻居，影响范围有限；而简单扩展邻域的范围一方面将极大增加计算时间的开销，另一方面也会带来一定的噪声干扰。因此，如何基于DynamicRank模型思想设计更为有效的方法挑选重要节点集，是未来的一个重要研究方向。同时，贪心算法每次迭代计算时需要遍历图中所有节点，随着图规模的增大，时间复杂度将会大大增加。因此，如何在大规模网络中利用感染率传播方法有效、快速地挖掘有影响力的传播者，是另外一个需要重点研究的问题。