基于分支定界和有效集的信号检测算法

李贵勇，李思远，于 敏

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引 言

大规模多输入多输出(multi-input multi-output，MIMO)技术，可以在保持发射功率与频谱资源的情况下，提升系统吞吐量与容量，是5G系统的关键技术之一[1-2]。其中信号检测的性能关乎大规模 MIMO系统是否可靠，信号检测复杂度关乎系统的是否易于实现，所以信号检测成为大规模 MIMO系统中至关重要的一部分。

为了提高大规模MIMO系统的性能，学者们提出了多种信号检测算法。如最大似然(maximum likelihood，ML)算法[3]、最小均方误差 (minimum mean squared error，MMSE) 算法、文献[4]提出的K-best球形检测算法和文献[5]提出的多阶段球形译码(sphere decoding，SD)检测算法。SD算法系统性能可以接近ML算法，但其复杂度会随着调制阶数和天数数量增长呈指数增加。而且从本质上来说，它属于一种分支定界(branch and bound，BB)算法[6]，它在每个分支节点上，都考虑了最小二乘问题。在BB算法的每个节点上，必须解决二次规划子问题。在非线性优化理论中有很多算法可以解决二次规划(quadratic programming，QP)问题，例如：梯度投影法和内点法。但梯度投影法复杂度高，搜索速度较慢；内点法算法中心路径设置困难，往往很难达到预期效果。文献[7]提出的主动禁忌搜索(reactive tabu search，RTS) 算法和文献[8]提出的似然上升搜索 (likelihood ascend search，LAS)算法，对进行判断得到较为良好的初始向量进行局部的相邻域搜索，平衡了天线数量增加而带来的复杂度增长和性能衰减的问题，但其系统性能还是会随着调制阶数的增长而快速恶化。文献[9]提出的似然搜索树检测(likelihood based tree search，LBTS)算法相对于BB算法进行了节点的筛选，不对所有节点进行计算，从而降低了复杂度，但当调制阶数增加时，性能会明显恶化。

为了解决传统算法不能很好地解决复杂度和系统性能上的均衡，本文就BB算法和QP算法进行了重点分析研究。首先，本文基于ML检测构建出QP命题，并且对一阶QP命题所得解向量进行二次判断，将落入阴影区域的符号判断为不可靠符号；然后，对一阶QP命题解中的不可靠符号进行具有可变二分法的深度优先分支定界算法检测，从而形成第二次QP检测；最后，为了降低BB算法复杂度，提出了一种针对上界的修剪策略，并且引入了近似因子，改善了算法性能，在复杂度和性能之间进行了更好的折中。并且，本文算法中涉及的QP命题的求解，均使用原始有效集算法[10]。

1 系统模型

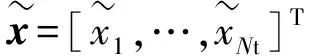
(1)

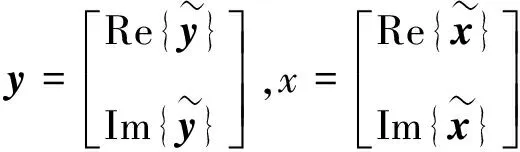
(2)

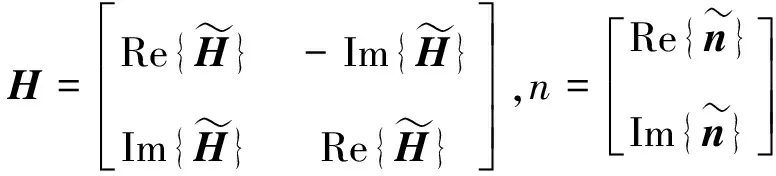
(2)式中：Re为复值向量的实部；Im为复值向量的虚部。

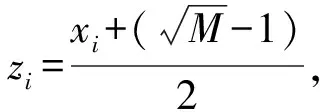
(3)

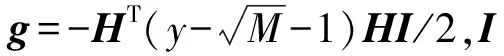
在本文中，必须解决凸二次规划的求解问题。有效集法(active set method，ASM)在求解约束条件较少的QP命题时，显示出了相当好的性能，可以用于大规模MIMO系统。原始有效集方法从一个迭代开始逐步解决子问题，在该子问题中，QP问题的不等式约束和所有等式约束被强加为等式[11]。

这里通过忽略上标考虑一般的QP子问题

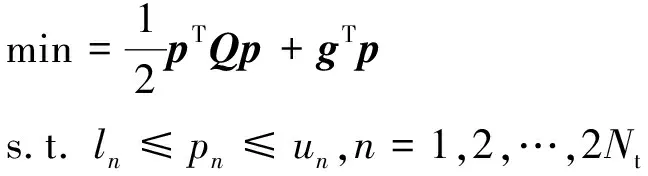
(4)

原始有效集算法步骤如下。

初始化：给出初始可行点x0，将空集W0设置为x0处的有效集

fork= 0,1,2,…,do

解式(4)，求出pk;

ifpk=0

stopx*=xk;

else

end if

else

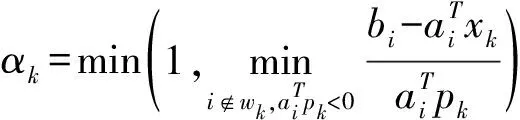
xk+1←xk+αkpk;

if 存在阻塞约束

选择阻塞约束或阻塞约束中的一个加入有效集Wk生成Wk+1。

else

Wk+1←Wk;

end if

end if

end for

2 基于QP优化问题应用分支定界和有效集法的信号检测算法

2.1 2QP算法和阴影区域介绍

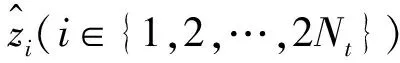
(5)

(6)

2.2 基于阴影区域的BB搜索树算法

传统BB算法是基于二叉树搜索的检测算法。例如将(6)式作为根节点问题，传统BB算法会选择每层第一个非整数元素处[14]，分支为2个互斥的子搜索空间，且作为子节点约束，这样分支后的下一层节点元素中至少有一个更接近最优解。然后逐层进行分支，缩小范围，最终就可以找到最优解。若解向量所有数值均为整数，则为最优解;否则，不是最优解。而且对有较大误差的符号进行分支可以较快地收敛，可以尽可能地减少分支次数，从而降低了算法复杂度。

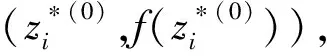
(7)

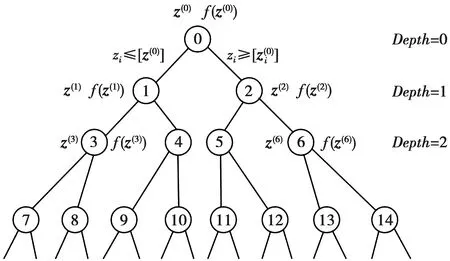
图1 分支定界搜索树Fig.1 Branch and bound search tree

如果搜索二叉树的所有节点，直至出现最优解，则复杂度非常高。假设在搜索树搜索到d层才出现最优解，则整体需要解QP的次数为2(d+1)-1。所以本文首先采用了2种针对于分支定界过程中深度和宽度的修剪的方法。

1)深度修剪。人为规定搜索的层数，即使搜索到规定的层数没有出现最优解 ，也强制不再进行后续分支，并寻找目标函数值最接近最优解的解向量。

2)宽度修剪。与传统算法在每层节点的第一个非整元素处进行分支不同，本文首先对每层各个节点对应的目标函数值进行降序排序，保留前W个节点进行分支，其余节点删除。因此，在算法分支的每个节点处都需要更新目标函数值的最大值。

其次，如果解节点优化问题所得目标函数值超过设定的目标函数最大值，则说明该节点及其之后的各分支节点不可能生成最优解，所以要在后续的节点列表中去除该节点。为了加快收敛速度，降低复杂度，本文根据此原理提出了一种分支定界过程中的针对上界的修剪原则。

根据MMSE得出的信号估计值来规定目标函数的最大值，然后使用该估计值来计算BB搜索树的起始上界。

(8)

(8)式中：f(up)表示为代价函数的起始上界；xmmse为MMSE得到的信号估计值。该起始上界将在树内被更新。因此，例如，每当f(m)>f(up)时，节点m就被修剪，f(m)为目标函数值。这种方法的优点是①整个树只需要一次计算；②在高信噪比的情况下，它可以作为紧密边界，加快搜索过程。但是在符号较多且低信噪比时，它需要更多的计算量。

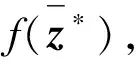
(9)

综上所述，算法步骤可以总结为算法初始化：解式(3)得到集合γ与公式(6)。

步骤1初始化节点列表为空，由(8)式得出f(up);定义深度为L和宽度为W并输入对应数值;将(6)式加载到节点列表上，开始搜索;初始化层数l=0。

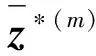
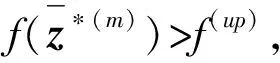
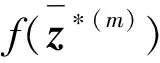
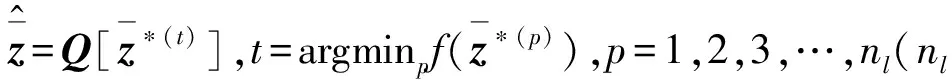
步骤6令l=l+1，跳转到步骤2。

步骤7终止算法。

2.3 复杂度分析

3 仿真分析

在仿真实验中，信道环境设置为瑞利平坦衰落信道，设置接收天线和发送天线均为32根。规定BB(16,3)表示搜索树搜索深度为16，每层保留节点数为3。为了比较本文算法的性能，我们在分析本文算法性能的同时也跟MMSE算法、QP算法、2QP算法、BB算法进行分析比较。

设置调制方式为16QAM，δ=0.25，φ=0.001。仿真结果如图2所示。根据图2可得，在低信噪比情况下传统的BB算法的性能差于QP算法和2QP算法。在信噪比为25 dB左右时，传统的BB算法的性能才优于2QP算法。但是本文算法，在低信噪比时性能也优于QP算法和2QP算法。在误比特率(bit error rate，BER)为10-4时，本文算法比2QP算法有着约3 dB的增益；比传统BB算法提升了约为2 dB。在BER=10-5时，本文算法仍保持较好的性能，与传统BB算法相比有着约为2.5 dB的增益。

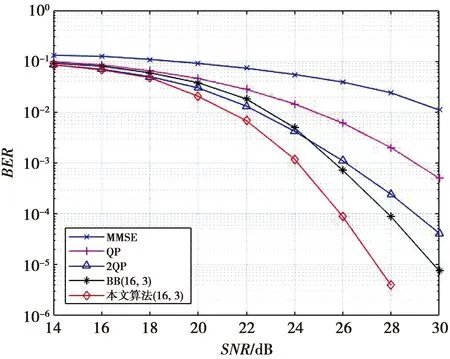
图2 32×32 16QAM BER性能比较Fig.2 Performance comparison of 32×32 16QAM BER

与图2相比，改变调制方式为64QAM，φ更改为0.000 1，其他条件保持不变，仿真结果如图3所示。当BER=10-4时，本文算法与2QP算法相比，有着约5.5 dB的增益；与传统BB算法相比，有着约1.8 dB的增益。

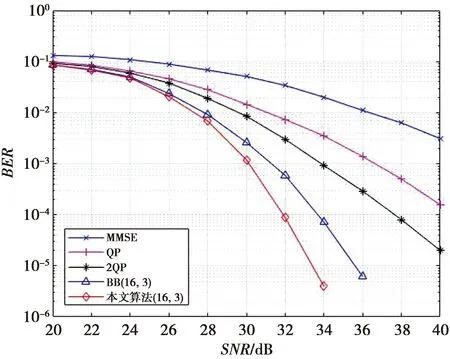
图3 32×32 64QAM BER性能比较Fig.3 Performance comparison of 32×32 64QAM BER

最后提高调制阶数，使用256QAM调制来验证本文算法在高阶调制的性能，其他条件保持不变，仿真结果如4所示。当BER=10-4时，本文算法比2QP算法有着约为6 dB的增益；当BER=10-5时，本文算法比BB算法有着约为3 dB的增益。从图2—图4中的性能比较上可以看出，本文算法在不同的QAM调制阶数上，性能稳定，均优于传统的QP算法、2QP算法和BB搜索树算法。

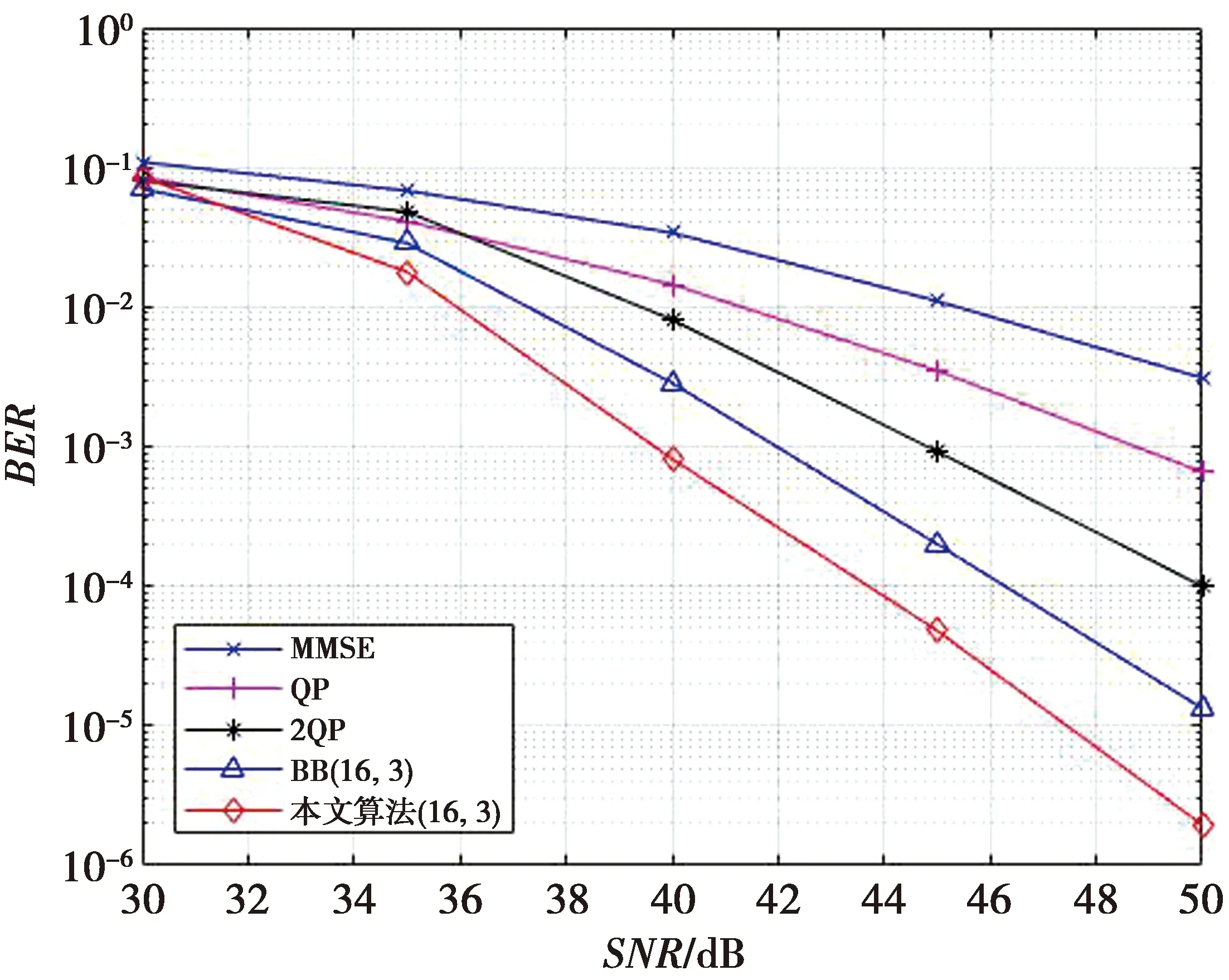
图4 32×32 256QAM BER性能比较Fig.4 Performance comparison of 32×32 256QAM BER

如果在本文算法中放宽修剪条件fm≥fup，在一阶QP算法后的分支定界算法中会减少求解的节点数，从而导致精确度减少性能下降，但同时求解节点数的减少也会带来复杂度的降低，这就给我们在性能和复杂度之间的折中提供了的新思路。在这本文引入一个近似因子e(e∈[0,1])。将修剪条件替换为fm≥(1-e)fup。显然，当e=0时，与精确的本文算法相同。当e=1时，与根节点的初始解相同。图5为调制方式为16QAM，δ=0.25，φ=0.001时的天线数目32×32 MIMO信道的性能。当BER=10-4时，精确的本文算法比近似因子e为0.3、0.6的本文算法分别有着约为0.5 dB、1.2 dB的增益。虽然引入了修剪因子后的算法性能降低了，但是从图5中还是可以看出，性能相较于传统BB、2QP算法依旧有着提升。

4 结 论

本文基于QP检测器提出了一种适用于高阶调制的大规模MIMO系统的低复杂度检测算法。本文算法应用了有效集法和具有可变二分法的深度优先分支定界算法，结合阴影区域，将不可靠符合进行搜索树检测；提出了一种修剪策略，同时引入了近似因子，改善了传统QP检测器的性能。结果表明，本文算法与BB算法相比复杂度较低，特别是在高信噪比和高QAM调制的情况下，并且本文算法在性能上均优于传统QP算法、2QP算法和BB搜索树算法。

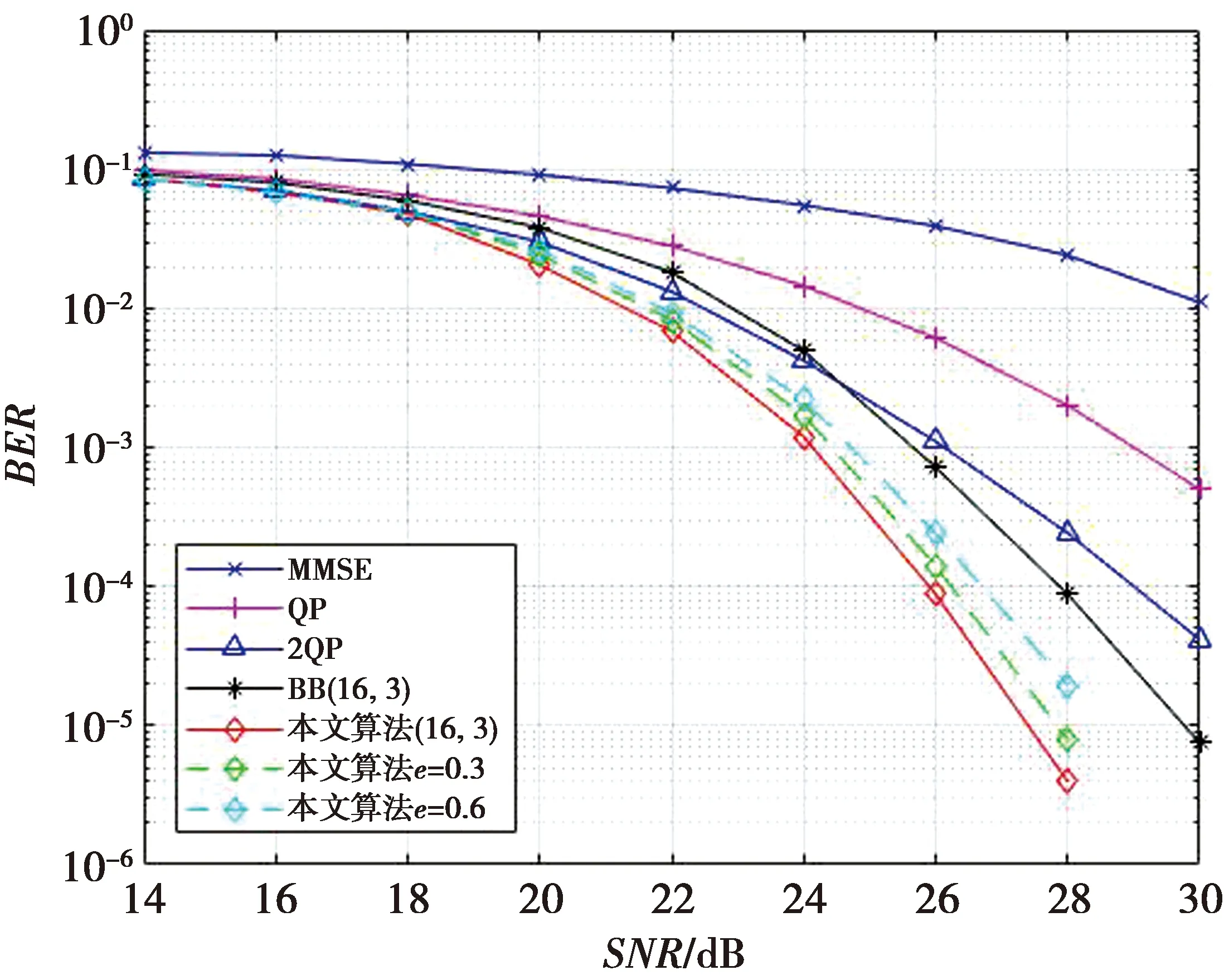
图5 引入近似因子e后与其他算法性能的比较Fig.5 Performance comparison with other algorithms after introducing approximation factor e