基于超短基线的GPS测姿算法研究

宋雅倩，何 维，任 彦

(重庆邮电大学 通信与信息工程学院，重庆 400065)

0 引 言

姿态角是载体在惯性空间指向过程中的重要导航参数之一。这些参数可以帮助了解载体在空中的实时姿态，在军事、民用等方面都有着重要的作用。

常用的测姿主要分为卫星测姿、惯性导航系统(inertial navigation system, INS)测姿两大类。惯性测量单元是通过加速度计和陀螺仪测量载体的姿态，陀螺仪的误差会随着时间的推移而增大，且高精度的INS系统成本较高[1]。同INS测姿相比，全球定位系统(global positioning system, GPS)测姿系统只需要利用低成本的接收机就可以提供较高精度的姿态信息，同时还可以完成载体定位和系统授时，能够长时间进行高精度测姿任务[2]。

正常情况下，卫星测姿的精度将随着基线长度的增加而升高，而例如在无人机、基站天线、无人驾驶车等超短基线情况下长基线产品无法应用。超短基线由于两端之间非常接近，使得两端的测量误差有很强的相关性，并且很小的整周周跳都将对基线的解算精度产生重大影响，因此，整周模糊度确定是超短基线测姿的核心之一；同时，基于基线求解的姿态解算方法将直接影响着姿态结果，因此，测姿算法的研究十分必要[3]。文献[4]提出了一种基于低成本接收机的双天线测姿算法，当基线长度为1.1 m时，测姿航向角精度在1°左右，但其需要双系统并且基线长度较长；文献[5]提出了一种GPS/INS组合导航算法，但陀螺仪测量精度随着时间的推移会逐渐降低，只有在短时间内精度高；文献[6]通过建立了双差分相位观测值与姿态四元数之间的函数关系使姿态解算更精准，在静态超短基线为0.55 m浮点模糊度的准确性得到了提高，姿态解算更精准，但是其需要用到多天线。

整周模糊度确定是超短基线测姿的核心之一，目前现存的整周模糊度的方法，都需要求解模糊度实数解，构建模糊度搜索空间，并利用一定的假设检验条件在构建的搜索空间内搜索出正确的整周模糊度。浮点模糊度一般由伪距观测值、最小二乘法或卡尔曼滤波平滑获得。并且浮点模糊度的准确性会影响整数模糊度分辨率的性能[7]。整周模糊度的固定方法有模糊度函数法、最小二乘模糊度搜索法、快速模糊度算法 (fast ambiguty resolution approach,FARA)法、快速模糊度搜索滤波法、模糊度最小二乘去相关平差法(modified least-squares ambiguity decorrelation adjustment algorithm, M-LAMBDA)[8]。目前有学者提出改进模糊度最小二乘去相关平差法(modified least-squares ambiguity decorrelation adjustment algorithm, M-LAMBDA)算法，通过提前置换和动态调整搜索范围能够有效提高传统LAMBDA的计算效率，且不会对模糊度固定成功率造成影响[9]。

姿态角的解算将在基线求解的基础上进行，受基线精度影响较大，目前基于卫星测姿的姿态角算法大致分为直接法、最优估计方法、最小二乘法和滤波算法[10]。直接法是直接通过观测值求解，容易实现，硬件要求低，但不能同时利用已知基线长度的先验信息；最优估计算法需要大量的观测值来进行迭代求解最优值；最小二乘法是采用最小二乘理论来求解姿态矩阵，其默认为线性估计，其结果并不是最优值；滤波法是指采用例如卡尔曼滤波、粒子滤波等方法求解姿态角，但滤波法对初值的选取较为敏感，较为精准的初值适用于卡尔曼滤波，不太精准的初始条件适用于粒子滤波[11]。

通过以上分析，区别于其他GPS测姿算法，本文提出的改进GPS测姿算法适用于更短的基线，在求解浮点模糊度时采用改进扩展卡尔曼滤波，有效提高测姿系统的可靠性，在姿态解算时采用滤波法，有效提高了测姿系统的稳定性。

1 GPS测姿算法模型推导

1.1 系统组成及功能

本文提出的基于超短基线的GPS测姿系统框图如图1所示。

图1 GPS测姿系统框架Fig.1 Framework of GPS attitude measurement system

1)转台：利用转台来控制基线航向角的变化。

2)接收机：user、reference接收机为2台GPS天线，用来接收卫星数据。

3)OEM617D板卡：将2个天线连接板卡，串口1输入命令获得观测数据与星历数据。串口2输入命令获得观测数据。

4)笔记本：处理数据，进行算法验证与分析。

算法验证主要分为5部分：数据解析、周跳检测与修复模块、扩展卡尔曼滤波模块、MLAMBDA算法模块和姿态解算模块，本文重点研究扩展卡尔曼滤波模块和姿态解算模块。

1.2 基于扩展卡尔曼滤波的模型推导

在进行滤波前，利用载波相位测量值进行周跳检测[12]。在双频情况下，reference站的坐标通过单点定位得知，user站的坐标初始模糊位置通过单点定位可知，则X可以表示为

(1)

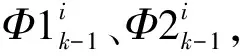
(2)

设在k-1时刻，频点为f1，公共卫星为1到6。假设卫星1有周跳，这时候需要将卫星1的单差模糊度赋值为0，则

(3)

设在k时刻，单差模糊度浮点解为

(4)

将k-1时刻不为零的单差模糊度与k时刻对应的单差模糊度做差，将每个差值相加求平均av，有

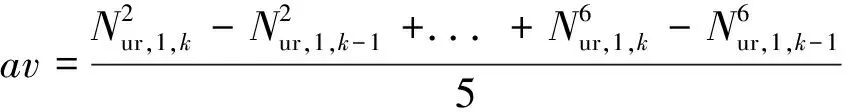
(5)

(5)式中，n为公共卫星的个数，即Nur,1,k为

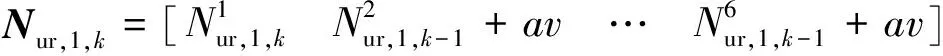
(6)

扩展卡尔曼滤波(extended Kalman filtering,EKF)针对于非线性系统，通过系统输入输出观测数据，使得系统的估计值有最小均方误差。利用泰勒公式对高阶项采用忽略或逼近措施，从而使非线性系统转变为一个线性系统，再利用卡尔曼滤波方法进行最优估计。扩展卡尔曼滤波观测方程与状态方程分别为

zk=h(xk)+vk

xk=Fxk-1+u

(7)

(7)式中：zk为观测向量；xk为当前状态向量；xk-1是上一时刻的状态后验估计值矩阵。F是的传递矩阵，vk为系统残差，由载波相位残差和伪距残差2部分构成，即

(8)

预测方程为

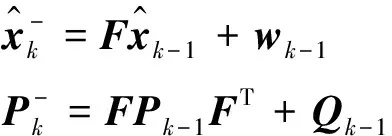
(9)

(10)

设本模型的状态变量为经过整周跳变与修正的Xk，则状态方程为

(11)

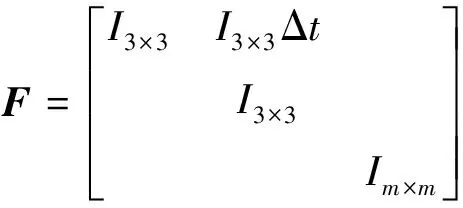
(12)

当Δt为零时，为静态状态，Δt不为零时为动态模型，因此，预方程为[4]

(13)

(13)式中：Q为上一时刻k-1到此刻k外界提供给滤波器的过程噪声方差，根据经验值将状态向量的协方差矩阵初始化为[4，13]

(14)

(15)

(15)式中：

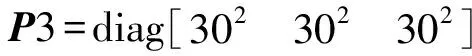
P0的值会随着扩展卡尔曼滤波的每一次的迭代而变化。

已知双差载波观测方程和双差伪距观测方程为

(16)

模型中选取最高仰角卫星作为参考卫星，将参考卫星与其他卫星的双差观测方程的左侧作为观测值z，即选取(16)式左侧部分(GPS接收机板卡输出)作为观测值，若假设最高仰角卫星编号为1，则

(17)

(17)式中，当高仰角卫星编号不为1时，Φi与Pi的值会变化。选取(16)式右边一部分为h(X′)，即

(18)

将h(X′)非线性函数转化为近似的线性函数

(19)

(19)式中，偏导项被称为雅可比式H。测量更新的3个方程为

(20)

(20)式中，R为测量噪声矩阵，表示测量值与真实值之间的差值。

1.3 GPS观测量误差随机模型

若要符合标准Kalman滤波的条件，那么就要保证有正确的系统模型、量测模型和量测噪声。同时正确给定函数模型和随机模型对于GPS定位结果的估计和观测量的粗差探测均至关重要。在GPS应用中，R为测量噪声矩阵，本文采用不同的模型，应用于扩展卡尔曼滤波模型中，对GPS基线解算的不同结果进行分析比较。测量噪声矩阵R表示为

(21)

当采用卫星高度角的GPS观测量随机模型时

(22)

(22)式中：i对应参考卫星；a,b为载波相位观测误差；c为基线向量观测误差；d为卫星时钟稳定误差。其中，a,b经验固定值0.003，c,d为0，e对应卫星的高度角。该随机模型的实质是利用低高度角卫星受到大气延迟较大，且容易产生多路径效应的特点，将卫星高度角较低的观测值赋较低的权。

1.4 整周模糊度求解

LAMBDA算法最早是由Teunissen[14]提出，该算法主要是利用Z变化将模糊度的搜索空间去相关化，使得模糊度搜索空间减小。但传统的LAMBDA计算效率低，通过后者不断修正，提出了M-LAMBDA算法，M-LAMBDA通过改进搜索空间，使得计算效率提高。

由前面的扩展卡尔曼滤波得到了双差模型下的流动站坐标和单差模糊度浮点解，在M-LAMBDA求整数解的过程中，将单差通过转换矩阵转化为双差，提高整周模糊度的求解精度，并提升求解效率。

(23)

已知单差模型下的方差-协方差矩阵为Pk，则双差模型下的方差-协方差矩阵为

(24)

(25)

1.5 姿态解算

在卫星与接收机位置解算过程中，由GPS接收机测得参考站在地心地固坐标系下的坐(xr,yr,zr)，首先将其转为大地坐标系(φ,λ,h)，转换公式为

(26)

(26)式中：N为基准椭球体的卯酉圆曲率半径；e为椭球偏心率；a基准椭球体的长半径；b为短半径。基线向量l为

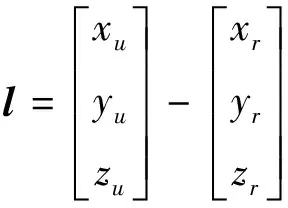
(27)

将基线的地心坐标系转化为站心坐标系为

(28)

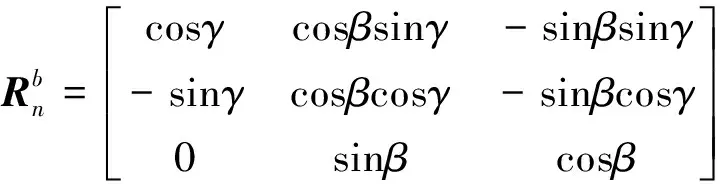
(29)

基线在载体坐标系下可表示为[0|bl|0]T可以测量载体的航向角γ和俯仰角β，则

(30)

若采用直接法，则俯仰角和航向角的结果为

(31)

若采用滤波法，滤波采用扩展卡尔曼滤波，对(30)式简化为

yenu=|l|f(β,γ)

(32)

对(32)式进行线性化，其中俯仰角和横滚角的初始值β0、γ0采用直接法测姿获得。雅可比阵为

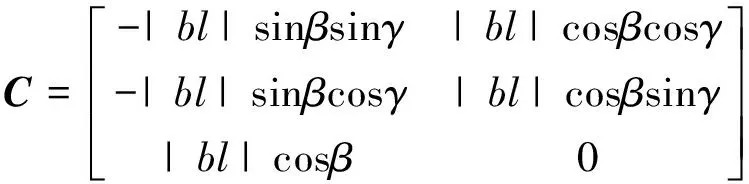
(33)

yenu=Cxθ+vθ,k

(34)

预测方程为

(35)

校正方程为

(36)

(37)

(37)式中，wk为均值0方差0.1的正态白噪声，vk为均值0方差2的正态白噪声。

2 算法验证与结果分析

2.1 测试环境

本文选取在重庆邮电大学逸夫楼楼顶进行测试。测试平台如图2所示，选择OEM617D板卡进行接收数据，得到卫星数据与观测数据，采用精准转台固定航向角度，2个天线同时工作，天线之间的距离为基线长度，然后通过Python软件进行算法验证。

图2 测试环境Fig.2 Testing environment

2.2 系统验证以及结果分析

图3、图4为分别用最小二乘法和扩展卡尔曼滤波在20、40、100 cm的120°航向角情况下求解浮点模糊度的航向角的误差。由图3，图4可知，在基线长度为100 cm情况下，最小二乘法和扩展卡尔曼滤波产生的航向角误差相差不大，但随着基线长度的减小最小二乘法的航向角误差逐渐增大，在20 cm时已经完全不准确，因为随着基线的减小观测误差逐渐增大，最小二乘法只能利用当前的观测量，不能对观测量进行误差分析，因此，定位结果受观测量的误差影响比较大，精度不高。扩展卡尔曼滤波的误差相对稳定，因为扩展卡尔曼滤波在时间上具有相关性，利用观测残差，不断修正预测值并利用测量噪声协方差矩阵和过程噪声协方差矩阵控制最终的结果中测量值所占的权重。证明了在超短基线情况下，扩展卡尔曼滤波求解模糊度浮点解比最小二乘模糊度浮点解更适用。从图4也看出，随着基线的减小，航向角的可靠性和稳定性减小，因此，本文提出对扩展卡尔曼滤波进行改进提高航向角的可靠性，采取滤波法提高航向角的稳定性。

图3 最小二乘求解浮点模糊度导致航向角的误差Fig.3 Least square method for solving the heading angle error caused by floating point ambiguity

图4 EKF求解浮点模糊度导致航向角误差Fig.4 Heading angle error caused by floating point ambiguity solved by EKF

在静态情况下基线长度为20 cm，每30°为一方位角对等权模型和基于卫星高度角模型产生的航向角均方误差进行对比，如图5所示。从图5可以看出，在不同航向角的情况下基于卫星高度角模型明显比等权模型的均方误差小。证明静态下基于卫星高度角的随机模型使超短基线的姿态解算可靠性提高。其原理为若假设所有观测量误差相同的方差，但实际中存在大量的冗余观测量，会导致粗差无法检测，降低参数估计精度。基于卫星高度角的随机模型可以有效削弱大气残差，部分减少多路径效应影响，而且该随机模型易于实现，且能较好地反映观测量误差，提高参数估计精度。

图5 静态时不同模型情况下航向角的均方误差Fig.5 Mean square error of heading angle under different model conditions at static state

在静态情况下基线长度为20 cm，每30°为一方位角利用直接法和滤波法的航向角误差方差进行对比，如图6所示。从图6可以看出，在不同航向角的情况下滤波法比直接法稳定性大大提高。图6证明了滤波法提高了静态测姿系统的稳定性。其原理为直接法解算姿态计算过程简单，解算速度快，但不能利用基线已知的信息来估计姿态角，因此，其估计值是次优的，滤波法利用直接法提供初始值，利用时间上的相关性不断进行迭代更新，提高参数估计的精度。

图6 静态时不同测姿算法下的航向角误差方差Fig.6 Heading Angle error variance of different attitude measurement algorithms at static state

在动态情况下，基线长度分别为100、40、20 cm，航向角每秒6°进行变化，分别在等权模型和基于卫星高度角模型下进行误差的均方误差比较，如图7所示。从图7可以看出，随着基线的减小均方误差不断增大，但基于卫星高度角模型的均方误差明显比等权模型下的均方误差小。证明了基于卫星高度角模型提高了超短基线下动态测姿系统的可靠性。

图7 动态时不同模型情况下航向角的均方误差Fig.7 Mean square error of heading angle under different model conditions in dynamic condition

在动态情况下，基线长度分别为100、40、20 cm，航向角每秒6°进行变化，分别在直接法和滤波法下进行误差的均方误差比较，如图8所示。从图8可以看出，随着基线长度的减小误差方差不断增大，但基于滤波法的误差方差小于直接法的误差方差。证明了滤波法提高了超短基线下动态测姿系统的稳定性。

图8 动态时不同测姿算法下的航向角误差方差Fig.8 Heading angle error variance of different attitude measurement algorithms in dynamic condition

图9为静态下基线长度为20 cm时，利用本文算法与其他算法对200个历元内航向角为150°采集的数据进行解算的结果对比图；图10为动态时基线长度为20 cm，利用本文算法与其他算法分别对60个历元内航向角以每秒6°变化的数据进行解算的结果对比图。从图9—图10可以看出，无论是在静态状态下还是动态状态下，本文提出的算法更加适用于超短基线测姿。

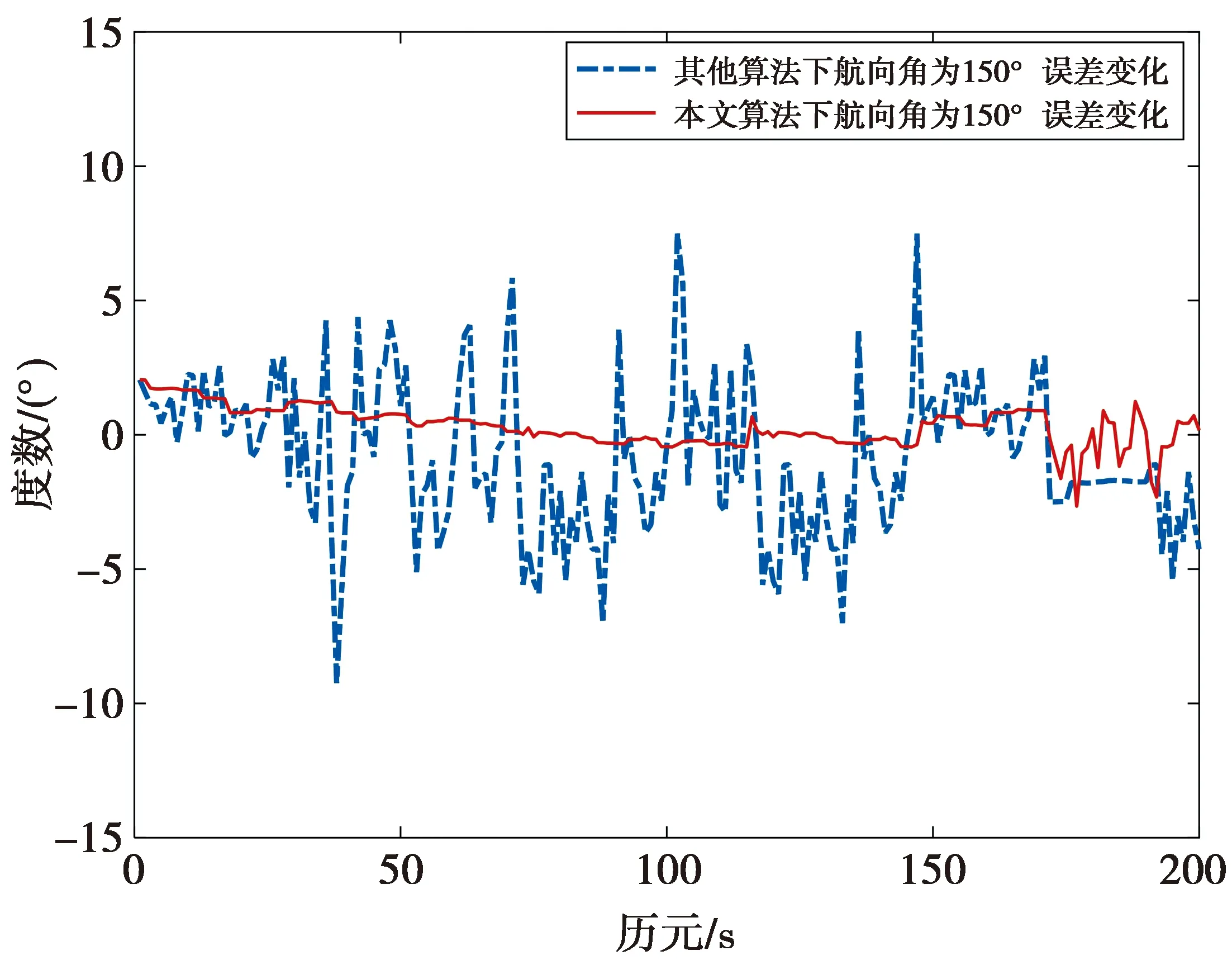
图9 基线为20 cm静态时航向角误差变化对比图Fig.9 Comparison chart of heading angle error when the baseline is 20 cm static state

图10 基线为20 cm动态时航向角误差对比图Fig.10 Comparison chart of heading angle error when the baseline is 20 cm dynamic state

3 结 论

本文提出一种提高超短基线姿态测量稳定度与可靠性的GPS测姿系统，利用改进扩展卡尔曼滤波来为MLAMBDA提供精准的模糊度浮点解，提高测姿系统可靠性。采用滤波法进行姿态解算，有效地提高了测姿系统的稳定性。结果表明，该系统在基线长度为20 cm的静态情况下，误差方差为0.1左右，并且其航向角的精度为2°左右。该系统在基线长度为20 cm的动态情况下，误差方差为2左右，并且其航向角的精度为3°左右。与其他测姿系统相比，该系统在测姿可靠性和稳定性上都有所提高，且结构简单，易于集成，成本低，可应用于大部分的超短基线测姿场景。