基于KF-SRUKF算法的锂离子电池荷电状态估计

任碧莹，孙 佳，孙向东，谢晨雪

(西安理工大学电气工程学院，陕西 西安 710054)

1 引言

锂离子电池因具有安全性高、能量密度高、自放电效率低、循环使用寿命长等优点被广泛应用于各个领域[1]。但是，锂离子电池的过充、过放现象会对电池造成不可逆转的损坏，影响电池的性能和寿命[2]。为了保证锂电池的安全性，电池管理系统迫切需要一种可靠、准确、易实现的荷电状态(State Of Charge, SOC)估计方法[3]。

目前，SOC估计方法分为两种：间接法和直接法。在间接法中，电池SOC通过其他物理量来评估。电池开路电压作为一种间接方法，需将锂电池与负载分开，并在静置到稳定状态后进行测量，因此该方法不适用于在线检测系统[4]。电化学阻抗谱法作为另一种常见的间接方法[5]，该方法不仅可用于估计SOC，还可用于估计健康状况，但是阻抗谱的测量对所用仪器要求较高，在实际应用中难以实现。

安时积分法是SOC直接估计的方法之一，其将电池电流进行积分来估计SOC，但需要已知初始SOC，并且估计精度受到测量误差和累积误差的影响。智能算法的引入使得SOC估计精度有所提升，例如神经网络法[6]、滑模观测器法[7]、粒子滤波器法等[8]，虽然这些方法可以较准确地估计电池SOC，但由于需要大量的样本并且计算复杂，很难在线使用。

扩展卡尔曼滤波器(Extended Kalman Filter, EKF)因设计简单被广泛应用于电池的SOC估计[9-11]。基于锂电池的非线性状态空间模型，EKF使用泰勒级数的一阶项进行非线性函数线性化，得到近似的线性化模型，该过程将模型的二阶及以上的项忽略掉，产生了一定的误差，再进行状态变量的估计，则会降低SOC估计的精度。无迹卡尔曼滤波器(Unscented Kalman Filter, UKF)通过使用无迹变换(Unscented Transformation，UT)计算平均值和协方差算法来逼近系统的非线性模型，进一步提高SOC估计的精度。但是由于计算机字长限制，使计算中舍入误差和截断误差累积，造成协方差矩阵失去正定性，导致UKF失去稳定性。针对此问题，文献[12-16]将平方根无迹卡尔曼滤波器(Square Root Unscented Kalman Filter, SRUKF)应用于电池SOC估计，文献[12-15]均进行了一次Sigma点采样以及权值计算，针对状态方程和输出方程，先后进行两次采样点非线性传递以及均值和协方差平方根矩阵的求取，进行SOC估计；文献[16]为了考虑噪声方差的影响、提高估计精度，进行了两次Sigma点采样以及权值计算、两次采样点非线性传递以及均值和协方差平方根矩阵的求取。文献[12-16]虽然利用SRUKF算法解决了UKF算法不稳定的问题，但不论是UKF算法还是SRUKF算法，都是为了实现非线性方程变量的有效估计，而在SOC估计方程中其状态方程为线性，仅输出方程为非线性，所以SRUKF并不适合用于其状态变量的估计。因此文献[12-16]中的SOC估计过程无疑增加了不必要的计算量，并且UT变换的近似求解降低了估算精度。

针对上述问题，本文将在SRUKF进行SOC估计的基础上，提出了将卡尔曼滤波器(Kalman Filter,KF)与SRUKF组成的KF-SRUKF算法应用于电池SOC估计中，其中KF用于线性状态方程的计算，SRUKF则用于非线性输出方程的计算。该算法解决了SRUKF用于SOC估计中对线性状态方程的不适用问题，同时也保证了算法的稳定性，提高了SOC的估计性能。

2 锂电池建模及参数辨识

2.1 锂电池二阶RC模型

本文选用二阶RC模型作为锂电池等效电路模型，因其较Rint模型、PNGV模型、高阶RC模型等具有精确度高且算法量适中的优势，其电路图如图1所示。图1中，UL为锂电池端电压；Uoc为开路电压，其为SOC的函数；R0为欧姆电阻；R1、R2和C1、C2分别为极化电阻和极化电容；I为电池工作电流，充电为负，放电为正。

图1 锂电池二阶RC等效电路模型

根据基尔霍夫定律，以两个并联RC网络的端电压U1和U2以及锂电池的SOC作为状态变量，以端电流I作为系统输入量，端电压UL作为系统输出量，在考虑噪声的情况下，可建立如式(1)所示的状态空间模型。

(1)

式(1)中的状态方程明显为线性，输出方程中由于Uoc和状态变量SOC的高次非线性关系而导致系统输出Z和状态向量x为非线性关系，从而输出方程表现为非线性。现将式(1)简写为如下形式：

(2)

式中，函数f[x(k),I(k)]表示线性关系；函数h[x(k),I(k)]表示非线性关系。

2.2 锂电池参数辨识

等效电路模型需要辨识的参数包括R0、R1、R2、C1、C2，基于二阶RC等效电路模型参数辨识的差分方程如式(3)所示，其中Y=Uoc-UL。θ1～θ5为需要辨识的参数。

(3)

定义：

则式(3)可写为如下形式：

(4)

式(4)为用于参数辨识的表达式。θ1～θ5通过相关参数辨识得到后，令θ0=T2/(θ1+θ2-1)，a=θ0θ2，b=-θ0(θ1+2θ2)/T，c=θ0(θ3+θ4+θ5)/T2，d=-θ0(θ4+2θ5)/T。根据计算的a、b、c、d结合式(5)可推得等效电路模型的各个参数。

(5)

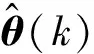
(6)

(7)

(8)

图2 BLRLS算法参数辨识流程图

3 锂离子电池SOC估计

3.1 SRUKF算法用于SOC估计存在的问题

UKF是一种利用多点采样的策略实现非线性函数有效逼近的方法，其核心思想是UT，UT在进行Sigma点集的获取时有协方差矩阵的求根运算，但由于计算机的迭代计算存在误差且有字长的限制，会使根号下的矩阵出现非正定的情况，从而影响UKF算法的稳定运行。

SRUKF则是在UKF的基础上，利用QR分解和Cholesky分解得到误差协方差矩阵的平方根，从而直接采用协方差的平方根代替UKF中的协方差进行递推运算，解决了UKF算法不稳定的问题，提高了算法的可靠性。SRUKF大致的计算流程如图3所示。

从图3可以看出，SRUKF在计算过程中运用了两次UT，分别在状态变量和输出变量的估计过程中。UT是为了实现非线性方程变量的有效估计，而根据式(1)，用于SOC估计的状态方程表现为线性，UT的近似求解无疑会增大不必要的计算量，并且降低了估算精度。所以SRUKF虽然能够保证算法的稳定运行，但它也存在和UKF一样的问题，即只适用于非线性方程变量的有效估计。

3.2 KF-SRUKF估计策略

针对上述3.1节SRUKF算法所存在的问题，本文将适合线性系统的卡尔曼滤波器与适合非线性系统的SRUKF相结合，提出了KF-SRUKF算法。针对线性状态方程，采用KF算法对状态变量进行估计，不仅避免了SRUKF算法所产生的不必要的复杂计算，提高了整体的运算效率；而且解决了 SRUKF对于线性状态方程的不适用性问题，提高了状态估计的精度；针对非线性输出方程，则采用SRUKF算法实现对输出变量的估计。整体算法利用QR分解和Cholesky分解得到协方差矩阵P的平方根S来进行传递，提高了算法的稳定性。

将所提算法KF-SRUKF应用于电池SOC估计系统的基本步骤如下：

(9)

步骤二：协方差平方根的一步预测。利用QR分解进而得到KF算法中协方差矩阵Pu(k+1|k)=A(k)Pu(k|k)A(k)T+Q的平方根，如式(10)所示。

(10)

步骤三：Sigma点集以及权重的获取。

(11)

(12)

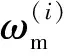
步骤四：将步骤三得到的多个Sigma点分别代入输出方程，得出多个观测量。

Z(i)(k+1|k)=h[x(i)(k+1|k),I(k)]

(13)

步骤五：获取观测量均值。

(14)

步骤六：通过QR分解以及Cholesky因子的更新最终得到协方差的平方根S的更新值。

(15)

(16)

式中，SZkZk为观测量自协方差矩阵平方根。

步骤七：求解协方差矩阵。

(17)

式中，PxkZk为状态量和观测量的协方差矩阵。

步骤八：计算Kalman增益矩阵。

(18)

步骤九：状态向量、协方差矩阵的更新。

(19)

(20)

根据以上所述步骤，可将KF-SRUKF算法的计算流程简化为如图4所示。

图4 KF-SRUKF用于SOC估计的流程图

在采用KF-SRUKF进行电池SOC估计时，针对状态方程，采用简单精确的KF，在减小计算量的同时实现高精度估计；对于输出方程，将预测后的结果应用UT变换，产生对应的Sigma点集，再对此点集进行输出方程非线函数的传递，以获得高精度的状态变量估计，这种将UT变换后移的处理方式，充分考虑到了系统噪声对状态变量估计的影响，有利于改善SOC的估计性能。

4 实验结果分析

为了验证KF-SRUKF算法用于SOC估计的性能，进行实验的测试与分析，测试平台如图5所示，由被测锂离子电池、专用电池测量设备、通信线和带有专用测试软件的计算机组成，其中被测锂离子电池的主要参数见表1。

4.1 锂电池开路电压与SOC关系曲线

锂电池开路电压与SOC之间存在着非线性关系。为了得到开路电压与SOC的关系，忽略电压“迟滞现象”，通过电池测量设备对电池进行间歇恒流放电实验。实验过程为：在室温环境(26 ℃左右)下，采用(1/3)C电流从SOC为100%开始放电，每次放电18 min，静置40 min，使得锂电池在进行下一次循环之前达到稳定状态，进而将测量的端电压作为此时的开路电压，重复此过程，直至电池达到放电截止电压2.5 V。图6为间歇恒流放电的过程。

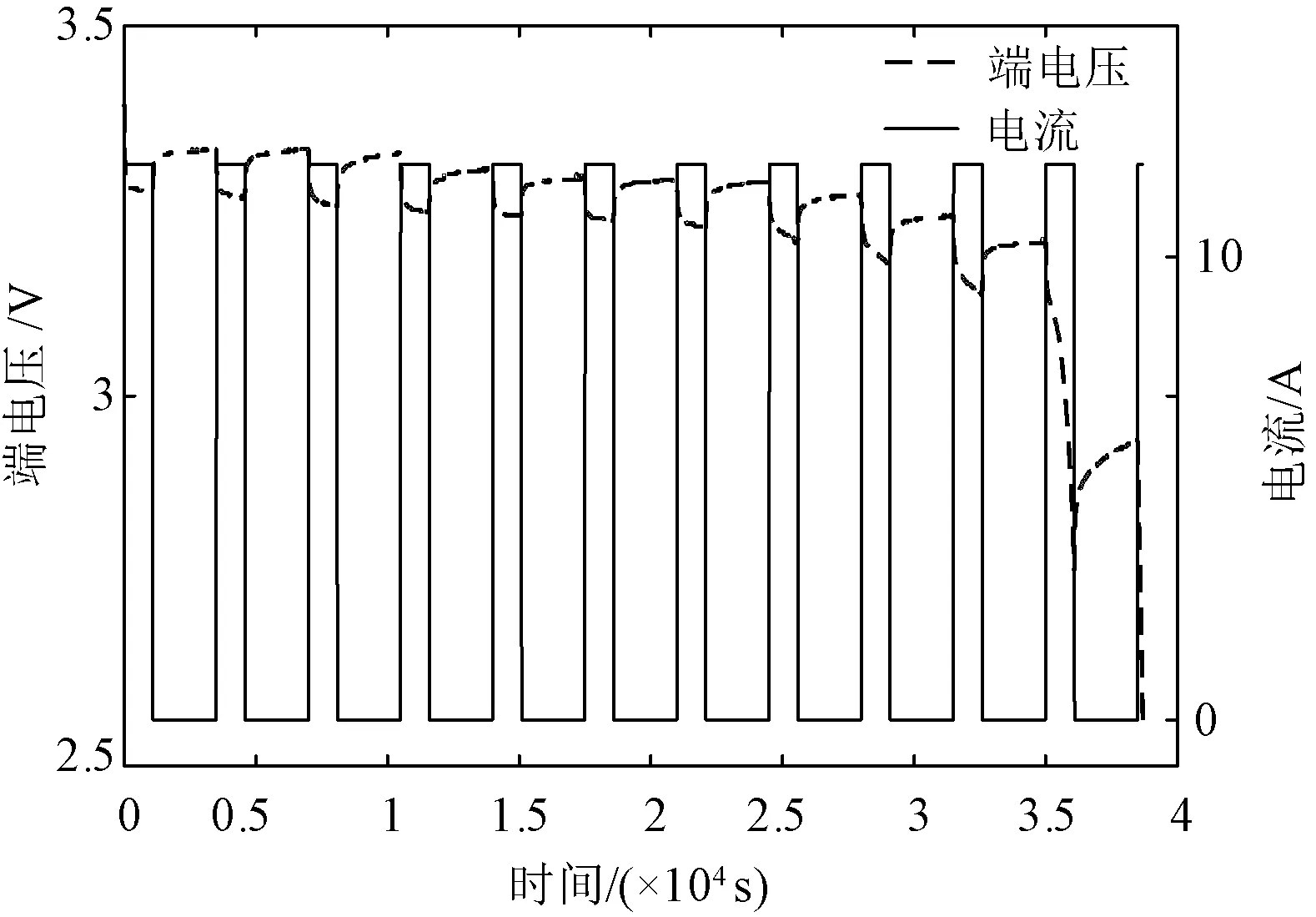
图6 间歇恒流放电过程

经上述实验可以获得12个Uoc与SOC对应的离散点，其中SOC是经电池测量仪器通过已放出容量与总容量比值获得的。为了确定整个过程中SOC与Uoc的关系，需要将此离散点进行曲线拟合，常用的拟合方法有：五次多项式拟合[12,19]、七次多项式拟合[10,15]和根据式(21)的拟合方法[20-22]，拟合结果如图7所示。从图7中可以看出，采用多项式拟合时，开路电压会随着SOC的变化上下波动，此与锂离子电池开路电压平坦的特性不符，因此选用式(21)进行曲线拟合，得到参数值分别为：ɑ1=3.312，ɑ2=0.019 32，ɑ3=-0.003 7，ɑ4=0.029 65，ɑ5=-0.007 08。

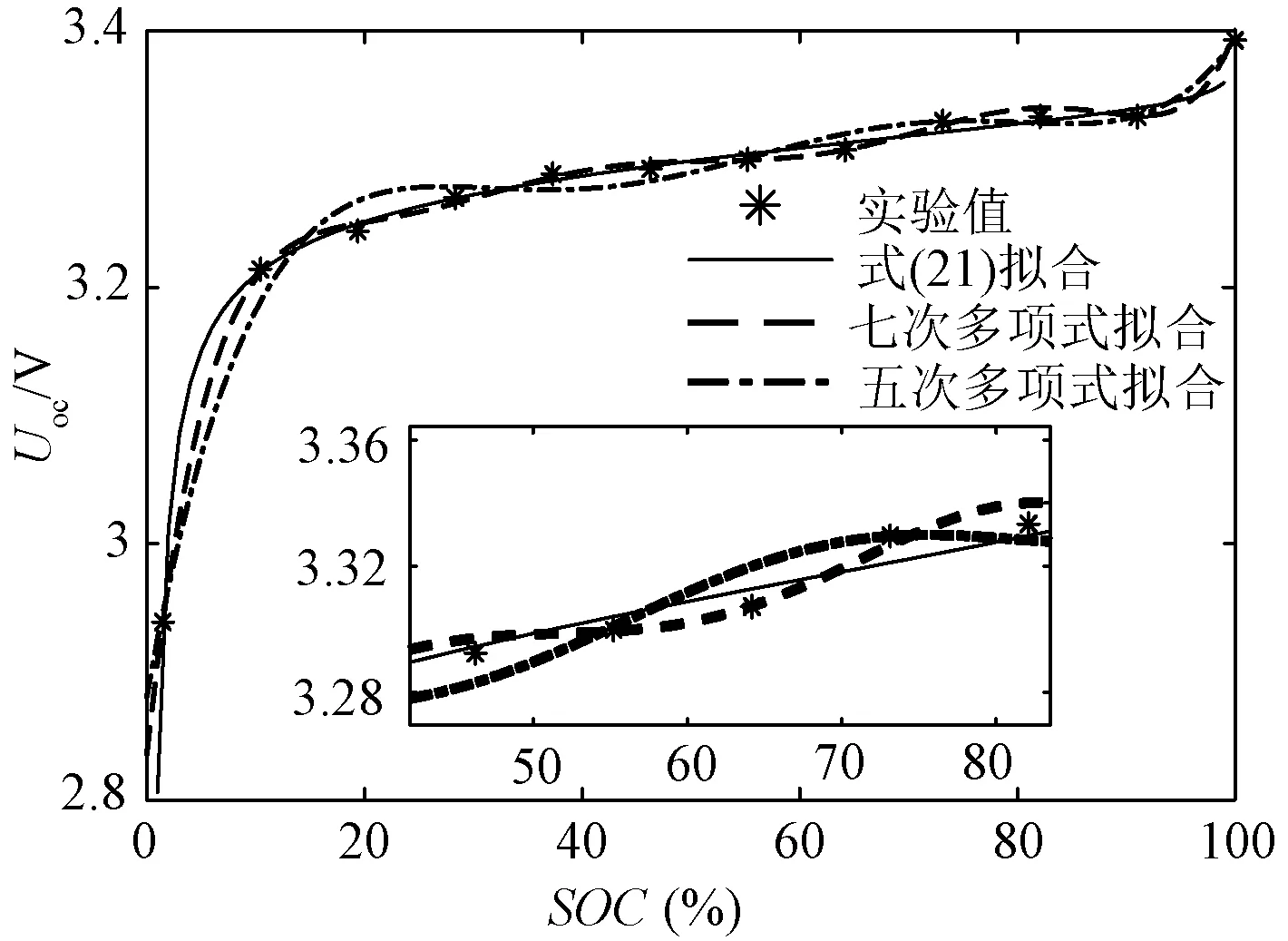
图7 SOC-Uoc充放电关系曲线

(21)

4.2 参数辨识结果验证

为了验证电池模型与参数辨识的性能，本文通过如图6所示的间歇恒流放电实验进行验证。图8为间歇恒流放电下，采用VFFRLS和BLRLS的参数辨识结果计算得到的端电压与真实端电压对比及误差对比。

图8 端电压辨识结果及误差对比

从图8(a)中可以看出，两种参数辨识方法获得的端电压曲线与真实端电压曲线均基本保持一致，而从图8(b)中可以直观看出BLRLS算法的参数辨识精度要高于VFFRLS算法。为了更好地比较两种算法的参数辨识性能，本文将对各个算法辨识的端电压从均方根误差(Root Mean Square Error,RMSE)和平均相对误差(Mean Relative Error,MRE)两方面进行分析，其计算公式如式(22)所示，实测值为端电压实测值，估计值为所辨识的端电压。

(22)

最终选择BLRLS的参数辨识结果作为SOC估计的基础，图9给出了BLRLS的参数辨识结果。表2为两种算法辨识误差对比。可看出BLRLS参数辨识误差更小，辨识结果更优，最终选择BLRLS的参数辨识结果作为SOC估计的基础。

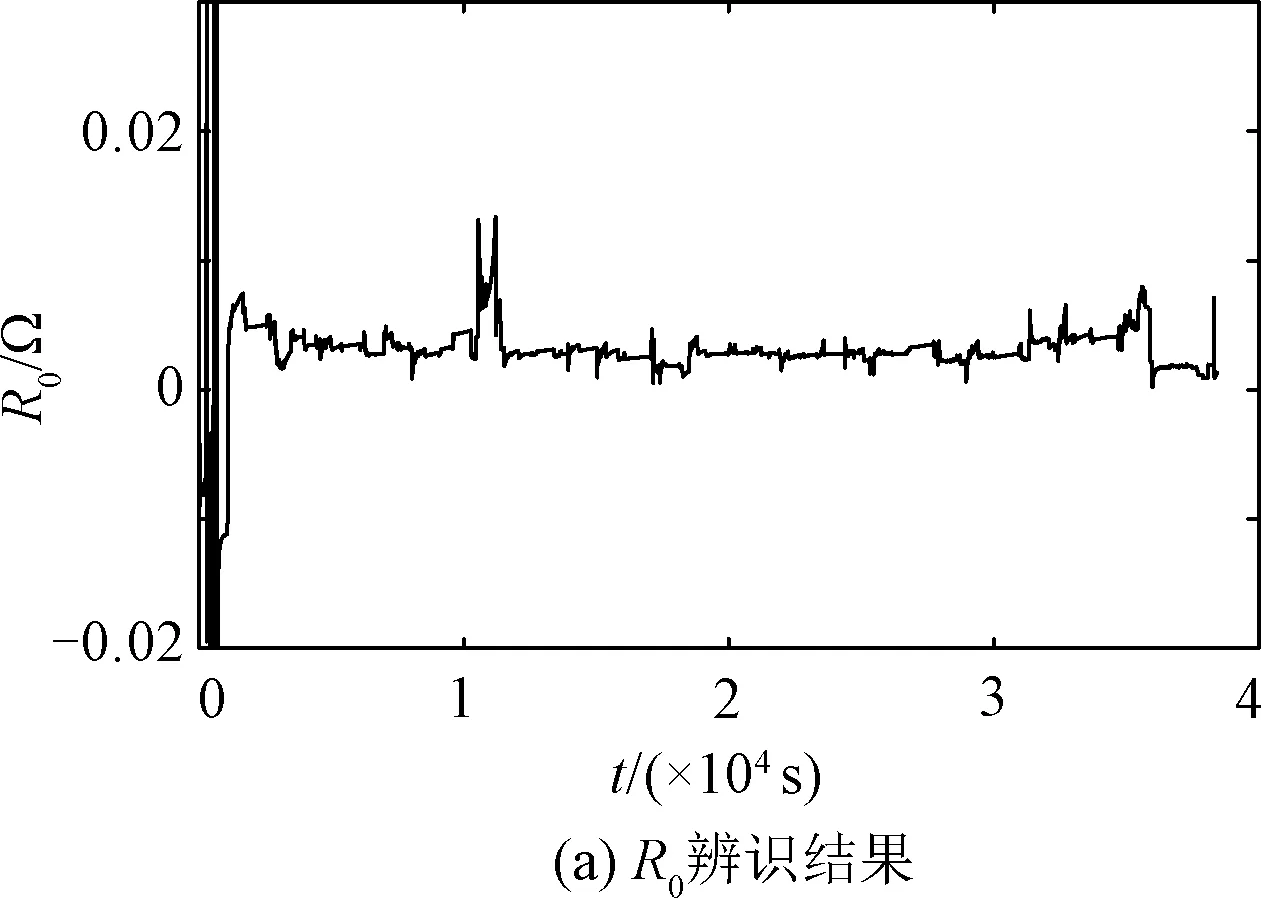
图9 电池参数辨识结果

表2 两种参数辨识算法RMSE和MRE对比

4.3 SOC估计结果验证

本节分别采用间歇恒流放电工况和动态应力测试(Dynamic Stress Test，DST)工况进行此部分的验证。其中间歇恒流放电工况如图6所示，DST工况如图10所示。

图10 DST工况

图11(a)和图11(b)分别为在间歇恒流放电工况和DST工况下，分别采用UKF、SRUKF以及KF-SRUKF算法对电池SOC估计的结果。从图11中可以看出，三种算法均能较准确地实现SOC估计。从图12(a)、图12(b)的SOC估计误差可知，无论是在电流阶跃变化的间歇恒流放电工况下，还是在电流剧变的DST工况下，与其他两种算法相比，采用KF-SRUKF算法能够更准确地跟踪和估计电池的SOC。

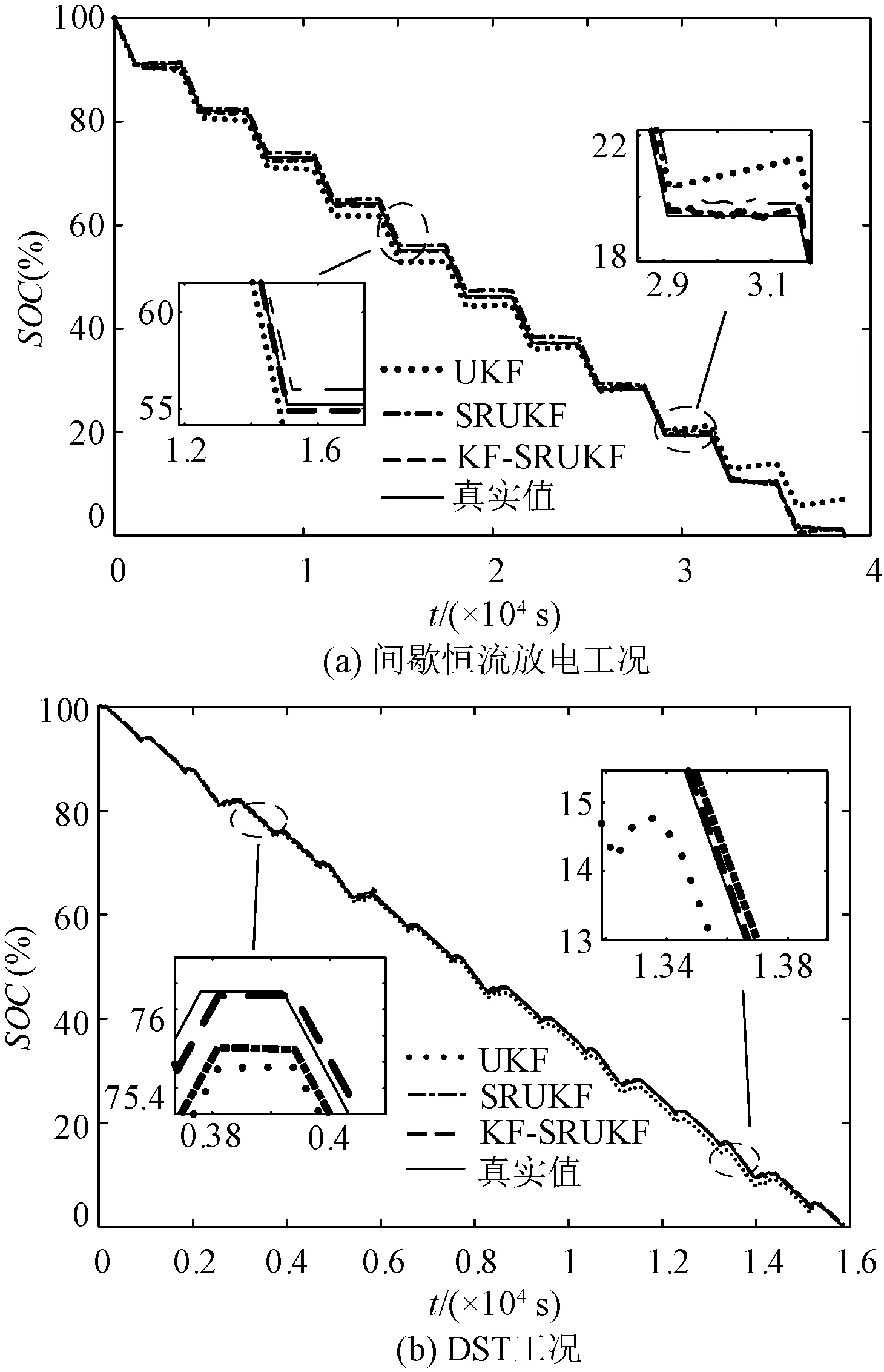
图11 SOC整体估计结果

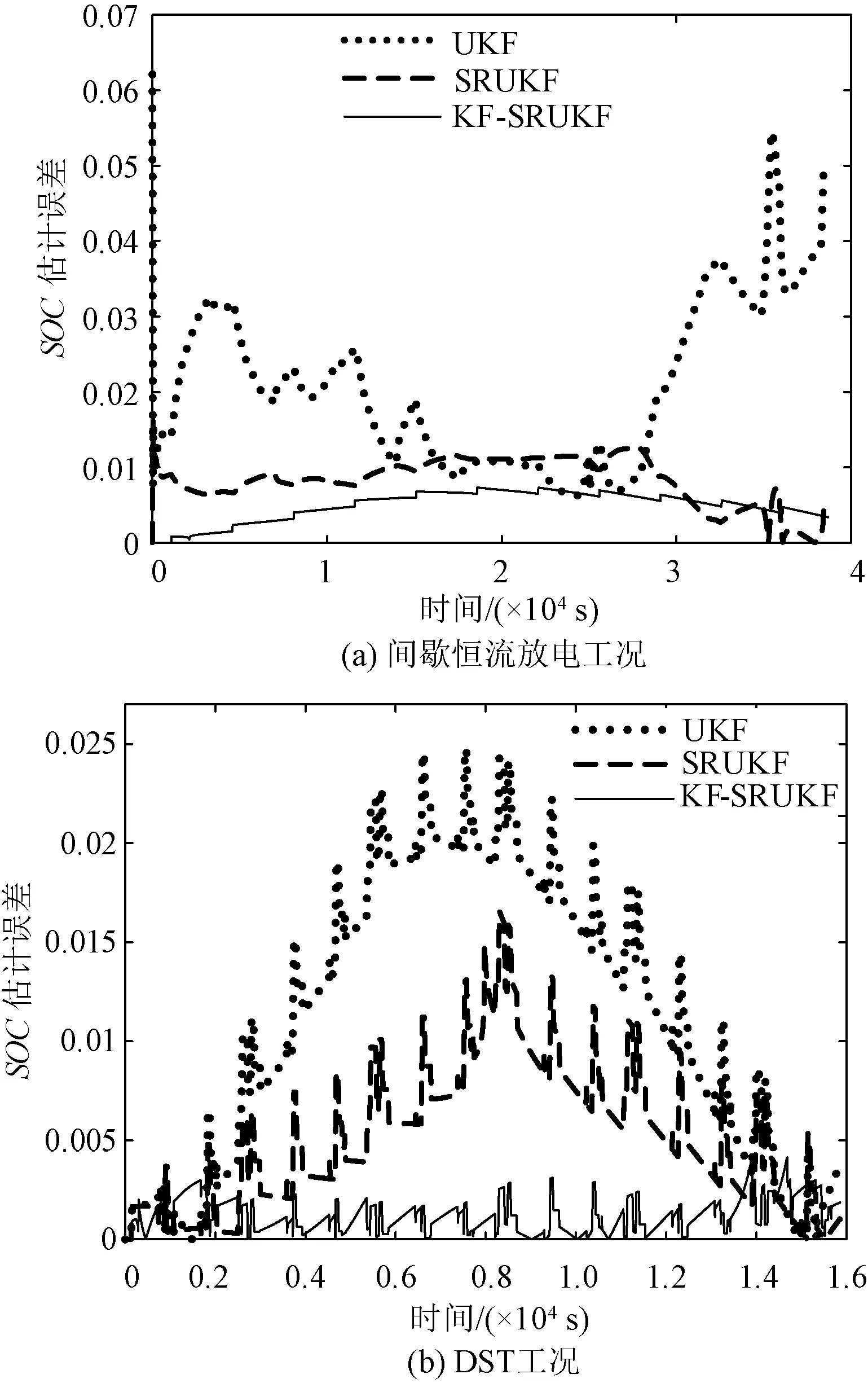
图12 SOC估计误差

表3给出了分别采用UKF、SRUKF和KF-SRUKF算法与BLRLS算法联合进行电池SOC估计时的RMSE和MRE的比较信息，对比表3中数据可以看出：相对于其他两种算法，采用KF-SRUKF算法进行电池SOC估计时，RMSE和MRE数据均有所改善，这表明KF-SRUKF算法可以实现更高精度的SOC估计。

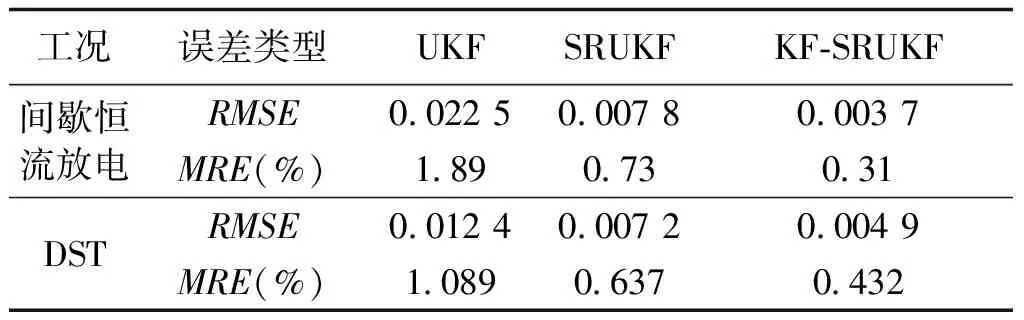
表3 三种算法RMSE和MRE对比

表4为三种算法的平均耗时对比信息，这里计算的是每个采样点在每种算法下的平均耗时。从表4可以看出，使用KF-SRUKF算法的时间最短，说明相较于其他两种算法KF-SRUKF的计算复杂度有所下降，SOC估计效率得到了提高，与理论相一致。

表4 三种算法平均耗时对比

5 结论

本文以锂电池二阶RC电路为基础，将辨识精度更高的BLRLS算法用于模型参数的辨识，针对SRUKF用于电池SOC估计时存在的问题，提出了KF-SRUKF算法。该算法在保证稳定性的基础上，改变了SRUKF对状态方程进行的常规处理，提高了算法的精度，并且减少了不必要的计算量。通过实验结果对比分析表明，所提KF-SRUKF算法相较于已有的UKF和SRUKF在SOC估计精度和速度上均有所提高，体现了所提算法的优越性。