初中几何综合题的解题策略
⦿广西壮族自治区柳州市柳城县教育局教研室 何爱美
1 综合分析法
综合分析法具体是指同时对条件和所求结论进行分析,结合问题所给信息和问题所求进行理解、联想和推导,找到已知条件和问题所求的中间关联点,使已知和未知产生连接.这种同时对条件和问题所求进行分析解题的方法,也被称为“两头凑”.
例1已知AD是圆O的的直径,CE⊥AD于点E,连接AC,过A点任作圆O的弦AB交CE(或其延长线)于点F.
求证:AC2=AF·AB.
分析:如图1,根据已知条件和具体图形如△ACE∽△ADC,可知AC2=AE·AD.

图1
因为需要证明的结论为AC2=AF·AB,所以可转化为证明AE·AD=AF·AB.
2 方程法
方程法就是利用方程的思想来在几何图形中设置未知数沟通已知和未知的关系,然后通过建立方程组求出未知数,最终解决问题的一种思想方法.这种方法在几何类综合题的解题过程中的运用非常广泛.一般来说,能够找到线段、角度之间等量关系的几何问题都可以考虑运用方程法求解.
例2如图2,AB是圆O的直径,C是半圆上一点,圆C切AB于点D,交圆O于点E,F,连接EF交CD于点M.

图2
求证:CM=MD.
证明:设CM=x,MD=y,延长CD交圆O于点G,交圆C于点H,如图3所示.

图3
由垂径定理和切线性质,可得CD=DG.
由相交弦定理,可知
EM·MF=CM·MG=MD·MH.
即x(y+x+y)=y(x+x+y).
故x=y.
即CM=MD.
3 数形结合法
所谓数形结合法,就是同时运用数量关系和具体图象性质解答问题的方法.在几何类综合题解题过程中,主要有以数化形或以形代数两种解题思路.
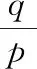

图4

解:由题意可得,线段BE,AE的长度随内接正方形ABCD的位置的变化而变化.
由勾股定理,可得BE2+AE2=p2.
∵BF=AE,
∴BE2+BF2=p2.
又∵BE+BF=q,
∴BE2+BF2=(BE+BF)2-2BE·BF.
即p2=q2-2BE·BF.
实施经济困难老年人家庭适老化改造:2019年,启动经济困难老年人家庭适老化改造试点。2020年末,完成2000户老年人家庭适老化改造。

又∵BE,BF>0,

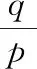
4 化归转化法
化归转化法是指将需要解决的几何问题转化为学生已经学过的问题来解决的方法.这种方法可以化复杂为简单,化抽象为具体,通过研究数学问题解决的本质进行转化,最终解决问题.
例4如图5,已知△ABC的面积为12,BC=6,BC上有一动点P,过点P作PD∥AB交AC于点D,连接PA,假设PB=x,当x为何值时,△PAD的面积有最大值?最大面积是多少?

图5
分析:求S△PAD的最大值,首先根据公式得到关于x的具体表达式.由于△PAD中没有与x有关联的直接条件,故解题的关键在于找出△PAD与PB存在的间接关系,并列出关系式.通过观察可以发现所求三角形面积S△PAD=S△ABC-S△ABP-S△PCD,因此本题可以转化为以下思路求解:
(1)求S△ABP关于x的解析式;
(2)求S△PCD关于x的解析式;
(4)求SPAD有最大值的x的值,并求出面积的最大值.
解:(1)由S△ABC=12,BC=6,可得△ABC的BC边上的高为4,则△ABP中BP边上的高也为4,因此S△ABP=2x.
(2)由PD∥AB,可得△DPC∽△ABC.

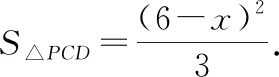
(3)S△PAD=S△ABC-S△ABP-S△PCD
(4)当x-3=0,即x=3时,S△PAD有最大值,△PAD的面积的最大值是3.
例5如图6所示,四边形ABCD内接于圆O,AD=CD,AC交BD于点E.

图6
求证:AD·CD-AE·EC=DE2.
分析:问题需要证明的等式左右两边形式不一致,解题时应考虑化简较为复杂的一边,故首先化简等式的左边.
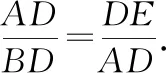
要证明AD·CD-AE·EC=DE2,等价于证明
BD·DE-AE·EC=DE2.
移项可得BD·DE-DE2=AE·EC,即
DE(BD-DE)=AE·EC.
故等价于证明DE·BE=AE·EC.
显然,运用相交弦定理很容易得到这一结论,因此这道题就能得到完整地解决.
总而言之,几何类综合题在中考试卷中所占分值不容忽视,教师应当归纳常见的解题策略以帮助学生灵活应对各种题型,最终提高学生数学学习能力与效率.

