基于不动点理论的二阶微分-积分方程零解的渐近稳定性

朱红英

(广西财经学院 应用数学系，广西 南宁 530003)

100多年来,Liapunov直接法一直是处理常微分方程和泛函微分方程稳定性和有界性最常用的方法。但是, 当方程有无界的项或者时滞是无界的[1-3],或者时滞的导数不小[4],这时利用Liapunov直接法证明微分-积分方程的稳定性问题时就会严重困难。近年来, 多位专家如Becker、Burton等[1-3,5-21]利用不动点定理克服这个困难。而且运用不动点理论解决稳定性等问题还有其他优势[2]。

最近, Burton[6]讨论了下列方程零解的稳定性：

其中L是一个正常数,利用不动点定理得到了每个解x(t)满足(x(t),x(t))→0的充分条件。

Pi[7]研究了带有一个变时滞的方程

得到了在t-τ(t)严格递增前提下方程零解的渐近稳定性。而且要求g(x)满足:存在l>0使得g(x)满足在[-l,l]上的Lipschitz条件;g(x)在[-l,l]上是奇函数和严格单调递增的;x-g(x)在[0,l]上不递减。

2015年, Pi[8]讨论了方程

得到了在t-τ(t)严格递增前提下方程零解的渐近稳定性，并且要求g(x)满足:g(0)=0,g(x)和g(x)-x满足在局部Lipschitz条件, 存在一个正常数L使得

|g(x)-g(y)|≤L|x-y|;∀x,y∈[-l,l]。

讨论一类二阶微分-积分方程

d(t)g′(x(t-τ(t)))x′(t-τ(t))=0

(1)

的渐近稳定性。

方程(1)可写成

(2)

1 定义和引理

定义1若对任意给定的ε>0, 存在δ=δ(ε,t0)，使得当任一φ满足φ(t)∈C(t0)和‖φ‖<δ时, 方程(1)由初始条件φ确定的解(x(t,t0,φ)对一切t>t0均有(x(t,t0,φ)<ε，则称方程(1)的零解是稳定的。

定义2若方程(1)的零解是稳定的, 且存在δ1=δ1(t0)使得φ(t)∈C(t0)和‖φ‖<δ1成立, 则当t→ +∞时, 满足初始条件的解(x(t,t0,φ)均有(x(t,t0,φ)→0。称方程(1)的零解是渐近稳定的。

定理1假设下列条件成立,

成立。

H2:g(0)=0,g(×)满足Lipschitz条件: 对于任意的u、v∈R, 存在一个Lipschitz常数L>0，使得|g(u)-g(v)|≤L|u-v|成立。

H3:当Γ是一个正常数时, 核函数

H4:对于t0≥0连续函数h(s):[t0,+∞)→R有

存在一个常数α∈(0,1)和一个连续函数a(t):R+→R+使得当t≥0,x∈R,y∈R时f(t,x,y)≥a(t),

2 定理1的证明

利用不动点理论证明定理1。首先列出解的表达式。

引理1方程(1)等价于

d(t)g′(x(t-τ(t)))x′(t-τ(t))。

(3)

证明计算方程(2)的第二项得

(4)

(5)

其中

D(s)=

(6)

(7)

注意到

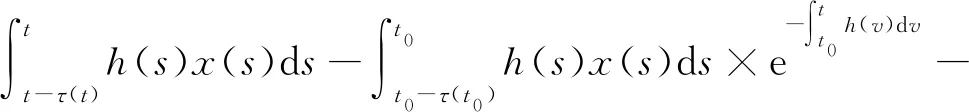
(8)

和

(9)

分步积分得

(10)

并且

(11)

把方程(8)～(11)代入到方程(7), 得到方程(5)。引理2得证。

对于给定的连续初始函数φ, 定义集Cφ⊂C为

Cφ={φ:[t0,∞)→R|φ∈C,φ(t)=φ(t),

t∈(-∞,t0]}

和它的子集

定理1的证明：

(12)

根据A(t)=g(t,x(t),y(t))≥a(t)≥0得

对于给定的ε>0, 存在T1>Q+t0，使得ea0t0- a0T1T1和t0

当t>T1时，得

那么当t→ +∞时，第二项(Pφ)(t)→0。同理, 当t→ +∞时，有I4,I5,I6→0成立。那么

当t→ +∞时,φ(t-τ(t))→0。对于t>T2, 存在一个T2>t0使得φ(t-τ(t))<ε,所以 对于t≥T2有

τ(u))|du+αε。

因此,当t→ +∞时，I15→0。

可以用同样的方法证明当t→ +∞时,方程(12)中其余的项都趋向于零。

如果(x(t),x′(t))是方程(2)的一个解, 其中‖φ‖+x′(t0)|<δ, 那么对任意的t≥t0，有x(t)<ε。注意到当t∈(-∞,t0]时，有x(t)<ε。如果存在t*>t0，使得x(t*)=ε以及当-∞≤s≤t*时,x(s)<ε, 那么根据方程(5)得

容易计算得到

所以x(t*)<ε, 这与|x(t*)|的定义矛盾。因此,

x(t)<ε,∀t≥t0。

(13)

由方程(2)的第二项得

(14)

那么

根据(H1)得

所以

因此, 方程的零解是稳定的,而且证明了当t→ +∞时，有x(t)→0。所以方程的零解是渐近稳定的，完成了充分性的证明。

成立。选择一个正常数ξ, 使得

简记

由条件H4得

于是有

这里β∈R+, 选择一个正整数m足够大，使得

其中δ0>0满足

(1-α)。

当tn≥tm时, 根据方程(5)和|x(t)|≤1，有

(15)

另外,若方程(2)的零解是渐进稳定的,则当t→0时，有x(t)→0。假如当n→∞时,tn-τ(tn)→∞,由中值定理得

显然当tn→∞时,|x(θ)|→0。所以

因此，这与方程(15)矛盾,所以条件H4是方程(2)零解渐近稳定的必要条件。

3 结束语

方程(1)是带有无穷时滞的二阶微分方程，如果使用李亚普诺夫直接法来研究方程(1)的零解的渐近稳定性，那么无穷时滞项只能限定为有界，所以实际上不能使用最常用的李亚普诺夫直接法来证明这类方程零解的稳定性。而本文利用不动点定理,得到了方程(1)零解渐近稳定的充分必要条件。总之，不动点定理不仅解决了方程的零解的渐近稳定性问题,其结果解除了以往对无穷时滞的严格限制,而且也明显减少对函数g的限制。不动点定理可用来研究带有无界的项或者无穷时滞的微分方程零解的渐近稳定性问题，当然这里的不动点不局限于Banach不动点定理，还可以是Krasnoselskii不动点定理、Shauder不动点定理等等。