基于晶格Boltzmann方法的CUDA加速优化

张乾毅， 韦华健， 赫轶男， 李华兵

(桂林电子科技大学 材料科学与工程学院，广西 桂林 541004)

随着处理器时钟频率极限及“功耗墙”等问题的出现，单核解决方案被摒弃，基于多核架构的图像处理单元(GPU)逐渐出现在人们的视野中。2007年，英伟达公司为GPU增加了一个易用的编程接口——统一计算架构(compute unified device architecture，简称CUDA)[1]。它以标准C为基础进行扩展，使程序员可以在C、C++及Fortran等开发环境进行并行程序编写，将利用GPU进行并行计算的门槛大大降低。近年来，人工智能在深度学习的不断推动下高速发展，这离不开GPU的强大计算能力和优秀的GPU编程环境。CUDA技术已经获得广泛关注，并被应用到流体力学、生物计算、气象分析、金融分析等众多领域。

晶格玻尔兹曼方法(LBM)是一种介观尺度的模拟方法，在流体力学方面的模拟中被广泛应用，如多孔介质流[2]、血液流[3]、多相流[4]淋巴流[5]等。LBM物理背景清晰，易于并行计算，边界条件处理简单，因而十分适用于大规模GPU并行计算。如Tölke等[6]使用CUDA实现了LBM多孔介质流动模型的计算加速。郑彦奎等[7]实现了LBM方腔模型的计算加速。

鉴于此，通过线性寻址和下标寻址方法实现了LBM模型中的泊松流算例。将程序分别用CPU和GPU进行计算，比较2种寻址方法分别在2种处理单元上的计算时间，并算得加速比。

1 GPU与CUDA

基于设计目标的差异，GPU在设备架构上与CPU存在很大区别。CPU需要很强的通用性来处理各种不同的数据类型，同时逻辑判断又会引入大量的分支跳转和中断处理。因此，CPU中分布着多样的计算、控制单元和占据大量空间的存储单元。而GPU的设计主要是用来解决大量逻辑上相对简单的任务，因而GPU采用了数量众多的核心和算术逻辑单元(ALU)，其数量远超CPU，通常CPU的核心数不会超过2位数，但GPU只配备了简单的控制逻辑和简化了的存储单元。

CUDA编程模型将CPU作为主机端，GPU作为设备端，二者各自拥有相互独立的存储地址空间：主机端内存和设备端显存。一个典型的CUDA程序包括并行代码和与其互补的串行代码。由CPU执行复杂逻辑处理和事务处理等不适合数据并行的串行代码，并调用GPU计算密集型的大规模数据并行计算代码，即内核函数。当设备端开始执行内核函数时，设备中会产生大量的线程，线程是内核函数的基本单元，负责执行内核函数的指定语句[8]。CUDA程序模型如图1所示，由一个内核启动所产生的所有线程统称为一个线程网格，同一网格中的所有线程共享相同的全局内存空间。一个网格又由多个线程块构成，同一线程块内的线程协作可通过同步和共享内存的方式实现，不同块内的线程不能协作。每个GPU设备包含一组流多处理器(SM)，一个SM又由多个流处理器(SP)和一些其他硬件组成。CUDA程序执行过程中会把线程块中的所有线程以线程束(Warp，含32个线程)为执行单位分配给SM中的不同SP来进行计算。

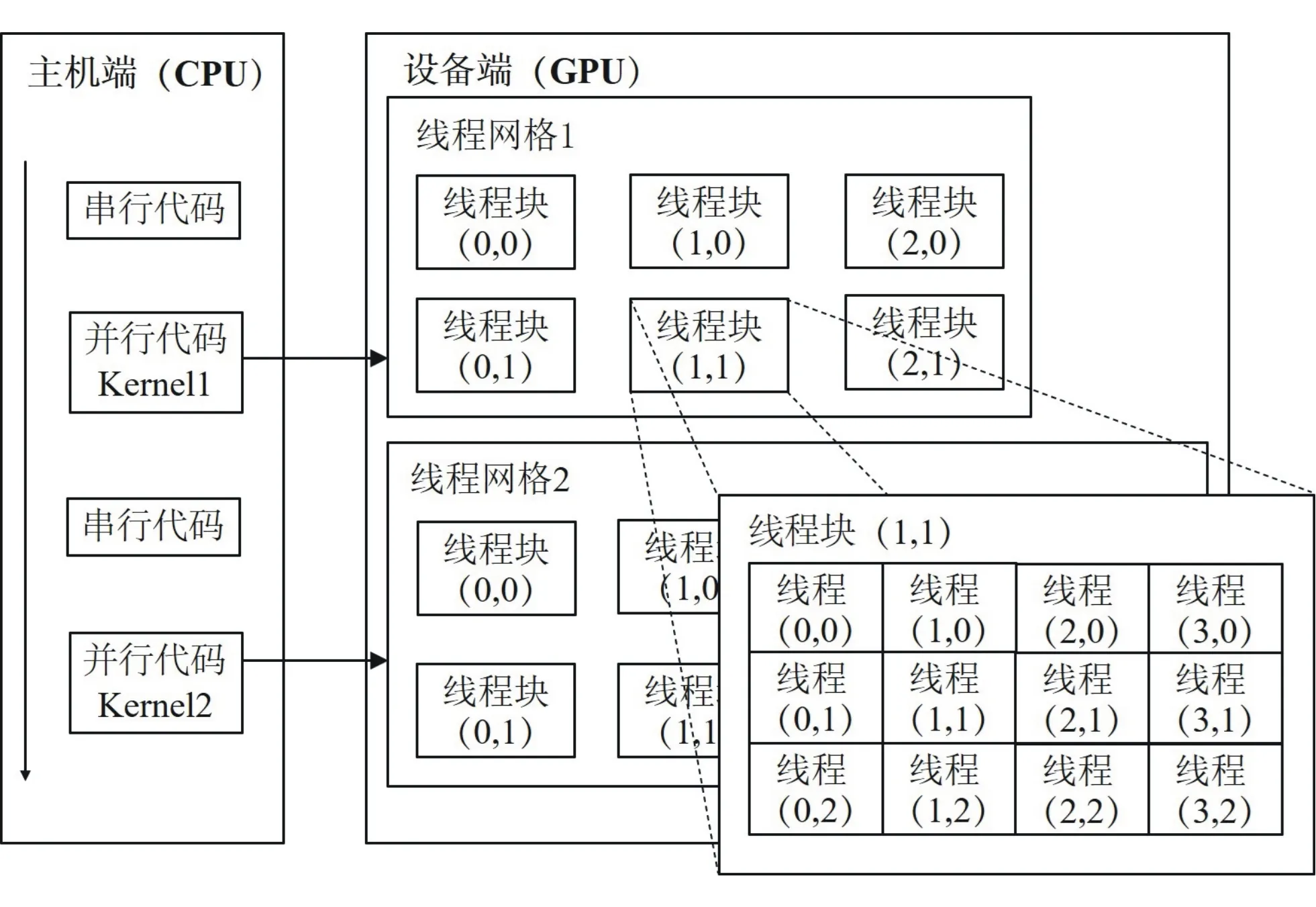
图1 CUDA程序模型

GPU采用了内存分层架构，并通过多级缓存机制来提高读写效率。CUDA内存模型如图2所示，GPU中主要的内存空间包括寄存器、共享内存、全局内存、常量内存、纹理内存和本地内存。每个SM都拥有独立的一级缓存，所有SM共享二级缓存。GPU致力于为每个线程分配真实的寄存器，当寄存器使用到达上限时，编译器会将数据放在片外的本地内存中。共享内存是可受程序员控制的一级缓存，每个SM中的一级缓存与共享内存公用同一个内存段[9]，它仅对正在执行的线程块中的每个线程可见。

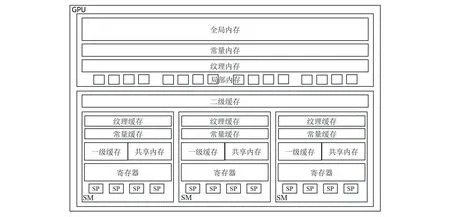
图2 CUDA内存模型

2 晶格玻尔兹曼方法(LBM)

McNamara等[10]用单粒子分布函数fi取代了格子气细胞自动机中的布尔变量，其LBM演化方程为

fi(x+eiδt,t+δt)-fi(x,t)=Ω(fi)，

(1)

其中：i为微观速度的索引，对于D2Q9模型，i取值1～9；fi(x,t)为在x位置t时刻具有ei速度的粒子的分布函数；δt为时间增量；Ω(fi)为碰撞因子，表示碰撞对于fi的影响。文献[11-13]采用单弛豫时间来替代碰撞因子项。继而，LBM方程可写为

(2)

其中：fi(eq)为局域平衡分布函数；τ为弛豫时间。求出粒子分布函数后，则宏观密度、流体的流速分别为

(3)

(4)

采用图3所示的D2Q9模型(D指维度，Q指粒子运动方向总数)模型[14]进行计算，其平衡分布函数具体定义为

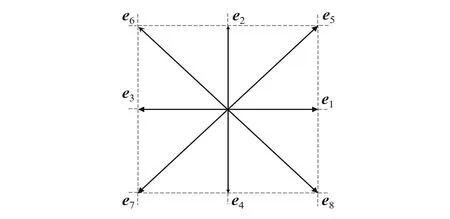
图3 D2Q9模型

(5)

其中：c为基准速度，通常情况下取1；ωi为各方向的权重系数。当i=0时，ωi=4/9；当i=1,2,3,4时，ωi=1/9；当i=5,6,7,8时，ωi=1/36。ei的形式为

3 算法实现及优化

一个典型的LBM计算案例主要分为3个步骤：1)声明变量并进行分布函数的初始化；2)进行格点的碰撞、迁徙流动和边界处理，并进行宏观量的计算；3)进行稳定性条件判断，决定是否结束步骤2)的迭代。由文献[15]知，步骤2)的迭代计算占整个计算时间的98%，因此该步骤应在GPU上进行并行加速。本计算以淋巴管为物理背景，将淋巴管内流动的淋巴液视作等截面圆形管道内的泊松流，进行模拟计算。尝试用线性寻址和下标寻址2种不同的寻址方法进行计算，比较这2种寻址方法分别在GPU与CPU上执行计算时间的差异。

3.1 线性寻址程序设计

LBM的基本变量是分布函数，进而由分布函数计算求得格子点的密度和x、y方向上的速度等宏观量。在串行程序的D2Q9模型中，分布函数通常被设为三维数组df[i][j][k]并存储在主存中，i、j表示整个线程网格中格点的坐标(0≤i≤width，0≤j≤height；width、height均为固定值，分别表示线程网格的宽度和高度)，k为格点运动方向数，k=0,1,…,8。

在设备端声明指针double*df，调用cudaMallocManaged()函数在设备端开辟大小为width*height*9*sizeof(double)的一维线性内存空间，用于存放每个格点上9个方向的分布函数，并将在显存上获得的内存空间首地址赋值给df。使用cudaMallocManaged()函数开辟的存储空间，无论是在串行代码中还是并行代码中，都可使用这块内存，因此只需定义一个指针即可在主机和设备端通用。继续开辟多个设备端内存空间，用于存放其他计算变量的数据。指针double *dd指向存储格子点密度的内存空间，指针double *dvx、*dvy分别指向存放x和y方向上速度的内存空间。

基于上述在全局内存中使用三维数组来储存分布函数及其他变量的方式，设计了3个在CPU端执行的collide()、stream()、calculate()函数，分别代表格点的碰撞、迁徙流动和宏观量的计算等步骤，并将其命名为方案一。方案二则是将迭代计算过程放在GPU端并行执行，对应设计了addKernelCollide()、addKernelCopy()、addKernelStream()、addKernelCalculate()四个内核函数来实现。相较于方案一中执行各个步骤都需要嵌套for循环来遍历读写每个格点上的数据，方案二则通过内核函数用GPU映射出大量线程，同时对每个格点数据进行操作。

首先，调用cudaMallocManaged()函数，在GPU端为分布函数、密度等变量开辟内存空间，再定义一个parameter结构体，为之后格子点迁徙流动做铺垫。对4个内核函数进行如下讨论：

1)碰撞步：启动addKernelCollide<<>>(df,iSol,…,dev_p)内核函数，其中grid为线程网格中线程块数，将其设为width；block为每个线程块中的线程数，设为9*height；iSol为用于判断格点是否位于边界上的变量；dev_p为parameter结构体变量。声明变量i、j、k并赋值，i=blockIdx.x，j=threadIdx.y，k=threadIdx.x。在函数体内分别计算出线程访问分布函数一维数组的下标索引id=adr(i,j,k)=k+(j+i* height)*9和其他变量的下标索引ind=adr(i,j)=j+i* i*height。通过一次if判断，保留格子边界以外的所有格子点进行计算，每个线程利用式(2)计算对应格子点的分布函数：

df[id]=df[id]-(df[id]-

feq(k,dd[ind],dvx[ind],dvy[ind]))/Tau。

feq()为平衡分布函数，Tau为弛豫时间。

2)流动迁徙步：启动addKernelCopy<<>(df,dfbak)内核函数，声明变量并赋值，计算出线程访问的下标索引，方法同上。将df[id]中的数据传递给dfbak[id]。启动addKernelStream<<>>(df,dfbak,iSol,…)内核函数，将dfbak[id]的值赋给df[id]，此时dfbak[id]中

id=k+[(j-dev_Prjy[k])+(i-

dev_Prjx[k])*height)]*9。

3)计算宏观量步：启动addKernelCalculate<<>>(df,iSol,…)内核函数，声明变量并放入共享内存中。

__shared__ double sdf[9];//9个分布函数

__shared__ double ddd;//格子点密度

__shared__ double vx;//x方向速度

__shared__ double vy;//y方向速度

……

for(k=0;k<9;k++)

{

sdf[k]=df[adr(i,j,k)];

}

利用sdf[k]计算得到ddd、vx、vy的值，最后将共享内存中的数据传回主存中。

3.2 下标寻址程序设计

基于之前的线性寻址方法对程序做以下修改。

1)声明指针double *df0、double **df1、double ***df，在GPU上开辟3个内存空间，并将首地址分别赋值给df0、df1、df，具体操作如下：

cudaMallocManaged(void(**)&df0,width*height*9*sizeof(double));

cudaMallocManaged(void(**)&df1,width*height*sizeof(double*));

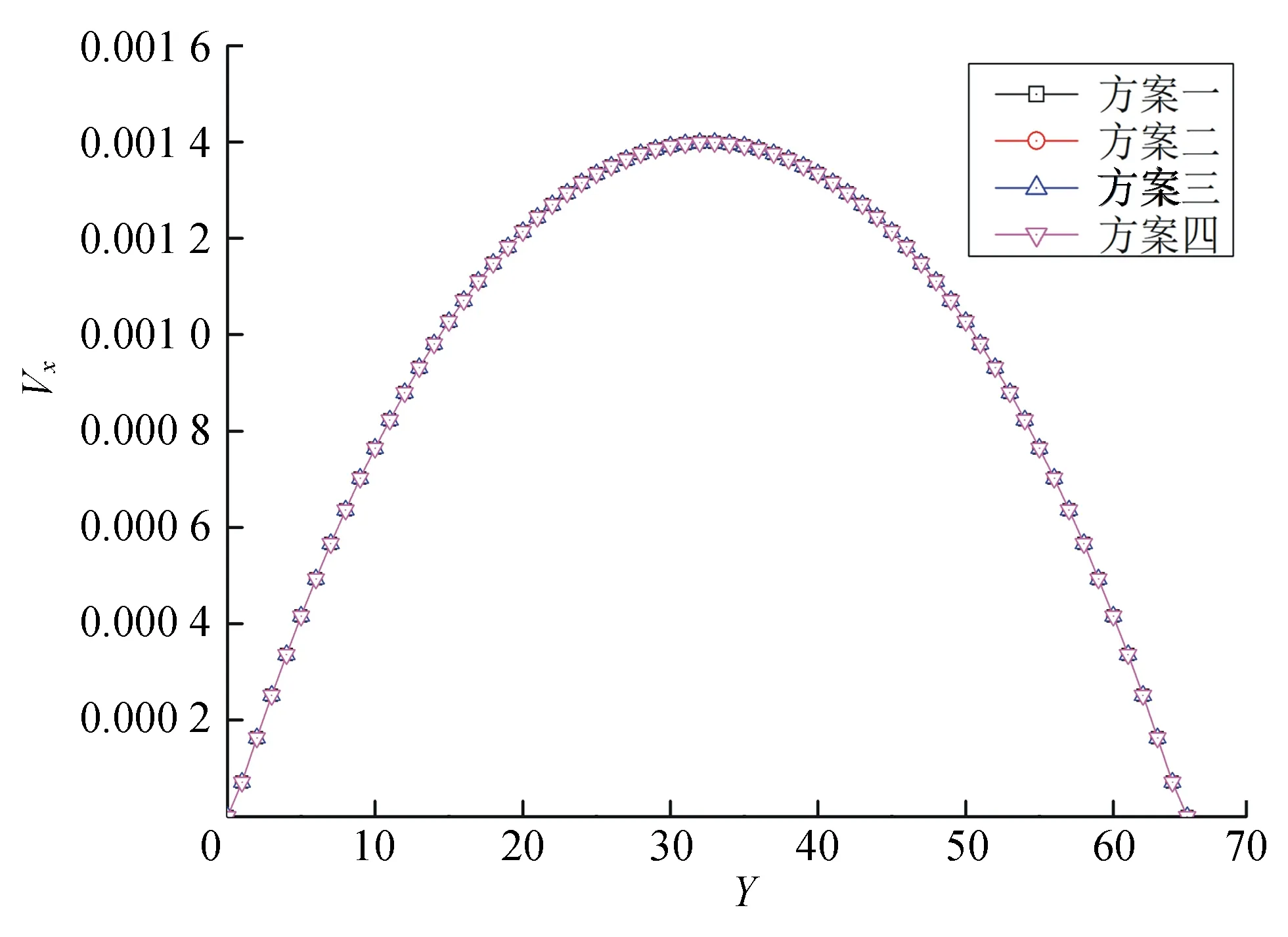
for(i=0;i

{

for(j=0;j

{df1[i*height+j]=&df0[(i*height+j)*9];}

}

cudaMallocManaged(void(**)&df,width*height*sizeof(double**));

for(i=0;i

{df[i]=&df1[i*height];}

2)声明指针double *dd0、double **dd，在GPU上开辟2次内存空间，并将首地址分别赋值给dd0、dd，具体操作如下：

cudaMallocManaged(void(**)&dd0,width*height*sizeof(double));

cudaMallocManaged(void(**)&dd,width*sizeof(double*));

for(i=0;i

{dd[i]=&dd0[i*height];}

3)其他宏观量修改方法同上。

在各计算步骤中，用多维数组表示不同格点位置上的分布函数和其他宏观量，形如df[i][j][k]、dd[i][j]、dvx[i][j]、dvy[i][j]。将方案一、二按上述内容进行修改，并分别命名为方案三、四。

4 计算结果分析

采用含有8个Nvidia Quadro GP100显卡集群的服务器完成计算，GP100显卡拥有3 584个CUDA并行计算处理核心，处理双精度浮点数的能力为5.2 TFlop/s，搭配16 GiB HBM2显存，理论带宽高达717 GiB/s。同时服务器搭载了Intel(R) Xeon(R)CPU E-52620 v4处理器，核心数为8个，主频为2.1 GHz，编译环境为CUDA10.0，运行环境为Linux Ubuntu。

表1 4种泊松流模拟方案运行时间

以平面泊松流为算例，在保证计算结果正确性的前提下验证2种寻址方法对程序计算时间的影响。图4为4种方案迭代4 000步时的模拟结果，4种方案结果一致，表明了程序修改的正确性。表1为迭代4 000步时，4种方案模拟的计算时间。从表1可看出，基于线性寻址方式的方案一、二，GPU相对CPU的加速比约为71倍，而基于下标寻址方法的加速比只有约25倍；方案一、三都用CPU完成迭代计算步，方案三的计算时间减少了将近三分之二，因而使用下标寻址的方式更适合CPU端的迭代计算；方案二、四计算时间无太大变化，表明下标寻址对GPU端的并行计算无明显帮助。

图4 4种泊松流模拟方案结果

5 结束语

采用CUDA实现了LBM的泊松流算例。设计了线性寻址、下标寻址2种寻址方法，并实现了这2种寻址方法分别在主机端和设备端上的4种LBM计算方案。4种方案计算结果一致，表明了程序设计的正确性。用线性寻址方法获得了71倍的加速比，表明用CUDA对LBM计算效率的提升有很大帮助，也展现了GPU在大规模科学计算中的巨大潜力。