基于0 -1整数规划模型的校园公交系统优化方案——以桂林电子科技大学为例

魏 睿， 李凤媛， 李科赞， 葛志金

(桂林电子科技大学 数学与计算科学学院，广西 桂林 541004)

随着我国高等教育的普及，每年的大学招生规模也在不断扩大，许多大学校园在不断地扩建，出现了教学设施分布较散的现象。随着校园规模的扩大，教学区与宿舍区、食堂、运动区之间的距离增大，老师和学生步行上下课路途远、耗时长，为校园出行带来不便。许多同学有了自己的电动车，方便自己的同时也易发生交通事故，同时给校园交通造成一定的压力，乱停乱放也给学校的管理带来一定的考验。

为了缓解校园交通压力，给师生带来便利的出行方式，许多学校引进了校园公交系统这种集约化的公共交通方式[1-3]。虽然现在有许多文献对校园公交的运营及规划有一定的研究和探讨，但大部分内容都缺少理论知识，未给出实际的设计算法。鉴于此，以桂林电子科技大学校园为例，采用0-1规划和蚁群算法，针对目前仍存在一些公交站点、公交线路规划不合理，学生使用体验感差以及使用率低等缺陷，对公交线路、公交站点等进行优化，使得优先资源最大化使用，给师生带来最大方便的同时，创造一个节约型校园出行新方式。

1 校园公交系统现状

1.1 校园环境现状

本次研究以桂林电子科技大学花江校区为例，校园地图如图1所示。

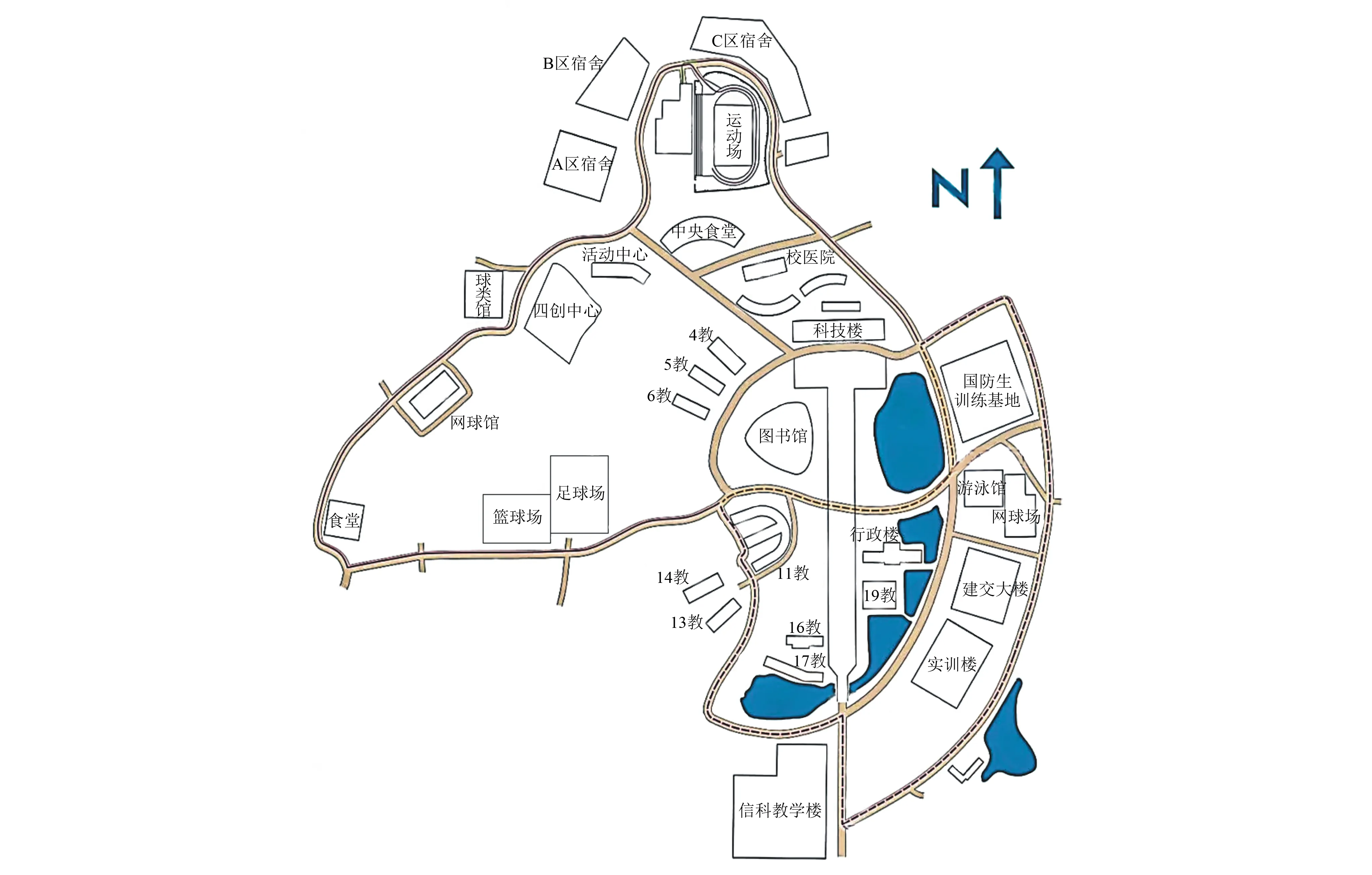
图1 桂林电子科技大学花江校区校园地图

花江校区校园面积较大，现有师生25 000人左右。校园仍有许多区域等待开发，目前有多栋教学楼、多个宿舍区、图书馆、篮球场、足球场、食堂等，分布较散，道路复杂交错，对于师生出行产生不便。桂林每年雨季较多，校园易产生积水，这也是一种出行障碍。

该校区也引进了校园公交，但是目前运营模式不稳定，没有固定公交站点，没有固定的运行时间，且只有2条公交线路，这些导致了学生不清楚公交运营状况，使用率低下。公交司机也不能掌握学生上下课分布情况，仅凭经验运行，有时公交数量分布不均，浪费了有限资源。

1.2 学生出行现状调查

为了解学生的基本出行现状，对不同年级进行分层抽样，调查结果表明，44%的同学选择步行，31%的同学使用共享单车，19%的同学使用电动车，6%的同学使用校园公交等其他方式。同时对学生校园公交使用意愿进行调查，有60%的同学比较愿意采用校园公交的出行方式，由此可见，校园公交在校园内还是有很大的市场有待发掘。

2 公交站点设计

2.1 数据整理

对校园内主要的教学楼、宿舍区、路口等进行编号，编号数据如表1所示。通过实地测量，得到各个编号之间的实际距离，如表2所示。根据表1和表2数据得到校园各地点编号及路线分布图，如图2所示。

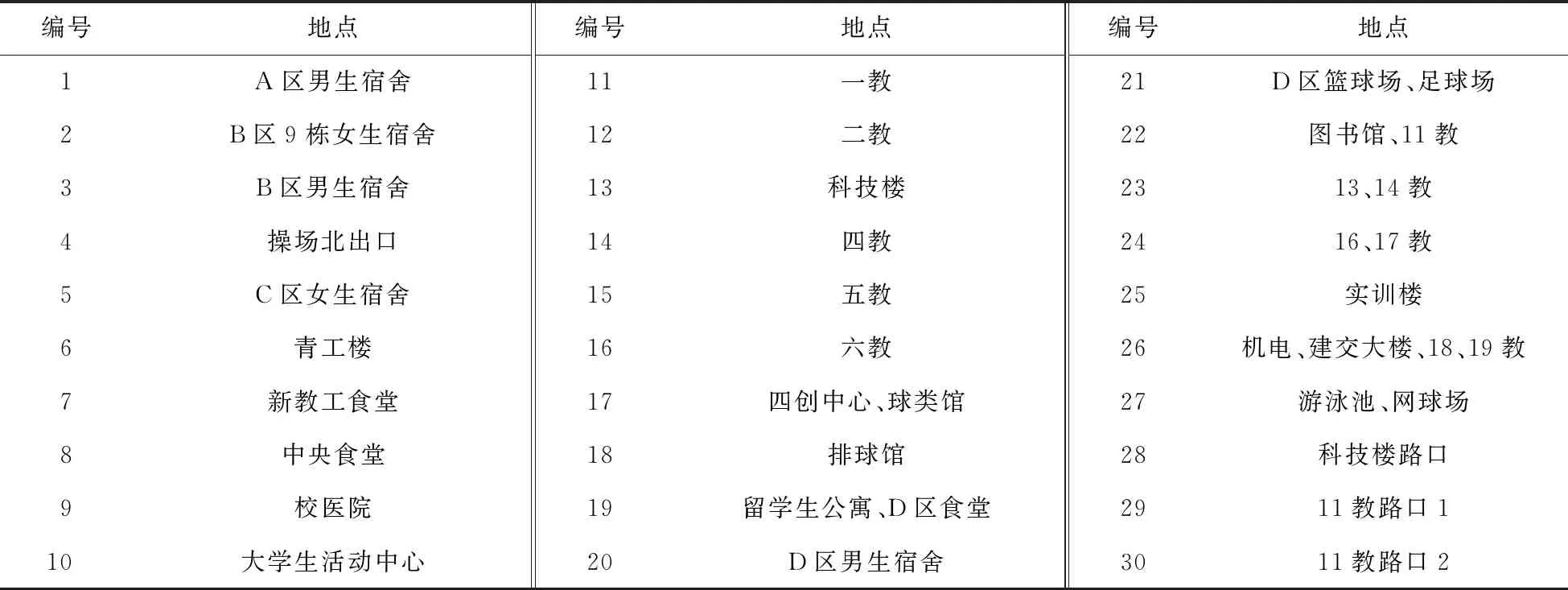
表1 校园主要地点部分编号

表2 各编号之间直线距离

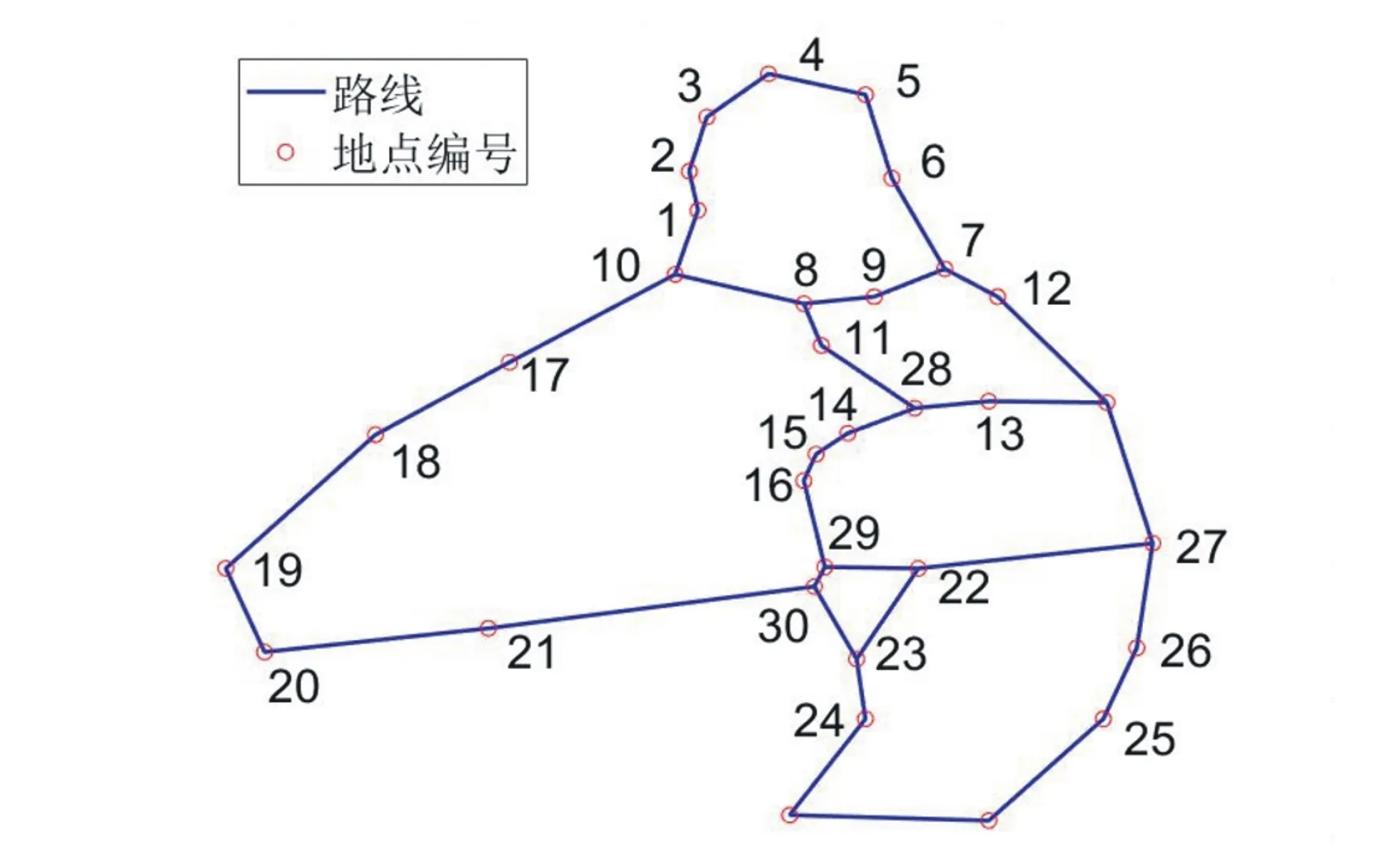
图2 校园主要地点编号及路线图

2.2 0 -1整数规划模型

公交站点设计需要考虑师生的出行是否便利，一般情况下，如果师生想去某个地点，那么这个地点就需要设置成站点，这是最优方案。但在实际中，有些地点距离很近，这样设计会使得资源浪费，因此应该尽量设计较少的公交站点，达到最优的公交站点覆盖范围。根据调查，大部分学生可以接受的目的地到公交站点距离范围在100 m以内，故以100 m作为公交站点最大的覆盖范围进行研究。此问题是一类选址问题，需建立0-1整数规划模型[4]，根据各个地点之间距离的情况，安排尽可能少的公交站点，实现最大的区域覆盖。

首先通过Floyd算法[5]更新各个地点到其他地点之间的最短路线。在此基础上，判断公交站点能否同时覆盖这些地点。以设置最小的公交站点为目标函数，即

(1)

其中，

假设各个地点之间的最短距离为dij，zij表示在i地建立公交站，能否覆盖点j，若可以覆盖，则zij=1，否则zij=0。 由此可得以下约束条件：

(2)

将实际测量数据代入式(2)进行求解，得到所需建立数量最少时的站点为1、4、5、6、9、10、15、17、18、19、20、21、22、23、24、26、27、28、30。以这19个站点作为拟定公交站点，示意图如图3所示。

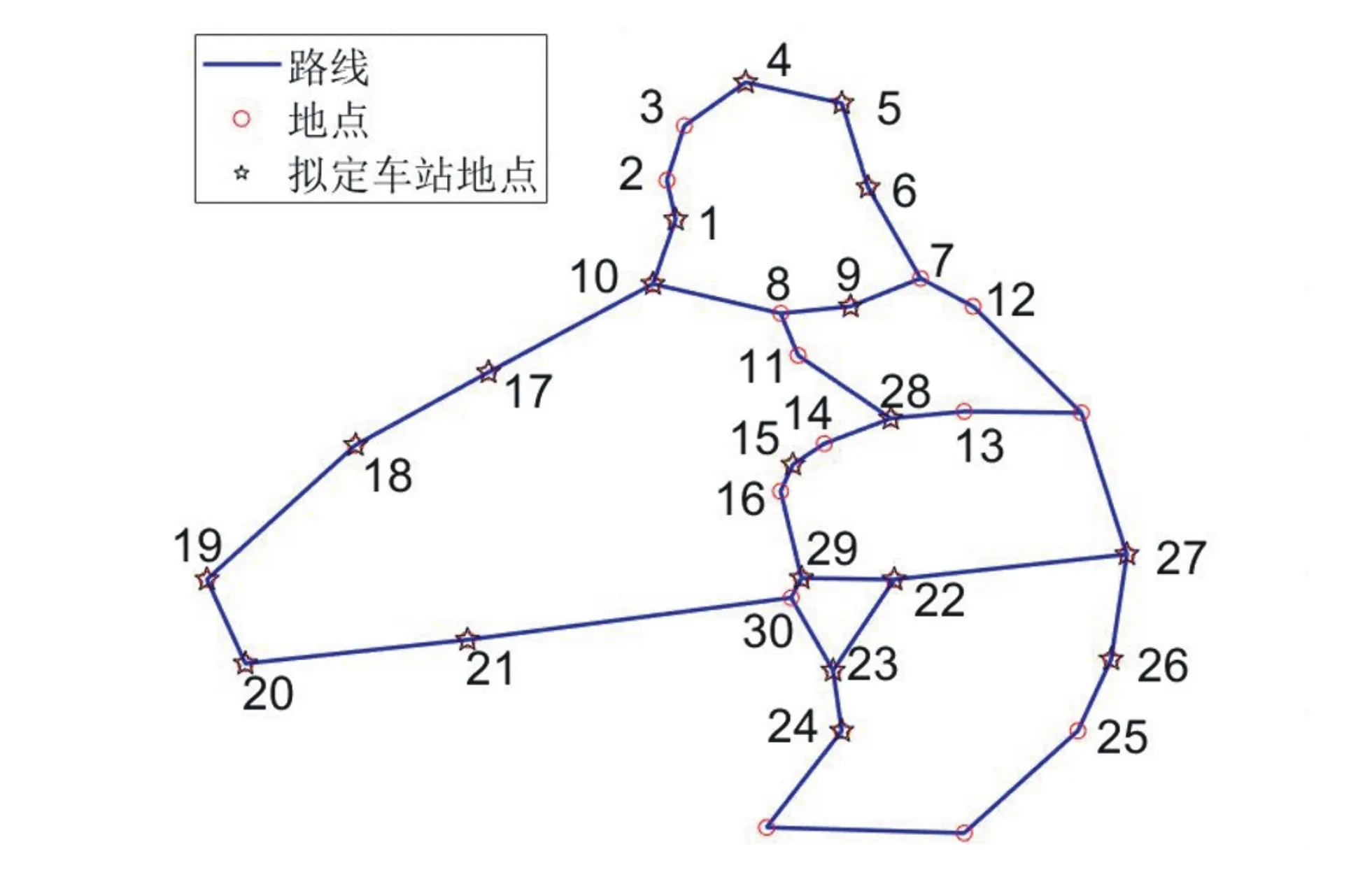
图3 拟定公交站点示意图

3 公交路线最优规划

按上述问题求解的结果对公交线路进行规划，最佳公交线路是每个站点都要经过且只经过一次的最短路径，由此可将此问题转化为一个旅行商(TSP)问题。旅行商问题就是从一个点出发，找出一条可以经过所有点且每个站点只经过一次的最短回路。目前对于旅行商问题的求解有许多方法，贪心算法是其中一种，但是这种方法只能求解局部的最优解，对于全局来说很难得到最优解[6]。

蚁群算法作为一种智能算法在旅行商问题上有很好的应用，有许多成功案例[7-8]。蚁群算法的基本原理来源于自然界中蚂蚁觅食的最短路径原理，蚂蚁在寻找食物源时，在其走过的路径上释放一种蚂蚁特有的信息素，使得在一定范围内的其他蚂蚁可以察觉到并由此影响它们后续的行为。当一些路径上通过的蚂蚁越来越多时，其留下的信息素也越来越多，以致信息素强度增大，蚂蚁选择该路径的概率也越高，从而更增加了该路径的信息素强度，这种选择过程被称为蚂蚁的自催化行为。

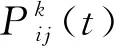
(3)

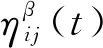
在遍历各地点的过程中，蚁群释放信息素的同时，各地点之间连接路径上的信息素的强度也在通过挥发等方式逐渐消失。为了描述这个特征，设ρ为信息素挥发程度。所有蚂蚁走完一遍所有地点后，各个地点连接路径上的信息素浓度为

(4)

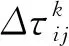
一般情况下，

(5)

其中：Q为信息素常数；Lk为第k只蚂蚁经过的路径总长度；ij表示从地点i到地点j的路径。

蚁群算法流程如图4所示。

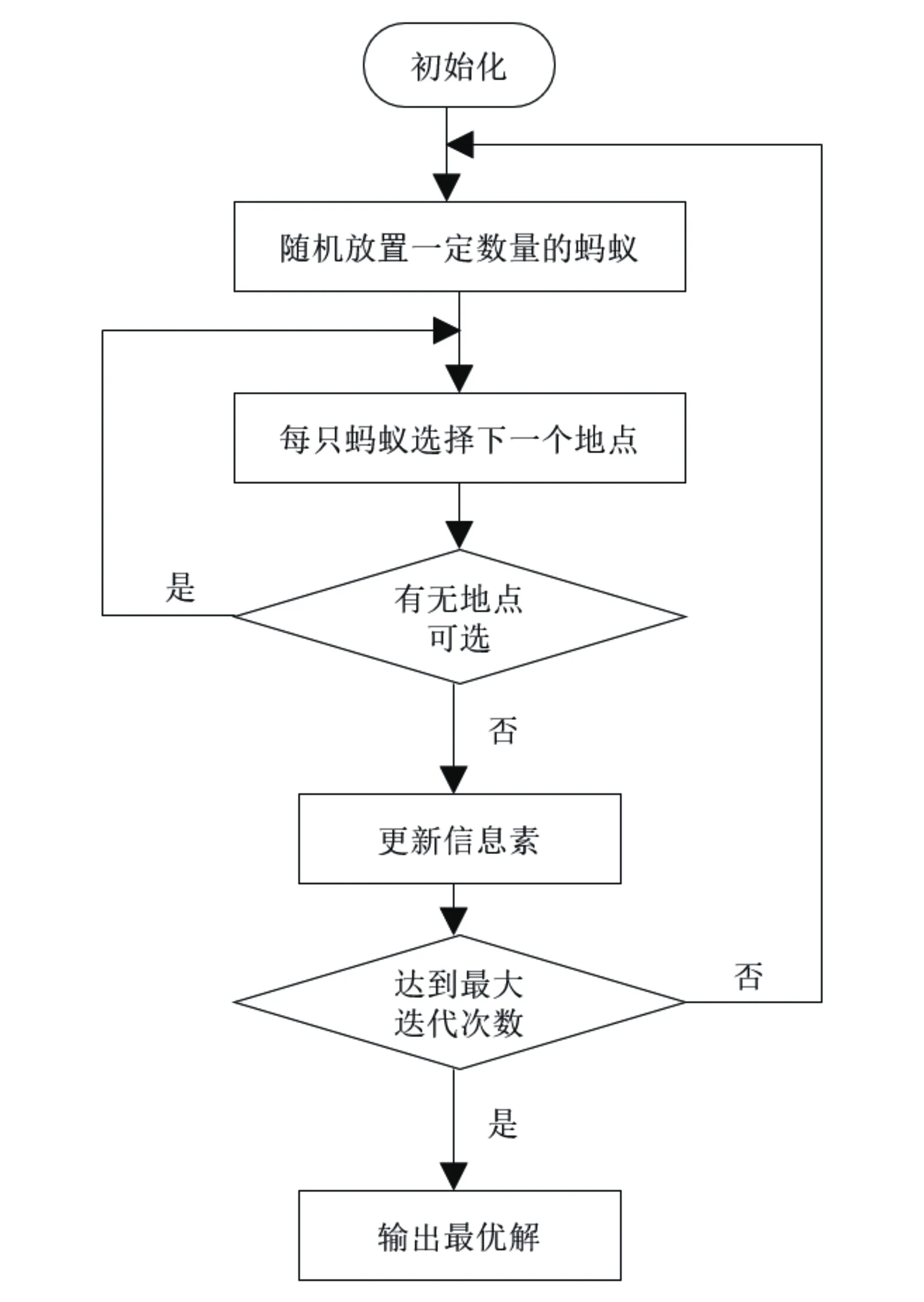
图4 蚁群算法流程图

根据表2数据可得各地点之间的距离情况，在蚂蚁数为50，最大迭代次数为500时，蚁群算法求得的距离最短路线如图5所示。

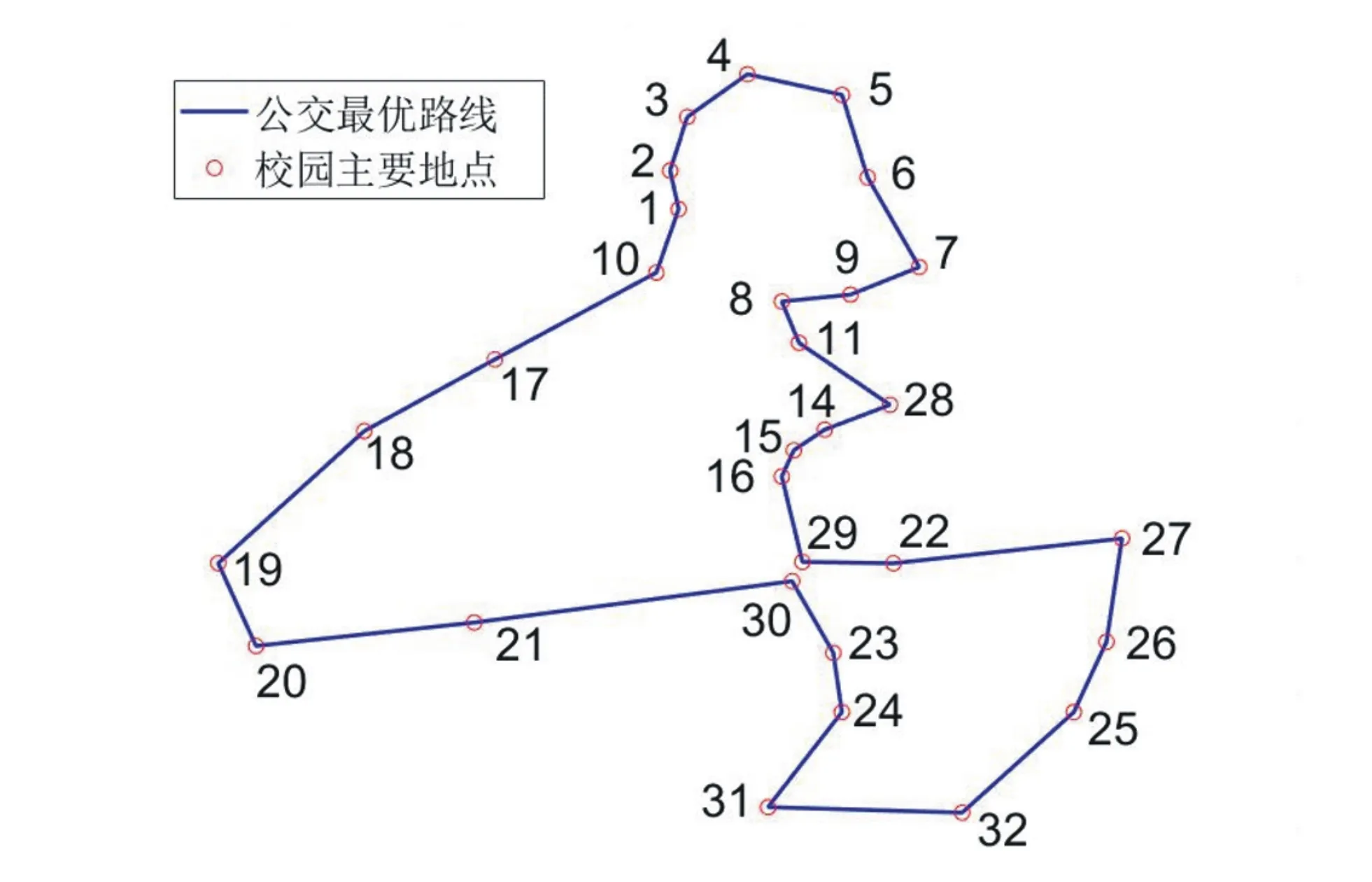
图5 蚁群算法所求的最佳路线

图5中路线产生的最短回路长为4 805 m。在校园内车辆行驶速度不超过20 km/h的情况下，至少需要15辆车才可以满足大多数学生时间上的需求。

4 公交系统仿真模拟实验

为了解公交系统实际的载客及运输能力，对公交系统进行了模拟实验。目前每辆车最大可供40人同时使用，公交到达每个站点都会有人上车，有人下车，这些都是随机的。

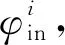
(6)

其中：Ni为当前站点一分钟内的人流量；p为学生愿意乘坐公交的比例，根据之前的调查可将其定为

为愿意乘坐公交的学生真正上车的概率。

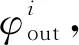
(7)

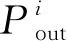
同时要求上车人数跟车内总人数不能超过40人，下车人数不能使车内人数低于0，此时每辆公交车在行驶一圈后，整个过程所搭载的乘客数量为

(8)

为了解学生上下课时主要分布及各地点的人流量大小，按不同时间段对所有地点进行统计，得到每分钟各地点人流量，如表3所示。将表3数据代入式(6)～(8)，得到一辆公交车绕行校园一圈所能搭载的人数模拟数据，如表4所示。

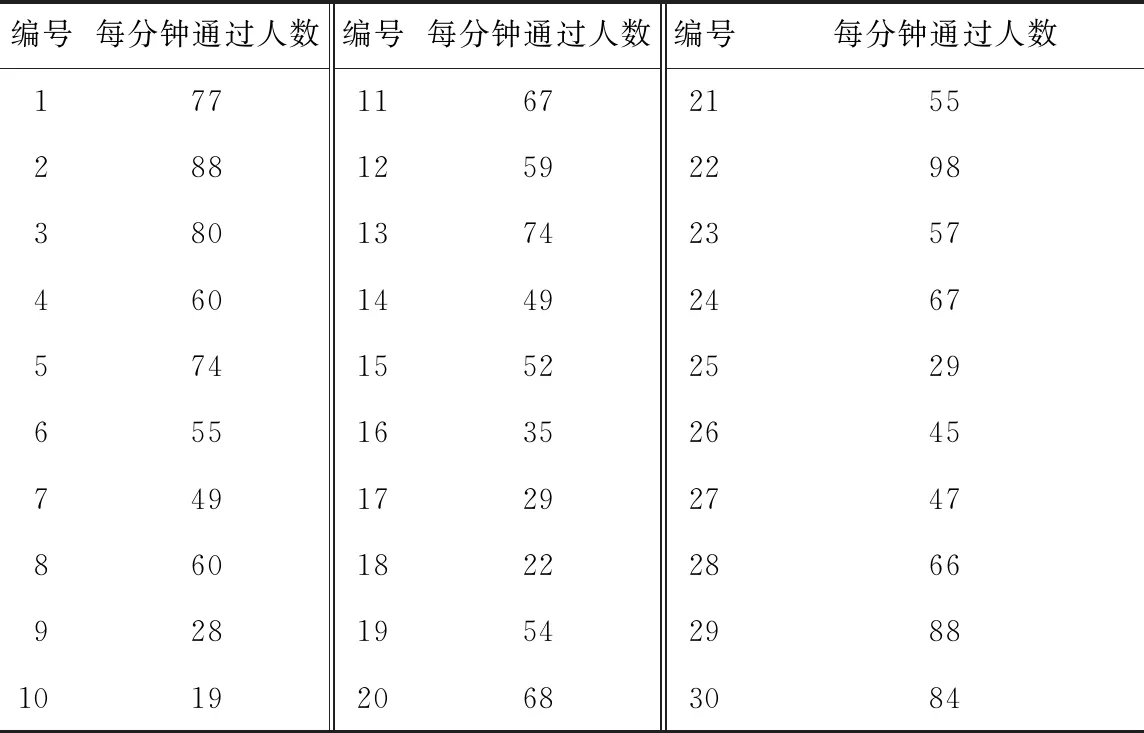
表3 每分钟各个地点通过人数

表4 每辆车行驶一圈搭载人数

从表4可看出，每辆车在行驶一圈所能装载的学生量为400人左右，根据此数据，15辆车行驶一圈的装载能力为6 000人左右。每辆车行驶一圈的时长大约是15 min，学生课间时间为30 min，在30 min内，15辆车能搭载的最大人数为12 000人，已知花江校区师生总人数为25 000人，在60%的乘坐意愿情况下，实验结果表明，这些公交能够满足大部分师生的出行需求。若公交开启双向通道运行模式，随着投入的车辆数增加，可以满足整个学校的乘车需求。

5 结束语

针对现有校园公交运营中的站点路线不固定和使用效率低的缺点，提出了一种理论化的研究方法，该方法通过使用0 -1整数规划确定站点的合理分配，使其满足大部分学生的需求，同时将公交线路转化为TSP问题，用蚁群算法进行求解，得到最优的校园公交行驶路线。最后，对校园公交的运载能力进行实验仿真模拟。本方法为校园公交系统的站台选址、线路优化等提供了一种理论参考，同时可推广至各个领域的相关问题。由于此方法仅考虑了公交线只有一条的情况，对于中小型的校园有很好的适用性，对于大型企业、科技园等来说需要拟定多条线路，后续还需做进一步改进。