“浅浅”教 深深学——罗鸣亮老师《分数与除法》教学赏析

文|邹瑞荣

一、深知学情，真疑导课

【课堂回放】

课始，罗老师以轻松语气说：“我们先来做几道除法吧！”他缓缓地依次读出如下除法算式，学生进行口算。

在学生逐渐困惑、迷茫的眼神中，罗老轻轻地问：“怎么了？遇到了什么困难？”

“除不尽了”“被除数比除数小，没法除”“除不了”……学生纷纷说出自己的真实困惑，罗老师随后板书：2÷3=？并问：“像这样的除法算式，商又该怎么表示呢？把你的想法在《学习单》上写一写。”

【赏析：学生在除法计算过程中遇到了困难，教师鼓励学生运用已有的知识经验尝试解决问题，学生自主想到用小数或者分数做商的办法，水到渠成地打通分数与除法之间的关系。当个别学生说出“”，分数和除法成功对接，可以找到它们之间的联系了。但罗老师此时并没有进行所谓的“点题”，而是轻轻一问“有道理吗”，让学生再次独立思考，深入探究2÷3 背后的道理。说理课堂要的不仅仅是一个除法计算的结果和眼睛看得到的分数与除法的简单关系，说理课堂还需要寻找这种关系背后的道理，寻找每一个计算结果背后的道理。】

二、深挖算理，多元构建

【课堂回放】

学生独立思考、小组交流后，汇报如下：

生1：（出示下图）把2 个饼平均分给A、B、C 三个人，第1 个饼每人可以分个，第2 个饼每人也可以分个，合起来每人就是分得个。

生2：把2 个蛋糕平均分成3份，（把两个圆各平均分成3 份）每人可以分2 份，凑起来就是个蛋糕。

学生再次独立思考，然后四人小组交流，再进行汇报：

学生出示下图，并进行讲解：3÷8 可以想成3 个1 分别除以8，1 个1 除以8 就等于，3 个合起来就是3 个，也就是。

师：11÷17 等于几？为什么？

师：不画图，想一想道理。

【赏析：罗老师一直循着“独立思考——四人小组交流——课堂对话”这样的路径“浅浅”地教着2÷3、3÷8 和11÷17，看似不变的教学流程其实无时无处不在悄然发生着变化。在变与不变之间，似乎又品出了一些说理课堂的味道。当基于学生困惑提出问题后，课堂一定要有充足时间让学生进行深入的独立思考。独立思考是开展四人小组交流讨论的前提，一方面能够确保每位学生都成为学习的主体，独立思考的环节为每一位学生的有效学习提供时间和空间上的保证；另一方面，独立思考与小组交流是课堂对话的预演，是高质量开展课堂对话的保证。在探究新知的关键处，课堂一直以这样稳定的状态推进着，学生在熟悉的学习环境中很清楚每一环节自己的任务，什么时候该思考，什么时候该表达，什么时候该倾听，学生心中都有数，他们学得很轻松。教师也就不用大费周章地进行组织教学，自然就可以“浅浅”地教。

在教学组织形式上不太多变的前提下，学生的学其实一直在发生着变化。从2÷3 大多数学生选择画图这种直观的表达方式说明算理；到3÷8 学生通过数的运算寻找计数单位，算清楚有几个说明算理；再到11÷17，罗老师让学生“不画图，想一想道理”，摆脱直观，进行抽象概括，纯粹从数的角度、从几个分数单位的角度深入理解11÷17 表示的是11 个，深度理解了分数与除法的关系。

在罗老师的课堂上学生可以主动地运用举例、画图、计算等多种形式理解、解释怎样用分数来表示除法计算的结果，以及这样表示的道理。学生不仅可以知道分数与除法有怎样的关系，更能清楚地知道它们是如何建立起这样的关系的。】

三、深度拓展，巧妙关联

【课堂回放】

在学生深刻理解2÷3、3÷8 和11÷17 这三个算式与分数之间的关系后，罗老师轻轻地问学生：能不能自己举个例子，考一考你的同桌？

生1：9÷19。

生2：999÷1011。

生3：5 个饼平均分给5 万5千个同学。

……

在好胜心驱使下，学生一门心思地想用更大的数考同桌时，罗老师话锋一转，笑着说道：“你们的水平都很一般。猜猜如果是我，我会考我同桌什么呢？”

停顿之后，缓缓地板书：4÷3=？

再次要求学生独立思考、小组交流，再汇报。

生1：4÷3=1……1，

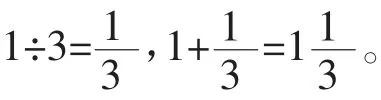
生2：（出示下图）把4 个饼平均分成3 分，每块饼每人分，4个饼每人就是分得。你们同意吗？

生3：4 个饼平均分 给3 个人，可以每人先分1 个饼，再把剩余的1 个饼平均分成3 份，每人再分个，合起来每人分到个饼。

【赏析：罗老师的课总会有峰回路转的精彩。当我还沉浸在欣赏学生举例的开放状态不能自拔的时候，罗老师话锋一转呈现出4÷3，巧妙地为学生再打开了一扇窗，让学生再次进入学习的新境界。在4÷3 的探索中，学生学习的触角自然而然地伸向了假分数、带分数的学习体验中，润物无声地沟通了“分数与除法”这节课与后续学习内容之间的关系，巧妙地打通了真分数、假分数、带分数之间的壁垒。从量的角度出发，深刻理解真分数、假分数、带分数的来龙去脉。这样四两拨千斤的“浅浅”教的背后是对单元知识结构深刻的理解和精准的把握，是对知识之间的关联的清晰判断。】