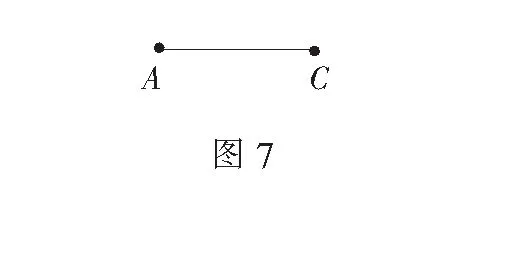
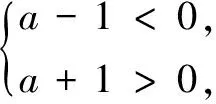探理思法 巧妙解题

田传弟

(江苏省徐州市铜山区三堡中学,221112)

问题是数学的心脏,解决问题是数学的特点.在解题教学中,只有引导学生阅读审题,分析题意,理顺条件,关联知识,探究出题目蕴含的数学原理,思考优化解题策略,才能有效迅捷地解决问题.下面我们举例说明,供大家参考.

例1北京冬奥会跳台滑雪项目比赛的标准台高度是90m.运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=ax2+bx+c(a≠0).图1记录了某运动员起跳后的x与y的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为( )

(A)10m (B)15m

(C)20m (D)22m

一般解法由题意,知抛物线y=ax2+bx+c(a≠0)经过点(0,90),可得c=90.

再把(40,82.2),(20,93.9)代入y=ax2+bx+90(a≠0),得

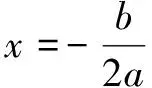
例2如图2,Rt∆ABC中,∠ACB=90°，AC=BC=4,D是AB边上的一个动点,以DC为斜边作Rt∆CDE,使∠CDE=30°，点E,A在CD的两侧,当点D从点A运动到点B时,点E的运动路程为______.

评析求“动点E的运动路程”的关键是弄清“动点E的运动路径(轨迹)”.而在初中阶段,可求长度的“动点的运动路径(轨迹)”只可能是线段或圆(或圆弧),二者必居其一.

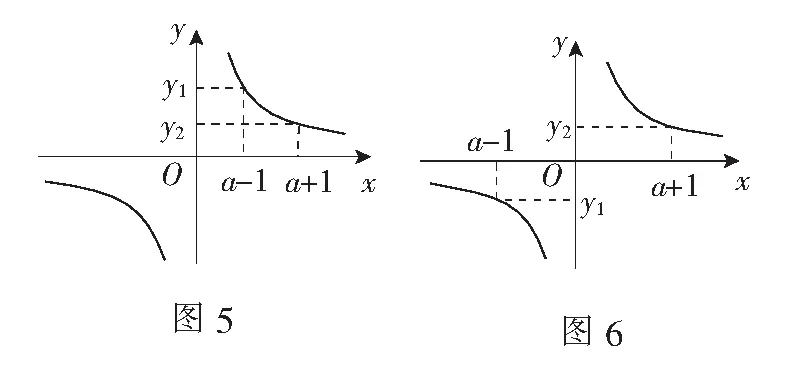
解因为a-1

①A,B都在原点左侧,如图4,可以看出y2

②A,B都在原点右侧,如图5,可以看出y2

综上所述,a的取值范围是-1

例4如图7,已知线段AC,用无刻度的直尺和圆规作Rt∆ABC,使得∠ACB=90°,∠BAC=60°.(不写作法,保留作图痕迹)

评析学生对此作图题往往无从下手,这可能是我们在平时教学中不够重视作图题的缘故.2022年版的数学课程标准对尺规作图提出了更高要求,所以加强尺规作图教学势在必行.这道作图题有多种方法,考虑到作∠BAC=60°,所以要先作出一个等边三角形,这是解决本题的关键所在.

解这里给出两种作图方法:如图8和如图9(作法略).

例5如图10,在正八边形ABCDEFGH中,四边形BCFG的面积为20cm2,则正八边形的面积为______cm2.

评析这是一种常规解法,但解答过程略显复杂.如果我们能充分发掘正八边形自身的一些性质,如中心对称性、轴对称性、旋转性质等,问题可得到秒解.

简解1如图12,连结AD,HE,分别交BG,CF于点M，N，P，Q，连结MP,NQ交于中心O,则矩形ADEH可以看作是矩形BCFG绕中心O旋转90°得到的,且两个矩形的重叠部分是正方形MNPQ.因为正方形MNPQ的边长与正八边形边长相等,所以等腰直角∆ABM,∆CDQ,∆EFP,∆GHN,∆MON,∆NOP,∆POQ和∆QOM都是全等的,由此可得S正八边形ABCDEFGH=2S矩形BCFG=40.故答案为40cm2.

我们在进行解题通法教学的同时,如果能够不失时机地引导学生探究问题的数学原理,思考知识的特性,充分发现和运用数学对象的内部关系,那么就有可能简化解题过程,从而提高学生的数学解题能力.