一题一课一世界——一道旋转题的多思、多解、多变

张 希 林 玲

(四川省成都市教科院附属学校,610000)

旋转是初等几何中的三大基本变换之一，也是初中数学中的一个难点.在每年的各类试题中,旋转问题常常作为压轴题出现.2020年成都市锦江区期末数学试卷第20题就是一道旋转题,它融合全等三角形、平面直角坐标系、三角形中位线、直角三角形等元素.本文对该题从不同视角展开解法探究并进行变式拓展,以期让学生体验数学问题的多彩性,以及对题型研究提供方向和指导.

一、试题呈现

(1)求证:AG=GF;

(2)略.

二、多彩解法

思路1以E为顶点构造手拉手模型

解法1如图2,过点E作EM⊥CB交CD与点M,连结MF,则得等腰Rt∆CEM，∴CE=ME.

由ED=EF,∠DEF=90°,易证∆CED≌∆MEF,∴MF=CD=AD,∠EMF=∠DCE=∠CME=45°,

∴∠CMF=90°=∠GDA,

∴∆MGF≌∆DGA,∴AG=GF.

思路2建系法+“一线三直角”模型

解法2如图3,以C为原点,CB所在直线为x轴,CA所在直线为y轴建立平面直角坐标系.过点E作ME⊥BC,过点D作DM⊥ME于点M,过点F作FN⊥ME于点N,则由“一线三直角”模型,可得∆DME≌∆ENF,

∴DM=EN,EM=NF.

设AC=BC=2a,CE=b,则A(0,2a),B(2a,0),D(a,a),E(b,0).

∴M(b,a),F(a+b,-a+b).

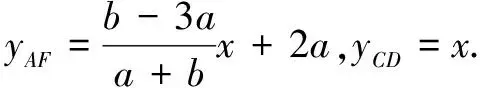
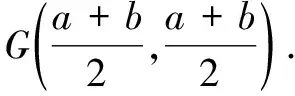
思路3构造“一线三直角”模型

解法3如图4,过点D作DM⊥BC于点M,过点F作FN⊥BC于点F，连结BF.

由“一线三直角”模型,可得∆DEM≌∆EFN,∴DM=EN,EM=FN.

易知∆DMB是等腰直角三角形,

∴BM=DM=EN，∴BN=EM=FN，

∴∆BNF是等腰直角三角形,

∴∠DBF=45°+45°=90°.

∵CD⊥AB,∴DG∥BF.

易知D是AB的中点,

∴G是AF的中点,即AG=GF.

思路4中位线法

如图5,过点E作EM⊥EB交AB于点M,连结BF,则得等腰Rt∆BEM.

∵DE⊥EF且DE=EF,

∴∆MDE≌∆BFE,

∴∠EMD=∠EBF=45°,

∴∠DBF=90°.

∵D是AB的中点,DG∥BF，

∴G是AF的中点,即AG=GF.

三、变式探究

爱因斯坦曾经说:“提出一个问题往往比解决一个问题更重要.因为解决问题也许仅是一个数学上或实验上的技能而已,而提出新的问题,却需要有创造性的想象力,而且标志着科学的真正进步.” “变式探究”是在“变式教学”的基础上,根据学生的特点,通过创设合理的、有挑战性的问题变式,激发学生的探究兴趣,点燃学生探究的种子.“变式探究”为学生的思维发展提供支架,同时有目的、有意识地引导学生从“变”的现象中发现“不变”的本质,从“不变”的本质中探究“变”的规律,真正做到融会贯通.

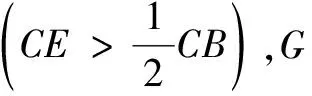
分析如图6,过点E作EM⊥EB交CG延长线于点M,连结MF.易证∆CDE≌∆MFE,

∴∠DCE=∠EMF=45°,CD=MF,

∴∠GMF=90°.

又∵CD是等腰Rt∆ACB斜边中线，

∴MF=CD=AD，

∴∆AGD≌∆FGM,∴AG=GF.

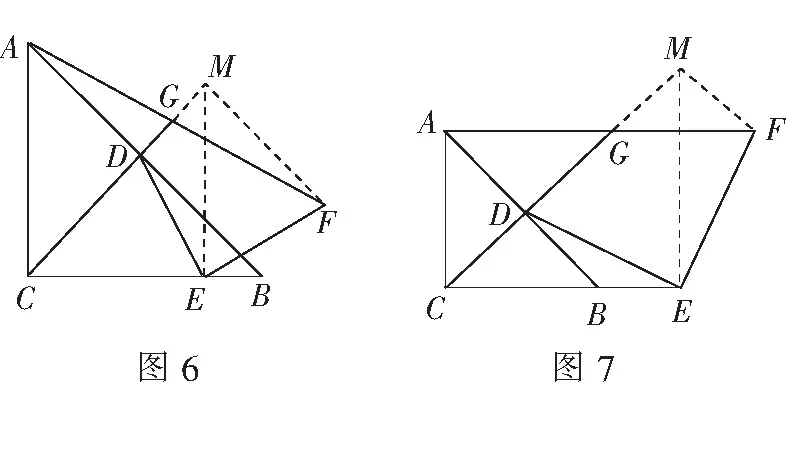
变式2点E是线段CB延长线上一点,G是AF与CD延长线的交点,问AG与GF是否相等?

分析如图7,过点E作EM⊥EB交CG延长线于点M,连结MF.易证∆CDE≌∆MFE,

∴∠DCE=∠EMF=45°,CD=MF,

∴∠CMF=90°.

同理，可证∆AGD≌∆FGM,∴AG=GF.

变式3点E是线段BC延长线上一点,问AG与GF是否相等?

分析如图8,过点F作FM⊥DG的延长线于点M,过点D作DN⊥BE于点N,过点F作FL⊥EN于点L，连结BF.

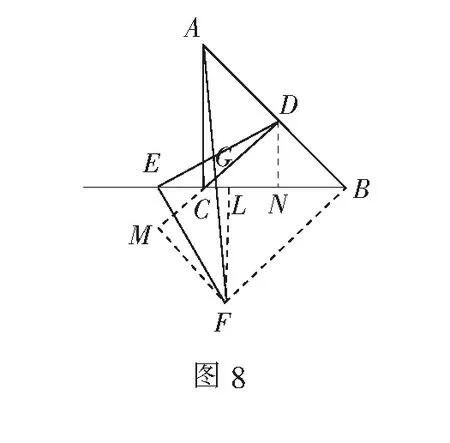
由“一线三垂直”模型,可得∆DEN≌∆EFL,∴EN=FL,EL=DN.

∵∆DNB是等腰直角三角形,

∴DN=NB,∴BL=FL,

∴∆BLF是等腰直角三角形,

∴∠DBF=90°.

易得长方形BDEF，∴MF=BD=AD，

∴∆AGD≌∆FGM,∴AG=GF.

变式4当点E在直线BC上运动时,求点C到直线BF的最小值.

分析点E是主动点,点F是从动点,当点E在直线BC上运动时,点F的运动轨迹也是一条直线.这也是我们常说的“瓜豆原理”.

如图8,当点E是BC的中点N时,点F与点B重合.

由解法2,可知kBF=1,所以点F的轨迹是过点B且平行于CD的直线.

∵CD⊥AB,

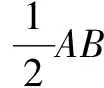
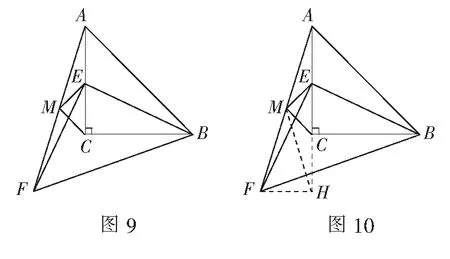
变式5如图9,在Rt∆ABC中,∠ACB=90°,AC=BC,点E在AC上运动,连结BE,把BE绕点E顺时针旋转90°到点F,连结AF.取AF的中点M,连结ME,MC,求证:ME=MC.

证明如图10,过点F作FH⊥EC的延长线于点H,连结MH.

易证∆ECB≌∆FHE,

∴FH=CE,CH=AE.

在Rt∆AHF中，MH为斜边中线,

∴AM=MH，∠MAE=∠MHC，

∴∆AEM≌∆HCM,∴ME=MC.

四、结束语

本着以观察为起点,以问题为主线,以培养能力为核心的宗旨,笔者着意培养学生观察、分析、抽象、概括的能力,引导学生从运动、变化的角度看问题,这不仅叩开学生思维之门,也打开了他们的心灵之窗.

本题是旋转类几何综合题,学生经历了探索图形旋转过程,已经积累了相当的图形变换的数学活动经验,他们的逻辑思维从经验型逐步向理论型发展,观察能力、记忆能力和想象能力也得到了迅速的提升.

本文从一题多解,到一题多变,整节课环环相扣,节奏紧凑,有助于提高学生的学习效率,提升学生的思维品质.