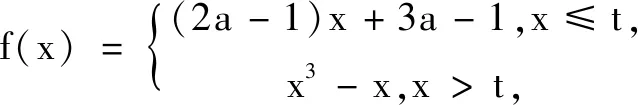着力解题反思 培养良好习惯

孙 晶

(江苏省南京市建邺高级中学 ，210000)

解题后的反思是完整解题的重要环节,是具有完备应答能力的重要体现,也反映一个应试者的数学素养.通过反思,能及时发现解题过程中的错误和遗漏,完善解题目标,优化思维品质．所谓的解题后反思,是指解决数学问题之后,通过对解题计划、解题途径、解题过程、解题实质的回顾,进一步暴露解题的思维过程,检查整个解题的准确性、合理性和完备性,让优秀的解题经验发扬光大,避免同样的错误再一次的发生，为养成良好的解题习惯、发展思维能力、培养学生的数学素养提供一个重要平台．那么如何进行解题后的反思呢?

一、回顾题意

再一次审题，就是一种重要的解题后反思.题目解答完后,回头将题目的重点再重温一遍,看清所给式子的结构特点和待求结论具体要求,以及括号内的注解等,这样就可能降低解题错误的发生率,使解题过程趋于完整、规范．

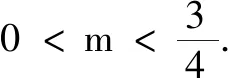
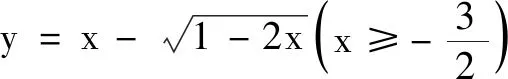
二、挖掘隐含

许多条件可能隐含在一些表面文字的背后,或者隐含在解题过程中的某个式子中,需要通过对整个解题思路和解题过程的反思,才能清晰地意识到条件的存在.如果能够得到充分理解和及时使用,就能使解题更加优化和完美．

例3已知3x2+2y2=9x,求x2+y2的最值．

第一类：“脱离家庭环境的儿童”。指暂时或永久性脱离家庭环境的儿童，或为其最大利益不能在家庭环境下继续生活的儿童。这包括被遗弃儿童，被拐卖儿童，孤儿，父母被剥夺监护权的儿童和流浪儿童。

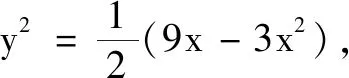
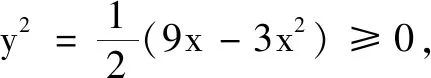
例4二次函数f(x)=ax2+bx+1(a>0,b∈R),设方程f(x)=x有两个实根x1,x2,如果x1<2-1．

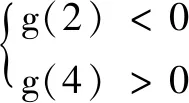
三、研究多解

一道题解完后,如果能对其进行进一步的探讨,或者说换一种思路、换一个角度思考,有可能发现新的解题方法.这样可以使思维变得活跃,目光变得开阔,对提升思维品质有很大作用．

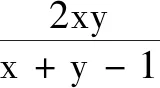
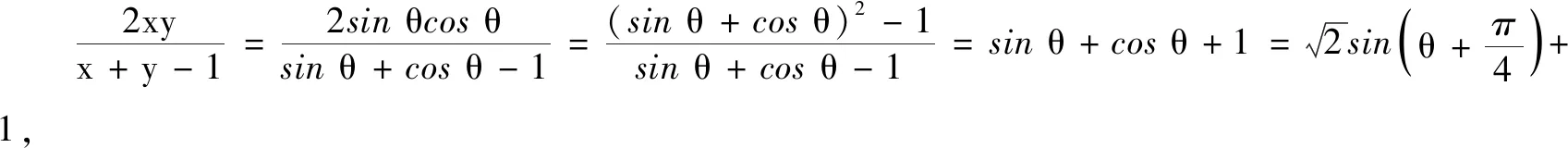
反思此解法有没有错误呢?分式的分母有没有考虑呢?事实上,由sinθ+cosθ-1≠0,可知sinθ+cosθ+1≠2,故取值范围中应该去掉y=2．

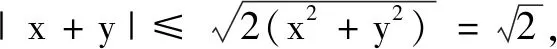
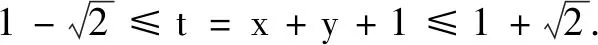
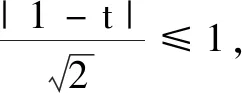
当然还有多种解法,只要多注意反思,就可能够将不熟悉的问题转化为熟悉且经典的问题．

四、探索规律

通过反思一道题的求解过程,然后类比与之相近的题目,探究它们解法的可比性,从中发现一些解题规律,并进行推而广之,达到会做一道题,就能会做一类题的目的．这样既可及时归纳解题方法,形成解题经验,也强化知识点之间的联系,集约化、模块化知识体系,使数学学习过程变得轻松愉悦．

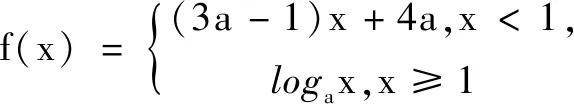
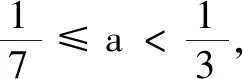
通过反思求解过程可知,此题就是抓住函数单调性定义求解的．再看类似的三个题目．

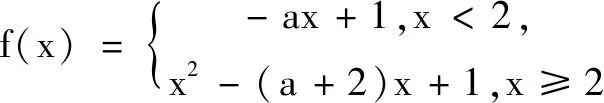
此题与上述问题非常相像,属于同类问题.因为分段函数是增函数,需要充分理解增函数定义,即对于任意x1

本题虽然没有函数单调性的表述,在分析题意后可知问题就是要求函数f(x)不能是单调函数.同样可以用判断函数单调性进行分析,建立相关不等式解题.事实上，由于f(x)是一个分段函数,且当x≥1时,是一个开口向下的二次函数,对称轴为x=a；当x<1时,是一次函数.若a>1,则抛物线的对称轴在x=1右边,且2a>0,此时一次函数单调增,满足f(x)不能单调函数;当0≤a≤1时,抛物线的对称轴在x=1左边,且2a>0,此时一次函数单调增,也满足f(x)不能单调函数;当a<0时,抛物线的对称轴在x=1左边,且2a<0,此时一次函数单调减,则f(x)单调减函数,不合题意,故而实数a的取值范围是[0,+∞)．

显然后面的三道题与原题虽然表面叙述不同,但采用的解题思路都是利用函数的单调性去解决,这就是此类问题的求解规律,即抓住单调性是解题核心．

解题后的反思有多种形式,根据不同问题、不同需求,可以有不同的选择,其实就是要培养一种良好的解题习惯,让解题过程少走弯路,让学习过程心情愉悦,让应试过程信心满满．