巧用数形转化 突破解题瓶颈——两道数学试题解法的探究与思考

邵海贤

(扬州大学数学科学学院，225000)

数形转化是指借助几何图形的直观性与代数的量化性，将数量关系问题转化为图形的性质问题解决，或者把图形的性质问题转化为数量关系的问题研究[1].它主要包括几何问题代数化与代数问题几何化两个方面.“以形助数,以数解形”，可以化抽象为具体,化复杂为简单，变抽象思维为形象思维.但是实现数与形的合理转化并非易事，如何根据题意分析转化条件、探究转化方向、设计转化路径、确定转化程序？如何合理作图、有效识图以及遇到难题时如何调整运算与转化思路？这些都是学生的难点与弱点.因此应引导学生以用数学的眼光观察题目特征为先导，用数学的思维为解法寻找辩护的“理由”，让解法在师生的交流中“自然分娩”[2].这是教师应重视的问题.

一、以数助形 几何关系数量化

以数助形，将图形中的几何要素与几何关系用代数的语言进行描述，实现几何问题代数化，再通过观察代数结果的几何意义，进而解决问题.此类思路的关键在于学生能否巧妙地从形中挖掘出隐藏的数量关系，将图形语言转化为代数语言.

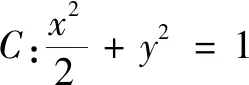
(1)当l与x轴垂直时，求直线AM的方程;

(2)设O为坐标原点证明:∠OMA=∠OMB.

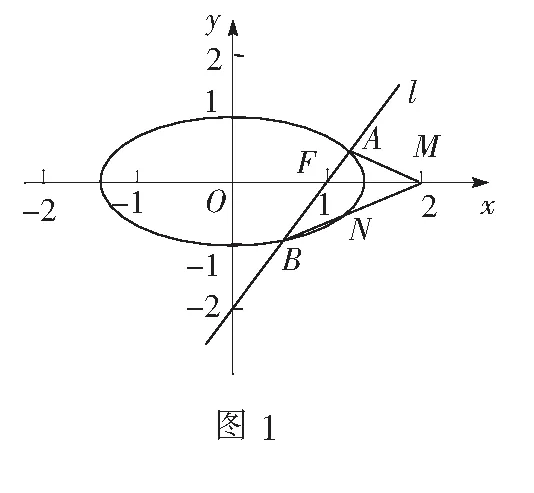
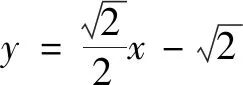
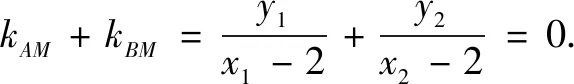
评析思路1是把两角相等的几何问题转化为两直线斜率之和为零的代数问题.思路1主要是设点坐标与直线方程，构造直线斜率、求和，将直线方程代入椭圆方程，再利用韦达定理计算化简求得结果，体现了解析的思想.整个运算过程计算量适中，但需注意对于直线方程斜率是否存在的情况，需要进行分类讨论.

思路2设直线MB的方程y=k1(x-2)(k1≠0).若证得点A关于x轴的对称点N在直线MB上,再由椭圆的对称性即可得出∠OMA=∠OMB.假设点N在直线MB上，则y2=k1(x2-2)，-y1=k1(x1-2),如果证出y2(x1-2)+y1(x2-2)=0，就可说明假设成立.将y1=k(x1-1)与y2=k(x2-1)代入上式，再将直线l与椭圆方程联立得出韦达定理公式代入，只需证2kx1x2-3k(x1+x2)+4k=0，由上述论证可知等式成立.

评析思路2主要是通过假设猜想结论，再利用推理验证其猜想的正确性.这种思路相对于思路1而言，学生接触较少，但是体现了解题思路的创造性.数形转化思想在高考题中应用较为广泛，这就要求注重培养学生的数形转化思想意识，以开拓学生的思维视野.

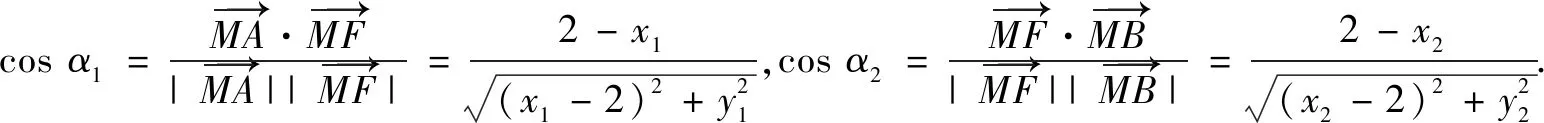
评析向量是沟通几何与代数关系的桥梁，它将数形融为一体.此解法利用向量数量积的定义求夹角，思路清晰明确.建立合适的坐标系在向量法中可起到事半功倍的效果.思路3借助向量求解比前两种解法计算量更大，但简化了学生思考的过程，提供了新的思考方向.

二、以形助数 数量关系直观化

以形助数，借助通俗易懂的直观图形解决抽象的代数问题，从而使复杂的数学问题具体化、直观化.它能够让学生在生动形象的几何图形中理解量的关系，有助于学生直观想象、数学抽象等核心素养的发展.

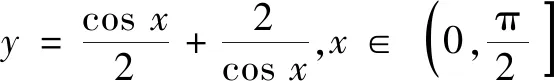
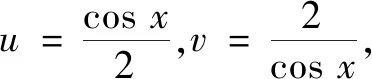
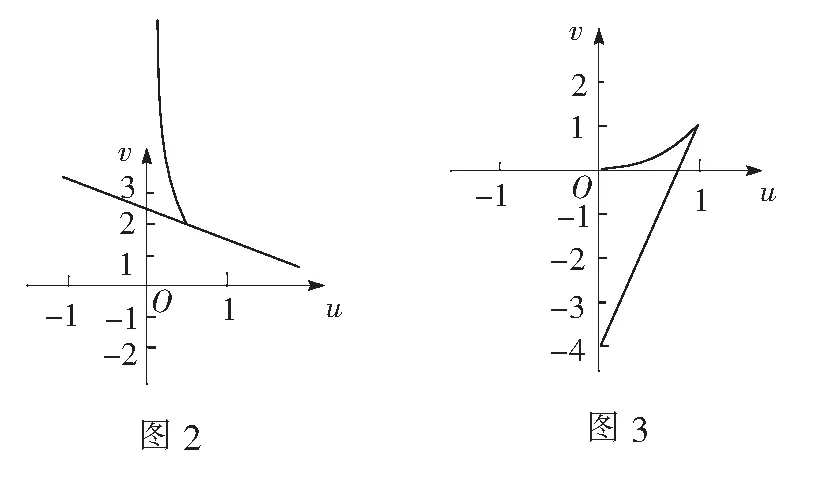
评析本题若通过求导、判断函数图象单调性直接求解比较复杂，不妨以形助数，从图象的角度分析，赋予函数一定的几何意义，进而将问题几何化、简洁化.由函数代数式的特性可联想到解析几何中的曲线方程，从而利用曲线的几何特征的直观性解决问题.

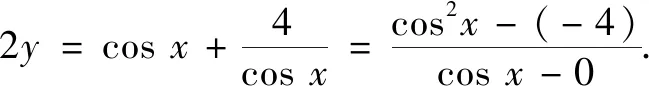
评析思路1与思路2都是通过对变量进行构造或整体代换，把求函数最小值的代数问题转化为求最小截距与最小斜率的几何问题.在整个解题过程中，将抽象的函数最值问题转化为直观的几何问题，体现代数问题几何化的转化思想，这不仅可简化问题，还有利于学生解题综合能力的提高.

数形转化为几何问题代数化与代数问题几何化提供了良好的载体，它能够变问题简单化、明朗化.新课标指出，通过高中阶段的学习，学生能够掌握“四基”,发展“四能”，从而培养学生的数学核心素养.因此，作为新时代的教师，要在具体的课堂实践中，以核心素养为生长点，落实课堂目标，优化课堂启发方式，深化解法对比探究，引导学生找到数形转化中的切入点，提升学生的逻辑思维能力，为学生以后的数学生涯奠定坚实有力的基础.