基于Norton幂律方程的再生器筒体蠕变性能分析及仿真

郭金泉，刘海林，张经伟，刘康林，黄齐飞，郭帅

(1.福州大学机械工程及自动化学院, 福建 福州 350108；2.福建省力值计量测试重点实验室(福建省计量科学研究院), 福建 福州 350003；3.福州大学石油化工学院, 福建 福州 350108; 4.福建省特种设备检验研究院, 福建 福州 350028)

0 引言

某厂一台在役催化裂化再生器，筒体材料为Q245R钢，其内部介质工作最高温度达720 ℃.由于服役环境的恶劣性，其内衬发生破损，导致局部区域筒体与高温介质直接接触.而Q245R钢不适宜长时间在高温环境下使用，且目前也无相关文献报道该材料在高温下的蠕变性能，所以为保证该设备的安全服役，需对筒体材料进行高温蠕变行为研究.材料蠕变是高温构件最常见的失效方式[1-3]，如长期受到高温蠕变的影响，重油催化劣化装置出现筒体鼓包、 锅炉压力容器烟管变形及反应堆压力容器封头断裂[4]等情形.这些在恶劣环境下服役的设备，一旦发生事故，即会对生命财产安全构成威胁，所以对再生器筒体蠕变性能进行分析和研究，对设备的安全生产和人身安全有着重大的意义.

高温下金属的蠕变性能是衡量金属材料强度的一个重要指标，其常用的研究手段是单轴蠕变试验并建立蠕变本构模型进行描述[5-6].目前已有大量学者提出不同的单轴蠕变本构关系，而其中较为常用的有Norton幂律方程及Norton-Bailey本构方程，它们被广泛应用于描述大部分的金属材料的本构关系[7].徐鸿等[8]基于Norton-Bailey模型对P92钢进行了蠕变分析，并结合Norton方程，得到能够同时描述蠕变第一及第二阶段的蠕变方程.BRANDO等[9]基于Norton幂律方程对航空用材7050铝合金进行蠕变时效成形研究与有限元计算，结果表明基于Norton幂律的简化模型可有效地应用于7050铝合金的蠕变时效研究中.Zhao等[10]提出一种锆合金高温氧化的相场模型，并利用理想弹塑性模型和Norton幂律蠕变方程预测锆合金弹塑性形变和使用一维氧化情况验证相场模型结果，表明其与实验结果吻合较好.本研究对再生器筒体材料Q245R钢在其现场监测到壁温550 ℃时，对不同应力水平进行单轴蠕变试验，建立550 ℃下该材料的Norton幂律方程，并将得到的蠕变本构方程代入ABAQUS中对再生器出现鼓包的局部区域进行有限元分析，为安全评定提供依据.

1 筒体参数及试验方法

再生器筒体在实际服役工况下其所受到的内压p为0.24 MPa，筒体壁厚δ1为24 mm，内径Di为5 800 mm； 在鼓包区域附近有一接管，壁厚δ2为12 mm，内径di为1 400 mm.根据其实际的服役工况，可以得到筒体的环向薄膜应力σθ为：

(1)

筒体的轴向薄膜应力σm1为：

(2)

接管所受到的轴向薄膜应力σm2为：

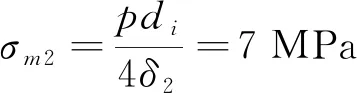
(3)

蠕变试验试样根据《金属材料 单轴拉伸试验蠕变方法(GB/T 2039—2012)》[11]加工成标距为50 mm，直径为10 mm的试样，具体试样尺寸如图1所示.因为在国标与已有的文献中，只能查到Q245R钢最高450 ℃时的力学性能参数，所以需要对该材料进行高温力学性能研究，其拉伸试样与单轴蠕变试样相同，高温拉伸试验温度为550和600 ℃，根据《金属材料拉伸试验： 高温试验方法(GB/T 228.2—2015)》[12]安装好试样后，保温30 min后开始高温拉伸试验，预载荷为200 N.蠕变试验采用CTM-105B1高温蠕变试验机，试验过程中保持载荷不变，试验为位移加载，加载速率为0.2 mm·min-1，温度为上中下三点控温，温度误差为±1℃.试验条件为550 ℃下，加载载荷分别取筒体环向薄膜应力σθ的1.50、 2.25、 2.50、 2.75和3.00倍，即43.50、 65.25、 72.50、 79.75和87.00 MPa.

2 试验结果及分析

2.1 高温拉伸试验结果

对Q245R钢材料在550和600 ℃下进行高温单轴拉伸试验，得到的高温拉伸曲线如图2所示.表1给出Q245R钢不同温度下的基本力学性能参数，其中常温和450 ℃时的力学性能为《锅炉和压力容器用钢(GB/T 713—2014)》[13]的数据.表1中：σb为抗拉强度；σs(σ0.2)为屈服极限；δ为延伸率.

表1 Q245R钢高温拉伸试验结果

由表1可知，常温下与高温下该材料的力学性能差别较大，说明其高温力学性能较差； Q245R钢随着温度的增加，其抗拉强度、 屈服极限和弹性模量都呈明显降低； 且高温下的延伸率是常温下的2倍，说明高温软化了材料，导致延伸率增加.

2.2 高温单轴蠕变试验结果

根据CTM-105B1高温蠕变试验机中的试验数据，得到Q245R钢时间-应变曲线，如图3所示.表2为单轴蠕变试验得到的最小蠕变率.从图3可看出，在550 ℃下Q245R钢的蠕变第一阶段并不明显.而由表2可看出，550 ℃下Q245R钢随着应力的增加，其最小蠕变速率增大，表明随着应力的增加，Q245R钢的抗蠕变性能降低.由于本文未进行不同温度、 相同应力的蠕变试验，所以Q245R钢随温度改变的时间-应变规律并未给出，但是由金属蠕变的大致规律可以得到在相同应力下，温度越大，蠕变速率越快，材料的抗蠕变性能越低[14].

表2 Q245R钢550 ℃单轴蠕变试验结果

3 本构方程与有限元分析

3.1 本构方程

在恒温恒载荷的情况下，金属的蠕变应变不仅与温度和应力相关，还与时间相关，所以蠕变应变εc可写成与时间t、 温度T和应力σ的函数关系式[15]：

εc=f1(σ)f2(t)f3(T)

(4)

一般应力水平与蠕变速率在双对数坐标系中呈现线性关系，下式为蠕变和应力的关系式； 而时间对于蠕变来说存在相关性，一般是由试验结果拟合得到； 受试验条件限制，本文只考虑550 ℃温度下材料的蠕变，因此不考虑不同温度的影响[16].

f1(σ)=Aσn

(5)

式中：A为与温度、 材料特性相关的常数；n为应力指数.

在恒应力下的蠕变试验结果表明，蠕变第二阶段的蠕变率为恒定值，可得到Norton幂律方程：

(6)

3.2 Q245R钢本构模型参数的确定

从图3的蠕变曲线可知，Q245R钢的蠕变第一阶段时间短，可以忽略不计.所以使用下式来描述Q245R钢的蠕变性能，对式(6)取对数得：

(7)

由图4可获得A2与n2的值，其中A2=9.41×10-17，n2=6.57.在常用的蠕变研究方法中，可通过应力指数n2来表征材料的蠕变变形机制[17-19].当n2=1时，金属材料的变形机制主要为扩散蠕变； 当n2=2时，金属材料的变形机制主要为位错滑移； 当n2=4～7内时，金属材料的变形机制主要为位错攀移； 当n2>7时，此时无法预测金属材料的蠕变机制.根据试验蠕变曲线数据得到n2的拟合值为6.57，其在4～7内，因此，Q245R钢在550 ℃下的蠕变机制主要以位错攀移为主.

3.3 有限元分析

根据再生器筒体接管鼓包区域实际情况，借助ABAQUS有限元软件，对再生器在550 ℃时的高温蠕变行为进行模拟研究.由于整个筒体为对称模型且此次内衬失效出现在筒体接管上方处，因此取该局部区域二分之一进行建模，有限元模型如图5所示.该模型采用C3D8R六面体单元划分，共划分102 136个单元，129 485个节点.在筒体内壁施加内压0.24 MPa，模型上端面施加筒体轴向等效应力σm1=14.5 MPa，接管端面上施加接管轴向等效应力σm2=7.0 MPa； 在模型下端施加Y向约束uY=0，在接管与筒体的对称面上施加对称性约束.

对该模型进行蠕变有限元计算，本构模型采用式(6)的Norton幂律模型，模拟结果如图6所示.由图6可知，最大Mises应力为65.3 MPa, 发生在筒体和接管相贯处附近区域，通过应力分析与评定，可知一次局部薄膜应力为54.3 MPa，一次+二次应力为64.8 MPa，其值均小于设计应力强度许用极限，说明该区域在不考虑高温引起材料劣化和温度梯度对筒体影响的情况下是满足强度要求的.从图6(b)中可以看出筒体受到内压和高温影响后，最大变形量为91.3 mm与现场筒体衬里破坏后筒体超温部分变形量90 mm相近，最大变形位置主要分布在筒体与接管相贯处上方600 mm处，该最大变形量位置与现场所测位置基本吻合，说明用该方法来预测再生器短期的蠕变行为是可行有效的.图6(c)为等效蠕变率的分布图，其分布趋势与Mises应力分布基本一致，说明应力的分布与材料的蠕变损伤及扩展有着密切的联系，这与文献[20]结论一致.

为确定Mises应力、 蠕变变形量及等效蠕变率的分布区域，本文以对称面上的筒体与接管相贯处为起点，分别沿筒体轴向和接管环向建立两条路径，如图6(d)所示，将相关力学量映射到路径上，得到结果如图7所示.从图7可看出，等效蠕变率与Mises应力沿筒体轴向和接管环向的曲线趋势基本一致； 从图7(a)知，等效蠕变率与Mises应力值随着远离相贯处呈先减小后保持不变或略微增大，蠕变变形量随着远离相贯处呈先增大后减小，最大蠕变变形发生在离筒体与接管相贯点600 mm处.由图7(b)可知，等效蠕变率与Mises应力在接管正下方和正上方处值最大，而蠕变变形则呈相反的趋势.因此，为保证再生器的安全服役，需在该区域进行定期监测和加固.

4 结语

1) 通过高温单轴拉伸试验可知，该材料的力学性能随着温度增加呈明显下降，并与常温差别较大； 由高温蠕变试验可知，该材料在550 ℃下的蠕变曲线第一阶段不明显，且随着应力的增大Q245R钢的蠕变速率明显增大，即材料的抗蠕变性能随应力增加而降低.

3) 由有限元仿真分析可知，最大蠕变变形量为91.3 mm，最大蠕变变形发生在接管相贯处上方600 mm处，与现场实测相近，说明本文建立的Q245R材料蠕变本构模型和有限元仿真计算是有效的，可为定期监测和加固提供依据.后续将继续完善蠕变试验，得到完整的蠕变曲线，并对该材料的蠕变规律进一步深入研究，为筒体的安全运行提供更加可靠的参考.