带边缘增强的反比相对距离加权均值滤波

邓 田

(南昌工学院 信息与人工智能学院，江西 南昌 330108)

0 引言

椒盐噪声的去除最初用中值滤波算法[1]，但是对于高密度噪声的去除，该方法的效果较差，而开关中值滤波[2-3]有针对性地对噪声像素进行处理。随后，自适应中值滤波[4-5]因其良好的自适应性和鲁棒性而被提出。一般地，邻域中像素之间的相关性，随空间距离的差异而不同。于是部分学者提出了加权中值和加权均值滤波算法[6-7]。噪声检测的准确性在一定程度上决定着最终的去噪效果。Erkan等[8]根据噪声密度设置上、下阈值以提升噪声检测的准确性。Samantaray等[9]采用一种邻域决策方法检测噪声。进一步地，文献[10]通过对邻域的决策性分析来检测噪声。

鉴于深度学习在图像处理中的广泛应用，部分学者提出了基于深度学习的图像去噪方法[11-14]。但是基于深度学习的图像去噪的良好性能往往以较高的计算耗时为代价[15]。为了降低算法的计算复杂度，Fareed等[16]提出了快速的均值滤波算法。Lee等[17]提出了改进像素的快速中值滤波算法，该算法具有较快的处理速度，但是其在去噪性能上并没有显著的优势。

为了进一步提升图像的去噪效果，提出了一种带边缘增强的反比相对距离的加权均值滤波方法。根据噪声的灰度特征和无噪像素的分布特征进行噪声检测，然后用反比于相对空间距离的加权均值滤波对噪声像素进行恢复，最后用拉普拉斯算子对去噪图像进行边缘增强，以得到边缘增强的去噪图像。实验结果显示，本文方法相对于部分现有方法取得更好的去噪效果，边缘和纹理结构恢复得更好。

1 基于无噪像素分布的噪声检测

椒盐噪声取图像灰度的最小值和最大值，对于8位灰度图像，椒盐噪声取灰度0和255。最小值噪声与最大值噪声等概率地随机分布于图像中。椒盐噪声的数学模型为：

(1)

式中，x为像素；P为概率函数；d为噪声的密度。值得注意的是，椒盐噪声取灰度最小值和最大值，但是图像中的部分无噪像素或许也取灰度最小值和最大值。因此，对椒盐噪声检测的关键是，将椒盐噪声与取灰度最小值和最大值的无噪像素区分开，避免无噪像素被后续的去噪处理破坏。因此，提出了基于椒盐噪声灰度特征以及无噪像素分布特征的噪声检测方法，具体步骤如下：

① 将图像中灰度取最小值和最大值的像素识别为可疑噪声像素，其余为无噪像素。

② 对于每一可疑噪声像素，如果其3×3邻域中的所有像素都取相同的灰度值(比如，可疑噪声像素的灰度取0，而其3×3邻域中的所有像素均为0)，将当前可疑噪声像素识别为无噪声像素。

③ 对于每一可疑噪声像素，如果有一条所有像素灰度相同的直线或曲线经过它，将该噪声像素识别为无噪像素。

④ 所有其余的可疑噪声识别为噪声像素。

步骤①的依据为如式(1)的噪声模型，噪声像素的灰度一定为最小值和最大值。步骤②的依据为当前像素处于黑色的区域(灰度取最小值)或白色的区域(灰度取最大值)上，当前可疑噪声本身就属于图像的区域信息，如图1(a)所示。步骤③的依据为当前像素处于一条黑色(灰度取最小值)或白色(灰度取最大值)的线条上，当前可疑噪声像素本身就属于图像的边缘信息，如图1(b)～图1(d)所示。图1所示仅为最小值无噪像素的情况，最大值无噪像素的情况与此相同。

(a) 黑色区域

2 反比相对距离的自适应像素恢复

一般地，开关中值滤波和开关均值滤波分别用邻域中无噪像素的中值或均值对噪声像素进行代替，其从统计意义对噪声像素进行恢复。但是邻域中各像素因相对于中心噪声像素的距离不同，其对噪声像素的影响和相关性也不同，因此开关中值滤波和开关均值滤波对噪声像素的恢复估测往往偏差较大。为了更准确地体现邻域中无噪像素对中心像素的影响和相关性，提出了反比于相对空间距离的自适应加权均值滤波方法。各尺度邻域的加权算子如图2所示，更大尺度的加权算子类似地定义。

(a) 尺度3×3的加权算子

对每一噪声像素，优先用小的去噪邻域中的无噪像素进行恢复，只有当小邻域中没有无噪像素可利用时，才逐步扩大去噪邻域，直到当前邻域存在可用的无噪像素或邻域的尺度超过预设值。因此，对于每一个尺度的邻域，可用的无噪像素只可能存在于邻域的边沿上，如图2所示，所以对每一尺度的加权算子，其除边沿像素外的所有内部像素对应的加权系数均为0。另外，邻域边沿上的加权系数是对应于无噪像素的加权系数，如果边沿上的像素为噪声，则其加权系数为0。

加权算子的各个加权系数严格反比于其与中心位置的相对距离。对每一尺度的邻域，水平和垂直方向位置的像素与中心位置的距离最近，设置系数为1，其余位置的加权系数严格反比于其相对于中心位置的距离与水平或垂直方向位置相对于中心位置的距离的比值。

3 去噪图像的边缘增强

由于噪声的破坏以及去噪处理的偏差，图像的纹理结构和边缘细节会受到一定程度的破坏，虽然可以在图像去噪处理中得到一定程度的恢复，但是去噪处理后的纹理结构和边缘细节较弱，因此一般的去噪图像会有不同程度的模糊。因此，本文对去噪图像做后边缘增强处理，以恢复图像的纹理结构和边缘细节。

对图像进行边缘提取，与一阶微分相比，二阶微分的边缘定位能力更强，锐化效果更好。作为二阶微分算子的拉普拉斯算子是各向同性微分算子，具有旋转不变性。因此，本文采用拉普拉斯算子对去噪图像做后边缘增强处理。拉普拉斯算子分为中心系数为正和中心系数为负2种，如图3所示。

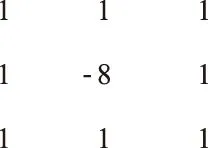
(a) 中心系数为负

从拉普拉斯算子可以看出，如果在图像中一个较暗的区域出现了一个亮点，那么用拉普拉斯算子就会使这个亮点变得更亮。因为图像中的纹理结构和边缘细节就是那些灰度发生跳变的区域，所以拉普拉斯算子在边缘检测中很有效。拉普拉斯算子既可以有效增强纹理结构和边缘细节，同时又能保留背景信息。

将经反比相对距离加权均值滤波去噪处理的图像，用拉普拉斯算子进行纹理结构和边缘提取，然后线性叠加到去噪图像中，使得被噪声和去噪处理破坏的纹理结构和边缘细节得到一定程度的恢复。这样可以使去噪图像的各灰度值得到保留，同时使灰度突变处的对比度得到增强，最终结果是在保留图像背景的前提下，突出图像的纹理结构和边缘细节。

4 实验验证分析

实验平台的硬件为i5 CPU和8 GB RAM的计算机，软件为Windows7操作系统和Matlab 2019a。以结构相似性(Structural Similarity，SSIM)指数和边缘保持指数(Edge Preserve Index,EPI)[18]、视觉感知以及执行效率作为指标，将本文提出的方法与文献[7,9,15-16]中提出的方法应用于图像去噪实验，并对实验结果进行分析与比较，以验证本文方法在去噪效果、边缘恢复以及执行效率上的综合性能。去噪图像采用图像处理领域的数据集Set12和BSD68中的部分图像，如图4所示。在实验中，将实验图像添加从低到高不同密度的噪声，以验证方法应对不同密度噪声的鲁棒性。

(a) man

4.1 去噪的SSIM和EPI

本文方法有别于一般去噪方法的一个特色就是图像去噪后的边缘增强处理。为了在验证本文方法去噪性能的同时，验证边缘增强所起的作用，本小节中将不带边缘增强的去噪方法称为本文方法1，而带边缘增强的去噪方法称为本文方法2。

以曲线形式将各算法对图像man去噪结果的SSIM和EPI如图5所示。对于SSIM，在噪声密度较低时，各算法的差距较小，但是明显可以看出，本文方法2的SSIM值稍微高于其他算法；随着噪声密度的增大，各算法在去噪效果上的差距逐步拉大。在噪声密度较高时，文献[7,9]方法的SSIM值较低，其次是文献[16]。文献[15]和本文方法1相差不大，但在噪声密度较高时，本文方法1还是稍微高于文献[15]。相对地，本文方法2的SSIM值一致高于其他算法。对于EPI，EPI曲线的走向比较集中，各算法的差距较小，但是总体上本文方法1和本文方法2稍微高于其他算法，本文方法2的EPI值最大。因此，本文方法相对于现有的算法，具有更好的去噪性能，在去除噪声的同时能较好地保持和恢复图像的纹理结构和边缘细节。

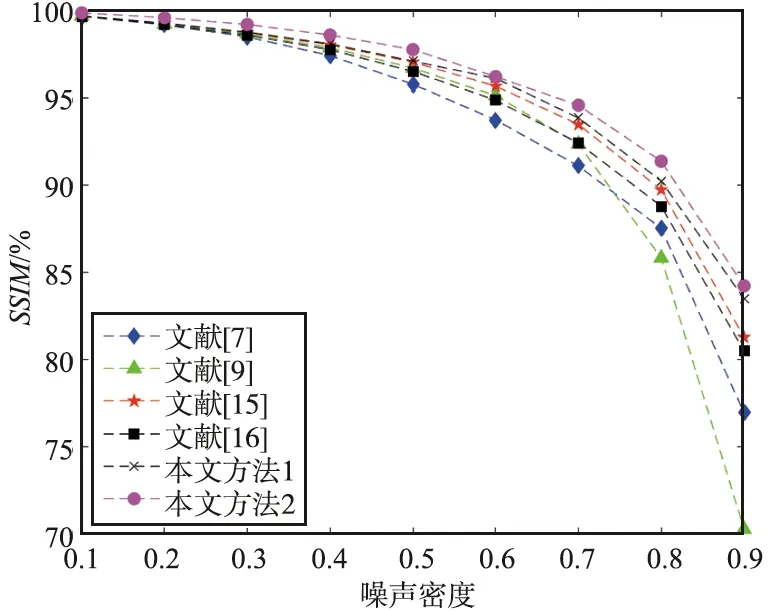
(a) SSIM

图6显示了各算法在图像test028上的去噪结果。图像test028的特色为具有大片的黑白区域。因此对该图像去噪的算法需具有鲁棒的噪声检测器，将黑白区域的无噪像素与噪声像素区分开，从而保持这部分像素的原始信息。明显地，从图6可以得出以下结论：① 文献[7]的去噪性能较差，未能有效恢复图像的纹理结构和边缘细节，另外，在噪声密度较高时，文献[9]的去噪性能骤然走低；② 文献[15-16]以及本文方法1的去噪结果相差不大，个别算法的SSIM值相对高一点，但EPI值又相对低一点，总体相差不大，因为这些都是最新提出的且具有相对良好性能的算法；③ 相对地，本文方法2的SSIM和EPI值一致地高于其他算法，体现了其更好的去噪效果和边缘恢复能力。原因在于本文方法2具有准确的噪声检测器和有效的后边缘增强处理。

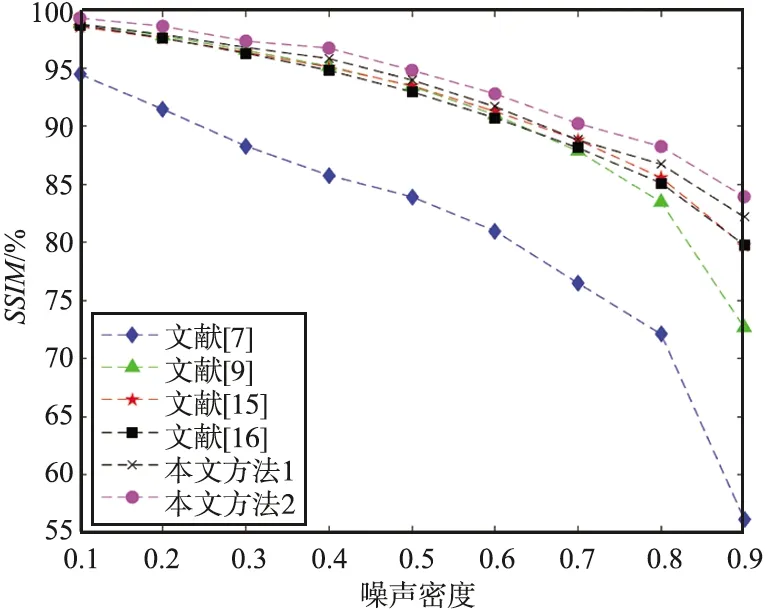
(a) SSIM

4.2 去噪图像

根据低密度噪声往往难以从视觉上区分各算法之间性能的优劣，因此，对于去噪图像视觉效果的比较，这里采用高密度噪声。各算法对含噪密度90%的图像parrot去噪的结果如图7所示。含噪如此之高的图像，从视觉上几乎看不出任何的图像信息了，但是各算法依然能从不同尺度上对其进行图像恢复，但效果有差别。很明显，文献[7,9]的去噪图像分别布满了黑色和白色的噪声板块，这是去噪不彻底造成的。根本原因在于其噪声检测器漏检了部分噪声像素，这部分噪声像素未能得到恢复处理。类似地，文献[16]的去噪图像也存在少量的噪声斑点。相对地，文献[15]和本文方法都能彻底去除噪声，并且整体图像较清晰。另外，对文献[15]和本文方法的去噪图像进行仔细比较，可以看出文献[15]去噪图像前景对象的外轮廓边缘和内部边缘细节呈现明显的锯齿状，部分边缘不连续，鹦鹉的眼睛丢失了。相对地，本文方法去噪图像的外部边缘与内部边缘都恢复得较好，边缘连续，锯齿状较轻微，鹦鹉的眼睛得到有效得恢复。

(a) 含噪90%的parrot

相对于其他图像，图像test011最能考验去噪算法的性能，因为图像test011具有大量的方格边缘，并有部分黑色区域。同样地，从含噪密度为80%的图像test011几乎看不出任何的图像信息，各算法在不同程度上对其进行了恢复，效果如图8所示。从图8可以得出以下3个结论：① 文献[9]的去噪图像呈现少量的噪声斑点，去噪不彻底；② 文献[7，9，15-16]都对图像中的方格边缘进行了恢复，但是边缘的锯齿状特别严重，右上方的部分方形窗格变成了三角形；前景人物的边缘的锯齿状也较为明显；③ 虽然本文方法的去噪图像也难免出现锯齿状，但是其程度相对较弱，基本上能保持方形窗格的形状，前景人物的边缘恢复效果比其他算法更好，图像的整体清晰度优于其他算法。

(a) 含噪80%的test011

4.3 算法的执行效率

算法的执行速度往往决定着一个算法的实用性和适用范围，现代图像处理亟需性能优越且实时执行的算法。为了验证各算法的执行速度，将各算法应用于各种含噪密度的数据集BSD68，然后将执行时间对图像数目求平均值，结果如表1所示。从表1可以看出，文献[7,15]的计算耗时较多，难以满足图像快速处理的要求。文献[9]的执行速度最快，完全达到实时的处理速度。文献[16]和本文方法的执行速度相当，当噪声密度不是很高时，可以实现图像的快速处理。虽然本文方法在执行速度上未能显示出显著的优势，但其执行速度相对于大部分的现有算法已经算是较快了。

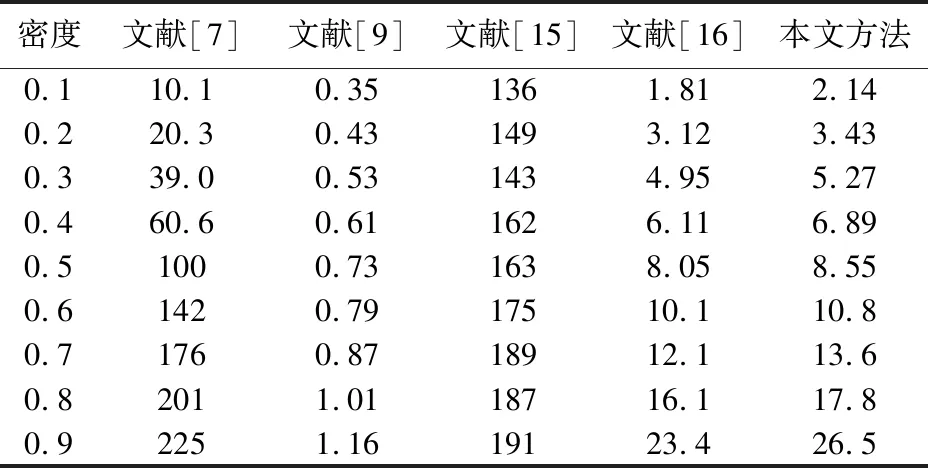
表1 各算法在数据集BSD68上的平均执行时间Tab.1 Average execution time of each algorithm on dataset BSD68 单位：s

综上所述，根据图像实验的客观结果SSIM和EPI、去噪图像的视觉感知以及算法的执行效率的比较分析，可以看出本文方法相对部分最新提出的现有方法具有更好的去噪性能，更好地保持和恢复图像的纹理结构和边缘细节，同时能实现图像的快速处理。

5 结束语

为了在去除噪声的同时，有效地保持和恢复图像的纹理结构和边缘细节，提出了一种带边缘增强的反比相对距离加权均值滤波方法。利用无噪像素的分布特性对噪声进行识别，用邻域像素的反比于相对空间距离的加权均值进行去噪处理，用拉普拉斯算子对去噪图像进行后边缘增强。实验结果证明，本文方法在去噪性能和边缘细节的恢复上优于现有算法，在算法的执行效率上优于大部分现有算法。虽然本文方法相对于现有方法的优势不是特别显著，但是其对于不同图像，均一致地取得最好的去噪效果。