5G MEC系统融合粒子群和教学算法的卸载策略优化

韩松岳，郭基联

(1.陆军工程大学 通信士官学校，重庆 400035；2.中国人民解放军32705部队，陕西 西安 710086；3.空军工程大学 航空工程学院，陕西 西安 710038)

0 引言

第五代移动通信技术(5G)采用新型网络架构，引入虚拟化和软件定义网络技术，网络功能与传统专用电信设备解耦合，转而基于通用服务器以软件包形式运行，实现了虚拟化、模块化和弹性化部署，从系统架构和网络功能层面赋予了5G开放、灵活的属性，使其成为了当前社会各行业信息化、智能化转型的平台技术。尽管5G性能参数和能效指标较4G实现了跃升，具有大带宽、高速率、广连接和低时延等特点，但是在自动驾驶、远程手术和虚拟现实等计算密集、时延敏感和数据隔离型应用时，仍需引入移动边缘计算技术(Mobile Edge Computing，MEC)作为辅助和增强，从而保证服务质量(Quality of Service，QoS)。

5G赋能的智慧教室作为智慧校园的核心应用场景，相较于传统的数字教室，教学设施和智能终端能够直接或通过5G CPE间接接入5G网络，赋能诸如Cloud VR/AR教学、学情大数据分析、课堂监控智能分析和超清远程直播课堂等新型教学应用。为此，在5G架构下部署MEC系统，任务数据能够在校园本地完成处理，相较于传统蜂窝网赋能的云计算智慧教室，节约了传输链路信道资源，大幅缩短了数据流转路径，避免了链路拥塞，从而降低业务交付时延和设备能耗，同时，数据不出园区带来的隔离特性，大幅降低实验数据、敏感信息和用户隐私的泄露风险。计算卸载作为MEC的关键技术，是指将任务处理过程按相应的卸载策略从移动设备迁移到资源充裕的其他设备上[1]。若缺乏适用于具体场景的卸载策略，系统会根据信道质量、网络信息和MEC资源可用性，随机卸载到通信质量好或计算资源充裕的MEC服务器，造成服务器过载，产生额外的时延和能耗，影响用户体验质量(Quality of Experience，QoE)。传统4G与MEC的融合部署，受限于4G架构和物理条件，需在网络架构中引入控制实体[2]，而5G架构部署MEC由于虚拟网元，因此可选策略更加灵活。

综上，本文在智慧教室场景下，以5G MEC系统作为信息服务的基础设施，开展系统构建和优化方法研究具有一定的现实意义。当前，业界学者区分不同卸载场景，针对不同优化目标建模开展了卓有成效的研究。Zhang等[3]提出了一种并行卸载模型和小区域卸载方案，Sun等[4]运用协同PSO解决无人机工业物联网资源分配问题，Ji等[5]运用强化学习解决了多用户单MEC场景的卸载优化问题；资源分配研究为所卸载任务分配算力资源[6]。因为卸载策略往往是多目标优化问题，所以上述研究运用到智能优化算法或机器学习算法求解问题，但是上述模型没有考虑到类似于智慧教室的固定场所场景下MEC系统中终端设备通常由稳定市电供能，不能仅考虑时延优化，还应防止“过载”现象发生，需在模型中加入相应的优化机制。为此，本文主要开展了以下工作：

① 开展基础理论研究，梳理5G MEC融合机制，结合应用场景构建5G MEC系统架构。

② 依托基金项目开展实验测试，指出高网络并发状态下，VR教学、专网视频会议和超清直播出现网络抖动和延迟增大的问题。

③ 基于贪婪思想[7]运用教学算法对粒子群迭代更新后的粒子，进行“教”阶段和“学”阶段更新，并利用贪婪原则进行迭代，提出融合教学机制的自适应粒子群(Teach & Learn Adaptive Particle Swarm Optimization，TLAPSO)算法，开展仿真实验，验证了其收敛性和复杂度的优化。

④ 将所提算法应用到系统模型中，与基于模拟退火算法、粒子群算法和本地卸载的策略进行对比分析，并取得了较优结果。

1 智慧教室信息系统模型构建

1.1 基于多视图方法论的需求分析

多视图方法论[8]是指从不同对象的视角对目标系统进行规范化描述，形成相应需求描述视图用以反映不同对象的诉求，最终形成完善的需求分析框架。

5G智慧教室包含的终端设备数量大、种类多，应用服务具有差异化网络诉求，网络服务呈大流量、高并发的特点，在建设与测试阶段，面临计算卸载决策触发机制可靠性低、卸载位置不合理和资源利用不充分等挑战。为此，需要研究适用于智慧教室场景的计算卸载策略。本文引入系统工程领域多视图方法论开展需求分析，形成了如图1所示的需求分析框架，用以指导后续系统架构设计和模型构建。

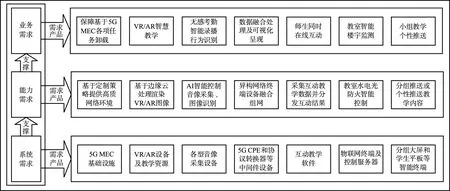
图1 5G智慧教室需求分析框架Fig.1 Requirement analysis framework of 5G smart classroom

1.2 系统构建和问题描述

以需求为牵引，本文构建了具有远程互动教学功能的5G智慧教室，系统架构如图2所示，具体包

图2 5G智慧教室抽象模型Fig.2 Abstract model of 5G smart classroom

含现场互动教学、远程互动教学、VR/AR教学和分组启发教学4种教学场景。

在实际运用中，智慧教室多场景、多应用交错运行，有大量网络需求各异的并行计算业务，因此，易产生较高的时延与能耗，QoS无法得到保证。尤其在VR/AR教学中，基本阶段的VR业务网络端到端时延需小于20 ms，才能确保虚实同步和避免眩晕感，而舒适和理想阶段需分别小于15 ms和8 ms时延[9]。然而，智慧教室多建于室内场馆，有稳定市电保障，因此，为进一步降低业务的交付时延，合理利用计算资源，本文以能耗约束条件下优化时延为目标，运用TLAPSO算法，基于MEC系统的数学模型对计算卸载进行优化。

算法中，粒子有速度和位置2个向量参数，分别表示粒子移动的方向、步长和潜在可行解，因此粒子编码的维度与计算任务维度相等，粒子位置向量的元素值表示MEC服务器的编码，最后通过算法迭代寻优，最终输出一个代表最优解的位置向量，即为卸载决策向量。

1.3 模型构建与目标确立

根据需求分析框架和智慧教室系统架构，本节就计算卸载过程进行建模，模型中的主要符号含义如表1所示。

表1 主要参数设置Tab.1 Main parameter settings

1.3.1 时延模型

当计算任务量较小时，任务在本地设备处理，产生本地计算时延Tl：

Tl=ci/fu,i，

(1)

式中，ci表示工作负载。fi表示计算密度，即单位数据量所需的CPU周期数，该值与任务类型相关。

当计算任务较大时，则卸载至MEC端处理，计算卸载包含上行传输、计算处理和结果反馈3个主要阶段，相应地产生传输时延、MEC计算时延和反馈时延。在5G架构中，下行链路数据传输速率快，体验速率有100 Mb/s，峰值速率达20 Gb/s[10]，且计算结果经过MEC端的编码压缩，使得数据量较小，因此反馈时延忽略不计，则计算卸载总时延Ti为：

Ti=Ttrans+Tcal，

(2)

式中，上行传输时延Ttrans可由上行传输链路速率Rij间接求得，根据Shannon-Hartley有：

(3)

Ttrans=ci/Rij。

(4)

而MEC端计算时延Tcal为：

Tcal=ci/fsi。

(5)

1.3.2 能耗模型

任务处理过程主要产生本地计算、上行传输和MEC计算处理3种能耗。其中，上行传输能耗面向终端设备，由终端发射功率求得：

Etrans=PiTtrans。

(6)

本地计算能耗为：

El=ku(fui)2ci，

(7)

式中，k是由芯片架构决定的能量系数，根据文献[11]的方法，本文终端设备ku=10-25；fui为终端设备的CPU周期频率，反映了终端设备的算力水平。

MEC端计算能耗为：

Es=ks(fsi)2ci，

(8)

式中，fsi为MEC服务器的CPU周期频率，同上述方法，MEC服务器能量系数ks=10-27。

1.3.3 确立优化目标

根据前述分析，智慧教室虽然有稳定的市电保障，但为防止高能耗对供电线路造成高压负载，避免对设备的生命周期造成损害，应控制卸载在能耗合理范围约束内。为此，通过增加过载后系统开销，建立防过载机制。综合时延与能耗模型，确立优化目标为在能耗约束下，求使得MEC系统时延最小化的卸载决策向量，表述为问题G：

(9)

其中，当任务在本地执行时，式(9)中p=0，并且：

Tl=ci/fu,i。

(10)

当任务卸载至MEC执行时，p=10-2.7并且：

Ti=Ttrans+Tcal，

(11)

s.t.

0≤Pi≤Pimax，

(12)

0≤fui≤fumax，

(13)

0≤fsi≤fsmax。

(14)

在问题G中，式(12)、式(13)和式(14)是面向任务处理全周期的约束条件，即终端发射功率应钳定在限额内，本地设备和MEC服务器的计算频率也应在算力的上限范围内。

2 融合教学机制和粒子群优化的TLAPSO算法

2.1 粒子群算法

PSO的寻优过程通过粒子在搜索空间的飞行完成，粒子每次迭代中的移动由3个部分组成：对上一次速度的继承、自身学习以及种群的信息交互[12]。其表达式为：

vi(k+1)=ωvi(k)+c1r1[Pbest,i(k)-xi(k)]+

c2r2[Gbest-xi(k)]，

(15)

xi(k+1)=xi(k)+vi(k+1)，

(16)

式中，ω为惯性权重系数；c1，c2表示学习算子，c1表示受自身历史最优影响程度的大小，c2表示受种群最优影响程度的大小，是控制PSO的迭代最重要参数；xi(k)表示粒子i第k次迭代的位置向量；vi(k)表示其速度向量；r1和r2为随机因子；Pbest,i为第i个粒子的历史最优；Gbest为种群最优[13]。

2.2 教与学算法

教与学优化(Teaching-Learning Based Optimization，TLBO)算法由Rao等[14]于2012年提出。相较于其他智能优化算法，TLBO具有收敛速度快、不依赖主观设置参数等优势。此后，多人对TLBO算法进行了改进。Li等[15]基于差分进化算法(DE)对TLBO进行了改进，形成混合自适应教学优化算法(ATLDE)，解决了光伏模型未知参数的识别问题。Chen等[16]通过构造自适应框架，将原始TLBO与高斯分布进行融合，新的更新律在搜索过程中以适应度对应的2种模式切换。此外，为了避免初始化过程中的局部收敛，引入了与原始教学和学习阶段相关联的自学习阶段。Ma等[17]引入新的种群机制改进了TLBO，提升了收敛速度和精度。李丽荣等[18]引入自适应因子提升TLBO的性能和精度。

TLBO算法主要是模拟以班级为单元的教学方法，班级中学生学习水平的提升需要通过老师的“教”来引导，同时，学员之间需要相互“学习”来提高对知识点的吸收。在该算法机制中，“老师”和“学生”充当了进化算法的种群个体，种群个体中适应度最好的个体充当“老师”身份，每个学员所学的某一科目都对应一种决策变量。具体表述如下：

③ 教学班：将该算法中搜索空间中所有点的集合称为班。

⑤ 老师：老师并不固定，而是教学班中成绩最好的学员，即Xbest，记作Xteacher。

2.2.1 “教”阶段

在算法的“教”阶段，教学班中每个学员Xj(j=1,2,…,NP)通过计算可以得知个体与班级平均值及教师的差距，并据此差距进行学习追赶。教学方法示意如图3所示。

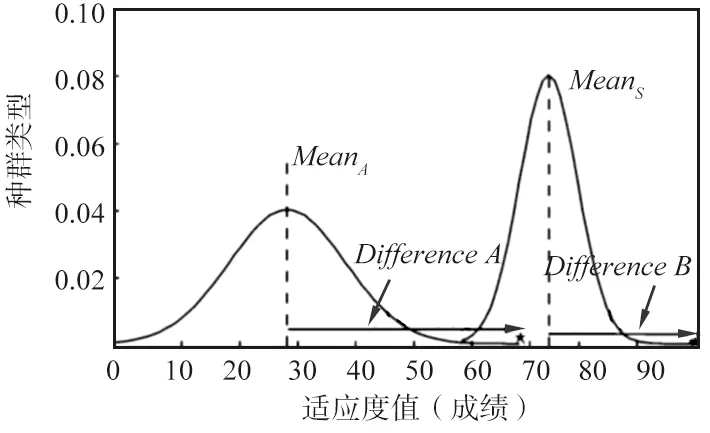
图3 教学方法示意Fig.3 Schematic representation of teaching methods

由图3可知，前期的班级平均成绩为MeanA=28，成绩分布区间跨度较大，通过老师反复教学，后期班级平均成绩有所提升，达到了MeanB=74，并且成绩分布区间跨度有所压缩。

在“教”阶段，学员通过学习来缩小与老师和学员平均水平之间的差距，该阶段可表示为：

(17)

Difference=ri(Xteacher-TFiMean)，

(18)

2.2.2 “学”阶段

该阶段与鲸鱼优化算法(Whale Optimization Algorithm，GWO)的随机搜索机制类似，通过让每个学员Xi(i=1,2,…,NP)将随机一个同学Xj(j=1,2,…,NP,j≠i)视作自己学习竞争的对象，学员Xi与其学习对象Xj进行对比，找到差距所在从而进行学习和追赶，其中，根据学习步长r对每个学员采用不同的学习因子，增加了种群的随机性，增强了算法摆脱陷入局部最优状态的能力。学习过程为：

(19)

式中，学习因子ri=U(0,1)表示学习步长。

2.2.3 迭代更新

更新方法IfXinewis better thanXioldXiold=XinewEnd if

2.3 算法融合改进

将粒子群更新后的粒子作为教与学算法的学员，利用教与学算法对粒子进行位置更新，TLAPSO算法流程如图4所示。

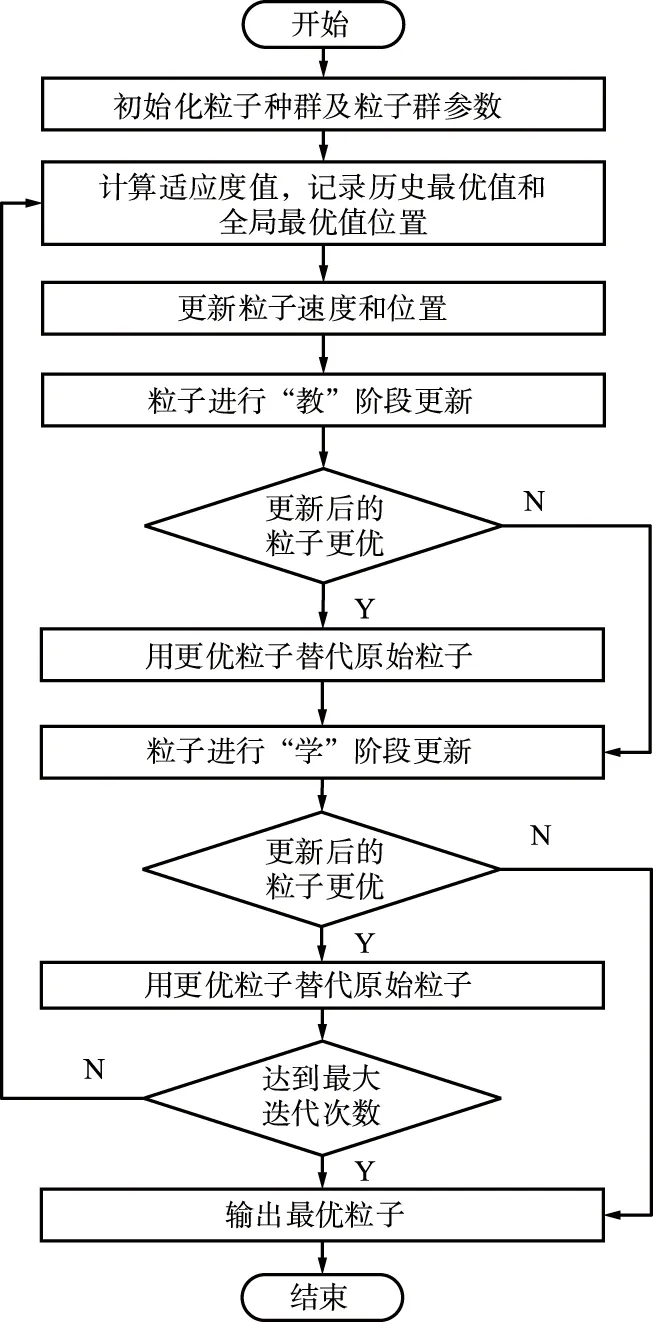
图4 TLAPSO算法流程Fig.4 Flowchart of TLAPSO algorithm

2.4 算法性能验证

基于仿真环境Intel Core i5 1.6 GHz处理器，内存16 GB的HUAWEI Matebook14，操作系统Windows10专业版64位，使用Matlab 2018b作为仿真平台，对融合教与学算法和粒子群算法的改进TLAPSO算法进行验证分析。

为验证改进算法的性能，确保算法的通用性和测试条件的完整性，基于单峰、多峰和混合维度多峰3类共23个测试基准函数，对TLAPSO与基本PSO算法开展仿真对比实验，并针对每个函数连续进行30次实验，将实验结果的均值以图表的形式直观呈现。表2给出了23个函数的表达式、变量取值范围、维度和最优值等参数。

表2 测试基准函数表Tab.2 Table of test benchmark functions

续表编号函数维度取值区间fminF21F21(x)=-∑5i=1(X-ai)(X-ai)T+ci[]-14[0,10]-10.153 2F22F22(x)=-∑7i=1(X-ai)(X-ai)T+ci[]-14[0,10]-10.402 8F23F23(x)=-∑10i=1(X-ai)(X-ai)T+ci[]-14[0,10]-10.536 3

将TLAPSO与基本PSO算法在上述测试基准函数上进行比较，设置种群数量为30，最大迭代次数为200，通过连续的30次实验，2种算法的最优适应度值、最优解对应的平均适应度值、最差适应度值、标准差和算法自用时间如表3所示。

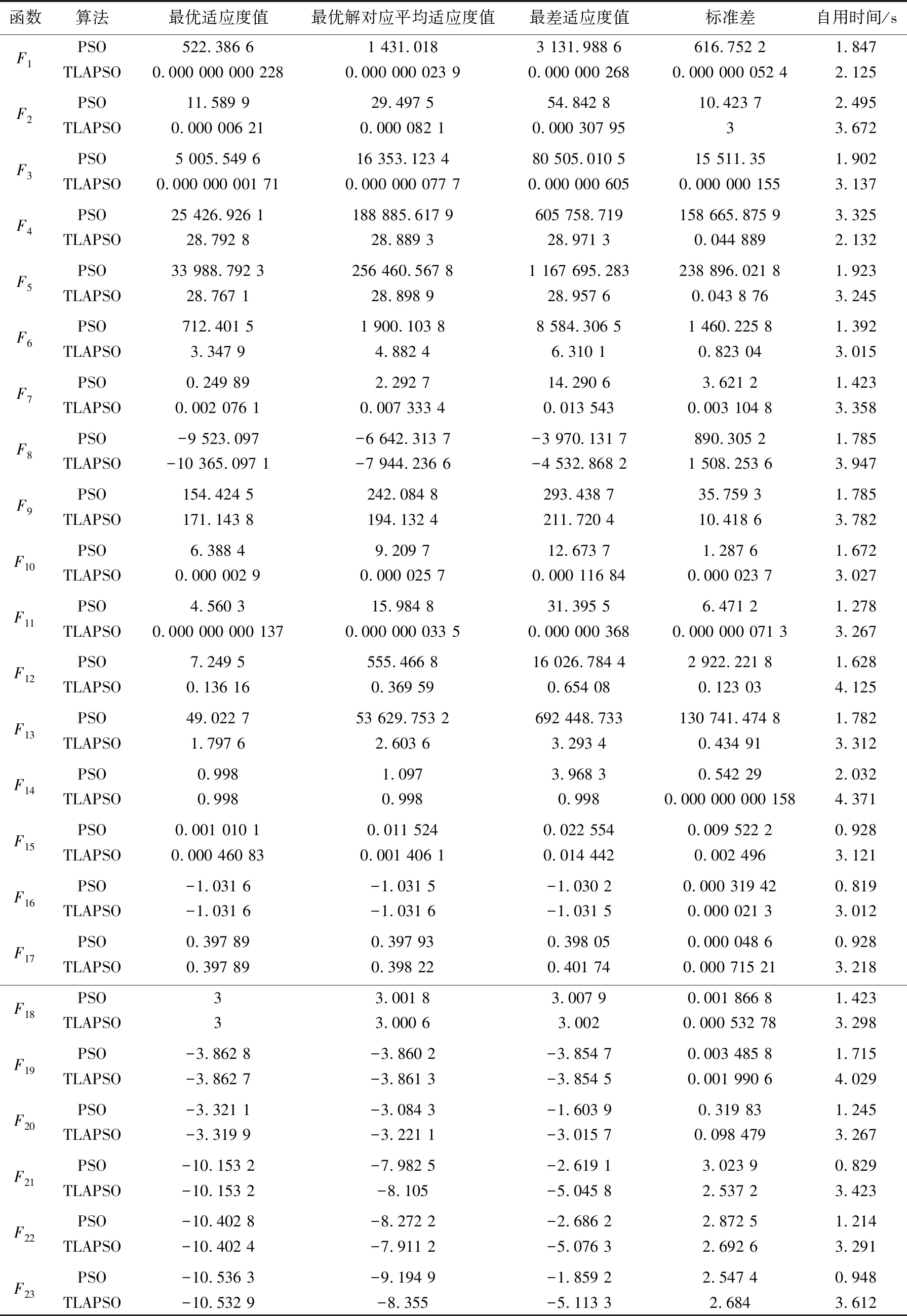
表3 PSO与TLAPSO算法在测试函数上的运算结果Tab.3 Operational results of PSO and TLAPSO algorithms on test functions

实验结果如图5和图6所示，图5分别是函数F1～F21的实验结果图，蓝色线条表示原始PSO算法的寻优结果，红色线条表示TLAPSO算法的寻优结果。从仿真实验图像看，在函数F1～F21中，改进TLAPSO算法表现均优于基本PSO算法，具有更快的收敛速度和更优的收敛精度，证明TLAPSO算法性能提升明显。

但是，图6中TLAPSO算法在F22和F23函数迭代后期，收敛精度略低于原始PSO算法，但收敛速度仍快于原始PSO算法。其中，在函数F22对比实验中，2种算法在迭代至第150次时，相互重叠并取得了相同的适应度函数，迭代至166次后，改进TLAPSO算法收敛精度略低于基本PSO算法；函数F23对比实验中，TLAPSO算法在迭代至131次时，与原始PSO算法出现交叉，并在后面的迭代中，收敛精度略低于原始PSO算法。

客观上，改进算法通常经过调整参数、融合更新机制或引入其他数学操作，流程上的增加必然导致算法调用和自用时间的增加。但是基于23个测试函数实验，连续进行30轮，每轮迭代200次算法自用总时间看，改进算法TLAPSO平均自用时间为3.339 s，PSO平均自用时间为1.579 s，复杂度虽较经典PSO有所提升，但收敛性能取得了较大的提升，因此TLAPSO在性能改进的基础上，算法复杂度得到了较好的控制。

由上述仿真实验可得,相较于原始PSO算法，TLAPSO算法在解决大部分单峰和多峰函数具有更快的收敛速度和更高的收敛精度，在部分高维问题上，会略微牺牲收敛精度，而取得更快的收敛速度。因此，TLAPSO算法在应对智慧教室中，入网终端设备和MEC服务器数量不大，且装备设施空间位置相对固定的场景时，能够取得较好的优化结果。

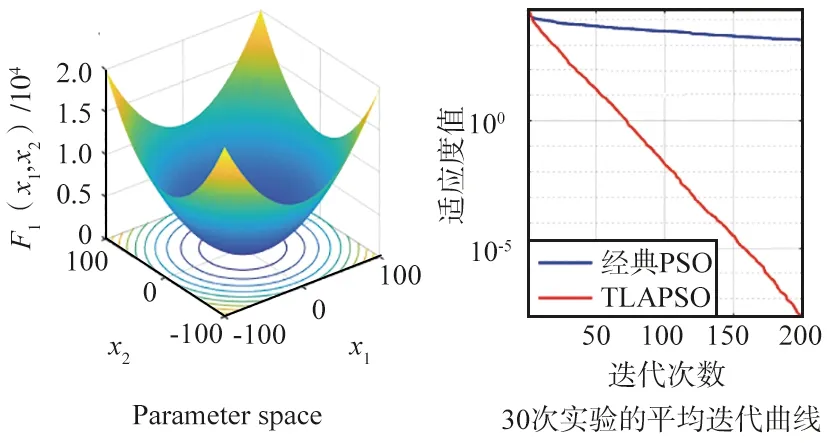
(a) F1

(a) F22

3 基于TLAPSO算法的计算卸载策略优化

3.1 粒子编码

本文基于整数编码，令种群数量为M，任务数量为K，MEC服务器的数量为N，用字母T表示计算任务task，则任务集合为T={T1,T2,T3,…,Tk}。其中，每个任务包含3个关键信息：处理任务所需的数据量、单位数据量所需的CPU周期和处理该任务的最大能耗约束。因此，用三元数组结构表示Ti(Bi,fi,Emax)，用字母S表示MEC服务器，则MEC服务器集合为S={S1,S2,S3,…,Sn}，用Hij(1≤i≤K,1≤j≤N)表示任务Ti卸载到服务器Sj的上行链路信道增益矩阵。

在本文依托的项目背景中，共有3个MEC服务节点为教学场所提供数据卸载分流服务，后期随着研究与建设的深入，可以对系统进行升级改造，主要节点采用实体MEC系统部署，其余的节点采用软件虚拟化形式的MEC与4G宏站、5G微站共站部署。假设一个智慧教室中某一时段共有9个大数据量业务需要卸载到MEC端进行处理。则任务集合可表示为T={T1,T2,T3,…,T9}，基于整数编码的方法，若粒子i编码为Xi=[1,3,7,0,2,5,4,2,0]，则表示任务T1卸载到编号为1的MEC服务器，任务T2卸载到编号为3的MEC服务器，任务T3卸载到编号为1(7-3-3=1)的MEC服务器，任务T4在本地终端设备执行计算处理。

粒子速度向量用来更新粒子的位置，由式(16)可知，对应于粒子的位置向量，速度向量表示粒子在空间中飞行运动的方向和跨度，其维度与粒子编码相对应，因此，每个维度的元素值表示任务卸载服务器编码位次的变化。

3.2 适应度函数

本文以智慧校园为背景，针对智慧教室作为应用场景进行建模，从前述分析可知，智慧教室有稳定的市电保障，因此，为降低模型和算法复杂度，进一步提升卸载效率，将模型简化为在能耗约束下最小化时延，并且当卸载任务产生的计算能耗大于能耗约束时，会增加卸载代价。因此，算法的适应度函数为：

(20)

3.3 基于TLAPSO算法的计算卸载流程

受教学活动启发，将“教与学”算法与粒子群算法相融合，通过收敛速度更快、寻优精度更高的TLAPSO算法解决计算卸载问题，结合图4所示的算法流程，步骤如下：

(1) 初始化

初始化种群及相关参数。赋予粒子随机位置和速度向量，设定种群规模M=30，MEC服务器数量N=5，加速常数c1=c2=1.5，惯性权重ω=0.8，为确保粒子不飞出边界而错过最优解，设定最大速度vmax=10，最大位置边界xmax=5，最大迭代次数设为150。

(2) 计算适应度值，记录历史和全局最优

基于给定的参数计算总时延和能耗，得出每个粒子适应度值。其中，历史最优值为从初始迭代到当前粒子所遍历的最好位置，可记为Pbest,i；所有迭代中的适应度值最优的粒子为种群最优值，记为Gbest。

(3) 粒子迭代更新

当迭代次数小于80时，则循环进行粒子“教”阶段和“学”阶段的迭代更新:

“教”阶段的位置更新为：

(21)

“学”阶段位置更新为：

(22)

速度更新时，当粒子速度超出速度最大限制，则用该速度作为最大速度边界值更新粒子速度。

(4) 用更优粒子替代原粒子

通过前面设定的参数值，计算粒子的适应度值，并遴选更优的粒子替代Pbest,i和Gbest。

(5) 停止准则处理

当达到最大迭代次数时，则停止更新，此时输出的卸载决策向量Vi即为所求的全局最优解，且适应度函数值为时延最小开销。在迭代中，若更新的粒子适应度值趋于平稳，不再有上下波动变化，则确定已找到全局最优解，停止更新并输出结果。

3.4 TLAPSO算法在MEC系统中的实现与应用

通过算法的迭代和寻优，在特定场景及其参数下，能够快速得出全局最优的卸载策略。可以通过在系统中引入控制实体，将基于TLAPSO算法的卸载调度策略写入调度模块，实现卸载策略的应用，也可以将基于优化算法的卸载策略通过API接口写入MEC系统层的编排器中，实现基于特定策略的计算卸载。

4 仿真实验及对比分析

4.1 环境搭建及参数设置

基于与3.4节中相同的平台环境进行仿真。为进一步量化评估部署MEC系统后，业务时延的改善与优化，对比应用不同卸载策略的效果，遴选出适用于智慧教室场景的卸载策略。根据前述模型和问题G，对基于本地卸载执行(未部署MEC系统)、TLAPSO算法、基本PSO算法和SA算法的卸载策略进行仿真实验，对比分析上述4种卸载策略的性能，给出部署MEC系统对5G智慧教室网络承载优化程度的定性评价，以及采用不同卸载策略对5G MEC系统优化改善的定量评估。仿真实验参数设置如表4所示。

表4 主要参数设置Tab.4 Main parameter settings

4.2 仿真实验设计

4.2.1 任务量实验

本实验以终端设备的任务量为变量，以MEC系统在能耗约束下的卸载总时延作为系统总开销，衡量不同卸载策略在相同参数环境下的收敛性能。设置相关参数如下：MEC服务器数量S=8，终端设备产生的任务数一共有T=60个，任务量分别设置为[5，10,15,20,25,30,35,40,45,50] MB，仿真结果如图7所示。

图7 任务量实验结果Fig.7 Experiment results of task volume

从仿真结果看，本地卸载策略在实验初始阶段任务量较小的情况下，相较于将计算任务卸载到MEC服务器，有较大的卸载开销。同时，随着任务量的增加，本地卸载策略的系统总开销增幅最大，足以证明在智慧教室部署MEC系统能够有效地降低业务交付时延，提升用户体验。此外，基于SA算法的卸载策略在实验任务量较小的初始阶段，系统总开销略高于基于PSO算法的卸载策略，经过分析推论为在处理低维度问题时，复杂度较高的SA算法给系统造成了额外的时延，但在任务量适中的场景下，优化效果好于PSO算法，在任务量较大的场景下，优化效果与PSO接近。基于TLAPSO算法的卸载策略在任务量较小时优化效果并不明显，但随着任务量的增加，优化效果远优于其他卸载策略，即TLAPSO卸载策略在大任务量场景中的优化效果更加明显。

在该实验中，TLAPSO卸载策略对系统的优化程度最大值在任务量为50 MB时，较本地卸载策略优化提升了55.90%。

4.2.2 能耗容忍度实验

虽然智慧教室有稳定的市电供能，但是随着智慧校园形态的发展演进，未来将融入更多的物联网和移动互联网终端设备，并且智慧化教学手段不再局限于教室，而是向室内外联动教学和异地智慧化教学演进[19]。因此，在室外条件下的供能与能耗，将直接影响到室外教学条件的构设、供能方式的优选和终端设备的寿命周期。

为了拓展TLAPSO卸载策略的适用场景，本实验通过控制设备产生的任务数量、MEC服务器数量和任务量大小3个变量，增加能耗容忍条件限度，观察不同卸载策略的表现。设定参数如下：MEC服务器数量S=8，终端设备产生的任务数一共有T=60个，任务量大小为5 MB，仿真结果如图8所示。

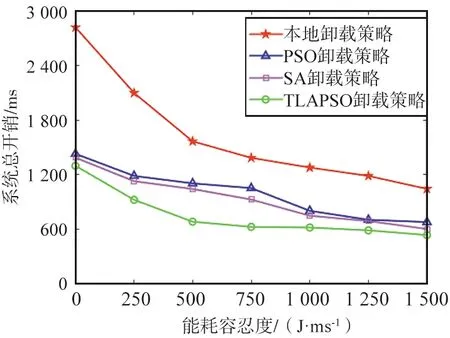
图8 能耗容忍度实验结果Fig.8 Experimental results of energy consumption tolerance

从仿真结果看，随着能耗容忍度的增加，系统总开销呈递减趋势。其中，本地卸载策略卸载总开销远高于其他卸载策略，并且前期能耗容忍度不高时，开销减小速度快于后期，因为终端设备的CPU算力有限，超过其上限后，即使再增加能耗容忍，终端设备的敏感度也会降低，同样说明了将任务卸载到MEC服务器处理的必要性。此外，SA卸载策略与PSO卸载策略优化效果接近，TLAPSO策略优于其他卸载策略。

在该实验中，TLAPSO卸载策略对系统的优化程度最大值在能耗容忍为0 J·ms-1时，优化率达54.02%。

4.2.3 MEC服务器数量实验

该实验以待处理的任务总量为变量，分别设置5台和10台MEC服务器，都以TLAPSO卸载策略进行仿真实验。设置参数如下：任务总量分别设置为[300,600,900,1 200,1 500,1 800,2 100,2 400,2 700,3 000] MB，仿真结果如图9所示。

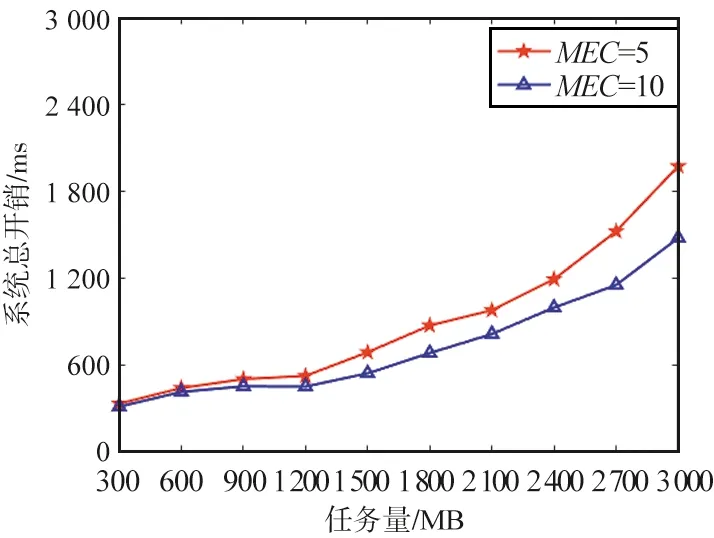
图9 MEC服务器数量实验结果Fig.9 Experimental results of the number of MEC servers

从仿真结果看，随着待处理任务总量的增多，蓝色折线上升趋势变缓，并且系统总开销始终低于红色折线，说明MEC数量增多，不仅MEC端整体算力有所增强，同时粒子寻优的可行解维度也有所增加，计算任务根据距离、MEC服务器算力性能和信道质量等因素，可选的服务器更多。此外，本文中的模型设置了防过载机制，能够有效防止计算任务过多卸载至通信和计算资源条件更优的服务器上，杜绝因过载而产生额外的能耗和时延。

4.3 结论分析

从上述4种卸载策略的仿真实验结果看，在5G网络架构中部署MEC系统，能够有效降低系统总开销，优化智慧教室场景中的业务交付时延，提升QoE。同时，基于TLAPSO算法的卸载策略相较于本地卸载、PSO和SA卸载策略具有更高的卸载效率，能够更好地提升系统效能。

在智慧校园的发展演进中，随着入网设备的增多，海量数据的本地云化处理需求相应地提升，应当以现有网络基础设施为依托，以教学科研和校园治理业务需求为牵引，基于校园布局、路测数据和网优规划手段，增加MEC节点数量，但是由于当前5G MEC实体服务器成本高昂，可以考虑以少量实体服务器为中心，分布式部署虚拟化MEC节点，实现过渡阶段的平滑演进，满足智慧校园个性化业务的差异化网络需求。

5 结束语

以5G智慧教室为应用场景，对计算卸载的优化问题进行了研究。首先，归纳了5G与MEC的融合部署方式、分流机制和卸载决策，梳理了近年来实用的群智能优化算法，基于多视图方法论开展了需求分析。其次，构建了基于5G MEC技术的智慧教室系统架构，并对优化目标进行了建模，结合课堂教学过程的启发，提出了TLAPSO算法，通过仿真实验，证明了改进算法性能的提升。最后，基于实验数据，对比分析了多种卸载策略的效果，从定性和定量两方面验证了智慧校园中部署MEC系统的必要性，以及TLAPSO卸载策略的优越性。

今后将针对MEC集群化部署、卸载策略的前端实现和基于深度学习的优化策略开展研究，以实体或软件包的形式实现算法优化套件，提升系统简洁运维、优化策略快速上线和MEC系统的综合效能。