筑坝堆石料仓面图像分形特性与评价
马明刚 沈超敏 严良平 潘月梁 周 浩 彭泽豹 徐 琼
(1.宁海抽水蓄能电站有限公司,浙江 宁波 315699;2.河海大学 水利水电学院,南京 210024)
堆石料是指通过爆破或者开挖得到的岩石颗粒集合体.由于其良好的力学特性和经济适用性,被广泛应用于土石坝、机场高填方等重要基础设施工程中.堆石料颗粒的粒径跨度从毫米级到接近米级,跨尺度的颗粒相互填充,对堆石料的物理力学行为造成深刻影响:拥有优良级配曲线的堆石料大小颗粒内部填充充分,通常呈现较高的密度和较好的强度变形特性[1-2];反之级配较差的堆石料由于内部颗粒填充性较差,不仅密度和模量无法满足土石坝设计要求,且在水头梯度作用下易发生坝料渗透破坏等问题[3-4].因此,《碾压式土石坝设计规范》(SL 274—2020)规定土石坝的坝料级配需在设计的上下包络线内,并结合施工阶段的检测保证堆石料的级配符合设计要求.目前堆石料级配的检测主要通过在土石坝施工现场开挖密度坑,并在现场进行堆石料的颗粒筛分试验得到.尽管堆石料的筛分试验原理和操作流程均不复杂,但试验通常采用人工筛分,试验过程费时费力,成为掣肘土石坝机械化施工效率的重要因素之一.
虽然筑坝堆石料的颗粒粒径大小不一,坝料的级配在空间上分布也并不均匀,但堆石料的级配曲线通常存在不同尺度的自相似性.Burn[5]研究这类不同尺度上存在的自相似性,并提出了分形理论.近年来,分形理论在水利岩土领域的土体裂隙分布[6]、颗粒破碎后的粒径分布[7]、岩石表面以及界面的粗糙度[8]等方向得到了重要的应用.国内外学者针对颗粒材料级配的分形特性也做了许多重要的工作,例如Sammis等[9]针对断层泥筛分后发现其级配曲线符合分形特性,即其级配曲线可以用P(d)=(d/dM)3-D表示,式中:d为颗粒粒径;dM为最大粒径;D为级配曲线的分形维数;Coop等[10]根据钙质砂在环剪过程中的破碎规律,发现经过充分破碎后,钙质砂的级配会趋于分形分布,且分形维数D=2.59;吴莹等[11]收集了不同堆石坝工程的堆石料级配曲线,发现其级配曲线均具有较好的分形特征,且分形维数大多在2.3~2.7之间.朱晟等[12]分析了不同分形级配筑坝料的压实密度和强度变形特性,并据此提出了堆石料级配的优化设计方法.
在土石坝工程中,筑坝堆石料填筑铺层图像是从仓面的表观“窥见”其颗粒分布的重要渠道,目前有一些学者尝试通过数字图像处理技术检测其级配曲线[13].然而由于表观图像颗粒重叠、光源的均一性等问题,精确地区分复杂光源条件下堆石颗粒的边界还有进一步完善的空间.级配描述的是堆石料颗粒大小的分布规律,其本质是颗粒集合体的一个几何特征.由于具有自相似特性的集合,在仓面的投影也应当具有自相似性,因此本文尝试直接研究堆石料铺层仓面图像的分形特性,并据此评价堆石料的级配特性.
1 堆石料仓面分形特征提取
1.1 仓面图像获取与预处理
采用的堆石料填筑仓面图像来自某抽水蓄能电站的上库主坝施工现场,上水库大坝为混凝土面板堆石坝,最大坝高63.6 m,坝顶长度587 m,坝顶宽度8 m.上库坝料岩性主要为库内石料场开采的新鲜或强~微风化祝村组蚀变玻屑凝灰岩、凝灰岩、含砾玻屑凝灰岩.为了获取堆石料铺层足够具有代表性的图像,图像获取的时间选在铺层完成后碾压前,图像获取方法采用无人机悬停后拍照,无人机采用DJI Mavic系列,悬停高度离仓面5 m,光圈f/2.8.采用无人机获取堆石料填筑仓面图像的过程如图1所示.

图1 基于无人机的堆石料填筑仓面图像获取
无人机获取的堆石料仓面图像像素尺寸为4 000×3 000像素的彩色图像,如图2(a)所示.首先将RGB三个色彩通道的图像通过浮点法转化为灰度图,得到的灰度图如图2(b)所示.然后基于Otsu[14]二值化方法提取灰度阈值,将灰度图转化为二值化的图像,如图2(c)所示,以便提取堆石颗粒的边界纹理特征.

图2 填筑仓面图像预处理
1.2 仓面图像获取与预处理
堆石料填筑仓面图像分形维数的计算方法并不唯一,本文采用盒子维数的方法计算求解,其基本原理是:根据图像的长宽比选取特征尺寸为Δ的长方形“盒子”去覆盖图像(如图3所示),此处长方形盒子的长宽比与整体图像一致;统计特征尺寸为Δ的“盒子”内包含了颗粒的边界(黑色像素)的数目N(Δ),则如果该图像本身存在自相似性,其分形维数为
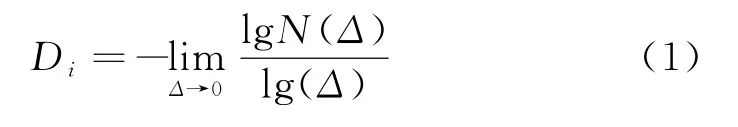

图3 填筑仓面图像的“盒子”覆盖
图4采用了两种不同的归一化阈值将堆石料的某仓面灰度图进一步转化为了二值化图像.第一个归一化阈值为0.5,与Otsu法得到的阈值0.49较为接近,得到的二值化图像中黑色像素点相对较多,即保留了较多的颗粒表面杂质和光照阴影等“噪点”信息;第二个归一化阈值取0.4,二值化后图中的黑色像素相对较少.针对上述两张二值化图像,根据式(1)的“盒子”维数法在双对数坐标下绘制了N(Δ)和Δ关系曲线,可以发现两者基本平行,换言之,堆石料图像的分形维数受二值化阈值的影响较小.因此,下文的图像处理统一采用Otsu法得到的二值化阈值.

图4 二值化阈值对图像分形特性的影响
图5选取了抽蓄主坝的某填筑仓面中4个典型图像,采用上述方法分析了仓面图像的分形特性,并提取了分形维数值.可以看出,仓面不同位置的堆石料图像N(Δ)和Δ在双对数坐标下均存在较为显著的线性关系,表明堆石料填筑仓面图像在不同尺度内有自相似性,即图像具有典型的分形特征.

图5 填筑仓面分形维数计算
2 试验结果与分析
本文在堆石料的填筑仓面开展了5组密度坑试验,碾压仓面上试验坑选取位置由人为随机选取.在实际检测过程中,人为选取的密度坑一般需要考虑测点的代表性,尽量选取视觉上判断细料含量适中的位置开展坑测试验.图6(a)为5个试坑的实测级配曲线,可见不同测点之间的级配差异较小,且均在设计规定的上下包络线之内.图6(b)进一步在双对数坐标下绘制了这些实测的级配曲线.

图6 填筑仓面的坑测级配曲线
可以看出,这些级配曲线在双对数坐标下近似符合线性分布规律,级配曲线为

式中:dM为试样的最大粒径;D为试样级配的分形维数.根据图6(b)的结果可知,这些试坑的级配分形维数D约为2.56.
仓面的图像纹理分析采用无人机获取,无人机悬停在某一固定高度后,针对该抽水蓄能电站的上库主坝某仓面拍摄了247张照片,并根据这些图像计算了各自的图像分形维数值D i.图7为该仓面图像分形维数的频数分布图.

图7 填筑仓面的图像分形维数频数分布
从图中可以看出,堆石料仓面图像的分形维数主要分布在1.4~1.9区间内,且D i取值在1.6~1.75之间的占比较大,越偏离该区间则分布的数量越少.图7中的光滑曲线为采用正态分布曲线拟合该频数分布的结果,正态分布拟合的均值μ=1.68,标准差σ=0.099 7,总体上填筑仓面图像的分形维数值统计上服从正态分布规律.图7进一步给出了3张典型的不同分形维数的堆石料图像,图像位置的横坐标对应了该图像的分形维数区间,从图7可以较为明显地看出,随着图像分形维数的增加,其细料含量也逐渐增多.因此,采用填筑仓面的分形维数作为指标,可以较好地检测堆石料颗粒的整体粗细程度.
图8中的圆形标记给出了无人机拍摄图片中的GPS坐标信息,且根据这些测点的D i插值,得到了仓面的堆石图像分形维数空间分布云图.

图8 填筑仓面的图像分形维数空间分布规律
从图8可以看出,土石坝的填筑仓面级配分形维数存在显著的空间变异性.沿着纬度方向的D i值变化较小,而沿着经度方向则存在条带状分布:D i在经度51.8″~52.2″范围内的取值在1.5~1.7之间,处于细料含量较为适中的区间,而在经度52.4″~52.8″范围内D i取值在1.7~1.8之间,属于细料含量较高的材料.其主要原因是施工填筑的顺序是沿着纬度方向连续填筑,经度一致、纬度相邻的区域料源大体相近.
对比坑测的级配结果(图6)和图像分形维数结果(图7~8)发现:1)因为级配曲线的分形维数D(式(2))和填筑仓面图像的分形维数D i(式(1))定义不同,其实测结果也存在差异,从现有的数据结果看D比D i约大1,且随着D或者D i的增大,堆石料的细料含量增多;2)颗粒筛分试验得到的级配曲线差异性显著小于图像识别得到的全仓面图像纹理分形的差异性,原因可能是颗粒筛分试验得到填筑仓面少量测点的级配曲线有较大概率处于正态分布概率最大的区域,并不能真实反映全仓面的堆石料级配曲线分布情况.
3 结论
基于无人机和数字图像技术,研究了堆石料填筑仓面图像的分形特性,并结合填筑仓面密度坑的颗粒筛分结果,探讨了采用仓面图像分形值描述堆石料级配信息的有效性和优势.主要结论有:
1)无人机在固定的高程悬停可以获得相较于手持式拍摄范围更广、区域更固定的图像,且分辨率能够满足堆石料填筑仓面的图像纹理分析需求;
2)筑坝堆石料填筑仓面的图像存在显著的分形特性,其分形值可以通过对图像进行灰度化、二值化,并采用“盒子”维数法求解获取;
3)堆石料图像的分形值D i是描述填筑仓面堆石料的细料含量的有效指标,且统计上符合正态分布规律;
4)相较于坑测颗粒筛分法获得的级配曲线,采用图像的分形维数D i作为级配评判指标,具有快速无损、且可获得堆石料细料含量空间分布规律等优点.
需要说明的是,本文提出的图像分形维数D i是评价其粒径分布规律的重要指标,但目前还不能取代规范要求的现场颗粒分析试验.由于本文的研究还处于初步应用阶段,如何建立堆石料级配曲线的分析维数D和仓面图像的分析维数D i之间的定量关系还有待进一步研究;如何将堆石料级配的空间变异性反映到坝体的变形与渗流稳定的计算分析中也是需要进一步探索的课题.

