基于“导问”的高中数学教学设计策略

朱晓祥

高中数学教学应以发展学生数学学科核心素养为导向，创设合适的教学情境，启发学生思考，引导学生把握数学内容的本质。导问式教学是以“导问”为特征的一种课堂教学活动，是以“问题链”的形式，让学生在学习中层层交流、深入思考，进而能主动发问。导问式教学设计的问题应该具有以下三个特点：一是具有引导意义的问题情境；二是有目的地发展学生的认知策略；三是让学生感知数学方法论的出发点。因此，导问式教学方式有助于发展学生的创新思维能力，培养严谨求实的科学精神，树立敢于质疑、善于思考的批判性思维意识。下面，笔者以具体的教学实例，谈一谈如何设计基于“导问”的高中数学课堂教学。

一、以“问”导“建”，在自主建构概念中培养学生的创新思维能力

数学概念是揭示现实世界空间形式与数量关系本质属性的思维形式，是数学知识的基本单元。因此，在概念教学中，通过“导问”引导学生积极参与数学概念的建构过程，有利于学生更好地理解其实质，也有利于对学生科学思维能力的培养。笔者在执教人教A版高中数学必修第二册第六章第一节“平面向量的概念”时，进行了以下探索和思考，与同行们交流。

笔者认为，本节课的目标主要有三个：一是让学生抽象出向量的基本概念、基本表示、研究特殊向量之间的基本关系；二是理解平面向量的几何意义和代数意义，体会数形结合的数学思想；三是让学生体验研究新概念的基本思路和内容，即通过类比、抽象、概括、归纳、实践等途径，研究一个新概念的定义、表示、关系和应用。因此，在设计“问题链”时，应该设置有引导意义的问题情境，通过启发式的引问帮助学生建立认知结构。

【教学片段一】

问题1：如图1，若小正方形的边长为1m，一只蚂蚁沿直线从A爬行到B，再从B爬行到C。蚂蚁爬行的距离和位移分别是多少？

问题2：距离和位移有什么不同？

（图1）

问题3：位移作为一个物理量，它同时包含大小和方向两个要素，请列举生活中的位移。

问题4：这一类对象的共同属性是什么？你能用数学的语言概括“向量”的概念吗？

问题5：在数学学习的过程中，我们有没有学过既有大小、又有方向的量？

问题6：我们学过类比数、集合、函数的研究方法，接下来我们应该从哪些方面研究向量这一新的概念？

问题1从实际生活中的情境出发，引导学生感悟两个不同的概念，引出向量概念的原型；问题2培养学生的抽象概括能力和语言表达能力；问题3引导学生观察、概括，得到概念的本质属性；问题4引导学生自主生成概念；问题5将物理模型数学化；问题6在问题5的基础上层层设问，让学生体会研究概念的基本途径，培养学生的科学思维。

基于问题解决取向的教学模式，强调在教学过程中利用“问题链”将学生的概念表象与原有经验联系起来，在设置导问和问题解决过程中给学生更多的独立空间。在教学中，处于中心地位的应该是通过问题解决的过程发展学生的元认知策略、认知结构和相应的学习态度。

二、以“问”导“思”，在自主解决问题中培养学生的科学思维方式

美国心理学家纽厄尔与西蒙（Newell ＆Simon）提出：问题是这样一个情境，个体想做某件事，但不能即刻知道做这件事所需采取的一系列行动。［1］当学生遇到难度较大的数学题时，需要有适切的解决问题的策略和合理而科学的思考过程。在这个过程中，教师通过“导问”提出具有探究性的问题，将突破点设置在学生的思维最近发展区，调动其解决问题的欲望，这有助于培养学生的自主意识和创新意识。

数学问题解决的过程应该分为以下五个阶段。（1）理解问题：什么是未知的？什么是给出的？（2）问题表征：代数表征和几何表征是什么？（3）拆分成子问题。（4）实施：确定计算和推理过程。（5）反思：问题的内涵和外延。

在人教A版高中数学选择性必修第一册第二章“直线和圆的方程”的学习中，学生遇到这样一个问题：已知a＞0，过点P（a，3a）的直线l与x轴、y轴交于A，B两点，且△AOB面积为83，这样的直线有4条，求a的取值范围。

这道题对学生来说有一定的难度，其难度来自两个方面：一是与学生既定状态已掌握的知识和技能的联系较少；二是题目的表征形式的一般化程度不高，具有一定的抽象性。基于这样的情况，笔者设置了以下导问路径。

【教学片段二】

问题1：已知条件是什么？求什么？

问题2：过一点的直线由什么元素确定？

问题3：怎样从代数的角度表达“这样的直线有4条”？

问题4：（追问）你能够构建解题过程吗？

问题5：怎样从几何的角度表达“这样的直线有4条”？

问题6：同学们是否记得在之前的学习过程中我们做过这样一道题：过点P（2，23）的直线l与x轴、y轴的正半轴交于A，B两点，求△AOB面积的最小值及此时直线的斜率。

问题7：我们能否将点P一般化，得到一般性结论？

在这个问题链中，问题1、2是提出问题，问题3是代数表征，问题5是几何表征，问题4是选择解决问题的一个策略，问题6是局部启发，问题7是反思和应用。本教学环节以问题为起点，以探究为路径，创造适合学生思考的合作环境，从而唤起学生对问题及其本质的探究欲望。

三、以“问”导“问”，在自主发问中培养学生的批判性思维意识

在数学教学中，我们不仅要让学生成为“问题解决者”，还要让学生成为“问题发现者”，让学生主导问题的提出、问题的分析、问题的解决三个课堂环节。

1.引导学生追因索果，由疑生问

在数学教学过程中，我们希望学生对所学的知识和方法，不仅要知其然，更要知其所以然。因此，在教学过程中，要让学生学会多问为什么，努力激发学生提问的意识。

【教学片段三】

在二项式定理的教学中，有这样一道课外习题：求（x--1）4的展开式中的常数项。这道题目的难点在于，学生的认知里只有“二项展开式”，而没有“三项展开式”。

师：有没有同学能自主编拟一个类似的问题？

生2：求（x--1）4的展开式中的常数项。

在处理这个问题的过程中，生1的方法通过多项式乘法原理解决问题，其实是对二项式定理的认知，体现了较强的元认知能力和批判性思维能力。学生2改编的变式题拓宽了“三项”向“二项”转换的途径，体现了较强的创新意识。学生在自主发问和反思中探究了这一类问题的本质——“三项”转换为“二项”。

2.引导学生自编习题，由问生思

问题解决是一个发现、探索和创新的过程，包括提出问题、建构模型、设计方法、检验反思等。学生作为课堂的主体，应成为问题的发起点和终结点，让学习真正发生。在课堂上引导学生自主发问甚至是自主编题，有利于培养学生的高阶思维能力和批判性思维。

【教学片段四】

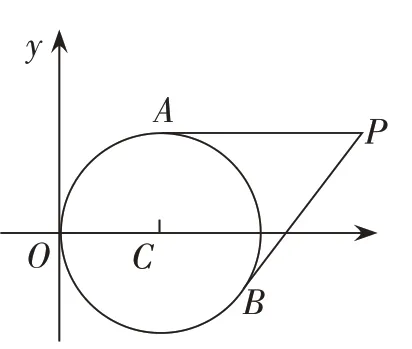
在“直线和圆的方程”单元复习课中，笔者编制了这样一道复习题：过点P（3，1）作圆C：（x-1）2+y2=1的 两 条 切线，切点分别为A，B，求切线PA的长。

师：以此为条件，你认为我们可以研究哪些问题？请你把问题编写完整，并尝试解答。

（图2）

生1：求线段AB的长。

生2：可以从角度看，求∠APB的大小。

生3：还可以从面积的角度探究，求四边形PACB的面积。

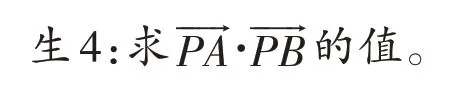
师：总结一下，刚才四位同学分别从几何图形中的线段长度、角度大小、面积大小、向量数量积四个方面编制了四个题目，请同学们课后自行完成这四个题目。这是一个几何图形中的定态问题，有没有同学可以将这道题目改编成动态状态下的取值范围问题？

生5：可以将点改成动点，点P为直线x+y-4=0上的动点，过P点作圆C：（x-1）2+y2=1的两条切线，切点分别为A、B。

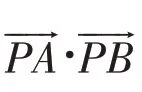
（学生完成练习）

师：点P是一个动点，它使得图形中一些几何元素的取值发生了变化，从而产生了以上一些有关取值范围问题。同学们能否探究一下，当点P在直线上移动时，几何图形中是否有确定的量或者几何元素？编制一道定点定值的习题。

生6：可以探究直线AB是否过定点以及△PAB的外接圆是否过定点。

在数学学习中，要彻底理解一个数学问题，就要弄清楚它的“来龙去脉”。在平常教学过程中，尤其是章节复习课和习题课中，教师首先应留时间给学生，鼓励学生大胆尝试，增强学生的学习信心和发问意识；其次是要把握好问题的“发问点”，精心挑选题干，让学生有题可编，有问可发，从而使学生的发问意识、批判意识在数学课上得到锻炼和提升。

新课程强调对学生创新意识和创新思维的培养。在数学课堂教学中，教师要关注与创新相关的能力和素养的培养，比如独立思考的能力、发散性思维、逆向思维等，关注学生发现问题和批判性思维的能力，培养学生探索新方法、积极主动解决问题的能力，摆脱思维定式，勇于创新。通过“导问式”的课堂模式，引导学生思考，培养学生的关键能力和核心素养。