一道解三角形多选题的赏析

张宁宁

(山东省济南市章丘区第四中学)

多选题是近年新高考数学试卷中出现的一种新的题型,该题型具有一定的综合性,注重对学生知识、方法的考查,对解题能力的要求较高.基于此,现选取一道解三角形多选题进行剖析,旨在帮助学生提高综合运用能力,增强运算求解能力以及推理论证能力.

1 问题展示

题目 已知在△ABC中,角A,B,C所对的边分别为a,b,c,且a＝6,4sinB＝5sinC,以下四个命题中正确的是( ).

A.△ABC的面积的最大值为40

B.满足条件的△ABC不可能是直角三角形

C.当A＝2C时,△ABC的周长为15

D.当A＝2C时,若O为△ABC的内心,则△AOB的面积为7

分析 本题主要考查解三角形与其他知识的综合运用,具体涉及正弦定理、余弦定理、三角形面积公式、三角函数、一元二次方程有实数根等,侧重考查学生的数学运算、逻辑推理能力,解法灵活多样,具有较强的综合性.

2 解法赏析

因为4sinB＝5sinC,所以由正弦定理得4b＝5c,从而可设b＝5x,c＝4x(x＞0).

2.1 分析选项A

2.2 分析选项B

因为a＝6,b＝5x,c＝4x,所以假设△ABC是直角三角形,则必有斜边a＝6,或者斜边b＝5x.

若斜边b＝5x,根据勾股定理得16x2＋36＝25x2,解得x＝2,此时△ABC的边长分别为6,10,8.

综上,满足条件的△ABC可能是直角三角形,故选项B错误.

2.3 分析选项C

方法1 当A＝2C时,cosA＝cos2C＝2cos2C-1.在△ABC中,由余弦定理得

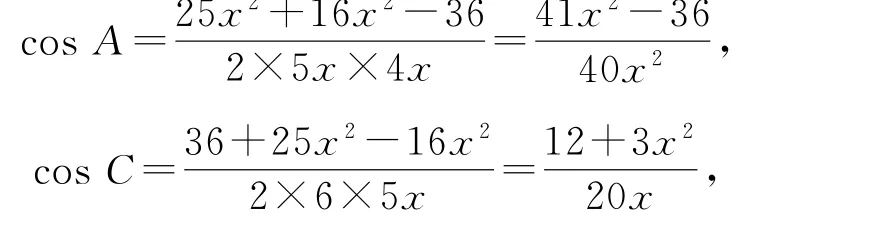
所以

解得x＝-1(舍)或1,从而a＝6,b＝5,c＝4,所以△ABC的周长为15,故选项C正确.

2.4 分析选项D

综上,通过对四个选项的逐个分析可知四个命题中正确的是ACD.

3 归纳总结

2)处理“不可能”问题时,需要灵活运用“假设法”——先假设可能,再进行合情推理、分析.若推出矛盾,则假设错误,即不可能;若推不出矛盾,则得到可能的具体情况.

3)求△ABC的周长时,方法1 是将二倍角余弦公式与余弦定理进行了综合运用,运算量较大;而方法2综合运用了正、余弦定理以及二倍角正弦公式,相对简单一些.

总之,该题设计较好,不但能够有效考查学生对相关数学知识和方法的理解、掌握以及运用程度,而且充分体现了多选题的特征——具有一定的综合性,对运算求解能力、推理论证能力也提出了较高要求,能够较好地培养学生的数学核心素养.

链接练习

1.(多选题)已知△ABC,角A,B,C所对的边分别为a,b,c,则下列条件一定能够使△ABC为等腰三角形的是( ).

2.(多选题)已知a,b,c为△ABC的三内角A,B,C的对边,下列命题中正确的是( ).

A.在△ABC中,sinA＞sinB的充要条件是A＞B

B.在锐角△ABC中,sinAsinB＞cosAcosB恒成立

C.若acosA＝bcosB,则△ABC必是等腰直角三角形

D.若B＝60°,b2＝ac,则△ABC必是等边三角形

链接练习参考答案

1.ACD. 2.ABD.