利用自注意力机制优化费米网络的数值研究

王佳奇，高泽峰，李永峰，王 璐

（1.内蒙古科技大学理学院，内蒙古包头 014010；2.中国人民大学理学院，北京 100080）

多电子系统的理论计算一直是物理学基础研究的重要课题.理论上，如果能够给出系统的波函数，则可由波函数得到系统的所有性质.但多电子系统的薛定谔方程难以直接求解，为此研究人员提出了多种各有优劣的近似求解方法，如常用的密度泛函理论[1-3]受交换关联能项的近似限制，在计算相互作用复杂的多电子系统时，精度无法满足计算要求.耦合簇方法中的CCSD（T）（coupled cluster with single，double and perturbative triple excitation）方法[4]可以得到精确的结果，但所用计算资源与基函数数目的7 次方成正比，造成CCSD（T）几乎不可能计算大分子系统.量子蒙特卡罗方法（quantum Monte Carlo method，QMC）[5]的计算精度很高，但结果收敛很慢，计算误差的衰减速度是计算时间平方根的倒数，要得到精确度足够高的结果所花费的时间代价无法接受.这些传统近似求解方法的求解精度和计算速度虽然在缓慢进步，但远远无法满足人们的需求.

近几年，人工智能在图像识别和语音识别等多个领域取得了突破性进展，并广泛应用于物理和化学等学科的研究中[6-10]，取得一定成果.如人们使用受限玻尔兹曼机拟合晶格体系的基态及含时演化过程[11-12]，其基态结果的精度可与耦合簇方法相比；对于小分子系统，人们使用神经网络作为变分量子蒙特卡罗方法的波函数试探解，并通过优化神经网络得到系统的基态能和基态波函数[13-15]，结果比传统变分蒙特卡罗方法更精确.其中，费米网络[13]仅使用电子及原子核的位置关系作为神经网络的输入，实现了对费米子系统的计算，给出了具有相同自旋电子的交换反对称波函数，并在小分子系统的计算中达到了非常高的精度. 因此，研究费米网络有助于更有效地定量研究费米子系统的性质.

近年来，相较于多层神经网络等以往常用的结构，在人工智能各个领域广泛应用的自注意力机制（self-attention）[16]展现出更强的表达能力.基于自注意力机制的Transformer 结构被应用于自然语言处理，如BERT（bidirectional encoder representations from transformers）[17]和GPT-2（generative pre-training）[18]中，并取得了良好效果.Transformer 结构成为提高现有工作精度和准确性的首选工具之一.本研究在保证系统费米子交换反对称的前提下，添加Transformer 结构，改变费米网络仅有的单一线性连接结构，以期增强网络的表达能力，新网络结构被称为Transformer-FermiNet（TFN），并在此基础上分析整个神经网络的物理内涵，对比不同Transformer 结构的表现力.

1 多电子系统

对于多电子系统，哈密顿量可以写为

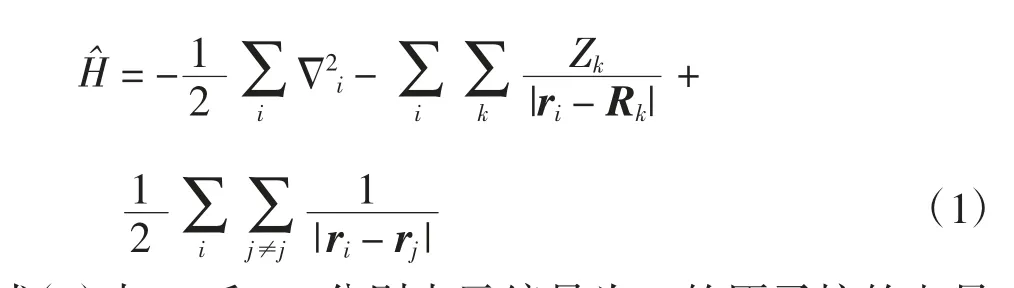
式（1）中：Zk和Rk分别表示编号为k 的原子核的电量和位置；ri和rj分别表示编号为i 和j 的电子的位置.式（1）右侧第1 项表示电子的动能，第2 项表示电子与原子核之间的相互作用，第3 项表示电子间的相互作用.基于波恩奥本海默近似（Born-Oppenheimer approximation），原子核的位置为给定的参量.理论上，将哈密顿量代入薛定谔方程的线性组合给出变分法的试探波函数.式（3）中：φkm为单电子轨道波函数，角标m=1，…，n 为不同的轨道，n为电子数，其中有n↑个电子自旋向上，有n↓个电子自旋向下，n = n↑+ n↓；Φk为由元素φik（xj）组成的矩阵；ωk为电子波函数ψ 用不同行列式det|Φk|展开的系数，k=1，2，…，K 为正整数；表示单电子波函数的一种排列；sign（）给出排列的奇偶性，为奇排列时，sign（）取负数，为偶排列时，sign（）取正数.（x）i表示在某排列下，xi变为（x）i=xj.斯莱特行列式的维数等于电子的个数，其展开后的项数随电子数增加呈指数级增长.对于多电子系统，求解这样的波函数极其困难，即使全结构相互作用求解方式在最近有了新的进展[19]，也只能计算为数不多的小分子.

选择1 个优秀的试探波函数可以加快变分法迭代的速度，且更容易得到高精度的近似解.在量子蒙特卡罗计算连续空间多体问题时，通常选用Slater-Jastrow 作为试探解[5，20].其主要思想是将斯莱特行列式截断，并添加Jastrow 系数项做近似.近年来，研究人员选用神经网络作为变分蒙特卡罗的试探波函数.由万能逼近定理[21]可知，多层神经网络能够以任意精度逼近目标函数，波函数也不例外，利用神经网络优秀的表达能力，良好地逼近复杂的波函数.文献[13]提出的费米网络正是对上述想法的实现.

2 费米网络

2.1 费米网络的基本结构

费米网络的细节非常丰富，为方便讲解TFN，在此对费米网络进行简要介绍，详细讲解可见文献[13].费米网络的结构如图1 所示，图1 上半部分表示神经网络的输入，下半部分展示了神经网络中单电子流与斯莱特行列式的连接及网络的最终输出.

图1 中，神经网络的输入分为2 个部分，上半部分的输入为电子-原子核之间的位置关系，称为单电子流.h0n层中，dnNx、dnNy和dnNz分别表示第n 个电子与第N 个原子核间位矢在三维空间的3 个投影，|dnN|则为这个距离的绝对值.下半部分的输入为电子-电子之间的位置关系，称为双电子流.与单电子流同理，电子i 和电子j 间的位置关系均用二者距离在三维空间中的3 个投影rijx、rijy和rijz及其绝对值|rij|共4 个量来表示.文献[13]强调，添加距离的绝对值能够大幅提高网络的学习精度及训练效率.这是因为三维分量与其所对应的位置关系是一体相关的，而神经网络无法准确地自我优化学习到这种关联，所以人为添加距离的绝对值是必要的.在单电子流和双电子流中，人为将自旋向上r↑和自旋向下r↓的电子分离输入.在最后1 个隐藏层hLn的输出中，自旋向上和向下的数据流分别对应网络后边的2 个行列式.费米网络在每一层中不断将双电子流信息混入单电子流中，最后将单电子流的输出组合成行列式det↑和det↓的形式，对多个行列式求行列式值并线性组合，得到神经网络最终的输出，即系统的波函数ψ.

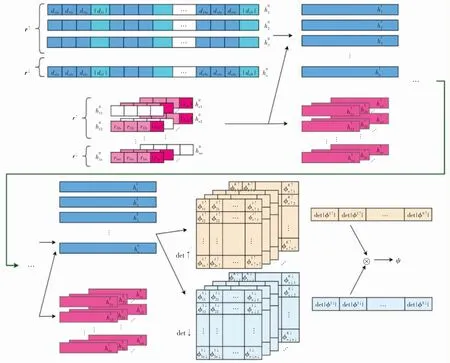
图1 费米网络结构Fig.1 Structure of the FermiNet

费米网络的训练分为2 个步骤：①使用Hartree Fock 理论计算结果作为标签值，使用Adam 算法[22]进行有监督学习的网络训练，称为预训练过程.预训练可以将网络参数优化到真实波函数的附近，减少网络陷入局部最优的可能性.预训练损失函数为

②将系统能量的期望值视为损失函数，使用经过优化的KFAC（Kronecker-factored approximate curvature）算法[23]最小化系统能量.电子的初始位置正态分布在原子核周围随机生成，在随后的迭代过程中，电子位置使用蒙特卡罗方法根据神经网络波函数给出.

2.2 费米网络的基准测试

为加深对费米网络的理解，本文首先计算一些已有结果. 根据电子数由少到多，选择计算LiH、NH3、CH3NH2和C2H5OH 共4 种分子，并比较计算结果.预训练的结果如图2 所示，其纵坐标用log10标度.

图2 不同分子预训练损失函数的对比Fig.2 Comparisons of the loss functions from pretraining for different molecules

由图2 可以看出，只有4 个电子的LiH 的预训练损失函数收敛得非常快，在1 000 步时，其损失函数已经降低至0.001 以下.而电子数为26 的C2H5OH 在1 000 步时，其损失函数稳定性较差，且下降速度缓慢.造成二者收敛速度不同的原因是电子数越多，其在空间中的态密度分布越复杂.因此，在预训练过程中，当系统的电子数较多时，应使用足够多的预训练步数使损失函数降到一个合理的范围，以保证预训练效果.图3 为不同分子基态能随正式训练步数的下降趋势.由图3 可以看出，4 条能量下降曲线在形状上相似，但前3 条曲线下降趋势不明显，尤其是LiH 对应的基态能下降曲线几乎为一条直线，而电子数为26的C2H5OH 系统的基态能表现出明显的不稳定. 由此可知，系统的电子数越少，神经网络给出的系统基态能收敛越快，且数值相对稳定.随着电子数的增加，需要拟合的目标波函数变得复杂.神经网络需要使用更多的训练步数使能量逐渐收敛，并改善网络输出的数值稳定性.

图3 不同分子正式训练所得系统基态能Fig.3 Ground energies of different molecules from training

为精确对比本文与文献[13]中费米网络的计算结果，给出正式训练20 000 步时，二者平均能量的具体数值列，结果如表1 所示.表1 中的CCSD（T）使用了CBS（complete basis set，CBS）基底集，能量单位为Hartree.

表1 本研究与文献[13]计算结果的对比Tab.1 Comparisons of the results of this study and reference[13]

在计算如LiH 和NH3等电子数较少的小分子时，费米网络对计算资源的要求不高，可达到很好的精度.但当计算如CH3NH2和C2H5OH 等电子数较多的分子时，利用现有计算资源所得结果与准确值存在一定差距.原因主要有两点：①有限计算资源下，较大batch size 的并行训练无法实现，但选用大batch size 可以有效降低能量值的波动性并加快训练速度.②对于较大分子，并未使用足够长的时间等待能量的进一步下降.

文献[13]中，费米网络在计算多电子系统，如甲烷、乙烯、甚至30 个电子的双环丁烷时，多数情况精度可以比肩甚至超越变分量子蒙特卡罗方法和耦合簇方法等传统方法，并在描述氢分子链及氮气的解离能方面表现良好.但费米网络的缺点也很明显，在现有技术手段下，费米网络的误差收敛到化学精度以内所花费的计算资源随电子数的增加呈指数级增长.如LiH 等小分子的计算仅需使用一张Nvidia 1650 GPU，其计算结果在几小时内即可收敛；但在计算双环丁烷时，需要使用16 张V100 GPU 进行计算，并花费约1个月的时间，才得到97%准确率的结果[13].目前，多数研究组难以获得这样规模的计算资源.

3 TFN 网络

3.1 TFN 网络结构

本研究使用的Transformer 结构包含自注意力机制和线性连接结构2 个部分，结构如图4 所示.图4中红色和绿色部分均代表可训练的参数，其中，自注意力参数的下标q、k 和v 分别源自自然语言处理问题中的query、key 和value，线性连接参数的下标lc 表示linear connection. 网络中可训练的参数包括自注意力机制所用到的权重Wq、Wk和Wv以及线性连接部分的权重Wlc. 本研究在网络中不同位置添加不同的Transformer 结构，但均基于图4 结构的微调.

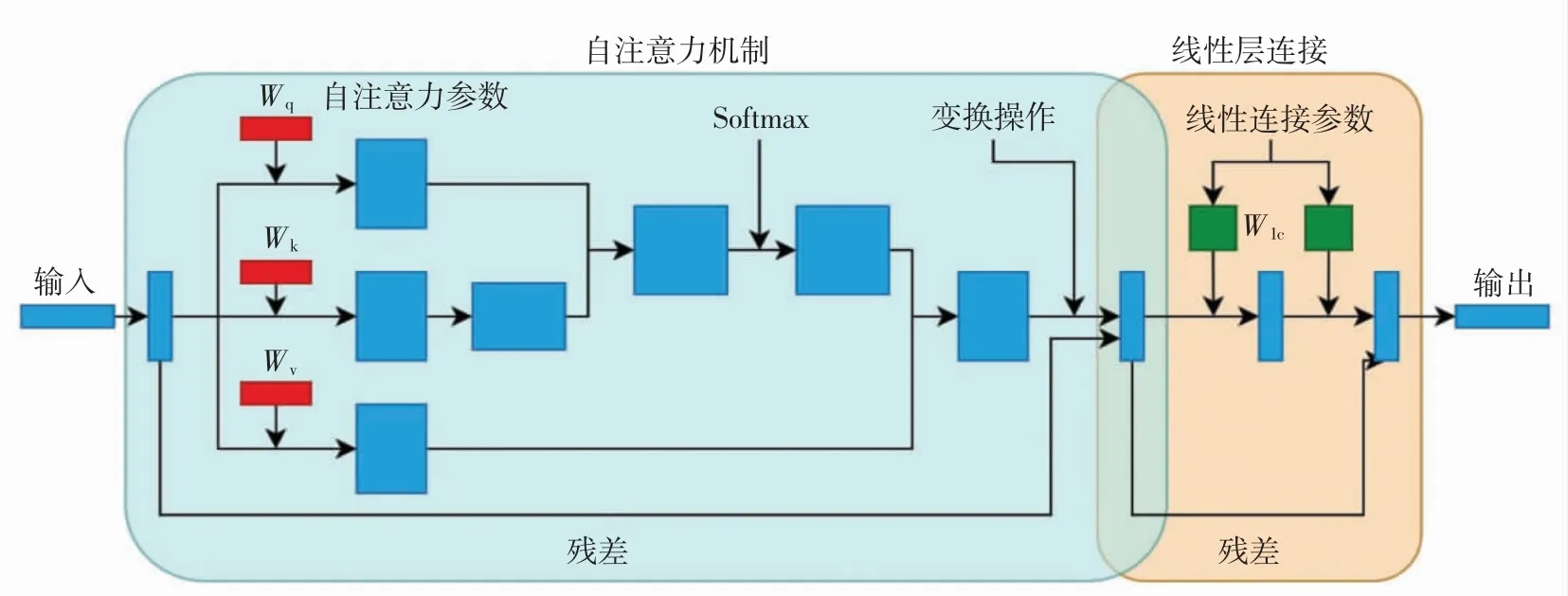
图4 Transformer 结构图Fig.4 Transformer structure

本研究在费米网络中使用了3 种Transformer 结构，添加位置分别在单电子流的输入层和中间层以及双电子流的中间层，每种添加方式均有其对应的物理考虑.

（1）选择对单电子流输入层中的电子-原子核距离的绝对值添加Transformer 处理，相当于额外分配参数用于专门学习电子与原子核间距的绝对值对波函数的贡献，这种添加了Transformer 的网络结构称为HT（head transformer），结构如图5 所示，图5 中深蓝色和蓝绿色部分分别代表电子-原子核位置关系的三维投影和绝对值.在同一个分子中，以甲烷（CH4）为例，其原子核中C 和H 所带电量不同，与电子的相互作用强度也不同，在输入层添加额外的Transformer 结构有助于学习到这种差异，因此，可将HT 视为一种额外的数据处理.

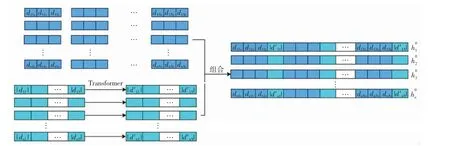
图5 HT 结构图Fig.5 Structure of the HT

（2）将单电子流中间层的连接方式完全改为Transformer，从而改变原有费米网络单一的线性连接结构，称为ST（single stream transformer）.图6 分别展示了单电子流和双电子流的Transformer.

（3）将双电子流中间层的连接方式完全用Transformer 替换则为DT（doublestreamtransformer）（图6（b）），这种替换方式与单电子流完全一致.由于许多新奇复杂的物理性质与电子-电子间相互作用有关，因此，使用更强表达能力的网络学习双电子流的信息是必要的. 需要注意的是，DT 中的Transformer 结构并没有用来强化学习不同电子与同一电子间的关联，这是因为不同于电子与原子核间的作用，由于电子所带电量相同，所有电子-电子相互作用均可视为使用同一种相互作用规则，没有必要额外添加Transformer 结构进行学习.

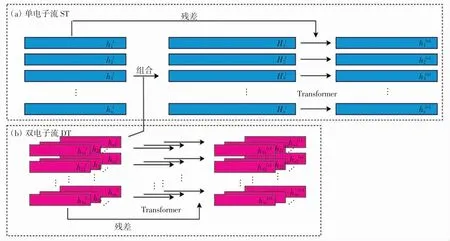
图6 ST 和DT 结构图Fig.6 Structure of the ST and DT

此外，本文在处理HT 中自注意力机制的结果时并未使用图4 中的求平均操作，而是使用打平操作（将结果矩阵按选定维度首尾相接成低维矩阵，称为flatten）.这样做的目的是为了更多地保留自注意力机制中的信息，满足HT 中对电子-原子核距离绝对值的强调. 对ST 和DT 中自注意力机制结果的处理使用了图4 中的求平均操作，这样做可以减少线性连接部分的参数数量. 修改后网络的优化过程依然符合预训练和正式训练梯度下降的算法要求（Adam 和KFAC），因此，TFN 所使用的优化方式与原费米神经网络相同.

3.2 TFN 的自对比

为研究Transformer 结构包含的自注意力机制和线性连接这2 种不同结构的参数对网络拟合能力的影响，以HT 计算甲烷（CH4）基态能为例，分别对比了Transformer 结构中参数的影响.为突出Transformer 结构本身的表达能力，网络的中间连接仅使用了2 层线性连接的隐藏层.每个隐藏层中单电子流使用32 个隐藏单元，双电子流使用8 个隐藏单元.

首先，使用固定数量的线性连接隐藏单元，并逐级增加自注意力机制参数的数量.图7 为TFN 拟合所得体系基态能与自注意力机制参数数量的关系.图7中，绿点代表在网络计算的基态能优化到稳定值后，分段截取数据并取平均，红点代表对整体的平均（对绿点求平均）.第1 组数据的自注意力机制隐藏单元数为4，线性连接隐藏单元数为8.后续计算中，线性连接隐藏单元数量保持不变，自注意力机制参数数量逐步由4 增加到256.

由图7 可以看出，当自注意力机制的参数数量较少时，网络的拟合能力较差，计算结果非常不稳定，表现为多个高能量点.随着自注意力机制参数的增加，网络的稳定性和精度均得到明显改善.但不断增加自注意力机制参数的数量并不能持续改进结果.在自注意力机制参数数量达到256 个时，虽然计算结果的精度依然小幅提升，但计算的收敛速度明显减慢.此外，图7中常出现一些偏离整体的值，如自注意力机制参数为64 个时，所得极个别能量值甚至高于参数为32 个时的能量值，这些值导致整体平均能量有所上升，但依然低于参数为32 个时的平均能量. 本研究仅对单层Transformer 结构内部参数进行了对比，而实际计算中则需使用多层网络，因此在计算资源有限的情况下，使用32～128 个隐藏单元即可得到较理想的训练结果.

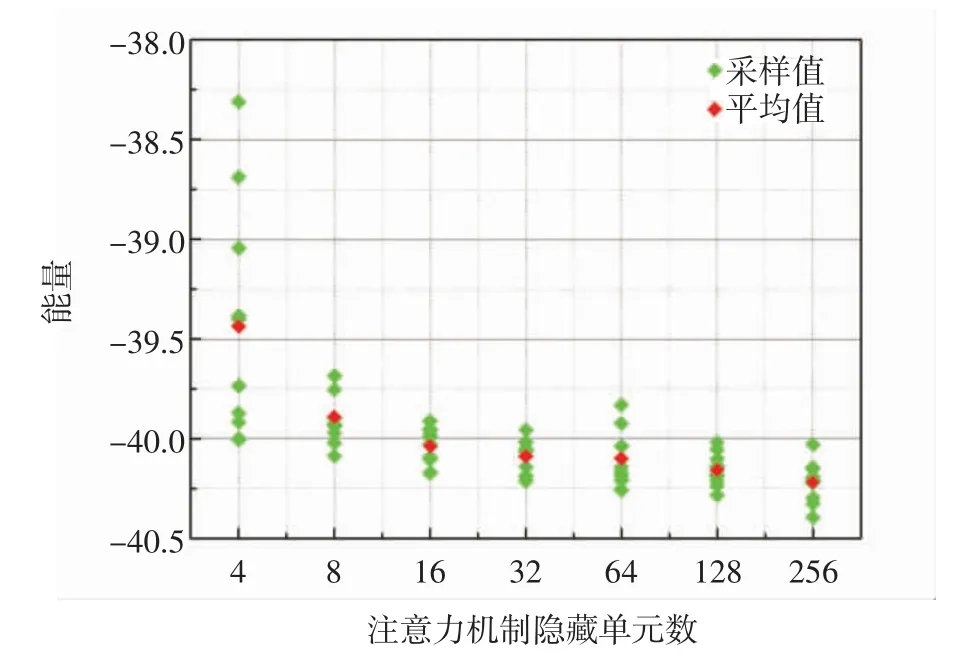
图7 自注意力机制隐藏单元数量对TFN 表达能力的影响Fig.7 Influence of the number of self-attention hidden units on the expressive power of the TFN

图8 为TFN 拟合的体系基态能与线性连接隐藏单元数量的关系，其中绿点、红点以及第1 组数据的选取方式同图7.后续计算中，自注意力机制参数数量保持不变，线性连接隐藏单元数逐步由8 增加到256.此外，图8 中隐藏单元数由64 增加到256 的过程中，网络的精度依然小幅提升.

由图8 可以看出，随着线性连接隐藏单元数量的增加，网络的精度和稳定性均逐步提升.但相较于128个隐藏单元，当隐藏单元数量增加到256 个后，所带来的精度提升已经很小.因此，在线性连接中使用64 或128 个隐藏单元是对计算速度和计算精度平衡后不错的选择.

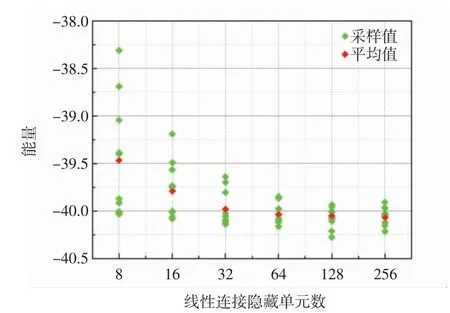
图8 线性连接隐藏单元数量对TFN 表达能力的影响Fig.8 Influence of the number of linear connection hidden units on the expressive power of the TFN

需要注意的是，线性连接的参数是1 个二维矩阵，而自注意力机制的参数是3 个一维矩阵.显然随隐藏单元数量的增加，线性连接参数数量的增长速度是自注意力机制参数数量增长速度的平方量级.即对比线性连接结构，自注意力机制的参数越少，表达能力越强.

为了统一对比，在对比Transformer 结构内部参数的所有计算中，使用的并行训练个数batch size=20，预训练次数= 1 000，正式训练次数= 40 000，学习率lr = 0.000 1，随着训练（step）的进行，学习率以lr（1/（1.0+（step/1 000.0）））的方式衰减.图7 和图8 中，计算数据在均值附近表现出显著偏离的现象主要是因为网络的训练过程使用了较小的batch size.在计算资源充足时，使用较大的batch size 可以使数据偏离的程度降低.原则上，使用大的batch size 能够得到精度和稳定性更好的结果.

3.3 TFN 的计算和参数讨论

为了展示添加Transformer 结构对神经网络表达能力的影响，以氨气（NH3）的计算为例，对比TFN 和标准费米网络的优化过程，结果如图9 所示.图9 中，纵坐标ΔE 为神经网络计算所得能量与CCSD（T）/CBS方法给出的能量之差，并用log10标度；横坐标中能量为分阶段取平均的结果，横轴上1～1 000 为每10 步对ΔE 取平均，1 001～10 000 为每90 步取平均，10 000 后是每100 步取平均.此外，为了满足大分子的计算需求，如计算30 个电子的双环丁烷以及26 个电子的乙醇时，文献[13]中的费米网络采用了固定数量的隐藏单元.但经过测试，在计算较小的分子时，适当削减网络的隐藏单元数量对结果精度的影响可以忽略.受限于计算资源，本研究主要用10 个电子左右的小分子进行计算.为了方便对比，费米网络的参数量被控制在与TFN 相近的范围.图9 中，TFN 和费米网络训练状况的对比被分为3 个阶段.在1～1 000 步的第1 阶段，TFN 和费米网络均在尝试快速将能量下降，但费米网络由于参数较多，下降得更加流畅连贯.经历第2 阶段（1 001～10 000步）时，二者均开始逐渐稳定到平衡值附近.在第3 阶段（10 000 后），二者的平均能量基本不再下降，且结果的波动性逐渐变小.随着后期参数的学习率减小，结果的波动性会进一步降低，在此阶段，TFN 和费米网络的表现相似.即在正式训练时，经过前期快速的参数调整阶段后，TFN 的表现能力与费米网络相似.为了清晰对比费米网络与TFN 的计算结果，从图9 第3 阶段后期的收敛结果中截取数据并取均值，结果如图10 所示.由图10 可知，在随机的抽样对比中，TFN 数据偏离均值程度略大，但其均值与费米网络结果相当.

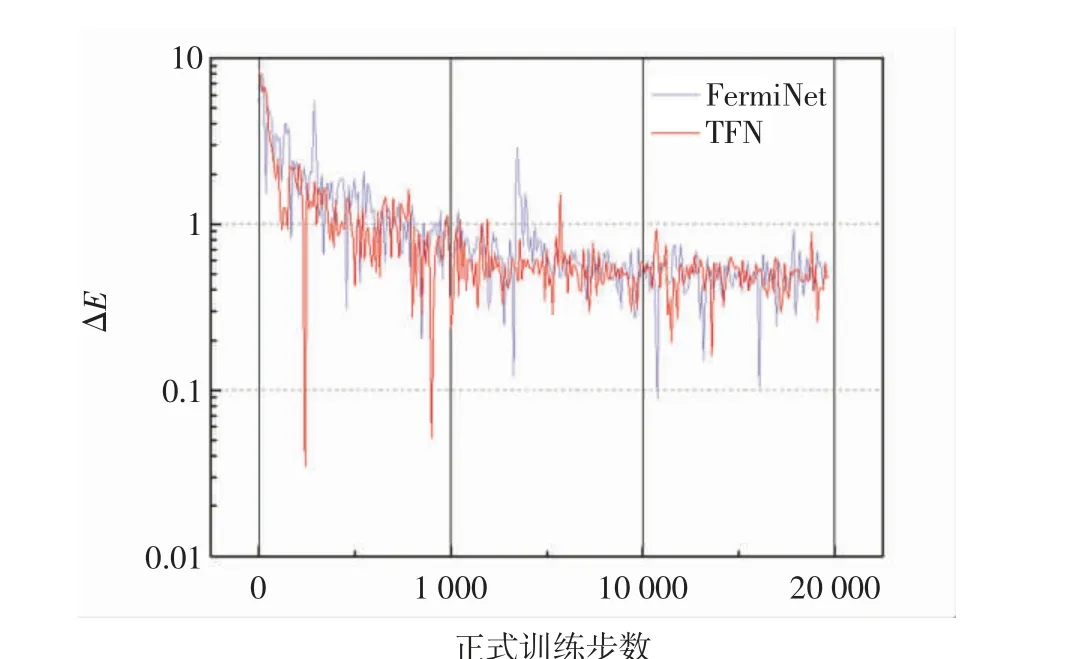
图9 TFN 与费米网络的优化过程Fig.9 Optimization progress of the TFN and FermiNet

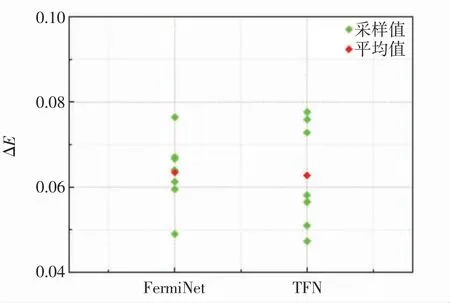
图10 基态能的采样均值对比Fig.10 Comparisons of sampling mean values of the ground-state energy

此外，费米网络在计算小分子时所得结果的精度已高于量子化学中的化学精度，但受限于计算资源，实际计算结果并未达到文献[13]中的精度.本研究所用资源是一张GTX 1650（3G）显卡和一张Titan xp（12G）显卡.此时，使用Transformer 结构后的TFN 达到等同费米网络的精度，其中间层使用的参数量却不足费米网络的2/3.在单电子流首层中TFN 使用了HT，但因为HT 只有一层，且只针对电子-原子核间距离的绝对值进行处理，其参数数量相对较小，对神经网络整体参数的量级影响不大，具体参数数量如表2 所示.此处，费米网络选用单电子流32 个隐藏单元，双电子流8 个隐藏单元.TFN 中HT、ST 和DT 的自注意力机制参数和线性连接单元数量分别选用（16，4）、（32，16）和（16，8）.

表2 TFN 与费米网络参数的对比Tab.2 Comparisons of parameters of the TFN and FermiNet

4 结论与展望

本研究采用包含自注意力机制的Transformer 结构替换网络中的线性连接结构，对费米网络进行了研究和改进，得到以下结论：

（1）研究了费米网络的结构并计算了引入不同自注意力机制的改进. 以小分子系统的基态能计算为例，对使用Transformer 结构后系统内部参数对神经网络优化体系基态能的影响进行测试，并给出参数选择的建议，结果表明自注意力机制参数带来的优化效果优于线性连接参数的效果.

（2）对比了TFN 和费米网络的计算结果.在小分子的计算中，TFN 使用了比费米网络更少的参数，但得到了与费米网络相同精度的结果，TFN 的单电子流参数数量约缩减为费米网络的60%，双电子流参数数量为费米网络的175%，总体参数量缩减约为费米网络的75%.上述结果说明TFN 对费米网络结构的改进是有效的.

此外，Transformer 结构的自注意力机制中存在一些中间变量需要存储，在经过权值共享沿电子数的维度拓展后，这些中间变量占用的显存会迅速膨胀.对此，在计算资源允许的条件下，可以采用DeepSpeed 提供的ZeRO-OffLoad 框架，将中间变量存储在内存中，降低显存压力，这使得Transformer 结构有可能被推广到较大系统中计算.

致谢 感谢中国人民大学卢仲毅教授建议的费米网络（FeimiNet）研究方向以及利用自注意力机制（self-attention）优化费米网络的研究思路.感谢中国人民大学贺荣强副教授的讨论和指导.感谢中国人民大学物理系提供的GPU 计算资源.