应变情况下CeO2 晶体电子结构的第一性原理研究

施慧芳，夏 卓，王艳萍，黄 珊，赵 辉

（天津师范大学物理与材料科学学院，天津 300387）

在过去几十年里，二氧化铈（CeO2）作为重要的稀土氧化物引起了人们的广泛关注.CeO2是一种具有高稳定性和无毒性等特性的n 型半导体，被广泛应用于三元汽车催化（three way catalyst system，TWC）[1]、固体氧化物燃料电池（solid oxide fuel cells，SOFCs）[2]以及传感器[3]等领域.CeO2在紫外光区（λ ＜400 nm）表现出良好的光催化性能[4]，且与TiO2类似，具有独特的Ce-4f态，表现出更高的光催化活性，这意味着CeO2有望成为一种高效的光催化材料.此外，CeO2具有带隙宽和介电常数相对较高等特点，不仅是催化[5]和光学涂层不可或缺的材料，也是稀磁半导体（diluted magnetic semiconductors，DMS）优良的基础材料[6].目前，研究人员对CeO2的结构和电子性质进行了大量研究，如Xiong 等[7]基于密度泛函理论对金刚石砧座中的同步辐射X 射线衍射进行分析，研究表明20 GPa 高压下，纳米CeO2由立方萤石型结构变为斜方α-氯化铅型结构.Patel 等[8]通过密度泛函理论研究了块状CeO2的结构以及单相和三相单层的电子性质，研究表明CeO2纳米结构具有多种电子性质且可通过应变进行调节.由于CeO2晶体结构中的八面体空隙未被氧原子完全填充，会形成氧空位缺陷，使得晶体内离子可以快速扩散.研究人员利用CeO2氧空位缺陷的这一特点，将其作为活化剂、稳定剂和分散剂等成分加入到催化剂中[9].目前，为增加氧空位数量，已有成熟技术将其他原子掺杂在CeO2中，改善材料的催化性能，扩展其应用领域.为了进一步优化CeO2的电子结构，可以通过施加应力、增加压强或外电场等手段来实现.通常材料的晶格结构会因应力作用而发生变化，相应的电子迁移率也会发生改变，同时声子和拉曼振动模式也会受其影响，从而实现对材料光学性质和热力学稳定性的调节，提高其应用的可靠性.

为了进一步认识应力对CeO2性能的影响，本研究基于密度泛函理论的第一性原理分析应力对CeO2晶体结构的影响，即通过拉伸和压缩技术研究CeO2电子结构的变化，并利用不同应力下的声子谱研究其结构的变化以及拉伸和压缩状态下CeO2的热力学稳定性.

1 计算方法和模型构建

本研究计算基于第一性原理，利用Materials Studio软件包中的CASTEP[10]（Cambridge sequential total energy package）完成.CASTEP 是基于密度泛函理论（density functional theory，DFT）的平面波赝势方法的量子力学程序. 采用基于平面波基组的模守恒赝势[11]（norm conserving pseudopotential）描述离子实和价电子间的相互作用势，选取O-2s22p4和Ce-4f15s25p65d16s2电子组态作为价电子，其他轨道电子视为芯电子进行计算.计算中选用广义梯度近似（generalized gradient approximation，GGA）[12]下的PBE[13]泛函描述电子间的交换相关能，根据Mokhorst-Pack 方法对k 点进行采样，平面波截止能为500 eV，不可约布里渊区的k 点取3×3×3.为了获得稳定结构，在进行各项计算前采用BFGS 方法对构建的模型进行几何优化.进行自洽计算时，原子总收敛能取1×10-6eV/atom，为了保证计算的精确性，各原子间的相互作用力不大于0.05 eV/nm.

CeO2属立方萤石结构晶体，其原子分布具有面心立方相，空间群为Fm3m（空间群号为225），CeO2晶体的原子坐标分别为Ce（0，0，0）和O（0.25，0.25，0.25），晶体结构如图1 所示.

图1 中铈原子和氧原子分别用绿色和红色小球表示，铈原子位于正中心，周围环绕8 个氧原子，每个氧原子又对应4 个铈原子.为了得到稳定的体系，对CeO2晶体进行结构优化计算.优化后CeO2的晶格参数为0.534 nm，与实验值0.541 nm[14]接近，误差为1.3%，计算结果与实验值符合较好.本研究构造了不同应变程度下的CeO2模型，并运用CASTEP 软件对CeO2晶体进行计算.在CeO2原胞的基础上，分别拉伸（压缩）了原胞晶格常数的2%、4%、6%和8%，得到新的CeO2模型.

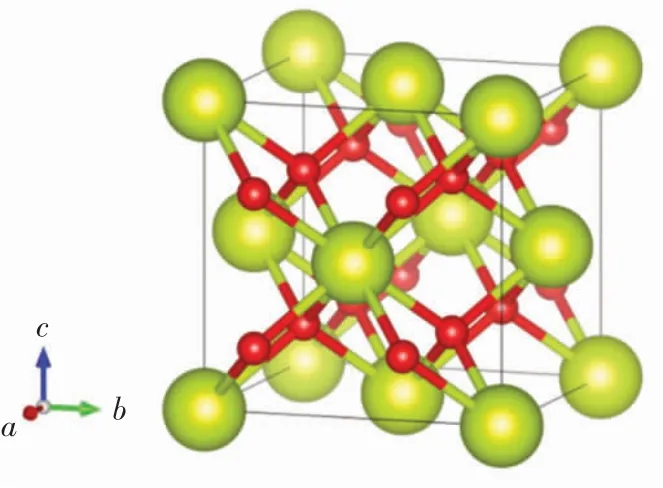
图1 CeO2 晶体结构Fig.1 Crystal structure of CeO2

2 结果与讨论

2.1 本征CeO2 的电子结构

采用广义梯度近似计算基态能级会低估带隙的大小，因此本研究在广义梯度近似下采用DFT+U 的技术[15]改进计算结果.当哈伯德参数U=7 eV 时，计算所得本征CeO2的带隙为2.966 eV（图2（a）），与实验值3.2 eV[16]和文献值2.94 eV[17]相近，可见改进算法（DFT+U）得到了满意的结果.由于Ce 4f 电子的强库仑相互作用，传统的基于广义梯度近似的DFT 无法描述Ce 4f 电子态的局域化，且低估了CeO2的带隙.因此，需要将哈伯德参数U 添加到GGA 函数（GGA+U）中，以校正Ce 4f 电子的相互作用.E=0 eV 处为费米能级，大于0 eV 的为导带，小于0 eV 的为价带.由图2（a）可知，CeO2晶体的费米能级未与较宽的能带相交，说明其导电性较弱.由图2（b）可以看出，价带和导带分别分布在-5～0 eV 和0～5 eV. 导带区2～4 eV 有1 个波峰，此波峰的出现主要来自Ce f 态电子的贡献，还有少量来自于O 的p 态电子的作用.在接近费米能级的价带区-4～0 eV 附近有几个连续峰，主要来自于Ce的d 态电子和O 的p 态电子的作用.总体来说，CeO2的价带最大值和导带最小值主要由Ce 的f 轨道和O的p 轨道贡献.

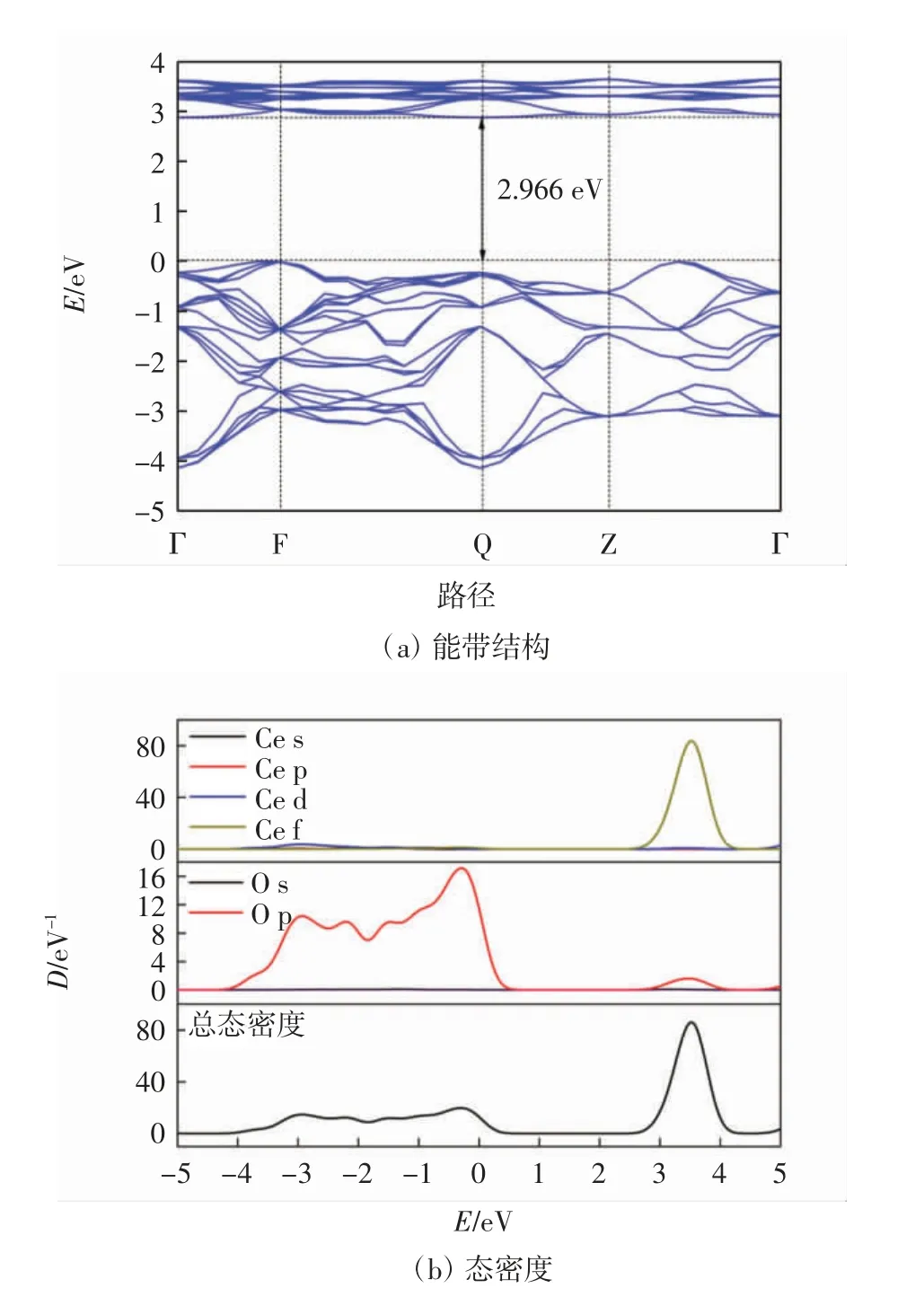
图2 CeO2 晶体的能带结构和态密度Fig.2 Energy band structure and densities of states of CeO2 crystal

2.2 应变对电子结构的影响

研究表明可以通过施加应力、构造掺杂或空位缺陷以及增加外电场等方法改变晶体带隙，由于半导体材料的带隙范围具有较高的弹性极限，可在较大范围内通过改变参数进行计算研究. 本研究通过对块状CeO2施加均匀的拉伸（2%～6%）和压缩（2%～6%）应变，且每个应变周期内的原子位置不被固定，分析不同应变（拉伸和压缩）对电子能带结构的影响，带隙值如图3 所示.

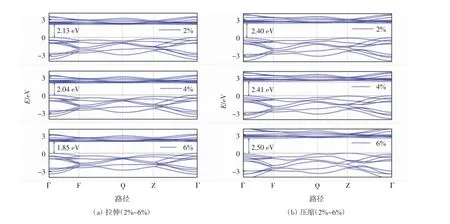
图3 CeO2 晶体在拉伸和压缩应变下的带隙图Fig.3 Band gap diagram of CeO2 under tensile and compressive strain

由图3 可以看出，块状CeO2晶体在2%～6%的拉伸应变范围内，带隙值逐渐减小；在-2%～-6%的压缩应变范围内，带隙值逐渐增大，最大的带隙值出现在6%的压缩应变下.

图4 为带隙的变化趋势.由图4 可知，当压缩应变在6%时，带隙呈间接带隙，块状CeO2晶体是一种间接带隙半导体.晶体层结构在不断裂的情况下所能承受的最大应力对应极限拉伸应变. 而在机械稳定性方面，通过计算应力-应变关系得到系统的极限拉伸应变[18-19]可知，块状CeO2晶体的拉伸应变范围大于压缩应变范围，即使施加12%应变的应力也不会断裂，即可以在很大的应力范围调节CeO2晶体的应变.

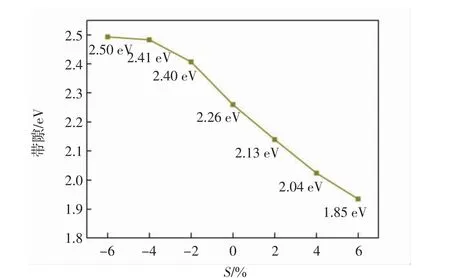
图4 CeO2 晶体在拉伸和压缩应变下的应变-带隙曲线Fig.4 Strain-band gap curve of CeO2 under tensile and compressive strain

2.3 拉曼光谱和声子色散

拉曼光谱为散射光谱[20]，是一种对分子结构进行精准、直接、无损测试的手段，被广泛应用于物理、纳米科学和材料科学等研究领域.拉曼光谱受热效应、应力效应和掺杂效应等外在因素影响较大[21]，下文将研究应力效应对CeO2拉曼光谱的影响. CeO2晶体的点群为Osh，空间群为Fm3m.依群论分析可知，在没有施加应力的情况下，本征CeO2晶体仅有1 个三重简并拉曼活性光学声子模和2 个红外活性声子模，且拉曼振动模只有F2g模式.本征CeO2在437 cm-1处有1个特征峰，此计算值与文献值439 cm-1[22]和文献值465 cm-1[23]的结果符合较好.

图5 给出了CeO2晶体在拉伸（2%～6%）和压缩（2%～6%）情况下的拉曼光谱图.

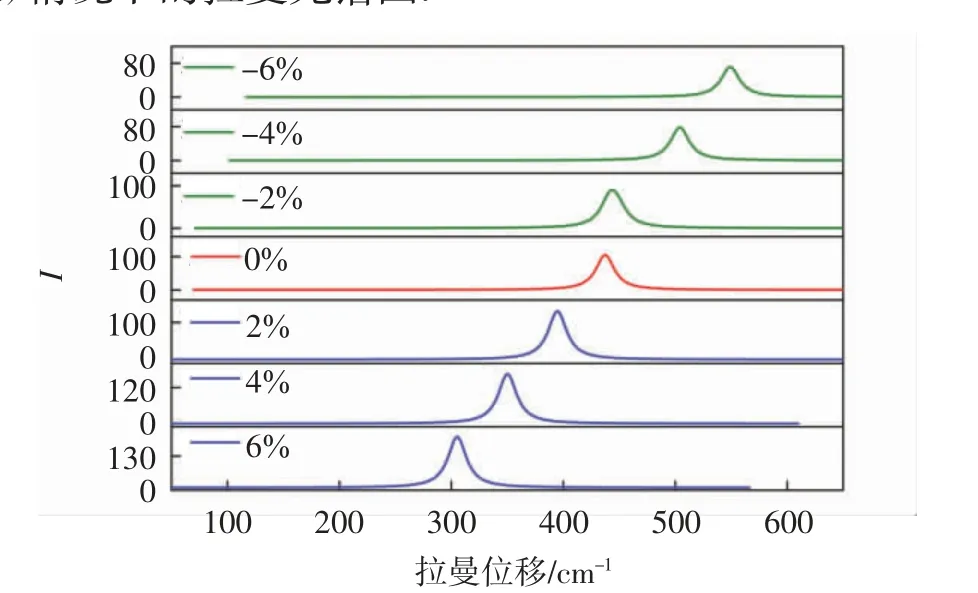
图5 CeO2 晶体在拉伸和压缩应变下的拉曼光谱Fig.5 Raman spectrum of CeO2 crystal under tensile and compressive strain

由图5 可以看出，CeO2晶体在2 种应变下的拉曼光谱均有较为规律的变化.拉伸情况下，CeO2晶体的键长发生变化，晶格常数也随之改变，由于拉曼峰的位置对晶格常数的变化非常敏感，所以拉曼峰值在拉伸情况下出现红移，拉伸程度越大，红移越大.相反在压缩情况下，随着压力的增加，原子间距减小，CeO2晶体的电子外壳发生重叠，一阶拉曼峰（F2g）向高频方向移动，这是由于应力的增大导致晶格常数降低，进而造成拉曼峰值发生蓝移，此现象也与实验结果[24]相对应.

声子色散谱是密度泛函理论中反映模型稳定性的重要手段[25].在声子谱中，如果声子色散曲线上存在频率为负，即色散频率小于0 的色散结构，就会出现相变的可能，因此这种结构是不稳定的[26].但若声学支在Γ 点附近有很小的虚频，则材料可以被当做稳定材料来对待.由此可知，若声子色散曲线值均为正值，则体系结构会非常稳定[27].CeO2作为重要的催化材料，稳定性和实验可能性一直是提高其催化能力非常重要的方向，即使在理论中能够稳定存在，若在实验上没有实现的可能性，则其实际意义也不大.为了考察应变情况下CeO2的热力学稳定性，需要分析其声子色散图和声子态密度图，结果如图6 所示.

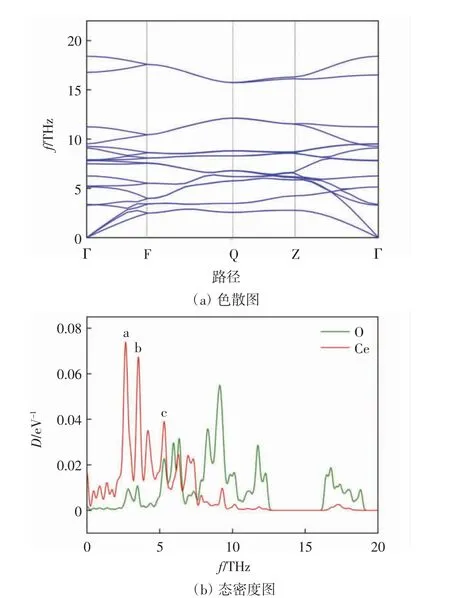
图6 CeO2 的声子色散图和声子态密度图Fig.6 Phonon dispersion diagram and phonon density of states diagram of CeO2

图6（a）为没有施加应力的CeO2晶体的本征声子色散曲线，其热力学稳定性可以通过观察声子色散曲线上的振动频率值来确定.由图6（a）可知，声子色散曲线的频率均为正值，表明处于本征状态的CeO2具有稳定的热力学结构.声子色散关系是频率与波矢的关系函数，而声子态密度是单位体积、单位频率间隔区间内的格波振动态数目.CeO2晶体的原胞只有3 个原子，包含3 个声学支和6 个光学支，且在声学支和光学支间没有出现明显的频率间隙.这是由于Ce 元素的相对原子质量远大于O 元素，O 原子在低频区域几乎没有振动模式出现，所以2 种元素分态密度的重叠区域不是很宽，造成处于低频区的声学支与处于相对高频区的光学支交叠. 依据CeO2的点群可以将CeO2在Γ 点的光学支表示为Γopt=T2g（R）+T1u（I），其中R 和I 分别表示拉曼活性模和红外活性模，T2g（R）和T1u（I）均为三重简并态.图6（b）为CeO2晶体的声子态密度图，由图6（b）可知，Ce 原子的振动贡献于低频率的声学支，而O 原子的振动贡献于高频率的光学支.Ce 原子的分态密度有a、b 和c 共3 个强度较高的峰，a 和b 分别对应频率为3.6 THz 和4.2 THz，与横向声学支的顶部相对应；c 对应频率为5.6 THz，可以将其归属于纵向声学支的顶部和光学支声子的底部.而纵向声学支和光学支之间存在的排斥作用会使声学支的色散关系走向非线性，进而影响CeO2晶体的热输运性质.

图7 为CeO2晶体在拉伸（2%～8%）和压缩（2%～8%）应变下的声子色散曲线.

图7 CeO2 晶体在拉伸（2%～8%）和压缩（2%～8%）应变下的声子图Fig.7 Phonon diagram of CeO2 crystal under compression（2%-8%）and tensile（2%-8%）strain

由图7 可知，对CeO2晶体施加2%～8%的拉伸应力时，声子频率没有出现负值，表明CeO2晶体结构具有良好的热力学稳定性.压缩6%和8%的情况下出现虚频（红色箭头标明），表示结构开始变得不稳定，且声子频率的变化愈发明显，说明晶格动力学中原子间的相互作用越来越强.压缩情况下，原子与原子间的距离变小，导致t 原子间的相互作用增强，造成频率增大.因此在实际应用中如果想要增强结构的稳定性不宜进行压缩处理.

3 结论

本研究基于密度泛函理论的第一性原理，从理论方面对CeO2晶体进行应变计算分析，研究结果表明：

（1）采用基于密度泛函理论的第一性原理系统研究了CeO2晶体材料的电子结构，得到CeO2能带带隙为2.966 eV，此结果与实验结果3.2 eV[16]基本相符.

（2）在块状CeO2晶体中，拉伸应变的带隙变化范围大于压缩应变的带隙变化范围，带隙在整个应变范围（-6%～6%）内呈减小趋势，且其压缩应变比拉伸应变更加敏感.

（3）CeO2晶体在拉伸和压缩情况下的拉曼光谱图均有较为规律的变化.拉伸情况下，拉曼峰值集体出现红移，拉伸的程度越大，红移的越多；压缩情况下，拉曼峰值发生蓝移.

（4）CeO2晶体在压缩6%后出现虚频，说明其结构开始变得不稳定，因此实际应用中要增强CeO2晶体结构的稳定性不宜进行压缩处理.