淤泥质土堤防边坡稳定性硬壳层作用效应分析

何利超，陆旭旭，赵新铭，姜 波，潘建伍

（1.中国电建市政集团山东工程有限公司，山东济南 250000；2.南京航空航天大学民航学院，江苏南京 211106)

引言

淤泥质土属于软土的一种，主要分布于海滨、湖滨、河流沿岸等地势比较低洼且常年积水的区域。淤泥质土具有含水量高、孔隙率高、压缩性高、抗剪强度低和承载力低的特点[1-3]，需要对这种软土进行处理才可用于工程施工。

采用大面积吹填砂进行围海造地时，会产生淤泥集中区。对大面积超厚淤泥层的地基处理，尤其是地表持力层的形成是一项亟待解决的工程难题[4]。另外，在沿海地区的道路建设中，经常遇到数米至数十米厚、抗剪强度低的淤泥层，其上覆盖有性质较好但厚度不大的地表硬壳层[5]。大面积硬壳层可在淤泥区形成一个有效的表面持力层，硬壳层的强度显著地高于淤泥层。通过硬壳层的应力扩散效应和连片整体效应，可以为上表面施工人员和设备提供稳定的支撑。由于硬壳层的应力扩散效应，可将土体表层荷载传递到更大的范围内，减小软弱土层所受应力。同时，硬壳层还具有壳体效应和封闭作用，使得下层淤泥土变形受到抑制，可有效提高土体结构的承载能力。曹海莹[6]分析了上覆硬壳层的软土路基动力响应问题，认为硬壳层的存在能够减小路基的残余变形。土体硬壳层广泛存在于岩土工程中，可将硬壳层相关理论推广到其他工程问题中，充分利用硬壳层的有利效应，克服硬壳层带来的不良特性。

本文针对青弋江分洪道工程侧平台淤泥质填土的不良性质，开展了多项室内试验，充分分析了该土体的物理力学特性。接着利用颗粒流PFC 建立了该堤防边坡的数值模型，采用细观强度折减法进行边坡的稳定性分析，得到了该边坡的安全系数。最后，根据现场分层填筑的施工特点，提出了边坡复合硬壳层的假设，讨论了硬壳层厚度、强度和层数等因素对边坡稳定性能的影响规律。边坡复合硬壳层的假设能够解释该堤防侧平台具有较高稳定性的原因，也可为现场施工提供理论参考。

1 工程概况

青弋江分洪道工程全长约47.28 km，堤防工程级别为Ⅲ级，设计防洪标准为20～40 年一遇，图1为该堤坝工程的堤身、侧平台示意图。该工程具有土方工程量大、地质条件复杂和土地资源稀缺的特点，芜湖地区符合规范的填筑土料总量有限，严重制约了工程施工进度。工程地质勘察报告显示，工程沿线分布大量淤泥质粉质壤土，呈软塑～流塑状，河道开挖料主要为该土料。施工单位利用该土料填筑堤防内外平台，以此弥补土方缺口。

图1 青弋江分洪道堤坝示意

2 土工试验

为了解青弋江沿线淤泥质土的物理力学性质，并为堤防边坡的稳定性分析提供参数，开展了淤泥质土物理力学特性的室内土工试验，包括界限含水率试验、颗粒分析、干密度、压实度、固结、击实、直接剪切（快剪、固结快剪、慢剪）、无侧限抗压强度试验、三轴压缩（UU、CU）等室内试验。采用ZJ 型应变控制式直剪仪（四联剪）进行直剪试验，对四个相同土样分别施加50 kPa，100 kPa，150 kPa，200 kPa 的垂直应力进行四联剪。三轴压缩试验采用TSZ-1 型全自动三轴仪，三轴试样尺寸为φ39.1 mm×80 mm，分别进行UU、CU 试验，如图2 所示。表1 为淤泥质土的部分力学参数，侧平台填土选用含水率高、淤泥质含量高的淤泥土，其c、φ值均处于较低的水平。

图2 淤泥质土室内土工试验

表1 青弋江淤泥质土物理力学参数

3 PFC 数值模型

3.1 细观力学参数标定试验

颗粒流PFC 在计算时无需定义宏观本构关系和对应的参数，而是采用局部接触来反映宏观问题，因此只需要定义颗粒和黏结接触的几何和细观力学参数。对于土体材料，采用点接触的接触粘结模型可得到更好的模拟效果[7,8]。而室内试验得到的宏观土工参数不能直接应用于软件计算，需要经过参数标定的过程来得到合适的细观参数[9]。

为了确定两种填土的细观力学参数，利用双轴压缩数值试验进行参数标定。PFC2D中有侧向约束的压缩试验称为双轴压缩试验，如图3 所示。其中上下墙（wall）以恒定的速度相向移动来模拟应变控制的加载效果，而左右墙（wall）通过伺服机制来维持固定的侧向压力来模拟围压。每个运算周期调用一次内部伺服函数来确定应力，并用数值伺服控制方式来调节侧向墙的速度，从而减少当前应力与目标应力之间的差距。整个加载过程中侧向围压基本保持不变，始终监测并记录轴向应力、应变等信息。

图3 PFC2D 双轴压缩试验

对于堤身填土和侧平台填土，分别进行了数次10、20、30、40 kPa 围压下的双轴压缩试验，不断调整数值试样的细观参数，直到数值试样的强度包络线与室内物理试验的结果基本一致，选取的c、φ值为表1 的快剪试验结果。表2 为最终得到的数值模型的细观力学参数，图4、图5 为不同围压下的应力-应变曲线和强度包络线，数值试样的c、φ值与室内试验结果基本一致，可认为数值试样能够反映两种填土的宏观力学性能。

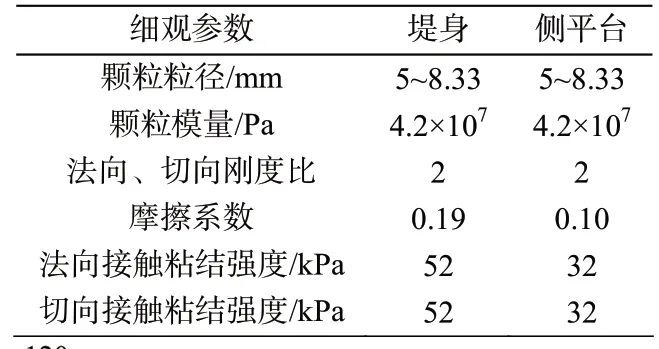
表2 数值试样细观力学参数

图4 堤身填土数值模型的力学特性

图5 侧平台填土数值模型的力学特性

3.2 青弋江提防边坡的PFC 模型

根据青弋江分洪道工程试验段堤坝的示意图（图1），建立了该堤坝的PFC 数值模型，如图6所示。为了降低计算量，只选取堤坝的右半部分进行计算。模型中颗粒尺寸沿用双轴压缩试验中的尺寸，即5～8.33 mm 随机分布，整个模型共30 839个颗粒。颗粒生成后，消除内部不平衡力，形成均质的颗粒集合体。接着为体系添加竖直向下的重力加速度，大小为9.8 m/s2，让模型在重力作用下平衡，最后为几种填土设置表2 中的细观力学参数。图7 为模型的力链示意图，力链的宽度对应着力的大小，可近似表示初始地应力场分布状况。

图6 青弋江堤防边坡的PFC 数值模型

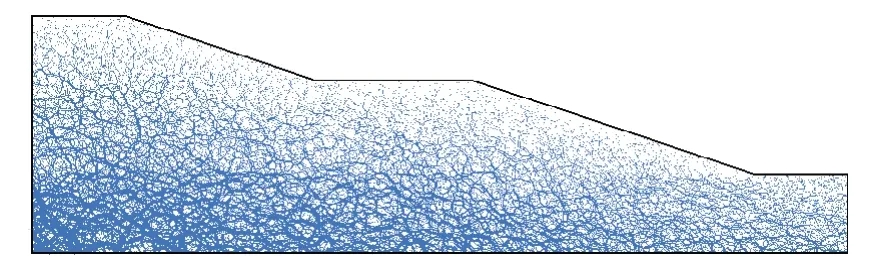
图7 青弋江堤防边坡数值模型的力链图

堤坝的侧平台填土土质较差，因此边坡失稳易发生于该部位。通过监测侧平台角点处的位移，可为边坡稳定性判断提供依据。角点位移是通过监测该点附近40 个颗粒的平均位移实现的。

4 堤防边坡的稳定性分析

4.1 边坡安全系数及位移

强度折减法是将土的强度参数除以折减系数Fr，然后进行稳定性分析，若边坡刚好失稳破坏，则当前的折减系数就等于土坡安全系数[10-12]。土坡的强度折减公式为：

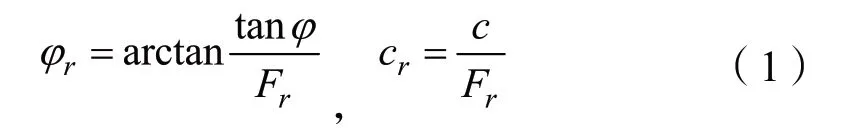
式中：φ、φr和c、cr为强度折减前后的粘聚力、内摩擦角；Fr为强度折减系数。

由于PFC 中定义的参数均为细观力学参数，因此上述宏观力学参数不能直接用于软件计算。根据PFC 模型中宏细观参数的特性，PFC 模型的摩擦系数影响土体材料的内摩擦角，模型的粘结强度影响土体材料的粘聚力，因此提出可用于颗粒流PFC 的强度折减公式：

式中：μ、μr为折减前后的摩擦系数；T、S和Tr、Sr为折减前后的法向、切向粘结强度。

计算结果表明，素土堤坝在重力作用下，经过了10 000 个时间步左右即达到了平衡状态，不再有颗粒的滑动。为了得到了土坡的安全系数，采用不断折减模型细观强度参数的强度折减法进行判断。若土体强度折减到某一程度时，土坡突然出现了滑动，认为此时的折减系数为土坡的安全系数。关于土坡稳定情况的评判，是通过监测点水平位移是否出现突变以及整个模型位移场的分布综合判定的。图9 为该堤坝在不同折减系数下，监测点水平位移随时间步的变化趋势。图10 为50 000 个时间步后，土坡在不同折减系数下的位移场分布。

图8 监测点水平位移变化趋势

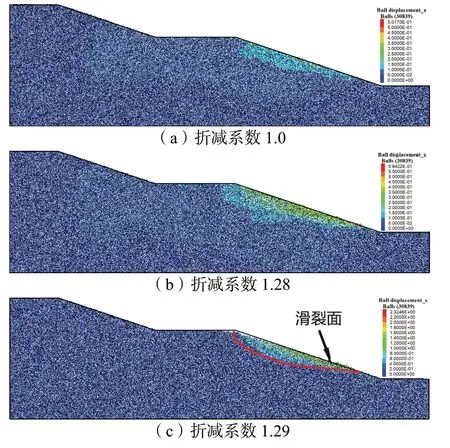
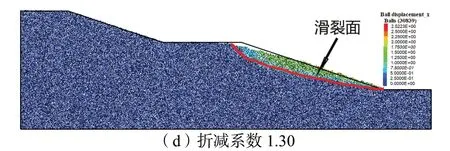
图9 不同折减系数下颗粒位移

在强度折减系数为1.0、1.20 和1.28 时，土坡监测点水平位移在10 000 时间步左右就保持不变，可认为这些土坡都是处于稳定状态。当强度折减系数为1.29时，监测点水平位移出现了突变，在10 000时间步仍然以较快的速度发展。当折减系数为1.30时，监测点运动的速度更大。观察土坡位移场分布图，在折减系数小于1.29 时，土坡发生了一定的变形，但此时其量值较小，并不能看到明显的滑动迹象。当折减系数为1.29 和1.30 时，侧平台填土上部颗粒位移显著高于其他位置位移，可以清晰的看到滑裂面。因此，土坡变形在折减系数为1.29 时达到了突变，可选取1.29 作为该土坡的安全系数。

4.2 复合硬壳层边坡稳定性分析

侧平台填筑土料为老堤堤基淤泥质土、圩内滩地或农田淤泥质土。填筑方法为：先采用合格粘性土填筑主堤身至平台高程，然后采用推土机或铲土机直接推送土料至侧平台填筑部位，边推送土料边碾压直至填筑高程，填筑完成后一般需要1～3 月后进行表层碾压、平整，图10 为工程施工现场。

图10 堤防边坡施工现场

工程现场采用分层填筑的施工方式，相邻填土层均有一定的时间间隔。在自然条件下，土坡表面会形成具有一定厚度的硬壳层。这种硬壳层类似于强夯法在地基表面形成的硬壳层，硬壳层的土质和厚度受碾压参数和晾晒时间等因素所控制，而硬壳层的层数受分层数所控制。硬壳层的强度、土质会明显优于素土，同时硬壳层具有应力扩散效应和封闭作用，对土坡的变形有着很好的限制作用[13-15]。因此，硬壳层的存在会加强土坡的稳定性，并对土坡的变形有一定的影响。

在数值模型中，主要考虑侧平台硬壳层的厚度、强度和层数对土坡稳定性和变形的影响，通过改变这三个变量来探究硬壳层对土坡稳定性的影响规律，土坡稳定性主要以安全系数来评估，而安全系数仍采用上文的细观强度折减法。

硬壳层强度会高于原淤泥质土，为了合理地设置PFC 模型的硬壳层参数，提出可用于离散元PFC模型的强度增强公式：

式中：Fn为土体强度增强系数；μn为增强后的摩擦系数；Tn、Sn为增强后的粘结法向、切向强度。

1）硬壳层厚度

为了分析硬壳层厚度对土坡稳定性的影响规律，设置硬壳层强度为原土强度的两倍（Fn=2），硬壳层的层数为三层，然后调整硬壳层厚度为0.3 m、0.6 m 和0.9 m，计算此时土坡变形情况和安全系数。图11 为不同硬壳层厚度下土坡的位移和安全系数变化。

图11 不同硬壳层厚度下边坡的稳定性

由计算结果可以看出：硬壳层的存在对于控制土坡变形有一定的促进作用，随着硬壳层厚度的增加，土坡的变形程度逐渐减小。同时，硬壳层可以增强土坡的稳定性，硬壳层的厚度越大，土坡的安全系数也在逐渐增加，土坡安全系数与硬壳层厚度几乎呈线性相关的关系。当折减土体强度后，淤泥土会有向下流动的趋势，但由于硬壳层的封闭作用，淤泥土就被封闭在硬壳层所形成的骨架中，最终土坡的变形和稳定性均有所改善。

2）硬壳层强度

硬壳层的强度与原土强度的比值同样会改变土坡的稳定性能，保持硬壳层厚度为0.3 m、层数为三层，分别调整Fn为1.5、2 和2.5。计算不同情况下土坡监测点水平位移和相应的安全系数，计算结果见图12。

图12 不同硬壳层强度下边坡的稳定性

由计算结果可看出：硬壳层强度增强后可有效地提高土坡安全系数，但其在控制土坡变形的作用有限，说明提高硬壳层强度的主要作用还在于维持土坡的稳定。

3）硬壳层层数

硬壳层的层数对应着填土分层填筑过程中的分层数，这一因素也会对土坡的稳定和变形有一定的影响。保持硬壳层的强度为素土的两倍（Fn=2），硬壳层厚度为0.3 m，改变硬壳层的层数为1、2 和3 层，计算此时土坡的安全系数和位移情况。图13即为不同硬壳层层数下土坡的位移和安全系数变化趋势。

图13 不同硬壳层层数下边坡的稳定性

硬壳层层数增加后，土坡的变形受到了限制，监测点的水平位移有所降低。同时，土坡的安全系数也在逐渐增加，土坡的稳定性得到了加强，硬壳层对土坡的稳定有很大的促进作用。

4.3 复合硬壳层对边坡坡度的控制作用

青弋江分洪道工程堤坝侧平台坡度比为1:3，根据计算结果可知该土坡是处于稳定状态的，安全系数为1.29。现在将坡度比改为1:2，进行稳定性计算分析。数值模型循环运行了50 000 步后，侧平台部分填土发生了严重的滑坡，图14 为侧平台局部放大图。根据数值计算结果，50 000 个时间步后，颗粒最大水平位移达到了9.2 m，监测点的平均水平位移为3.4 m。

图14 侧平台滑坡示意

下面将考虑土体硬壳层对该边坡的加固作用，在侧平台设置三层硬壳层，硬壳层厚度为0.5 m，硬壳层强度为原淤泥土强度的五倍。当侧平台拥有三层硬壳层后，边坡的稳定性得到了提高，由不稳定状态转变为稳定状态。同时边坡变形受到了限制，监测点最大水平位移仅为0.21 m。

对于青弋江分洪道工程堤坝，当侧平台拥有一定层数和厚度的硬壳层后，边坡的坡度可适当提高而边坡仍能保持稳定。青弋江分洪道工程堤坝全长约47.28 km，坡度的提高可以减少工程占地面积，具有很大的经济效益。

5 结语

本文针对青弋江堤防侧平台土料淤泥质含量较大、含水率较大的特性，开展了考虑复合硬壳层的堤防边坡稳定性分析，下面为主要的研究结论：

1）通过多组剪切试验和三轴压缩试验，对青弋江堤防工程填土的物理力学特性有了深入的了解，试验结果为后续数值试验提供了参数；

2）根据土体强度折减法的基本思想，提出了可用于PFC 模型中的强度折减法，通过对PFC 细观力学参数进行折减，得到了青弋江堤防边坡的安全系数，为边坡稳定性判定提供了依据；

3）根据侧平台分层填筑的特点，提出了边坡复合硬壳层的假设，复合硬壳层具有提高边坡稳定性、控制边坡变形的作用。硬壳层厚度、强度及层数均会对边坡稳定性有重要的影响；

4）利用硬壳层的加固作用，可在保证工程质量的前提下适当提高边坡的坡度，具有较大的工程和经济意义。