锚胫侧倾角对拖曳锚在砂土中的下潜性能大变形数值分析1)

于 龙 郭岩岩 李书兆

*(大连理工大学海岸和近海工程国家重点实验室，辽宁大连 116024)

†(中海油研究总院有限责任公司，北京 100028)

随着当今世界对于海底资源的开发由近浅海走向深远海，拖曳锚作为一种安装简便的锚固基础，得到了广泛的应用。拖曳锚锚胫与锚板形成一定角度，在锚链横拉作用下潜入海床。目前对于拖曳锚下潜性能的研究，多在不同程度简化锚几何形状的基础上建立数值模型或物理试验模型，聚焦锚的运动轨迹[1-4]、运动方向[5-7]、系缆点处的拖曳力[8-10]以及其拖曳角[1,6,10]等，这些因素都直接或间接地影响拖曳的嵌入性能。锚胫作为传力机构，起到控制拖曳角的作用，锚胫本身与土相互作用却不利于拖曳锚的下潜。对于拖曳锚锚胫影响的专门研究并不多，Kim[11]对锚胫的长度形状以及锚板锚胫连接点等做出研究，锚胫的厚度越薄越利于拖曳锚下潜，锚胫长度越短越有利于下潜。已有拖曳锚下潜性能研究中，多把锚胫简化为垂直于锚板上表面的规则薄板，例如矩形板、三角形板[11]，而实际工程中锚胫的形状以及摆放形式要相对复杂，锚胫表面以及锚板上表面存在一定的倾斜角度，如图1所示，其中锚胫侧倾角α是锚胫绕锚胫与锚板相交线为轴转动的角度，向对称轴线S方向为正，远离对称轴线S方向为负。对锚胫形状、角度（包括前倾角和侧倾角）等对拖曳锚下潜性能的影响开展研究，提出可能的优化方案并开展验证，具有一定学术价值工程应用意义。

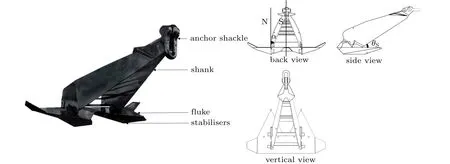
图1 拖曳锚示意图Fig.1 Schematic diagram of drag anchor

为了研究拖曳锚锚胫对安装下潜性能的影响，本文对传统拖曳锚MK5[12]进行建模，通过ABAQUS中耦合的欧拉-拉格朗日法模拟拖曳锚的安装过程，分析影响拖曳锚下潜性能的因素，提出改变锚胫侧向倾角的优化方案，并对优化效果进行分析。

1 耦合的欧拉-拉格朗日法

目前的有限元分析中，最常用的计算方法主要有两种：拉格朗日算法和欧拉算法，但是这两者均存在一定程度上的缺陷，前者的网格依附于材料之上，当材料发生移动时，易导致网格发生畸变进而造成模型计算不收敛，而后者则是网格固定材料可以自由流动，虽然克服了前者的网格畸变缺陷，但无法灵活追踪材料边界的变化，使得计算的精确度大大降低。

在这两者的基础上，Noh[13]最先提出耦合的欧拉-拉格朗日方法，集两者的优点于一体，之后由Benson等[14-15]在该概念的基础上进行完善开发并引用至ABAQUS有限元软件之中使用显示时间积分方法[16]。即在不需要迭代的基础上，根据前一个时间步的解得到下一步的结果，显示积分条件较为稳定。通过欧拉材料体积分数追踪计算过程中的材料流动，当网格中没有材料填充时，体积分数为0，当网格被材料完全充满时，体积分数为1。耦合的欧拉-拉格朗日方法材料可以自由流动且网格不会发生畸变，在大变形问题中得到了广泛应用[17-22]。

2 数值模型

2.1 数值模型建立

本文以规格为15 t的MK5拖曳锚模型为例开展研究，为提高模型的运算效率，采用无锚链牵引的拖曳锚运动分析模型，即拖曳锚的运动依靠施加于锚胫前端系缆点上的水平牵引速度，此速度根据Zhao等[23]的建议取为0.5 m/s。采用对称的锚-土作用模型。依据拖曳锚实际形状， 将MK5锚的锚板简化为不规则楔形体，忽略锚板上的稳定器；锚胫用不规则多边形薄板模拟，与锚板上表面法相方向成一定倾斜角度，忽略锚胫横撑。锚板和锚胫具体尺寸可见图2(a)，图中A=2.65 m，B= 3.904 m，C= 6.325 m，F=3.242 m，G= 0.585 m，拖曳锚材料杨氏模量E=2.1×1011Pa，泊松比取0.3。锚胫与锚板连接点位于锚板后中心点向前（G）0.585 m处，锚胫厚度依据资料取为60 mm，如图2所示，其中S为拖曳锚对称轴线（此时简化模型为一半的拖曳锚），N为锚板上表面法线。

海床土体采用砂土，具体尺寸可见图2(b)，即土体的长L= 80 m，宽W= 8 m，高D= 15.8 m。假定砂土不排水抗剪强度c= 2 kPa，泊松比µ=0.3，杨氏模量E= 15 MPa，砂土摩擦角φ= 20°，砂土浮重度γ′soil=8 kN/m3。其中土壤和锚之间的切向接触采用penalty（“罚”）接触方法，即近似于压力过度则闭合的行为。其中选取γa′nchor为29.267 kN/m3，依据《Anchor Manual》[12]中拖曳锚质量M为15 t以及对应规格拖曳锚尺寸，计算简化后的拖曳锚竖直模型体积Vanchor为3.82 m3，计算获得拖曳锚密度，重力加速度g取10 m/s2，水的容重γwater取10 kN/m3。

计算得到拖曳锚浮容重为29.267 kN/m3，与实际常用钢铁浮容重68 kN/m3相差较大，这是因为拖曳锚内部有中空。

2.2 锚胫角对拖曳锚运动特性影响

拖曳锚的锚胫前倾角对其运动特性具有一定影响，此时通过模拟锚胫前倾角θs分别为28°，30°，32°，34°，36°的拖曳锚模型的安装过程来研究锚胫前倾角对于拖曳锚下潜性能的影响，具体模型见图2。

图2 考虑锚胫的有限元模型Fig.2 Finite element model considering anchor shank

图3给出了不同前倾角下拖曳锚在水平横拉20A作用下的运动轨迹，其中A为对称锚模型宽度值。可以看出，拖曳锚前倾角对于拖曳锚的嵌入性能具有较大影响，其中最佳嵌入深度对应的最优前倾角处于32°～36°范围内。

根据图3(a)轨迹曲线可以发现，对于前倾角为36°的拖曳锚，其在下降至一定深度以后呈现向上运动趋势。而根据目前的现场经验[12,24]，采用较大前倾角时可能无法穿透中等至坚硬的黏土海床并沿海床滑动，而低锚角的锚可能容易穿透非常软的海床（例如正常固结的黏土），但终止于较浅的深度，具有较低的极限锚定能力。

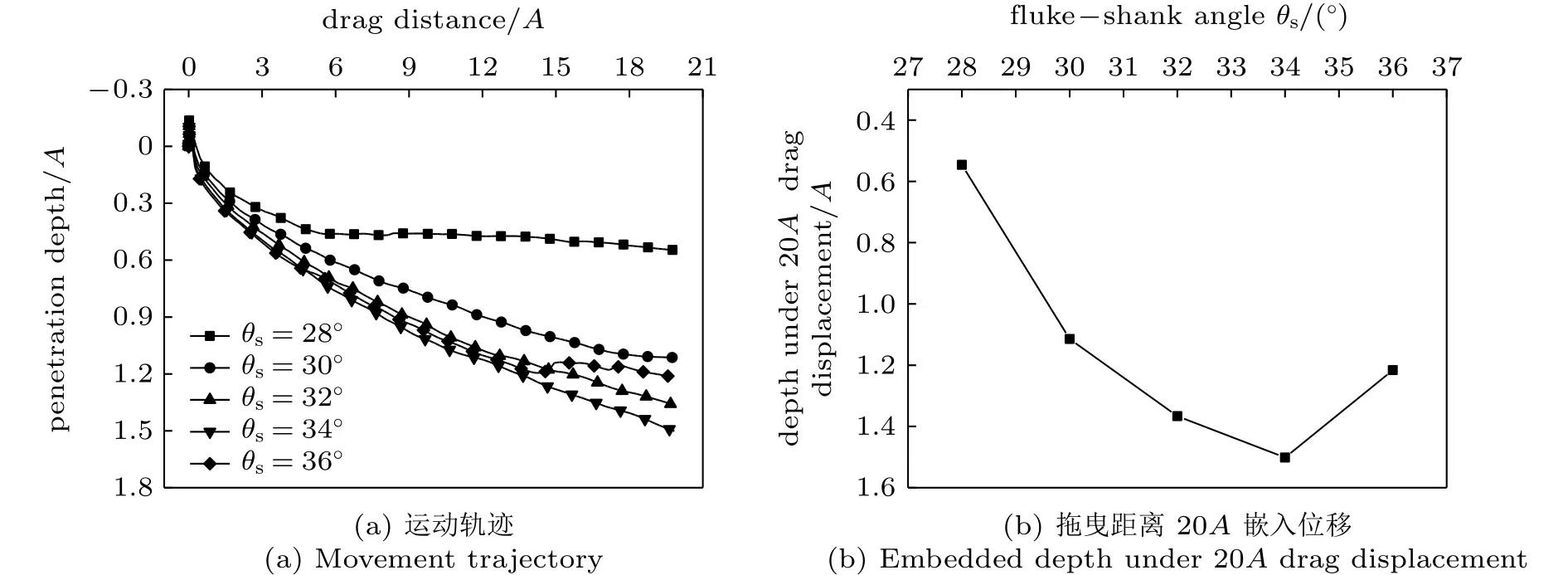
图3 锚胫角θs 对嵌入性能影响Fig.3 Influence of fluke-shank angle θs on embedded performance

2.3 锚胫侧倾角对其运动性能影响

锚胫不同侧向倾斜程度的拖曳锚模型如图4所示。

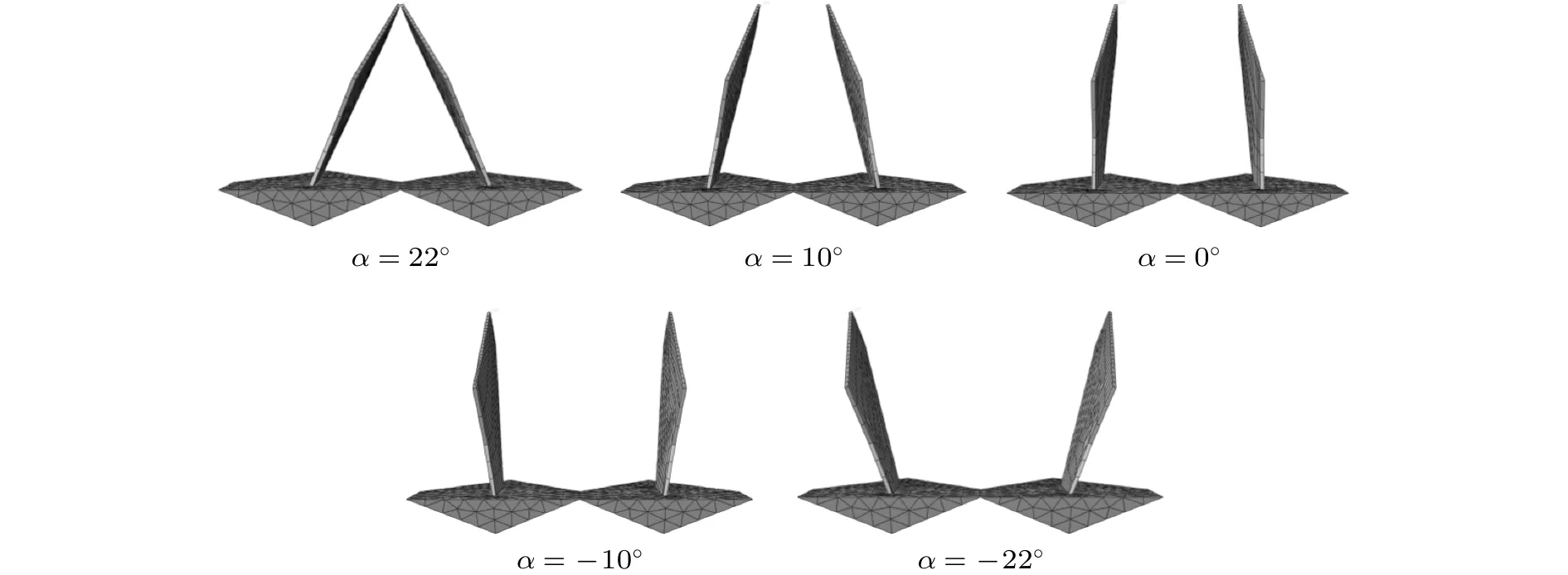
图4 不同锚胫侧倾角α模型（整体模型）Fig.4 Anchors with different lateral angle of shank α (overall model)

不同侧倾角的拖曳锚下潜运动轨迹如图5所示，可以看出，拖曳锚侧倾角对其下潜性能的影响十分显著，随着锚胫向外侧倾斜，其嵌入深度呈现明显增加的趋势，但是当倾斜至一定范围后停止增加，目前认为最优设计侧倾角在-10°～0°之间。在横拉20A的水平距离下，0° 侧倾角工况下潜3.271A，比原设计22° 侧倾角工况的1.301A增加了151%。这说明调整拖曳锚锚胫侧倾角对其的下潜性能有显著改善。

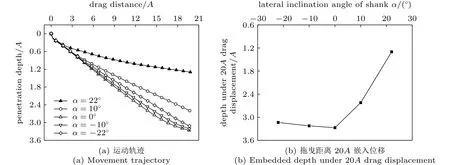
图5 锚胫侧倾角α 对嵌入性能影响Fig.5 Influence of α on embedded performance

3 土体重度和砂土摩擦角影响分析

拖曳锚的运动特性以及嵌入性能通常受多种因素影响，而拖曳锚的密度影响十分显著。为了研究拖曳锚浮容重以及土体内摩擦角φ的影响，分别以两者为变量设置了两组模型进行计算，其中拖曳锚浮密度分别取10 kN/m3，29.267 kN/m3，68 kN/m3，90 kN/m3，摩擦角则分别取20°，25°和 30°。

从图6(a)锚的嵌入轨迹可以看出，锚的密度对其嵌入性能有较大影响。随着锚的密度增大，其嵌入深度随之增加，与以往的工程经验和研究更为符合，同时从图7可以看出，土体摩擦角越大，其对应同等水平位置的嵌入深度越小，当摩擦角为30°时，拖曳锚出现下潜困难的现象，但通过增大拖曳锚的密度可以使拖曳锚顺利安装。因此，工程中出现相关无法下潜问题时，可以采用增加拖曳锚质量的方法辅助下潜。

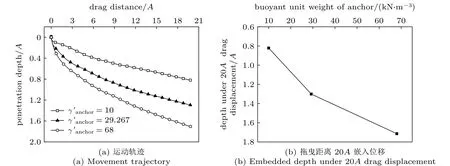
图6 拖曳锚浮容重对嵌入性能影响Fig.6 Influence of the buoyant unit weight of anchor on embedded performance

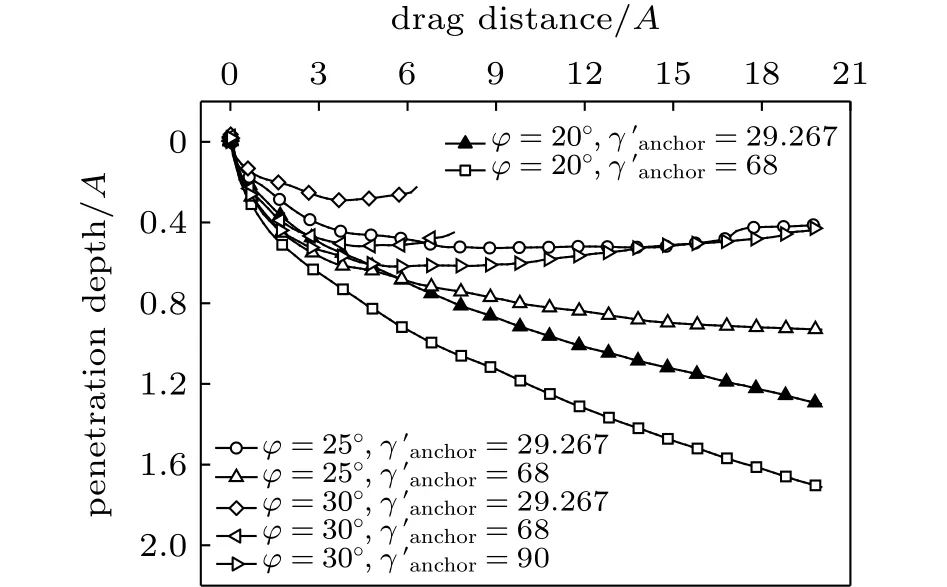
图7 拖曳锚摩擦角及浮重度对嵌入性能影响Fig.7 Influence of friction angle and buoyant unit weight on embedded performance

4 结语

提出了一种通过调整锚胫侧倾角来提高拖曳锚下潜性能的方法，以MK5拖曳锚为例，采用大变形有限元方法分析了锚胫前倾角、锚胫侧倾角、锚重和砂土内摩擦角等因素对其下潜性能的影响规律，得到如下结论。

（1）拖曳锚锚胫前倾角从28°增至36°时，拖曳锚下潜深度先增加后减小，最优的锚胫前倾角为 32°～36°。

（2）不同于传统内倾的锚胫，采用竖直锚胫或外倾锚胫时，拖曳锚的下潜深度明显增加。0°侧倾角工况下潜3.271A，比原设计22°侧倾角工况的1.301A增加了151%。说明调整拖曳锚锚胫侧倾角对其的下潜性能有明显改善。

（3）对拖曳锚密度以及摩擦角进行参数分析，验证随着密度的增大，拖曳锚下潜能力提高，随着摩擦角的增大，拖曳锚下潜能力降低，当拖曳锚在安装过程中无法顺利下潜时，可以通过增大锚的质量或者密度，来使其顺利下降完成工程任务。