考虑轴承故障高速列车齿轮传动系统振动响应分析

张阿中，刘建新，蔡久凤

（1.西南交通大学牵引动力国家重点实验室，成都 610031；2.西南交通大学机械工程学院，成都 610031）

齿轮传动系统作为铁路车辆转向架上的核心传动部件，其可靠性对列车运行平稳性和安全性有着直接的影响。目前，国内外学者对齿轮传动系统做了各方面的研究。Fernández 等[1]建立了球轴承支撑的考虑齿廓偏差的齿轮传动系统动力学模型，并通过实例验证了该动力学模型的有效性；Gu 等[2]建立了行星齿轮传动系统的动力学模型，模拟了齿轮出现偏心的故障情况，研究了齿轮偏心对行星齿轮传动系统动力学行为的影响；陈裴等[3]对行星齿轮传动系统进行动力学仿真，考虑太阳轮的断齿故障，研究了齿轮故障后系统的动力学响应。上述文献在建立齿轮传动系统动力学模型过程中，均没有考虑对齿轮传动系统中的轴承进行精细化建模，同样也缺少对轴承常见故障的模拟。

近年来，对故障轴承的仿真分析日益增多，刘永强等[4]建立了外圈故障的高速列车轴箱轴承动力学模型，对比分析了正常轴承和故障轴承的动力学行为；吴冬等[5]提出滚动轴承仿真建模方法，建立了铁路货车轴承的动力学模型，并验证了故障轴承模型的合理性；李长健等[6]建立了高速机车双列圆锥滚子轴承动力学模型，研究了内圈故障状态下轴承的动力学行为。这些文献模拟了轨道车辆轴承的常见故障，但只对轴承这一部件单独进行研究，并没有考虑轴承和其他部件的相互作用。

对于高速列车的齿轮传动系统，其输入轴上的轴承长期处于高速运行的状况，一旦出现故障，就可能会对整个传动系统甚至整辆车的稳定运行产生影响。因此，有必要考虑传动系统中轴承的常见故障，并对其产生的影响进行研究分析。本文在前人研究的基础上，对高速列车齿轮传动系统进行精细化建模，同时模拟轴承故障，建立考虑轴承故障的高速列车齿轮传动系统动力学模型，考虑故障轴承和其他部件的相互作用，研究输入轴上右侧圆柱滚子轴承出现剥离故障时系统的振动响应。

1 齿轮传动系统动力学模型

本文以国内某高速列车齿轮传动系统为研究对象，该系统由一对啮合的斜齿轮、两个圆柱滚子轴承NU-215、一个深沟球轴承QJ-214、两个圆锥滚子轴承EC-32994 组成，如图1 所示。主动齿轮和从动齿轮的齿数分别为35、85。各轴承的结构参数可根据其型号获得，如表1所示。

图1 高速列车齿轮传动系统简图

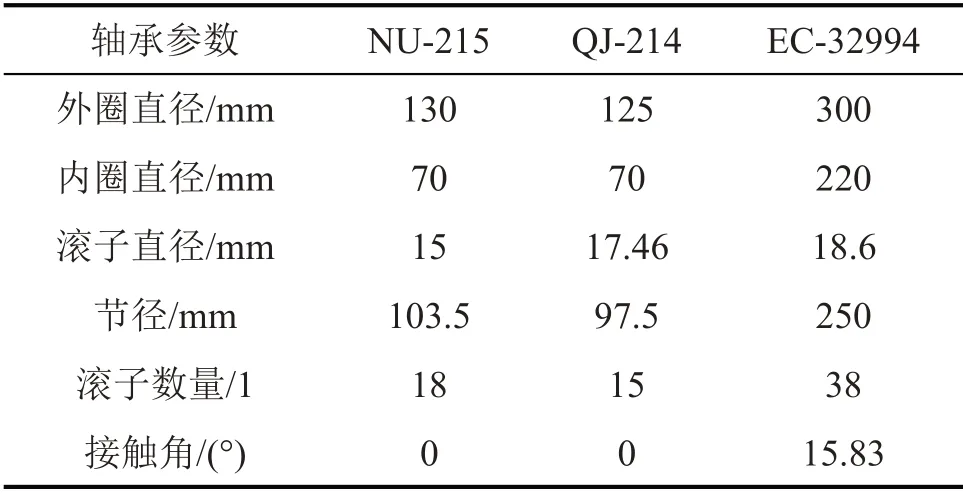
表1 高速列车齿轮传动系统中个轴承的结构参数

故障工况下，输入轴上右侧圆柱滚子轴承的内圈滚道上出现剥离故障，故障内圈是在正常内圈的基础上，切除截面为6 mm×1.5 mm的矩形凹槽来模拟，故障内圈的几何模型如图2（a）所示。

在SolidWorks 中创建好各零部件的几何模型后，导入到RecurDyn中进行传动系统动力学模型的创建，建模过程中，不考虑各部件的弹性变形。

1.1 接触关系设置

齿轮传动系统中需要设置接触的元件较多，滚动轴承需要设置滚子与内外圈、保持架之间的接触；主动齿轮和从动齿轮需在齿面上设置接触。Recur-Dyn 中计算法向接触力的方法为罚函数法，它将接触非线性问题转化为材料非线性问题。基于Hertz接触理论，接触过程中，法向接触力fn的计算公式为[7-8]：

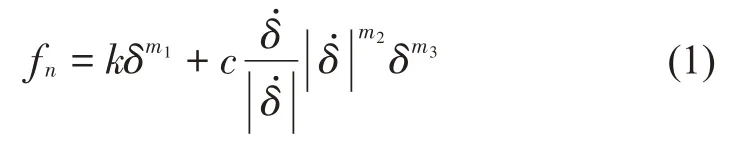
式中：k为接触刚度系数；c为阻尼系数；δ为接触穿透深度；为接触点的相对速度；m1、m2、m3分别为刚度指数、阻尼指数、凹痕指数。

1.2 约束设置

为模拟高速列车齿轮传动系统的实际运行状况，将所有轴承的外圈与大地固定，输入轴上轴承的内圈、主动齿轮与输入轴固定，输出轴上轴承的内圈、从动齿轮与输出轴固定，并在输入轴上添加驱动，角速度函数设置为STEP（TⅠME，0，0，0.2，440）。高速列车齿轮传动系统的动力学模型如图2（b）所示。

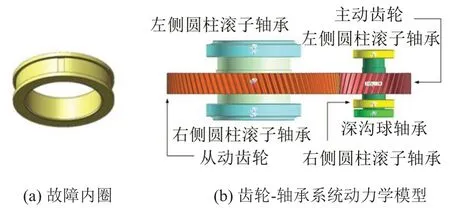
图2 齿轮传动系统动力学模型

2 模型验证

2.1 理论基础

滚动轴承正常运行时，假设滚子在内外圈滚道上的滚动为纯滚动，且轴承内外圈角速度保持不变，则保持架以及滚子的角速度[9]分别为：

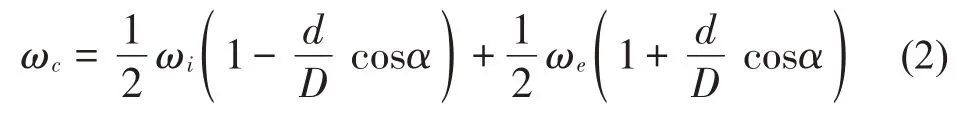
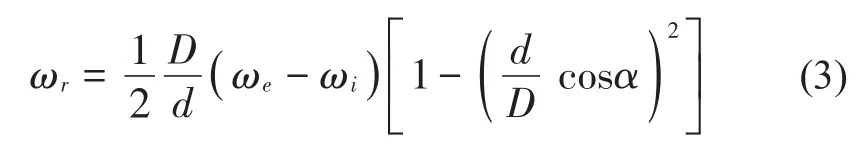
式中：ωc为保持架角速度，rad/s；ωr为滚子自转角速度，rad/s；ωi为内圈角速度，rad/s；ωe为外圈角速度，rad/s；d为滚子直径，mm；D为轴承节径，mm；α为接触角。

当滚动轴承中的零部件出现故障时，在轴承转动过程中，故障部位会与其他零件碰撞，从而产生一定频率的周期性激励，引起整个滚动轴承的振动。

滚动轴承内圈故障特征频率[10]计算公式为：

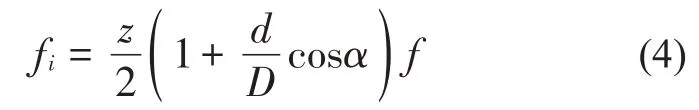
式中：fi为内圈故障特征频率，Hz；z为滚子个数；f为轴承内圈的转动频率，Hz。

齿轮的啮合频率的计算公式为：

式中：fm为齿轮啮合频率，Hz；fs为主动齿轮转频，Hz；zs为主动齿轮齿数。

2.2 模型验证

通过仿真可得到齿轮传动系统中各零部件的转速，将RecurDyn中得到的轴承保持架和滚子角速度仿真值与公式（2）～公式（3）计算出的理论值比较，如表2所示。

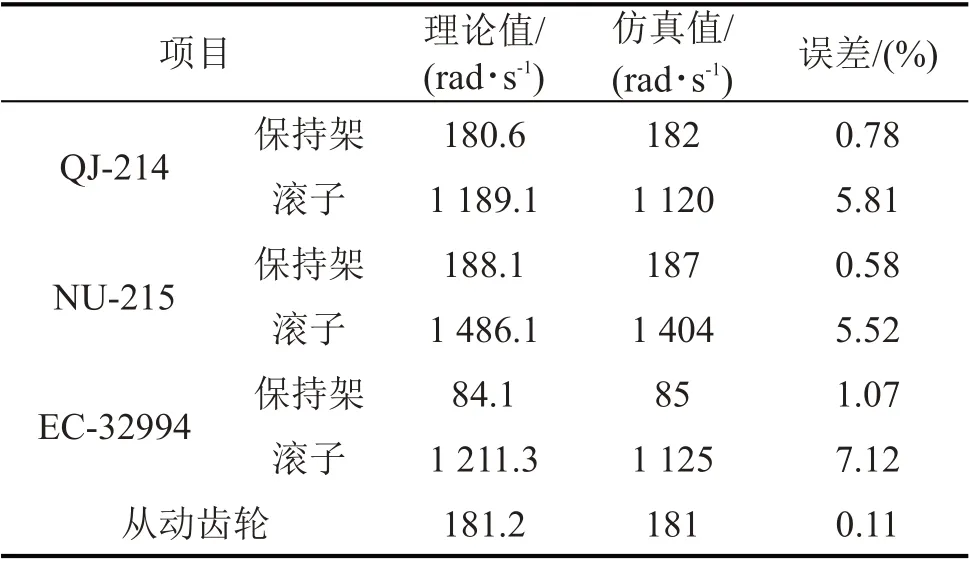
表2 理论结果与仿真结果比较

从表2中可以看出，输出轴上圆锥滚子轴承EC-32994的滚子角速度误差最大，考虑到轴承运转过程中滚子不可能一直做纯滚动，以及建模时对模型的简化，同时软件自身也存在一定的求解误差，且上述误差值均小于10%，处在合理范围内，可以验证齿轮传动系统动力学模型在运动学方面的合理性。

3 仿真计算

通过仿真分析，比较正常工况与故障工况下，齿轮传动系统中各零部件的振动响应，讨论轴承故障对系统的影响。

3.1 齿轮传动系统转速分析

在验证模型合理性的基础上，比较正常工况与故障工况下齿轮传动系统各零部件的角速度。从动齿轮的角速度如图3所示，从图中可以看出：正常工况下从动齿轮的角速度约为181 rad/s，与理论计算的结果很接近，且几乎没有波动；故障工况下从动齿轮的角速度有较大的波动，齿轮传动的稳定性降低。

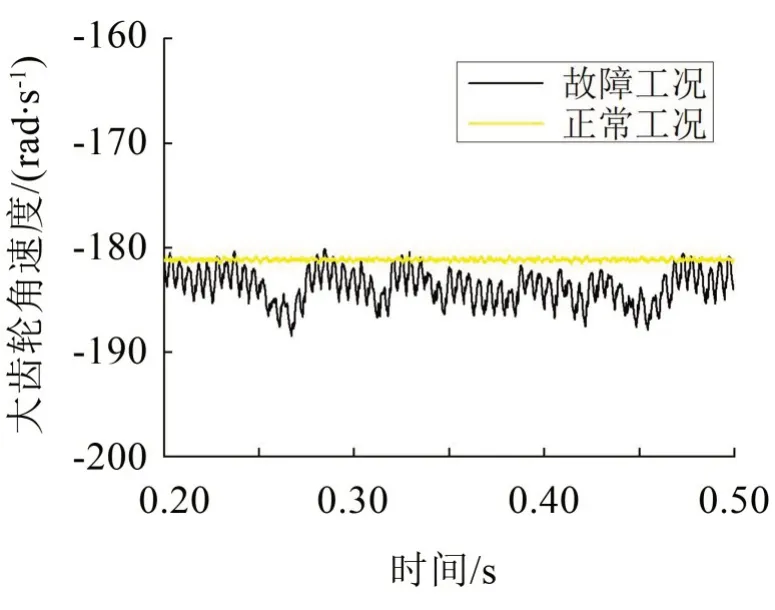
图3 从动齿轮角速度

输出轴上圆锥滚子轴承滚子的角速度如图4所示，从图中可以看出：故障工况下滚子的角速度比正常工况下有所增大，但并不明显，说明输入轴上的轴承出现故障对输出轴上的轴承影响较小。

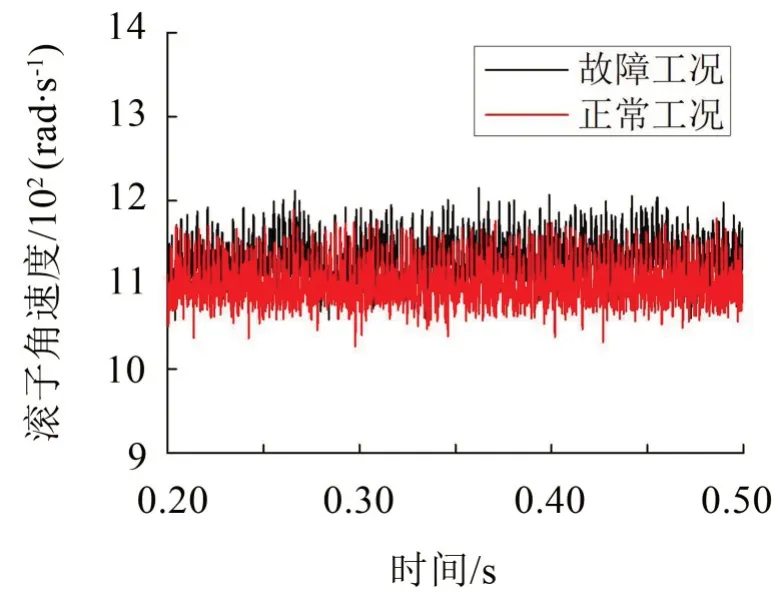
图4 圆锥滚子轴承滚子角速度

输入轴上右侧圆柱滚子轴承角速度如图5（a）所示，从图中可以看出：故障工况与正常工况下滚子角速度均值相差不大，但故障工况下滚子的角速度发生周期性突变，突变出现的时间间隔约为0.025 s，频率为40 Hz，为内圈转动频率70.03 Hz与保持架转动频率29.76 Hz（即滚子公转频率）之差，这是因为滚子公转方向与内圈转动方向相同，滚子无需公转一圈就会与内圈的故障部位发生碰撞，导致角速度突变。

输入轴上左侧圆柱滚子轴承滚子的角速度如图5（b）所示，从图中可以看出：故障工况与正常工况下滚子角速度的均值相差较小，但故障工况下，滚子角速度发生突变，且呈现一定的周期性。由此可见，输入轴上右侧圆柱滚子轴承故障不仅会使自身滚子的角速度突变，还会影响到同一轴上的其他轴承，使其角速度也发生突变。

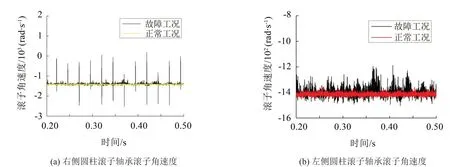
图5 圆柱滚子轴承滚子角速度

3.2 齿轮传动系统振动分析

由于主动齿轮、圆柱滚子轴承和深沟球轴承的内圈均固定在输入轴上，从动齿轮与圆锥滚子轴承内圈固定在输出轴上，对于多刚体系统而言，同一轴上各零件的振动加速度相同，因此只讨论主动齿轮和从动齿轮振动加速度的变化情况。

主动齿轮的振动加速度如图6（a）所示，经计算，正常工况下主动齿轮加速度的均方根值为873.03 m/s2，故障工况下为1 587.02 m/s2，由此可见，输入轴上的轴承出现故障后，会使主动齿轮的加速度明显增大。主动齿轮的振动加速度如图6（b）所示，经计算正常工况下主动齿轮加速度的均方根值为63.69 m/s2，故障工况下为232.29 m/s2，由此可见，输入轴上的轴承出现故障后，同样也会使从动齿轮的加速度增大。

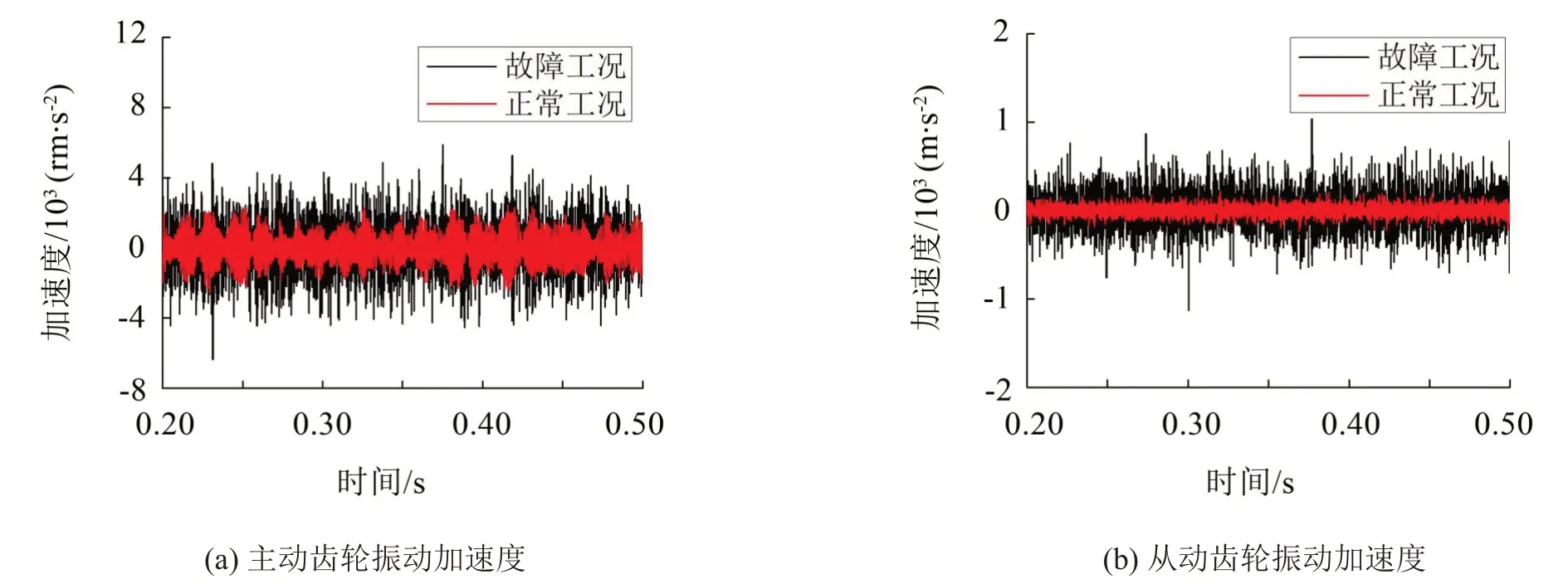
图6 齿轮振动加速度

根据公式（4）～公式（5），可求得圆柱滚子轴承内圈故障特征频率721 Hz，齿轮的啮合频率为2 451 Hz。

对故障工况下主动齿轮和从动齿轮的振动加速度进行谱分析，得到的加速度频谱图如图7（a）～图7（b）所示。可以发现：故障工况下，在图7（a）中，主动齿轮加速度频谱图在723.82 Hz处出现峰值，与理论计算的圆柱滚子轴承NU-215 内圈故障特征频率非常接近，在1 449.65 Hz 处也出现峰值，为内圈故障频率的2倍频，同时，在图中还可发现内圈故障频率的2 倍频与主动齿轮转频70.03 Hz 的调制频率1 519.63 Hz 和1 377.66 Hz；频谱图中1 421.65 Hz 处出现峰值，为内圈故障频率的2 倍频与圆柱滚子轴承保持架转频29.76 Hz 的调制频率；频谱图中2 451.40 Hz 处出现峰值，与理论计算得到的齿轮啮合频率很接近，在图中还可发现齿轮啮合频率与主动齿轮转频3倍频的调制频率2 241.45 Hz。

如图7（b）所示，故障工况下，从动齿轮的加速度频谱图中也出现圆柱滚子轴承内圈故障频率723.83Hz 及其2 倍频1 449.65 Hz，频谱图中还可发现齿轮啮合频率2 451.40 Hz。

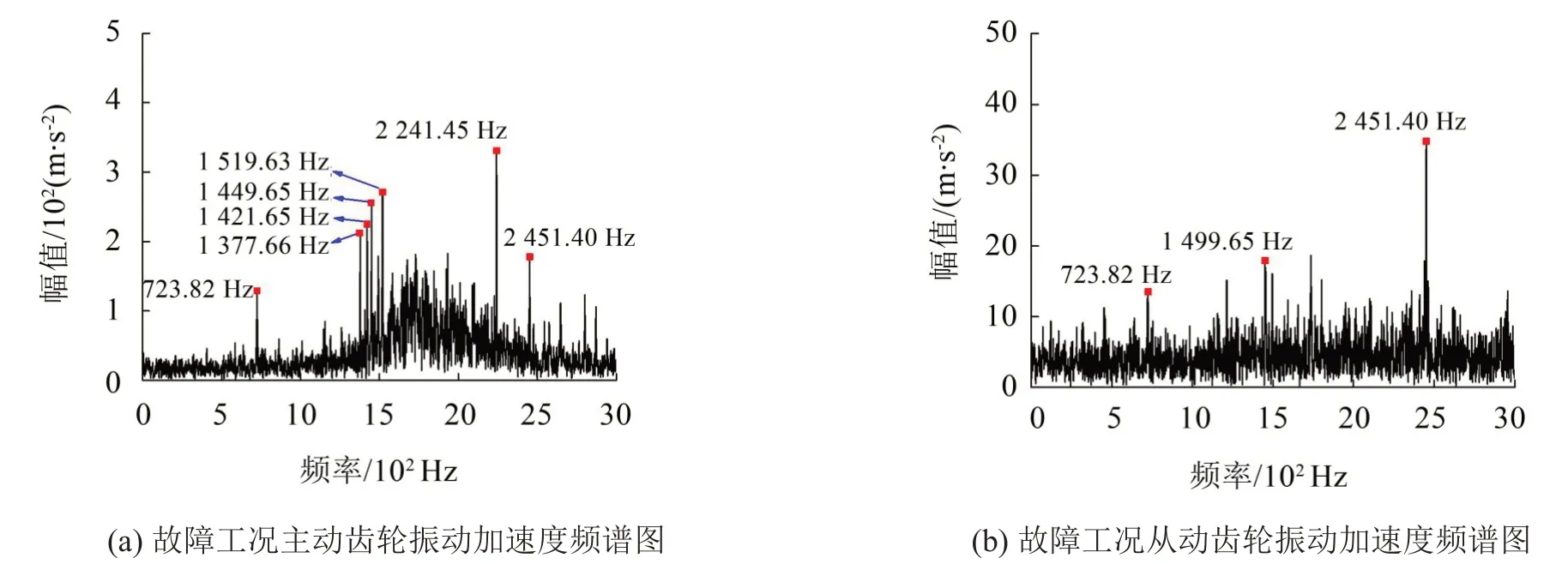
图7 齿轮加速度频谱图

通过上述分析，可以验证故障工况下齿轮传动系统动力学模型的合理性。

3.3 齿轮传动系统接触力分析

通过仿真分析得到主动齿轮和从动齿轮的接触力如图8所示。

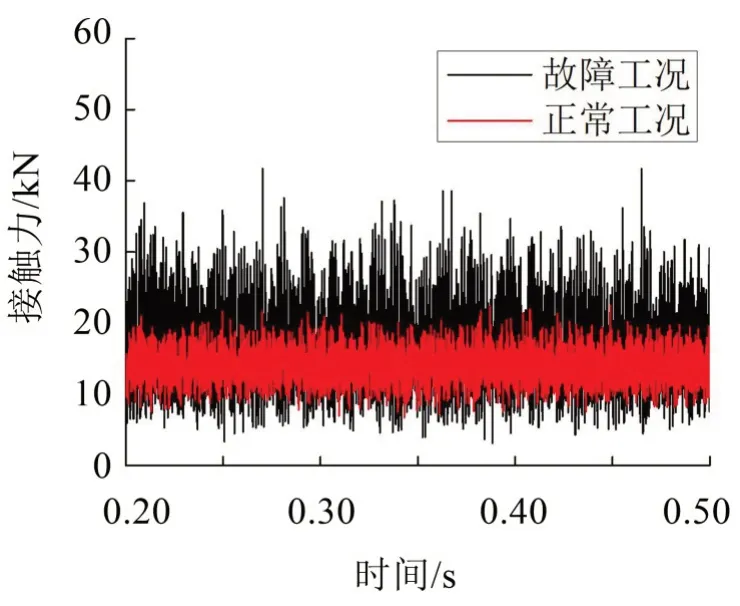
图8 齿轮齿面接触力

从图中可以看出，正常工况下，齿轮的接触力约为1 500 N，波动较小；故障工况下，齿轮的接触力急剧增大，由此可见，输入轴上右侧圆柱滚子轴承故障会导致齿轮齿面间的接触情况变得恶劣，进而可能缩短齿轮的使用寿命。

深沟球轴承滚子与内圈的接触力如图9 所示，从图中可以看出，故障工况下，接触力出现较大的波动，在某些时刻增大，在某些时刻又会减小到0，这是因为受到右侧圆柱滚子轴承剥离故障的影响，同一输入轴上深沟球轴承的滚子与内圈之间碰撞加剧，在某些时刻，接触力增大，同时由于轴承游隙的存在，滚子与内圈在某些时刻不产生接触，导致接触力为0，滚子与内圈瞬时脱离。

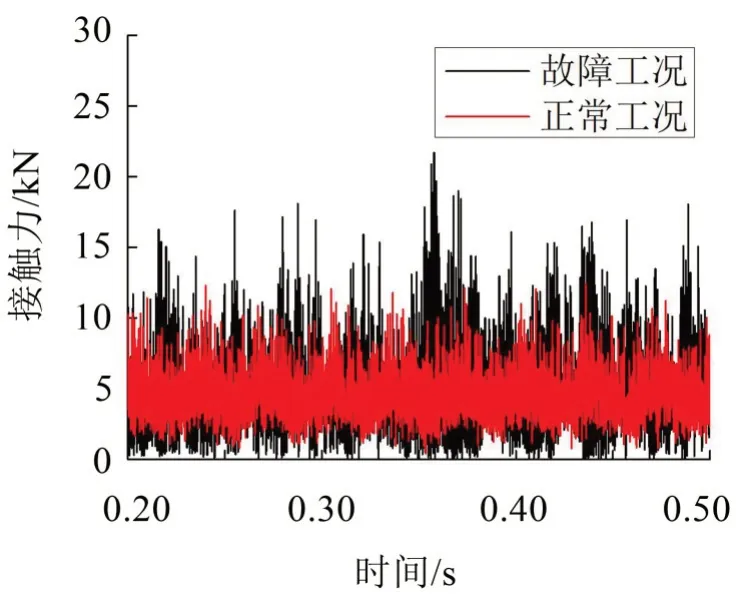
图9 深沟球轴承滚子与内圈接触力

右侧圆柱滚子轴承滚子与内圈接触力如图10（a）所示，从图中可以看出，与正常工况相比，故障工况下，滚子与内圈之间的接触力出现较大波动，在某些时刻增加，在某些时刻又会减小到0，说明滚子在经过内圈滚道上的剥离故障时，由于受到冲击，接触力会增大，但也因为剥离故障的存在，滚子与内圈在某些时刻不产生接触，导致接触力为0，滚子与内圈瞬时脱离。左侧圆柱滚子轴承滚子与内圈的接触力如图10（b）所示，从图中可以看出，故障工况下，滚子与内圈之间的接触力增大，说明左侧圆柱滚子轴承受到故障轴承的影响，滚子与内圈之间的碰撞加剧。

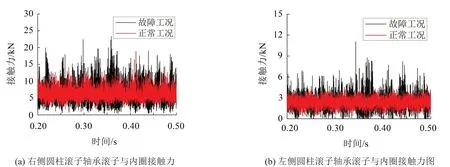
图10 圆柱滚子轴承滚子与内圈接触力

4 结语

为研究轴承出现故障后高速列车齿轮传动系统的振动响应，利用SolidWorks 和Recurdyn 建立了传动系统的动力学模型，在验证模型合理的基础上，对模型进行仿真分析，通过比较正常工况和故障工况下系统的动力学行为，得到以下结论：

（1）高速列车齿轮传动系统在运行过程中，受到输入轴上右侧圆柱滚子轴承内圈剥离故障的影响，从动齿轮的角速度变化剧烈，齿轮传动的稳定性降低；输入轴上各轴承滚子的角速度都会出现周期性突变，而输出轴上轴承受到的影响较小，滚子的角速度变化不明显。

（2）高速列车齿轮传动系统在运行过程中，受到输入轴上右侧圆柱滚子轴承内圈剥离故障的影响，输入轴上包括从动齿轮在内的所有零部件的振动加速度均明显增大，输出轴上所有零件的振动加速度也会增大。

（3）高速列车齿轮传动系统在运行过程中，故障轴承的滚子与内圈剥离故障处碰撞产生的冲击会传递到齿轮上，导致齿轮齿面间的接触力急剧增大，齿面接触情况恶劣，进而会缩短齿轮的使用寿命。

（4）高速列车齿轮传动系统在运行过程中，故障轴承的滚子与内圈故障处碰撞产生的冲击会使输入轴上轴承的滚子与内圈的接触力出现较大波动，在某些时刻会增大，但由于轴承游隙的存在，滚子与内圈在某些时刻会发生瞬时脱离，导致接触力减小到0，从而影响系统的稳定运行。

本文关于含故障轴承的齿轮传动系统动力学模型建模方法具有较高的准确性，该方法不仅仅可用于高速列车的齿轮传动系统，还适用于多数机械结构的齿轮传动系统，可以为齿轮传动系统故障诊断、预防提供参考数据。