基于混沌理论砂轮磨钝过程声发射信号试验研究

陈 芸，杨嘉睿，金容鑫，赵 淳，毛汉领

（广西大学机械工程学院，南宁 530004）

许多学者利用声发射技术来监测砂轮磨削过程，并对采集到的声发射信号进行分析，从而实现了对砂轮磨损状态的表征。Lopes 等[1]提出了用声发射间接监测砂轮表面完整性的方法，提出一种基于Kaiser窗口的算法来调整短时傅里叶变换参数以确保时频分辨率间的平衡，并利用该算法研究了氧化铝砂轮修整过程中的特征频率，在识别砂轮切削表面的地形条件方面取得了令人满意的结果。Dias等[2]通过对表面粗糙度Rz、圆柱度和圆度相关的声发射进行频谱监测。采用傅里叶变换和小波变换对磨削过程中的数据进行分析，提供了对信号的最佳理解，且在磨削过程中自动化生成智能信息。研究结果表明，声发射信号的谐波含量分析可以有效监测无心磨削过程。郭力等[3]通过实验研究了磨削声发射信号与磨削力和磨削温度间的内在联系，建立了工程陶瓷氧化锆与氧化铝磨削声发射信号与磨削力和磨削温度、磨削表面粗糙度关系式。结果证明，磨削声发射是实时工程陶瓷磨削过程检测的有效方法。丁宁等[4]建立了一种基于声发射信号的砂轮磨损检测模型，提出基于小波分解系数均方值统计分析的砂轮磨损状态特征提取方法，并且采用BP神经网络来识别砂轮磨损状态。龚子维[5]提出一种基于变分模态分解和概率神经网络的砂轮钝化声发射检测方法，搭建了声发射检测实验系统并对方法进行验证，成功实现了砂轮钝化状态的实时识别以及严重钝化的预警。郭力等[6]通过采集到的金刚石砂轮磨削陶瓷的声发射信号，运用小波分解系数的有效值、方差以及小波能谱系数作为金刚石砂轮磨损状态的特征值来反映其磨损状态，结合遗传算法支持向量机完成了对金刚石砂轮磨损状态的判别。钟利民等[7]对采集砂轮不同钝化状态下的声发射信号进行小波软阈值降噪后，将其划分为许多重叠的帧并组成数据集，利用分层Dirichlet 过程-隐半马尔科夫模型建立起数据集与砂轮不同钝化状态下的对应关系，最终实现了对砂轮钝化状态的识别。

混沌理论应用也很广泛。张栋梁等[8]利用混沌理论计算出刀具声发射信号的关联维数和最大Lyapunov指数，并与支持向量机相结合，实现了对刀具在不同磨损状态下的识别，并验证了此方法具有较高的识别率。关山等[9]通过采集刀具在不同磨损程度下的声发射信号，对其进行相空间重构，然后绘制出吸引子相图，并且求解出信号的关联维数，呈现出刀具的磨损状态与关联维数之间的对应关系。吴海勇等[10]结合混沌理论对单晶金刚石磨粒划擦Ta12W 的声发射信号进行分析，重构相空间后计算出了金刚石磨粒每个磨损阶段的关联维数，结果表明，单晶金刚石磨粒这种划擦磨损声发射信号具备混沌特性，且磨损程度与关联维数存在相应关系。虽然现如今有众多研究利用最大Lyapunov指数、关联维数和Kolmogorov 熵等混沌特征量来对不同机械设备的声发射信号进行分析，但是却鲜少有用来分析砂轮磨钝过程中的声发射信号。

本文通过采集到的砂轮磨钝过程中的声发射信号，运用混沌时间序列分析方法研究信号的混沌特征，分别计算不同时间段砂轮磨钝过程的声发射信号的最大Lyapunov 指数、关联维数和K熵，通过这三种混沌特征量研究揭示砂轮磨钝过程的动力学特性。

1 基本理论

1.1 相空间重构

C-C法可以同时求得延迟时间τ和延迟时间窗τω，继而由τω=（m-1）τ计算出嵌入维数m。该方法可以同时确定延迟时间和嵌入维数。具体步骤如下：

对于声发射时间序列{Xi}，i=1,2,…,N，将其分割成t个不相交的子序列，当N→∞时，每个子序列可定义为：

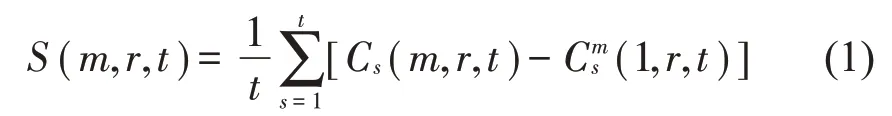
其中：（m=2,3,…），将最大半径ri和最小半径rj之间的差量定义为：

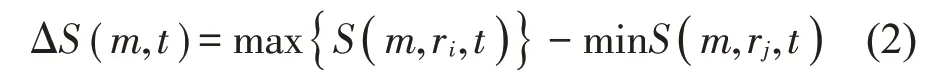
其中：i≠j。

经研究发现，当2 ≤m≤5，时，取得的参数较好。所以取m=2,3,4,5，，i等于1,2,3,4，（σ为时间序列的标准差），有：

则最佳延迟时间τ为（t）的第一个极小值，窗宽τω为Scor（t）的最小值，又由τω=（m-1）τ，可以计算出最佳嵌入维数m。

1.2 Lyapunov指数

Lyapunov 指数一般优先采用小数据量法计算，具体的计算步骤如下[11]：

对时间序列x（i）,i=1,2,3,…,N进行相空间重构，得到Xi，在相空间Xi中找寻每个点Xj的最近邻点，计算两点之间的欧式距离：

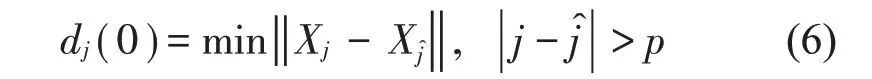
其中：p表示该时间序列的平均周期。

当每个Xi点经过i个时间步长后，距离就变为：

对每个i，计算出所有j的lndj（i）的平均值y（i）：

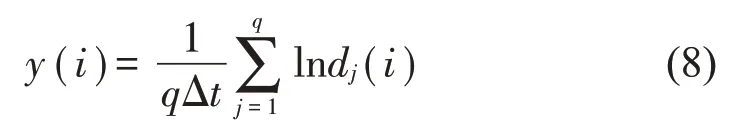
其中：q表示非零dj（i）的个数，Δt为演化时间步长增长量。

取i-y（i）的线性区域，基于最小二乘法原则，拟合一次回归曲线，该直线斜率即是所需的最大Lyapunov 指数。最大Lyapunov 指数大于0，那么系统具备混沌特性，其数值越大，系统的混沌程度也越大。

1.3 关联维数

关联维数计算原理如下[11]：

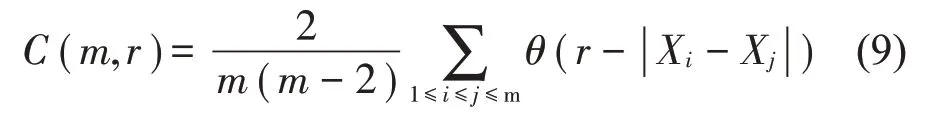
式中：θ（ ）为Heaviside 单位函数；r为邻域半径；|Xi-Xj|为两相点矢量Xi与Xj之间的距离。

1.4 K熵

Kolmogorov 熵（K熵）最大似然法计算步骤如下[12]：

不同轨道上的两个初始邻近点，它们从分开至间距大于r0所经历的时间满足指数分布：

其中：k表示K熵，b表示当初始间距比r0小的点初次超过r0时，在相空间上所经历的演化步数。在经b步演化后，两邻近点之间的距离大于r0的概率为：

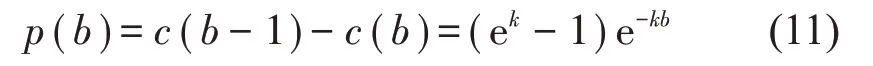
上面的概率密度函数满足下列条件：

有数据表明，翠香吸收钙的能力弱，对比其他品种，其植株内钙含量明显偏低。根据笔者随访，能够及时、科学补钙的翠香园，黑头病发生率极低。田间试验表明，氯化钙叶面喷雾浓度0.2%是安全有效的。有的钙安全稀释浓度只有万分之几，达不到有效补钙效果。建议喷雾防治病虫时加入钙肥。土壤施钙可能有钙元素被固定的问题，具体效果还需进一步试验。

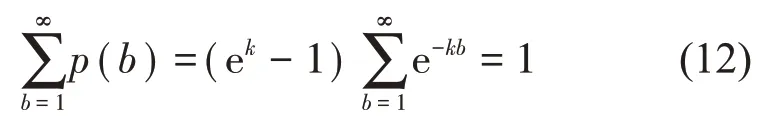
在相空间中随机抽取M对不相关的点，得到b1,b2,…,bM与k的联合概率：

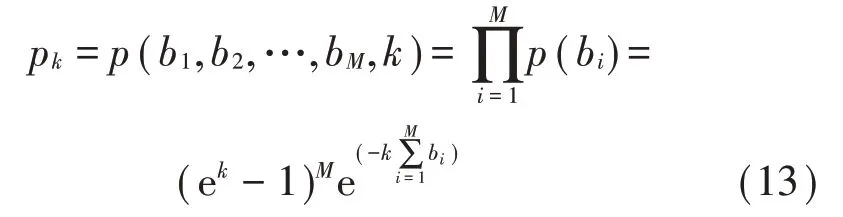
用式（13）可求得K熵的最大似然估计值为：

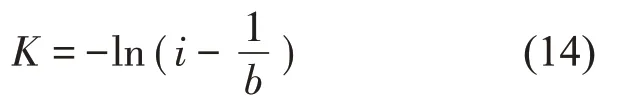
若K=0，表示系统做规则运动；若K→∞，表示系统做随机运动；若K＞0，表示系统做混沌运动，并且K的值越大，系统的混沌程度就越严重。

2 磨钝过程AE 信号混沌特性分析方法

基于混沌理论的砂轮磨钝过程的声发射信号的特性分析方法的具体步骤安排如下：

（1）混沌性检验：计算砂轮磨钝声发射信号的最大Lyapunov 指数，验证是否具有混沌性；

（2）相空间重构：采用C-C法同时求取最佳延迟时间τ和嵌入维数m；

（3）计算重构信号的混沌特征参数：采用小数据量法计算信号的最大Lyapunov 指数，采用G-P算法计算信号的关联维数，采用最大似然估计法计算信号的K熵。

（4）混沌特性分析：分析三种参数与砂轮磨钝不同磨损阶段之间对应关系。

3 实验装置与方案设计

试验使用的卧轴平面磨床的型号为M7150×1200/BZD，所用声发射检测设备是美国物理声学公司PAC生产的PCⅠ-2型双通道声发射测试系统。磨削工件材料为45 号钢，尺寸150 mm×60 mm×100 mm，声发射传感器型号为NANO-30，频率范围125 kHz～750 kHz。

实验装置如图1 所示，实验采用陶瓷结合剂白刚玉砂轮，尺寸（外径×厚度×孔径）400 mm×40 mm×127 mm，粒度为60#，硬度为中2，组织号为5，允许的最高线速度为35 m/s，实验中工作台速度不变，砂轮的转速固定为1 450 r/min，即砂轮线速度固定为30.4 m/s。在工件150 mm×60 mm 的平面内进行磨削。

图1 实验装置

试验布置如图2 所示，实验数据采样频率为1 MHz，声发射信号的采集门槛值设为40 dB，前置放大器增益为60 dB。

图2 砂轮磨钝过程声发射数据采集布置图

磨削实验过程中加工材料、砂轮型号、砂轮线速度以及工作台速度都固定不变，选择试验的磨削深度分别设为0.02 mm、0.03 mm、0.04 mm、0.05 mm、0.06 mm、0.07 mm，根据磨削深度的不同依次进行实验，直至砂轮磨钝，记录好数据。不同的磨削深度都重复进行三次实验。

4 实验数据分析

4.1 砂轮磨钝过程中声发射信号相空间重构

利用C-C法计算降噪后磨削深度为0.05 mm 时砂轮初期磨损阶段、稳定磨损阶段以及严重磨损阶段的声发射信号，计算结果如图3所示。

图3 砂轮不同磨损阶段的C-C法计算结果

如图3 所示C-C法计算得各磨损阶段的延迟时间τ和嵌入维数m。由图3（a）至图3（c）可以得到砂轮不同磨损阶段的延迟时间和嵌入维数分别为：τa=4，ma=19；τb=2，mb=34；τc=2，mc=33。同样地，也能由此计算其他声发射时间序列的最佳延迟时间τ和嵌入维数m。 之后再进行相空间重构恢复混沌特征轨迹。

4.2 最大Lyapunov 指数分析

如图4所示为磨削深度为0.05 mm时，砂轮磨钝过程中三个磨损阶段的声发射信号，利用小数据量法求出它们的最大Lyapunov 指数。以图4中红线部分的斜率为不同磨损阶段的最大Lyapunov 指数。

图4 砂轮稳定磨损阶段的最大Lyapunov指数

以实验1 为例，选取砂轮磨钝过程中的65 个时间段，分别在每个时间段中取6组数据，利用小数据量法计算这6 组数据的最大Lyapunov 指数，求出平均值，所得平均值就为各磨损阶段的最大Lyapunov指数，如表1 所示，砂轮各个磨损阶段的最大Lyapunov 指数都大于0，说明其不同磨损阶段的声发射信号具备混沌特性。且不同磨损阶段的值也不同，砂轮磨损程度越严重，对应的最大Lyapunov 指数越大。

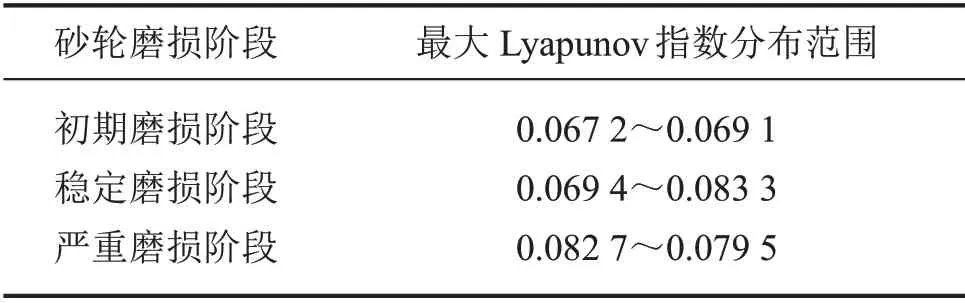
表1 砂轮磨损阶段与最大Lyapunov指数对应关系

同样地，如图5 所示，计算实验2 和实验3 砂轮磨钝过程中各时间段的最大Lyapunov指数，并将所得结果绘制在同一张图中。采用此方法得到磨削深度为0.02 mm、0.03 mm、0.04 mm、0.05 mm、0.06 mm和0.07 mm 时，砂轮磨钝过程各时间段的最大Lyapunov 指数变化趋势，以0.03 mm、0.05 mm、0.07 mm为例。

图5 不同磨削深度下的最大Lyapunov指数变化趋势

由图5 可知，在不同磨削深度下的砂轮初期和稳定磨损阶段的最大Lyapunov指数都不断增加，说明这两个阶段的混沌特性不断增强；到了砂轮严重磨损阶段，最大Lyapunov指数都呈现下降趋势。通过比较不同磨削深度下的最大Lyapunov指数，可以发现磨削深度的变化对最大Lyapunov 指数的影响很小。

4.3 关联维数分析

如图6所示，利用G-P算法计算关联维数时，以砂轮稳定磨损阶段的声发射信号为例，画出其lnC～lnr双对数曲线图。如图7所示，再做出关联维数随嵌入维数变化的曲线图，由图7可知，关联维数会随着嵌入维数m的增加而增大，当嵌入维数m=12时，关联维数已趋于稳定，此时砂轮稳定磨损阶段的声发射时间序列的关联维数m=5.219 1。

图6 砂轮稳定磨损阶段G-P 算法计算结果

图7 砂轮稳定磨损阶段关联维数m随嵌入维数变化图

依此可以计算出砂轮各个磨损阶段的关联维数。以实验1为例，取砂轮磨钝过程的65个时间段，分别在每个时间段中取6 组数据，用G-P算法计算这6 组数据的关联维数平均值，所得平均值就是各时间段的关联维数。同样地，如图8所示，计算实验2 和实验3的关联维数。采用此方法可得到不同磨削深度时，砂轮磨钝过程中各个时间段的关联维数。

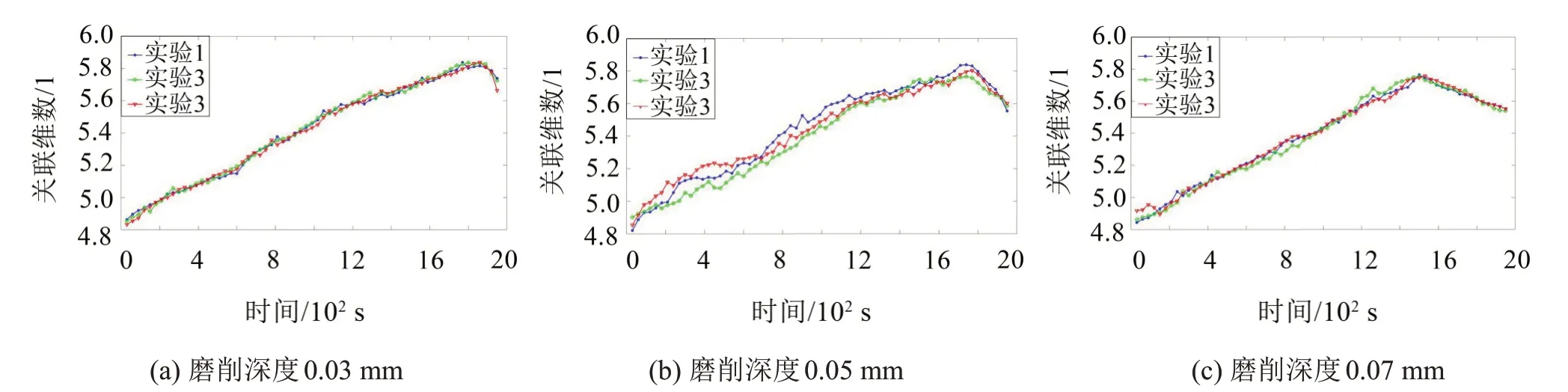
图8 不同磨削深度下的关联维数变化趋势

从图8 可以看出，在不同磨削深度下的砂轮初期磨损阶段和稳定磨损阶段的关联维数都不断增大，说明这两个阶段的混沌特性不断增强；到了砂轮严重磨损阶段，关联维数都呈现下降趋势。

4.4 K熵分析

如图9 所示，以砂轮稳定磨损阶段的声发射信号为例，采用最大似然算法计算砂轮磨钝过程中声发射时间序列的K熵值。由图9可知，K熵值随着嵌入维数m的增大而减小，当嵌入维数m＞10时，K熵值基本趋于稳定，此时砂轮稳定磨损阶段的声发射时间序列的K熵值为1.002 3。

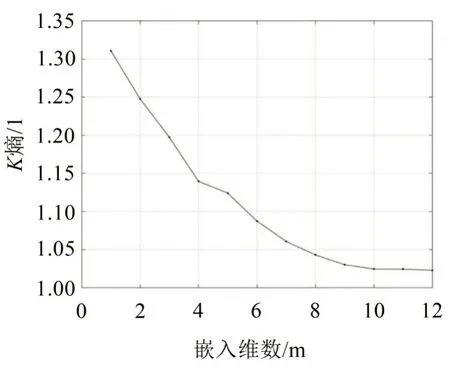
图9 砂轮稳定磨损阶段K熵随m变化图

同样地，可以计算出砂轮各个磨损阶段的声发射时间序列的K熵。以实验1 为例，选取砂轮磨钝过程的65 个时间段，分别在每个时间段中取6 组数据，用最大似然算法计算这6组数据的K熵值，所得平均值就是各时间段的K熵。同样地，如图10 所示，计算实验2 和实验3 磨钝过程中各时间段的K熵，以下仅列出0.03 mm、0.05 mm、0.07 mm 时的趋势图。

从图10可以看出，砂轮在不同磨损阶段的声发射信号的K熵大于0，进一步说明了砂轮磨钝过程各阶段的声发射信号均存在混沌特性；在不同磨削深度下的砂轮初期磨损阶段和稳定磨损阶段的K熵值都不断增大，说明这两个阶段的混沌特性不断增强，复杂程度增加；在严重磨损阶段，K熵值都呈现出下降趋势。

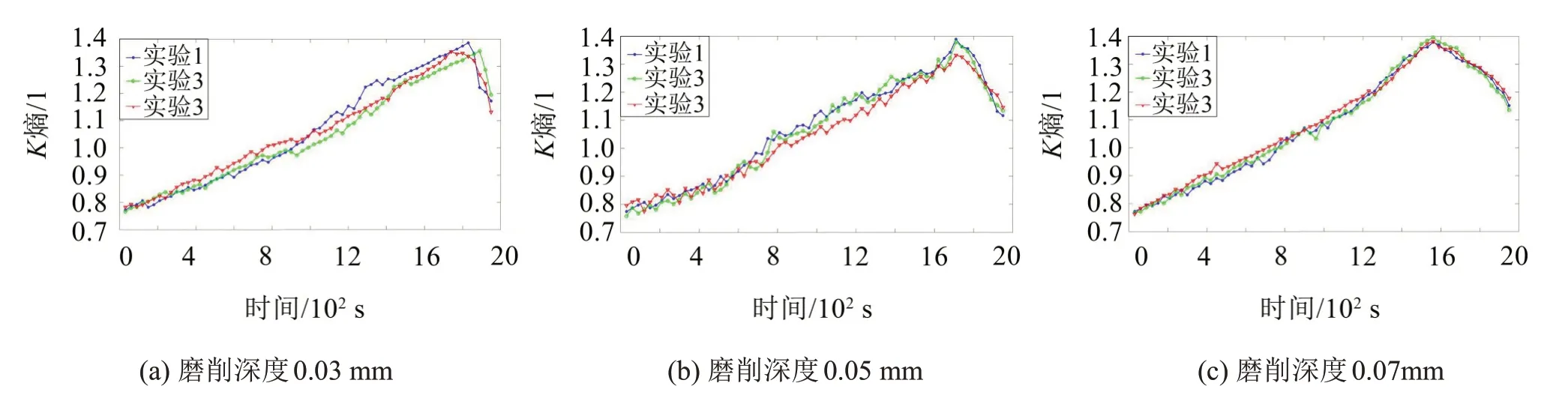
图10 不同磨削深度下的K熵变化趋势

从磨削机理来看，在初期磨损阶段，刚经过修整的砂轮，其表面的磨粒大量锐角磨粒参与磨削，这些磨粒在磨削力的作用下快速崩碎，这个阶段的声发射活动性开始增长，最大Lyapunov 指数、关联维数和K熵也开始增大。在稳定磨损阶段，磨粒开始进行正常磨削，此阶段的声发射活动性持续增强，并且蕴含着丰富的声发射信号，最大Lyapunov 指数、关联维数和K熵也持续增大。在砂轮严重磨损阶段，随着磨削加工时间的逐渐增加，磨削力急速增加导致磨削温度迅速升高，使得砂轮表面的磨粒大量断裂和脱落，造成砂轮堵塞，声发射活动性逐渐减弱，所以最大Lyapunov 指数、关联维数和K熵值都呈现下降趋势。

5 结语

（1）经过实验并计算得到，砂轮在不同磨损阶段的声发射信号最大Lyapunov 指数和K熵值都为正值，说明砂轮磨钝过程所有磨损阶段均存在混沌特性。且砂轮磨损程度越严重，对应的最大Lyapunov指数越大。

（2）通过比较不同磨削深度下的最大Lyapunov指数、关联维数和K熵值，发现磨削深度的变化对三种特征量的影响很小。

（3）利用混沌时间序列的分析方法计算得到砂轮磨钝过程各个阶段的声发射信号的最大Lyapunov指数、关联维数和K熵值，结果表明，三者的变化趋势一致，并且其变化趋势与砂轮磨损过程存在一定的对应关系。砂轮在初期磨损阶段和稳定磨损阶段，最大Lyapunov 指数、关联维数和K熵呈现逐渐递增的趋势，混沌特性增强，复杂程度越来越高；而在砂轮严重磨损阶段，三者都呈现逐渐递减的趋势，此时混沌特性也相应降低。因此，可将最大Lyapunov指数、关联维数和Kolmogorov熵作为表征砂轮的不同磨损阶段的特征量，用于描述磨钝过程中磨损的严重程度。通过这三种混沌特征量的研究，揭示砂轮磨钝过程中的动力学特性，为运用声发射信号实现砂轮磨钝过程中不同磨损程度的检测提供了一种新的思路。