遗传算法用于公交调度问题的研究

朱良学

（酒泉职业技术学院，甘肃 酒泉 735000）

公交调度[1，2]是公交企业效益的重要参照，也是衡量公交企业服务水平的一项重要指标。提升、优化公交调度水平是增强公交企业核心竞争力、提高企业效益的一项重要举措。

1 公交调度数学模型[3-5]

在加速推进城市化进程的过程中，激增的城市居住人口使城市规模渐趋庞大，城市居民的出行问题也日渐突出。过去一个简单的解决问题的做法是：适时增加线路、车辆、车次。但当城市规模达到一定程度时，结果就是带来更严重的拥堵，居民工作生活更加不便。显然，这种简单落后的管理理念和经营模式已无法满足现代城市交通新环境的现实需求，当然也无法实现乘客和公司的利益目标。

人工智能为公交车辆运营调度提供了一种新思路：对问题建立优化数学模型，利用智能算法对问题解空间进行高效搜索，在有效时间内找到满意解,形成合理高效调度方案。通过实验证明，在解决城市公共交通问题的探索过程中，这种思路是很有效的。

所谓高效的公交车辆调度,通俗的说，就是在一定的约束条件下, 在一条运营线路上，怎样合理安排车辆资源、运营时间及运行次序, 从而使线路的运营效率（减低运输成本，优化作业时间）提高，也使得乘客和公司的双方权益得到保证。

而在现实情况下，公交公司希望在发车时间段尽可能少发车次，增大发车时间间隔，提高每一车次车辆满座率，以期减少运营成本，使收益最大化；乘客则希望等车时间尽可能短一点，发车更快捷。显然利益诉求的不同导致了这一矛盾，解决矛盾的方法在于找到公交公司与乘客都能接受的一种方案，这个方案既能保证公司的合法收益，也能使乘客满意。本文正是基于这一点，在考虑乘客与公交公司各自利益的基础上，提出了反映乘客诉求的满意度函数和保证公交公司收益的满意度函数，建立了数学模型。

2 模型建立

2.1 模型

通过简化研究对象把实际问题抽象为一个数学问题，是研究解决实际问题的一条基本思路。这里做以下简化假定：该条行车线路为单行线路，共有n 站，每天的运营时间分为k 个时段；行车车辆为同一车型，满载人数都一样；乘客上下车时间短到可以忽略不计；车辆在各站之间以正常匀速行驶，每站之间运行时间也保持正常稳定。

2.2 各站点候车乘客数分析

现在以J 城市的一条公交线路来举例。对于这个具有n 个站点的线路来说，每天的运营时间可划分为k 个时段，通过统计的手段可以获得一个所谓最正常工作日内n 个站点在k 个时段内上车人数和下车人数的典型情形，这些数据是制订车辆调度表的重要依据和基础。

经过统计，n 个站点中第i 个站点在k 个时段上车人数的分布可以应用图1 来描述，K 个时段分别t1，t2，……tK。

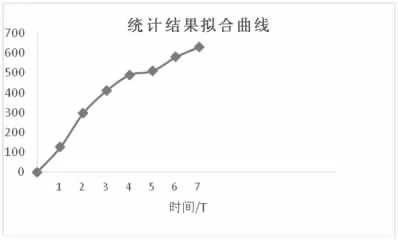
图1 站点上车人数曲线（时间）

同样的方法可以得到n 个站点中第i 个站点在k 个时段下车人数的分布。这样我们就得到了n 个站点中第i 个站点在k 个时段乘客的流量分布情形。根据统计取得的数据，将这种情形拟合成一个函数Hji(t)，并且这个函数Hji(t)是可导的，即dji(t)=H'ji(t);Hji(t)表示从每天的起始时刻到t 时刻，第j 趟车在第i 个站点达到的总乘客人数，dji(t)表示t 时刻第j 趟车在第i 站的乘客人数到站率。

2.3 公交调度中乘客的满意度函数

乘客的满意度主要考虑的因素是候车时间，假定用L 表示最长候车时间，例如在高峰时段可取值为6 min，即L=6，平时一般时段为L=10 左右等。这样，乘客人数中候车时间低于最长候车时间的人相对比较满意。采用比较简约的表示，乘客满意度可用所有乘客中候车满意人数所占的比例来描述。假定该线路n 个站点在K 个时段共发车m 趟，在t 时刻，第j 趟车到达第i 站的满意人数可以表示为：

式中，tij为第j 辆车到达第i 站的时间;t 为候车满意时间上线；在t 时刻，在第i 站，第j 趟车的乘客到站率dji(t); 在t 时刻，在第i 站，等候第j 辆车的乘客数Wij=dji（t）dt；在t 时刻，在第i 站，登上第j 辆车的乘客数Cij。这样，乘客候车满意度函数就可以如下描述：

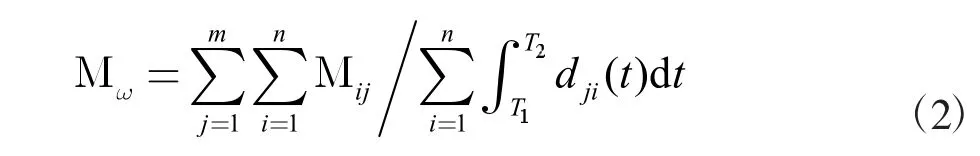
其中，总发车数用m 表示;首末班车时刻用T1、T2表示。

2.4 公交企业的满意度函数

公交线路利润=线路运营总收入-线路运营总成本，只有利润＞=某个合理值时，企业才会满意，否则企业就没有经营发展的动力。提高利润的核心显然在于提高公司的运营效率，具体反映在每天发车的数量和乘车的人数，只有发车的数量和乘车的人数达到一个均衡值，企业的效益才会最大化。从这个思路出发，先只考虑一天的情况如下：在第i 站，登上第j 辆车的乘客数Cij，线路n 个站点在K 个时段共发车m 趟，这天乘客总数即为：

3 遗传算法

遗传算法(GeneticAlgorithms，简称GA)，由J.Holland于1975 年基于自然选择和遗传原理提出。它的主要思想是：通过对问题编码，先构建一个初始种群，构成问题初始解空间；解空间中每一个个体编码就是一个染色体；根据问题实际情况设计复制、交叉和变异等算子；对解空间中每一个染色体施加复制、交叉和变异等操作，生成新的“进化”后问题解空间；用适应度函数对种群中迭代“进化”后的染色体进行选择，在此过程中，适应度值低的个体被淘汰，适应度值高的个体“延续”下来。经过这样多次对种群不断迭代“进化”，直至最终种群收敛，找到“最适应环境”的个体。这个个体即是求解问题的最优解或者满意解。显然，它是对生物在大自然中遗传进化过程的模拟，是一种具有高度并行性的随机搜索算法。

遗传算法的步骤如下。

（1） 产生初始种群。设定一个种群数，按这个数生成一定数量的遗传个体，形成初始种群，亦即解空间，它包含了所有可能的解情形。

（2） 设计适应度函数。对解空间中每个染色体个体计算其适应度函数值；以适应度函数值作为评价个体优劣的标准，优胜劣汰。

（3） 选择。淘汰适应度值低的个体，种群解空间中只留下那些适应度值较高的染色体个体。

（4） 设计变异算子。将设计的变异算子运算于染色体，产生新个体。

（5） 生成新种群。

（6） 判断是否满足问题满意条件。如果满足,执行步骤（7）；如果不满足,执行步骤（2）。

（7） 输出最优化结果。

4 禁忌搜索算法

禁忌搜索算法(TabuSearch,简称TS)是由Glover 等人于1986 年提出，其类似于模拟问题解决过程中在求解空间中摸索寻找答案的一个“爬山”过程，实现全局逐步搜索寻优。它的基本思想是：在解空间的搜索过程中，对其中已经搜索过的局部最优解。

记录下来；在后面进一步迭代搜索中，把搜索结果与局部最优解记录比较，凡是一致的，尽可能避开，这样就消除了这些局部最优解的欺骗性干扰；将搜索过程转向解空间的其他区域。如此，完成一个“爬山”过程，从而避免解空间过早收敛，即所谓“早熟”，使获得更好全局最优解的可能性大大增加。

5 用遗传算法与禁忌搜索算法结合解决公交调度问题

5.1 遗传算法与禁忌搜索算法结合

GA 的优点很显著，并行搜索能力强,有良好的全局搜索能力，能快速找出解空间中的全部解。因此比较适合求解解空间规模庞大、目标函数简洁启发性好的全局优化问题。GA 算法的局限性也很明显，局部搜索能力不好，所花费的时间成本高，特别是在迭代后期，搜索效率低，易发生早熟收敛现象。

TS 算法具有的记忆能力和设定藐视准则。由于记住了在前面搜索过程中获得的以往的局部最优解，在后续搜索时就能够跳出这些局部最优解，搜索过程中又可以接受劣解，这就极大地提高了获得更好的全局最优解的可能性。另一点是TS 弥补了GA 局部搜索能力不好的不足，因此是一种较优的全局迭代寻优算法。

因此，在解决实际问题的过程中，如果能将遗传算法与禁忌搜索算法有效结合, 这样既能保留遗传算法全局搜索能力强的优点，又能发挥禁忌算法可“爬山”、局部搜索能力好的长处，就能极大地提高在解决实际问题的过程中获得最优解的能力。具体思路是：在遗传算法进化搜索过程中,利用禁忌算法的记忆能力，构造出一个新的重组算子；再通过一个禁忌表，用来记录种群各染色体个体的适应值；在搜索过程中，这个新重组算子使用禁忌表，减少适应值较小的染色体个体出现的次数，这样就使种群尽可能保持染色体结构的多样性；通过在遗传算法中“插入”禁忌算法以提高遗传算法的“爬山”能力, 在局部搜索中用禁忌搜索算法作为遗传算法的变异算子，抑制早熟，加速收敛。

5.2 遗传算法与禁忌搜索算法结合的求解步骤

（1） 参数设定。本算法中最大迭代次数为CMax，种群规模为Zqun，交叉概率用pc表示，变异概率为pm表示。

（2） 产生初始种群。

（3） 设计适应度函数，并用适应度函数计算出当前代种群（解空间）中每个个体染色体的适应值。

（4） 选择。按照截断方式选出Zqun个染色体,放入交叉池。

（5） 交叉。具体操作如下：

①在[0，1]之间生成一个随机数ri，其中i=1，2，…Zqun；如果该生成的随机数ri≤pc，则选择交叉池中第i个染色体作为交叉的父代，产生pc×Zqun个父代染色体。

②对每对双亲运行交叉算子，产生2 个子后代。

③调用新构造出的重组算子，对交叉后得到的子后代再进行交叉操作。

（6） 变异。具体操作如下：在[ 0，1]之间生成一个随机数ri，其中i= 1，2，…，Zqun；如果ri≤pm，则调用新构造出的重组算子对交叉池中第i 个染色体运行变异操作。

（7） 产生新的种群。

（8） 如果还未达到最大迭代次数CMax，返回执行步骤（3），否则，输出最优解，算法结束。

6 实例结果及分析

J 城市该线路全线共18 个站点，线路全长10 km；线路首班车6:30 发车，末班车20:20 收车；车辆统一为普通车辆，额载24 人，最大载客数为40 人；单车成本R=17 元;单一票价为1 元。

考虑到计算量和实验条件的局限，通过测试确定参数值如下：变异概率取pm=0.01，交叉概率取pc=0.8，群体规模取Zqun=200，迭代次数取Ngen=300，禁忌表的大小为Zqun×0.6，破禁策略根据适应值确定。

表1 是遗传算法与禁忌搜索算法结合实验所得的结果。

表1 发车间隔及满意度

从实验可以看出，在所有时间段，要使两者满意度都达到最高或较高值是比较有难度的，尤其在6:30～7:00，12:00～16:30，18:00～20:20 这些时间段，还需要调整发车间隔和发车次数，以避免一方满意度较高另一方满意度极低的情况发生。

7 结论

本文构建的模型考虑了乘客和企业双方的利益，建立了乘客满意度、企业满意度目标函数。将遗传算法与禁忌搜索算法相结合，设计了新的重组算子和变异算子；通过将禁忌搜索算法作为遗传算法的变异算子，克服了传统遗传算法“过早收敛”和“爬山”能力差的缺点。从仿真实验结果可以看出，对于公交调度优化问题，通过合理设计两者满意度函数，将遗传算法和禁忌搜索算法相结合，在合理的种群规模和进化代数下，能够找到使乘客和企业双方都满意的调度方案，有效地解决公交调度优化问题。