收益法中三种折现模型的等价关系及其启示

■ 丘开浪

（厦门嘉学资产评估房地产估价有限公司，福建厦门 361016）

一、引言

在运用收益法评估企业价值中，按收益口径的不同，主要有企业自由现金流折现模型（简称：FCFF折现模型）、股权自由现金流折现模型（简称：FCFE折现模型）和经济增加值折现模型（简称：EVA折现模型）这三种折现模型。那么，这三种折现模型之间有什么内在关联？分别运用三种折现模型得出的评估结果之间有何关系？选择折现模型应注意什么问题？此外，收益法评估实务中，长期存在着一些困惑，比如：计算资本结构是采用账面价值还是评估价值？详细预测期各年的折现率是否需要动态变化？评估基准日企业的实际资本结构若与目标资本结构存在显著差异时，如何过渡至目标资本结构？计算预测首期的折现系数时，按单利还是复利计算？等等。笔者通过深入研究三种折现模型之间的本质关系，进而解答上述疑问或困惑。

二、三种折现模型等价关系的理论证明

在理论层面，通过三种折现模型间的公式推导和演算，能够证明三种折现模型等价之间相互等价。

（一）FCFF折现模型与EVA折现模型等价的推导过程① 这部分推导过程，参考了以下文献：（美）科勒，（荷）戈德哈特，（美）威赛尔斯著;高建等译.价值评估:公司价值的衡量与管理（第4版）［M］.北京：电子工业出版社，2007.2

以上是基于企业价值驱动因素公式推导出的经济增加值评估模型，其运用前提是假设公司的经济增加值未来以恒定的比率增长。推广到一般情况，经济增加值模型公式为：

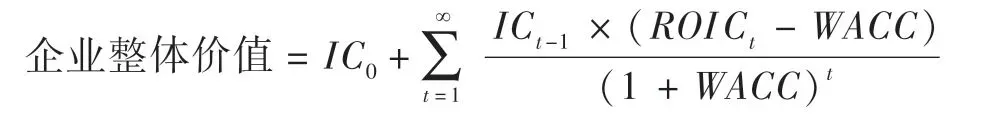
（二）FCFF折现模型与FCFE折现模型等价的推导过程

企业自由现金流（FCFF）是股权自由现金流（FCFE）与债务自由现金流（FCFC）之和。对债务自由现金流量（即税后利息费用+净偿还），以债务资本成本（Kd）进行折现，得出债务资本的价值。对FCFE，以权益资本成本（Ke）进行折现，得出股东全部权益价值。对FCFF，以加权平均资本成本（WACC）进行折现，得出企业的整体价值。企业的整体价值等于股东全部权益价值与债务资本价值之和。WACC是在Ke和Kd基础上，分别根据股东全部权益价值、债务资本价值占总资本的比例为权重计算得出的。将WACC与Ke和Kd的相互关系，与FCFF、FCFE和FCFC的相互关系相结合，FCFF折现模型和FCFE折现模型可以完全转换这一内在关联，就显而易见了。

当然，我们还可以建立相应的数学公式，推导并证明FCFF折现模型和FCFE折现模型的等价关系。为简化推导和证明过程，采用FCFF折现模型和FCFE折现模型中的资本化公式，具体证明过程如下：

企业整体价值（OV）、股东全部权益价值（EV）和债务资本价值（D）的资本化公式分别如下：

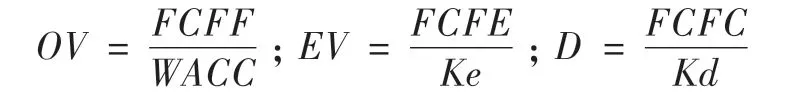
为了证明FCFF折现模型和FCFE折现模型是等价的，即证明OV-D=EV，则需要证明以下这个等式：

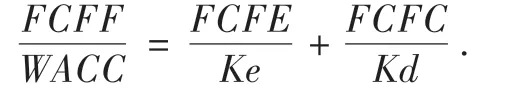
又因为

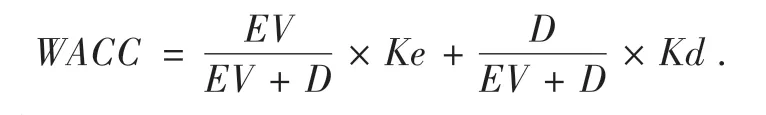
则进一步需要证明下式：

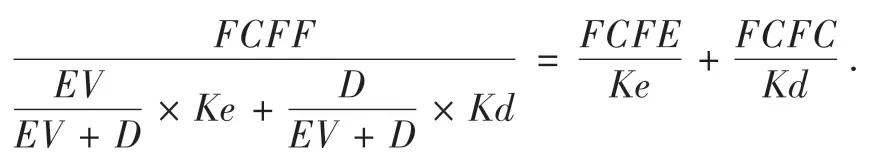
将资本化计算公式代入上式的等式左边，则：

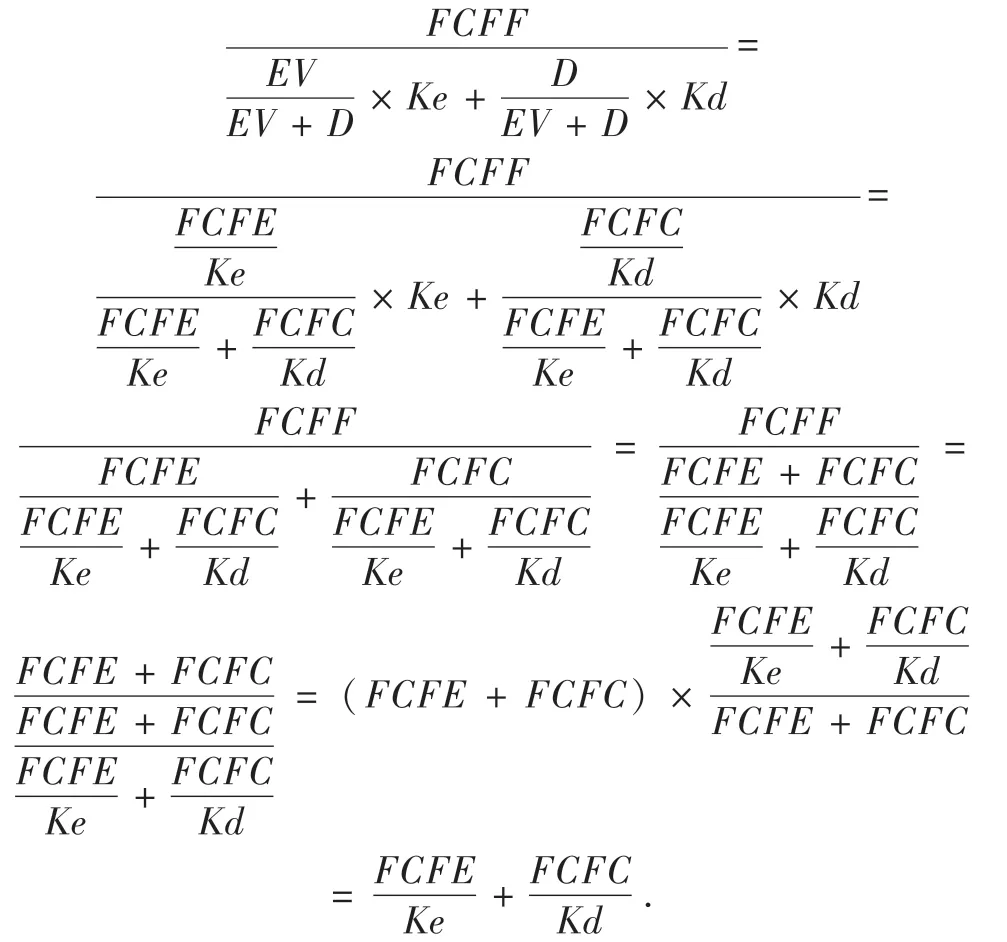
即推导出了上式的等式右边，证明了FCFF折现模型和FCFE折现模型之间的等价关系。

前述分别推导证明了FCFF折现模型与EVA折现模型等价，FCFF折现模型与FCFE折现模型等价，因而也就证明了FCFE折现模型与EVA模型等价，即这三种折现模型“两两相互等价”。

三、三种折现模型等价关系的实务运用

在理论上看，这三种折现模型“两两相互等价”可以在任何条件中适用。但在实务操作中，可能因参数取值存在缺陷或错误，表现出这三种折现模型之间并不等价。根据导致三种折现模型不等价的原因，可以将这三种折现模型不等价情形区分为两大类别：

一是因参数取值错误导致的不等价。因为参数取值的错误，使得运用这三种折现模型得出的结果并不等价。这些错误应当作出更正，对这些错误参数进行更正后，这三种折现模型仍然“两两相互等价”。

二是因参数客观缺陷导致的不等价。个别参数的取值过程存在客观缺陷，这些缺陷是非人为导致的，难以进行修复，受其制约，使得这三种折现模型之间存在不等价的情形。因参数客观缺陷导致的不等价，又有以下两项：

1.当长期增长率不为0%时，FCFF折现模型与FCFE折现模型无法等价，可能表现为FCFE折现模型的结论比FCFF折现模型的结论更高，原因在于，在FCFF折现模型中，其第二阶段的价值（即稳定期价值）的计算公式为通过该公式中的将长期增长率（g）占投入资本回报率（ROIC）之比与税后净营业利润（NOPAT）的乘积，从稳定期的现金流中扣除，作为长期增长所对应的增量追加投入，也就是说，为了维持预计的增长率，需要在企业自由现金流中扣除相应的资本性支出和营运资本净增加额。将增量追加投入的测算则与永续真实增长率相挂钩，即，永续真实增长率=投入资本回报率×再投资率。FCFF折现模型中的这种做法合理量化了企业发展所对应的“代价”，避免出现只估计永续增长不考虑增长所需投入的内在不一致情形。但是，在FCFE折现模型中，其第二阶段的价值（即稳定期价值）的计算公式为没有考虑长期增长所需要的追加投资对股权自由现金流的影响，出现了“只考虑股权自由现金流的永续增长，但未考虑所需要的增量资本投入”的内在不一致情况，这种情形下，股权自由现金流的增长相当于是“无源之水、无本之本”，这会导致评估值的虚增。

那么，为何在FCFE折现模型中不扣除永续期所需要的增量追加投入对股权自由现金流的影响呢？其根本原因在于，“投入资本”这一参数属于全投资口径指标，与FCFF的口径相匹配，但FCFE则属于权益口径，与“投入资本”的口径不一致，无法将属于全投资口径的“增量追加投入资本”从权益口径的FCFE中扣除。更进一步地看，能否将全投资口径的“增量追加投入资本”分拆出归属于权益口径的现金流金额呢？这是不现实的，“增量追加投入资本”属于资金的运用，无法像资金来源的拆分那样，将“增量追加投入资本”拆分出分别运用于权益资本和运用于债务资本的投入资本金额。因此，在FCFE折现模型中，无法恰当地将长期增长率对应的增量追加投入因素进行考量。

鉴于此，当长期增长率不为0%时，不宜选用FCFE折现模型。具体而言，当长期增长率不为0%且收益期为永续期时，应当选用FCFF折现模型或EVA折现模型；长期增长率不为0%且收益期为有限期，应当选用FCFF折现模型。

2.当收益期为有限期时，FCFF折现模型与EVA折现模型无法等价。这是因为，EVA折现模型的适用前提是，投入资本是作为“生产资料”投入企业经营并通过企业的经济增加值使这些投入资本悉数转化或收回的，但在有限期条件下，各期的投入资本在有限期内并无法全部收回或转化，还要在有限期届满时估计投入资本的剩余价值，而剩余价值的估计难以绝对准确。这也说明，当收益期为有限期时，不宜选用EVA折现模型。

在上述折现模型间不等价的两种情形中，其不等价原因，均为相关折现模型中存在不可修复的、非人为所致的缺陷因素。与其说是这三种折现模型之间存在不对价的情形，不如将其作为相关评估模型的适用条件，将存在参数缺陷的折现模型排除在适用范畴之外。即，当长期增长率不为0%时，FCFE折现模型不具有适用性；当收益期为有限期时，EVA折现模型不具有适用性。将存在参数缺陷的折现模型排除在适用范畴之外，不仅可以避免因这些存在缺陷参数的取值误差所导致的评估结论差异，而且可保持这三种折现模型也存在“两两相互等价”结论的完整性。

综上所述，可总结出“三种折现模型的相互等价关系”：当长期增长率不为0%时，不宜选用FCFE折现模型，宜同时选用FCFF折现模型和EVA折现模型；当收益期限为有限期，不宜选用EVA折现模型，宜同时选用FCFF折现模型和FCFE折现模型；当收益期为无限期且长期增长率为0%时，FCFF折现模型、FCFE折现模型和EVA折现模型均适用。在满足上述适用前提下，FCFF折现模型、FCFE折现模型和EVA折现模型之间“两两相互等价”。

四、三种折现模型等价关系的重要启示

在前面的理论分析环节，我们分别对FCFF折现模型与FCFE折现模型等价、FCFF折现模型与EVA折现模型等价进行了公式推导证明，并排除了因参数客观缺陷而影响折现模型适用性的两种情况，进而总结出“三种折现模型的相互等价关系”。在收益法的实际运用中，若运用相关折现模型得出结果之间的关系与“三种折现模型的相互等价关系”不符，则说明该收益法的运用过程有误。利用这一规律，可以基于“这三种折现模型的相互等价关系”，进一步推导得出以下结论：

（一）动态计算资本结构

资本结构反映了企业运用财务杠杆的程度，而财务杠杆是折现率的一项十分重要的解释变量，因此，资本结构是折现率的重要影响因素。资本结构对折现率的影响过程是双重的，不仅影响加权平均资本成本中的权重值，也会对权益资本成本和债务资本成本产生影响。而折现率往往是企业价值中最为敏感的指标，其微小差异可能会导致评估结果的显著差异。因此，在运用收益法评估企业价值的过程中，应当十分重视资本结构这一参数的取值。

但在实践中，在计算资本结构时，经常会出现两种错误：一是在预测期采用单一资本结构，假设各期的资本结构保持不变；二是以权益资本的账面值为基础计算资本结构。这些错误做法，没有理解资本结构的价值内涵，也忽略了资本结构在预测期动态变化的客观规律，不仅是“简单粗暴”式的“偷懒”做法，而且可能导致评估结果的错误，损害资产评估委托方或相关交易方的合法权益。因此，应十分重视资本结构的计算过程，在预测期应当对资本结构进行动态计算，具体要求如下：

（1）逐年计算资本结构。企业的资本通常包括权益资本和债务资本。在企业经营过程中，债务资本的价值通常等于其账面余额，债务资本的账面余额会随着债务的偿还或举借新的债务而发生变化；另一方面，当企业实际承担的利率水平明显偏离于客观融资成本时，债务资本的价值也不再等同于其账面余额，表现为债务资本价值的变动。因此，在预测期，企业的债务资本往往是不断变化的，当然，也可能出现债务资本不变的情形（比如，通过借新还旧的方式保持债务资本不变，且其利率合理反映了客观融资成本）。相对于债务资本，权益资本的动态特征更加显著。在预测期，企业的权益资本一定是变动的。因此，在预测期，应当逐年计算当年的债务资本和权益资本价值，逐年计算资本结构。

（2）循环迭代计算权益资本。企业价值有三大决定因素，分别是现金流、现金流的增长率以及企业面临的风险。企业面临的风险大小，又由企业所在行业的竞争特征、经营杠杆和财务杠杆所决定。企业的运作需要资本的投入，资本的投入会转化为各项资产，企业各项资产的分布以及各项资产的风险，最终构成了企业的整体风险。因此，企业的风险可以拆分为各项资产的风险，企业各项资产的风险报酬率的加权平均值，就是企业的全投资口径折现率。但是，要计算出企业各项资产的风险报酬率的加权平均值，不仅要计算出各项资产的价值，还要分别确定各项的风险报酬率，工作量和计量成本都很大。因此，实务中通常采用一种间接的途径来计算企业的全投资口径折现率，即基于资本投入的视角，计算投入资本的加权平均成本，作为企业的折现率。这种间接计量的理论依据在于，在市场均衡的作用下，企业资金运用端的各项资产的风险水平，会传导至资金来源端的各类投入资本的风险水平。比如，若企业的非流动资产（特别是非流动资产中的无形资产）占比越大，表明企业的风险越大，按照风险与收益对等的理论，则该企业的资本要求的报酬率就越高，反之亦然。因此，这种间接计量可视为是一种“等价交换”——资本投入的加权平均资本成本等于企业各项资产风险报酬率的加权平均值，而从资金来源端计算各项投入资本的加权平均成本，更加简便易行。投入资本的账面值反映了投入时点这些资本的价值，随着时间的推移及企业的运作，这些资本以及基于这些资本投入而形成的资产的价值，都会发生变化，不再等于其账面价值。因此，不论是直接计算企业各项资产报酬率的加权平均值，还是计算加权平均资本成本，均应采用当期的价值，而非历史账面价值。

因此，在计算WACC过程中，不论是权益资本还是债务资本，均应采用当期的价值。在预测期的首期中，权益资本的价值即为评估基准日被评估单位的股东全部权益价值，后者即为评估的目标所在，使得计算条件和计算结果“合二为一”，为了解决条件与目标相互重叠的问题，需建立循环关系，进行迭代计算。而对于基准日以后各年度的权益资本的价值，则应该按以下公式计算：

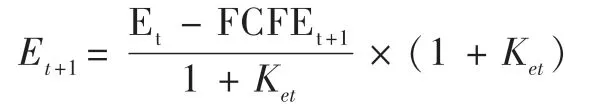
在评估实践中，还存在着将目标资本结构作为假设前提的做法，这种做法的基本步骤通常是：首先，根据可比公司的资本结构，或所在行业的相关特征及融资环境，拟定被评估单位的目标资本结构，并将该目标资本结构作为一项评估假设条件；然后，在预测期，直接采用设定的目标资本结构，或由评估基准日被评估单位的实际资本结构逐步过渡至目标资本结构。但是，基于三种折现模型的相互等价关系，按照动态计算资本结构的要求，被评估单位的目标资本结构是计算出来的，不是假设出来的。被评估单位在预测期的资本结构将如何变化，会达到怎样的水平，都是在企业未来盈利预测、资金需求、资金来源以及融资能力等因素基础上，通过动态计算得到的结果，即“先作计算，后有结果”，而不是“先假设结果，再代入计算”。因此，不宜直接假设目标资本结构，而是可以将企业在预测期的债务偿还、举借新债、股东分红或追加权益资本投入等参数的输入值，作为评估假设。

（二）滚动计算折现系数

鉴于详细预测期各年度的资本结构动态变化，各年度的权益资本回报率和加权平均资本成本是不同的，因此，在折现模型中各年度统一按照的公式计算各年度的折现系数已不再可行。相应地，预测详细期各年度折现系数应按逐年滚动方式进行计算。

（1）在FCFF折现模型和EVA折现模型中，预测期各年度折现系数按以下公式计算：

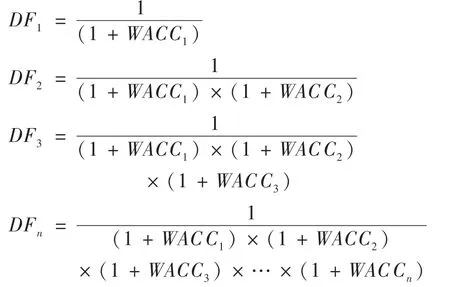
（2）在FCFE折现模型中，预测期各年度折现系数按以下公式计算：

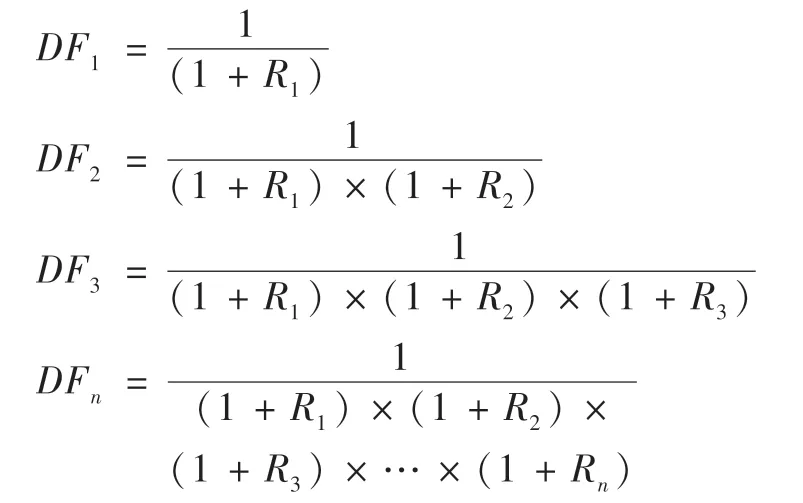
（三）预测首期的折现系数宜按单利计算

在运用收益法评估企业价值时，折现频率应与折现率对应的计息周期相匹配。当折现率为年度折现率时，因年度折现率的计息周期为一年，则折现频率为一年折现一次；当折现率为月份折现率时，因月份折现率的计息周期为一个月，则折现频率为一个月折现一次。

在运用收益法评估企业价值时，通常按年度测算折现率，每年折现一次，或每12个月折现一次。当评估基准日为非年末时，存在两种折现思路：第一种思路是，以基准日当年剩余月数为预测首期，先对预测首期进行折现，之后再逐年进行预测并折现；第二种思路是，以12个月为预测首期，此后各期也均为12个月，12个月折现一次。为简便起见，实务中通常采用第一种思路，在这种思路下，预测首期的折现系数，又有两种计算方法：

第一种计算方法，采用复利方式计算，其计算公式如下：

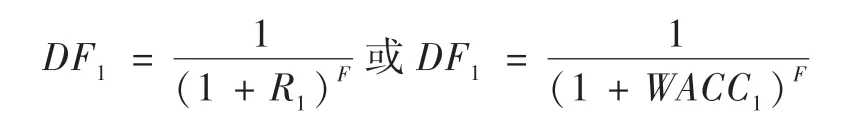
F——预测期首期的年数，即预测期首期月数除以12的值。

第二种计算方法，采用单利方式计算，其计算公式为：

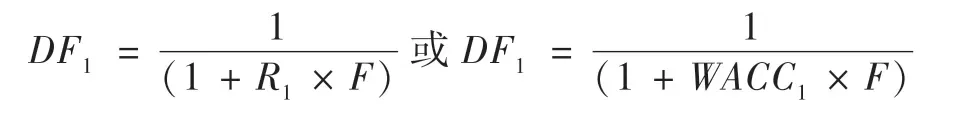
那么，预测首期的折现系数，究竟是按复利方式还是按单利方式计算呢？鉴于其折现率系年度折现率，相当于一年为一个计息周期，预测首期为非整年时，预测首期也就小于折现率对应的计息周期，此时应按单利方式计算折现系数，因为预测首期期末折现至评估基准日的时间长度小于计息周期。以基准日为6月30日为例，预测首期的时间长度为半年，但预测首期的折现率的折现周期口径仍为一年，若预测首期的折现系数按复利计算，则会出现折现率的周期口径（为一年）与预测首期的时间口径（为半年）不匹配的情形，也就是说，如果预测首期的折现系数按复利计算，则其匹配的折现率也应为“半年折现率”，且之后年份的计息周期和折现频率也要延续这一影响，即在整个收益期都要每半年折现一次，这显然与折现率通常以一年为折现周期不相匹配。预测首期的折现系数按单利方式计算时，前述的”三种折现模型的相互等价关系”成立；但若预测首期的折现系数按复利方式计算时，前述的”三种折现模型的相互等价关系”不成立。因此，基于各模型的等价关系，也可以推导得知，预测首期的折现系数宜按单利计算。

按预测期现金流的分布特征，对现金流的折现可分为年末折现和年中折现。年末折现假设各期现金流在期末发生，年中折现假设各期现金流在期中发生。在采用年中折现的方式计算折现系数时，需先确定年中折现指数。若现金流分布越偏向年末，取值越接近1；若现金流分布越偏向年初，取值越接近0；若现金流均匀分布，取值为0.5。采用年中折现方式计算折现系数，也有两种计算方法：

第一种计算方法，以复利方式考虑年中折现指数的影响，其计算公式举例（假设权益口径的折现率，假设基准日为年末）如下：

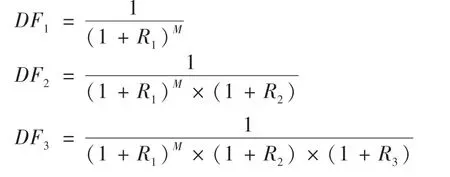
M——年中折现指数

第二种计算方法，以单利方式考虑年中折现指数的影响，其计算公式举例（假设条件同上）如下：

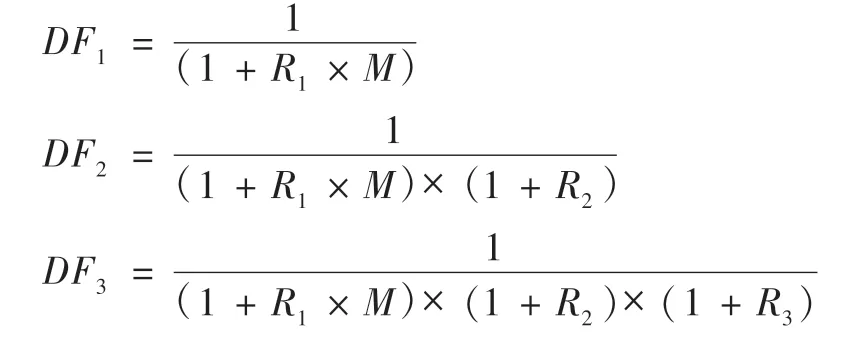
采用年中折现方式计算折现系数，相当于将各期的折现时点同步前移。比如，当评估基准日为年末、年中折现指数为0.5时，采用年中折现方式相当于将首期的折现时点前移半年，其效果也等同于将评估基准日后移半年，预测首期的折现的时间长度小于一年，也即小于折现率对应的计息周期，在计算折现系数时，应按单利方式考虑年中折现指数的影响。按单利方式考虑年中折现指数的影响时，前述的”三种折现模型的相互等价关系”成立；但若按复利方式考虑年中折现指数的影响，前述的”三种折现模型的相互等价关系”不成立。因此，基于各模型的等价关系，可以推导得知，年中折现方式下，宜按单利计算的方式考虑年中折现指数的影响。

五、研究结论

1.在理论上，通过公式推导和演算，证明了FCFF折现模型、FCFE折现模型和EVA折现模型之间“两两相互等价”。在实务中，结合运用三种折现模型的现实客观条件，可进一步论证得出以下“三种折现模型的相互等价关系”：当长期增长率不为0%时，不宜选用FCFE折现模型，但不排除可以同时选择FCFF折现模型和EVA折现模型的可能性；当收益期限为有限期，不宜选用EVA折现模型，但可以同时选择FCFF折现模型和FCFE折现模型。除此之外，FCFF折现模型、FCFE折现模型和EVA折现模型之间“两两相互等价”。

2.基于“三种折现模型的相互等价关系”及其进一步推导得出的结论，可以解决收益法评估实务中长期存在的一些困惑或争议，切实提升收益法运用的可靠性。在运用收益法评估企业价值过程中，基于“三种折现模型的相互等价关系”，至少可以得出以下三点启示：一是应动态计算资本结构，即要求逐年计算资本结构、以市场价值计算资本结构以及通过循环迭代计算权益资本价值；二是应滚动计算折现系数；三是预测首期的折现系数宜按单利计算。